培养核心素养，提高高中生数学解题能力

甘肃省文县第一中学 邹 利

高中是学生知识学习的关键阶段，数学知识内容对于学生来说存在着一定的难度，主要是因为这一学科知识内容的学习要求学生拥有良好的逻辑性思维，才能够真正理解和掌握其中所涉及的复杂知识点。同时也要求学生能够把抽象的知识转化为形象性内容，这样才能够达到课堂教学的最佳标准和要求。解题能力是学生真正了解和掌握数学知识的最主要途径之一，因此，本文也在核心素养的视角下，探析提高学生数学解题能力的方法，希望能够真正发挥出课堂教学的作用，提高学生的学习效果，为其后期的成长和进步作出贡献。

一、注重培养数学抽象素养，提升数学解题能力

高中阶段数学知识的学习具有一定的抽象性，这种抽象性主要指从数学的角度对事物之间所存在的规律进行分析得到的结果。在开展教育实践活动的过程中，学生们分析数学知识内容的形成过程，有效地提高了数学知识的抽象素养，能真正理解数学知识的本质内容，灵活地运用数学思维来解决问题。在高中阶段的数学教学里，教师从实际内容出发，运用培养学生的数学抽象思维的灵活的方法，对典型的例题进行分析，从而提高学生们的理解的能力和解答问题的水平。

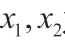
二、注重培养逻辑推理素养，提升数学解题能力

在高中阶段数学课堂教学工作中，逻辑推理能力能够帮助学生对知识进行合情推理，同时也能够演绎出推理知识内容的具体方式，学生逻辑思维能力将直接影响到学生对于数学知识的学习效果，同时也会影响到学生数学解题能力的培养以及最终所取得的成绩。在高中数学教育实践过程中，数学教师掌握了学生的理论推理能力并给予关注，而且积极地宣传理论推理的技巧和具体操作方法，要向学生传达典型事例，问题使学生们真正能够形成理论推理的经验，掌握了许多推理技巧，使学生们的数学问题解答能力相应得到提高。

三、注重培养学生转换思想，提升数学解题能力

实际上，转换法乃是对二次函数有关的实际问题加以解答的有效方法，主要通过把实际问题变成一个数学问题，之后进行解题。此种方法除了可以对问题进行简化之外，同时还能降低学生的解题难度。

比如，对于掷铅球这个问题。某校男生进行体育测试掷铅球期间，测得其出手高度是2 米，而铅球的最高点距离地面是5 米，并且距离该同学的出手点水平距离是6 米。同时已知铅球的运动路线是二次函数对应图像的一个部分，现求该同学的投掷成绩是多少米？

分析：在解答此题时，初中生应按照题意把函数图像画出来，如图所示，之后按照（6,5）和（0,2）两点把函数的表达式求出来，之后令y=0，求得的x的值便是最终答案。但此时需要考虑到实际情况，取x＞0 的值。

综上所述，纵观我国高中校园内部数学课堂教学工作实际的开展情况能够看出，长久以来，教师由于受到传统教学思想理念的影响，课堂上采取的都是应试教育的模式，很多教师为了能够提高学生的考试成绩，完全忽略了学生综合素质的培养，这也影响了其后期的成长和进步。所以在以上内容中，本文在核心素养的视角下，重点了解到高中阶段，学生数学解题能力培养的策略，希望能够发挥出课堂教学工作的有效性，使学生感受到数学知识的魅力，进而更加积极主动地参与到知识学习的过程之中，提高自己解题能力的同时，培养自己的良好学习习惯，以此为后期知识学习奠定基础。