非多重集群音程循环算法与有限移位模式拓展
张晨明 (周口师范学院音乐舞蹈学院)
在近百年来的音乐创作与研究中,数理化逻辑作为一种趋势,同时更多的是一种更加理性的思维方式影响着作曲家与音乐理论家的创作与分析研究。其中音程循环作为后现代音乐在音高结构方式上的一种数理化逻辑在例如:巴托克、艾夫斯等作曲家的作品中已经广为应用。在理论方面音程循环的分类以及相关运算在美国理论家爱德华·格林等当代理论家的努力下也日趋完善。
下文笔者主要以爱德华.格林对于非多重集群音程循环所描述的相关特点以及他所提出的相关运算为基础,对法国作曲家梅西安广为熟知的有限移位模式从音程循环的角度进行新的解读,并拓展新的有限移位模式并形成算法,同时在对相同有限移位模式拆分为不同非多重集群音程循环的方法与逻辑上进行创新与研究。
一、非多重集群音程循环与有限移位模式的同构关系
在美国理论家爱德华.格林的最近研究中,其将混合音程循环分为多重集群循环与非多重集群循环两种,爱德华格林定义多重集群循环,是指那些“以多音程混合循环的音程组,在循环的过程中所产生的多次回归原始循环点,并最终以原始音程循环组值到达起始点的现象。”①例如以Ord.PCI(2,2,1)与(1,2,2)或(2,1,2)②所构成的循环(其中Ord.PCI代表有序音级音程,括号内用逗号隔开的数字则代表音程循环的组成值)见图1。图1中笔者以方括、尖头括与椭圆分别圈出了三种用数字音级表示的循环集群。因此它们都是多重集群循环。
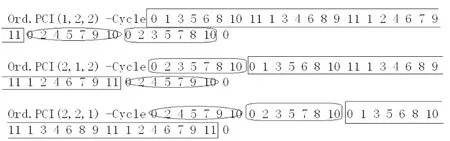
图1 (2,2,1)与(1,2,2)或(2,1,2)多重集群循环
那么非多重集群循环则是指只包含一次回归原始循环点便可以以原始音程循环组值来完成的现象。例如:Ord.PCI(2)这个以全音为循环值的单音程循环组成了全音阶,其所有组成音用数字音级来表示的话就是“0 2 4 6 8 10 0”其后续再循环下去还是“0 2 4 6 8 10 0”。又例如:Ord.PCI(2,1,1)就是“0 2 3 4 6 7 8 10 11 0”其后续循环下去也是“0 2 3 4 6 7 8 10 11 0”
经过笔者实验验证,单音程循环都符合非多重集群循环的特点,而混合音程循环则要符合其循环组成值的总和不能与12互为质数,同时计算求得的总音数不能大于12的特点才能符合非多重集群循环的特点。笔者在《浅谈爱德华格林音程循环参数算法理论》一文中指出“所有的非多重集群循环也符合在单音程循环基础上进行复合拆分的逻辑。”③那么在以模12④为逻辑的数字音级计算情况下,我们只需要考虑的单音程级只有1到6,因为其与12的补集具有与原音程级同样的特性。那么在1到6的音程级中只要是能被12整除的便都可以在其基础上进行混合音程的拆分,从而形成非多重集群循环。那么这里面只有5是不行的,同时音程级1由于无法进一步细分,因此也无法拆分成新的混合音程循环。那么当然如果一个混合音程循环的总音数大于12那么便肯定会在形成重复的数字音级的情况下产生多重集群循环,因为重复的数字音级会在循环回到起始点后打乱原始的循环组值。
那么具有这样特点的混合音程循环所构成的音阶便具有1、无法穷尽12个半音,2、其循环组值的总和与12不为质数关系,也就是说依据格林对于循环组值总和SUM与12的最大公约数GCD可以用来表示其调式移位的数量逻辑上看⑤,其仅包含有限的调式移位可能。那么这与法国作曲梅西安所提出的有限移位模式的音阶逻辑相吻合。在杨立青《真诚高雅纯挚——梅西安的音乐语言》一书中指出“梅西安的有限移位模式是将一个八度用相同的音程划分为若干相等的等分构成的,具有多次循环的同一结构细胞,它们移位可能性是有限的。”⑥那么通过验证笔者得出梅西安现有的有限移位模式都符合非多重集群循环的特性。
二、非多重集群音程循环与有限移位模式的算法及其拓展
(一)有限移位模式转换为音程循环算法模式的表述
以下有限移位模式中有关移位调式仅列出以C音(0)开始的形式,并在模12的前提下以1-11的数字音级来表示。
模式1 全音阶Ord.PCI(2) 0 2 4 6 8 10 0
模式2 八声音阶Ord.PCI(1,2) 0 1 3 4 6 7 9 10 0
模式3 Ord.PCI(2,1,1) 0 2 3 4 6 7 8 10 11 0
模式4 Ord.PCI(1,1,3,1) 0 1 2 5 6 7 8 11 0
模式5 Ord.PCI(1,4,1) 0 1 5 6 7 11 0
模式6 Ord.PCI(2,2,1,1) 0 2 4 5 6 8 10 11 0
模式7 Ord.PCI(1,1,1,2,1) 0 1 2 3 5 6 7 8 9 11 0
至此我们便得到了把梅西的有限移位模式转换归为非多重集群循环模式的七种新的表述,因此梅西安的七种有限移位模式便可以以格林的音程循环模式的算法进行研究。
(二)爱德华·格林最大公约数值对于梅西安有限移位调式移位次数的计算
爱德华指出例如以(4,5)为组值的混合音程循环,同时其GCD(12,9)=3便可以发现该循环仅有三种不同的移位形式。该循环构成八声音阶,即梅西安有限移位调式移位次数的量值。
经笔者验证该算法同样适用于所有梅西安有限移位调式的计算。如以梅西安第四有限移位调式调式Ord.PCI循环为1,1,3,1。则SUM=6,GCD=6,所以该有限移位调式包含6次有限移位。
(三)非多重集群音程循环视角生成新的有限移位模式
首先笔者依据爱德华简化混合音程循环的理论列出所有有限移位模式音程组合值的总和即SUM
模式1 全音阶Ord.PCI(2)SUM=2
模式2 八声音阶Ord.PCI(1,2)SUM=3
模式3 Ord.PCI(2,1,1)SUM=4
模式4 Ord.PCI(1,1,3,1)SUM=6
模式5 Ord.PCI(1,4,1)SUM=6
模式6 Ord.PCI(2,2,1,1)SUM=6
模式7 Ord.PCI(1,1,1,2,1)SUM=6
这样便可发现若以以上SUM值为Ord.PCI构成循环,即简化后的所有循环都是单音程循环,且无法穷尽12个半音,同时也与12为非互质关系,这也符合上文笔者对于非多重集群循环特点的论述,在Ord.PCI1、5、7、11不能被拆分的情况下,当然Ord.PCI 2也无法再拆分,那么我们便可拆分Ord.PCI(3)、Ord.PCI(4)、Ord.PCI(6)这些单音程为新的组合逻辑来构成新的有限移位模式。
在拆分之前需要解决在梅西安有限移位调式中所构成的循环中Ord.PCI的出现顺序的问题,以爱德华的理论与实验中指出的音程循环中Ord.PCI无论怎么移动都不会改变结果的原理。经笔者检验该理论对于仅有两种互异的有序音级音程有效,在拆分有序音级音程6时便会出现1+2+3这种具有3个互异有序音级音程元素的情况,那么在循环空间中这种三个互异性元素的排列便仅有2组形式如图2,向左半球的三个箭头所划分的三组数字为同一种形式1+3+2、3+2+1、2+1+3;向右半球的三个箭头划分了另外一种形式即1+2+3、2+3+1、3+1+2。因此对于三个互异有序音级音程元素的循环仅有两组排列形式。
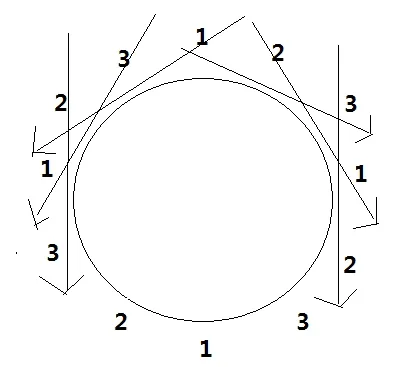
图2
至此,我们便可以开始用音程循环的方式生成新的有限移位模式了,在拆分Ord.PCI(3)、Ord.PCI(4)、Ord.PCI(6)这些单音程为新的组合逻辑时3只能拆分成1+2,因此在只有音程数4与音程数6可以拆分,即4可拆为1+3、1+1+2;6可以拆分为1+5、1+4+1、1+3+1+1、1+3+2、1+2+1+1+1、1+2+2+1、2+4;因而比较梅西安的其中模式,可再推导出5种模式,即1+3、1+5、1+3+2、1+2+3、2+4。我们以1+5为例,则SUM6首先非互质,且小于等于6,其次经计算GCD=6 L=4则该模式包含6个有限移位,音数为4如下:
(1,5)-Cycle 0 1 6 7 0因此这便是一种新的有限移位调式模式6次移位,音数4这样的新的有限移位模式还包括:
六声音阶Ord.PCI(1,3)-Cycle SUM=4 d=4 L=6,四次移位,音数6;
Ord.PCI(1,2,3)-Cycle 0 1 3 6 7 9 0 SUM=6 d=6 L=6,六次移位,音数6;
Ord.PCI(1,3,2)-cycle 0 1 4 6 7 10 0 SUM=6 d=6 L=6,六次移位,音数6;
Ord.PCI(1,5)-Cycle 0 1 6 7 0 SUM=6 d=6 L=4,6次移位,音数4。
至此便生成了另外5种有限移位模式。
结 语
通过以音程循环中非多重集群循环这一视角对有限移位模式进行解读,在对非多重集群音程循环与梅西安有限移位模式的共性上可以得出有限移位模式所组成的音阶是非多重集群循环的一种,同时非多重集群循环还包含所有的单音程循环,但在混合音程循环中其仅只有与12为非互质关系的循环组成总值成立的情况下才能实现,同时这样的混合音程循环无法穷尽12个半音,诸多特点与有限移位模式也相符合,同时在拆分Ord.PCI(4)、Ord.PCI(6)的过程中得到了5种新的符合有限移位模式的组合,并可应用算法对其相关参数进行运算。
注释:
① 张晨明.浅谈爱德华格林音程循环参数算法理论[J].音乐生活, 2019,(09).
② 同①
③ 同①
④ 罗伊格.弗朗科利著,杜晓十,檀革胜译.理解后调性音乐[M].人民音乐出版社,2012:72-73.
⑤ 同①
⑥ 杨立青.真诚高雅纯挚——梅西安的音乐语言[M].人民音乐出版社,2010:26.

