高速公路入口匝道合流区的CP-CS融合模型
温惠英 吴嘉彬 漆巍巍† 吴丽莎 张克雄
(1.华南理工大学 土木与交通学院,广东 广州 510640;2.广东省交通运输厅 水运管理处,广东 广州 510101)
入口匝道作为高速公路路网的关键节点,在高速公路系统中起着至关重要的作用,是保证入口与主线交通流不间断运行的重要过渡区。由于加速车道车辆的驾驶员必须在加速车道内完成强制换道操作,故高速公路入口匝道合流区内的交通行为更加复杂,其交通冲突频率与严重程度明显高于其他区域[1- 2]。据统计,我国高速公路合流区引发的交通事故约占事故总数的30%,其中入口匝道区域的安全问题更为突出[3]。这主要是因为入口匝道合流区的换道行为属于强制性换道,驾驶员心理相对紧张,且主线车流提供的间隙较小,导致合流区域车流拥堵,易诱发交通事故[4]。因此,合流区更容易发生交通冲突与碰撞,其安全评估更加值得重视。
目前,学者们提出了多种安全评估方法,主要分为两类:基于交通事故统计的直接评估方法和基于交通冲突分析的间接评估方法。直接评估方法主要包括回归建模[5]、灰色评价[6]以及经验建模[7]等方法,主要通过分析事故数量与频率等数据来评估其安全性。此类方法应用直接、简单,但具有统计数据质量要求严格、评估周期过长以及输出结果有限等缺点,且忽略了匝道几何设计、冲突概率与严重程度对事故的影响,导致其在实际应用中的评估效率较低。相对而言,基于交通冲突分析的间接评估方法更广泛应用于交通安全分析,主要研究可分为4类方法:模糊聚类[8]、系统分析[9- 10]、交通仿真[11]与交通冲突数据统计[12- 14]。此类方法精确度较高,模型稳定、灵活,评估指标多元化,但较少考虑车辆的实际尺寸,且过于依赖现场数据以生成多种冲突指标,如距离碰撞时间TTC、后侵入时间PET、制动时间等[15- 19]。此外,以往多数研究只能评估现有匝道的安全性,而难以对处于设计阶段的匝道建设或优化方案进行安全评估。而且同时关注冲突概率(CP)与冲突严重性(CS)对安全评估的影响的研究较少。事实上,冲突概率与冲突严重程度分别在不同维度表征碰撞风险,均对匝道安全评估效果具有显著的影响。因此,综合冲突概率与冲突严重性以评估合流区安全性具有重要的现实意义[20]。
为有效地评估高速公路现有或预建入口匝道合流区的交通安全性,文中提出了一种综合考虑冲突概率与冲突严重性的CP-CS融合模型,通过仿真实验验证该模型的有效性,并结合案例研究揭示合流区风险系数演变机理,明确不同优化方案下合流区的安全状态。
1 合流区建系
1.1 栅格划分
如图1所示,以主干道与匝道交汇点为坐标原点,构建二维笛卡尔平面坐标系,其中车流行进方向为X轴的正方向,主干路车流行进方向的左侧为Y轴的正方向。假设合流区长度为S,主干道车道宽度为D,则将合流区冲突区域均匀划分为m×n个栅格,即
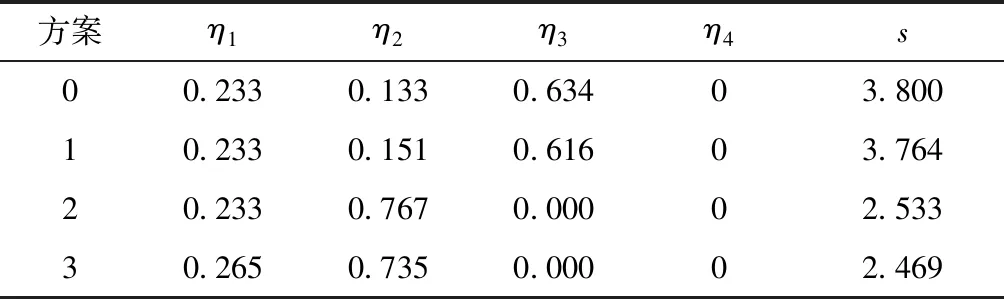
0=x0<… (1) 0=y0<… (2) 式中:i=1,2,…,m;j=1,2,…,n;m、n均为正整数,其值必须使得每一个栅格的长度与宽度均小于车辆宽度,以反映车辆到达。此时,车辆占据某一栅格任意部分均视为车辆到达该栅格单元。 图1 合流区冲突区域的坐标系与栅格划分 Fig.1 Coordinate system and grid division of conflict region in merging area 将第i行第j列的栅格记为Rec(i,j),令(xij,yij)表示栅格Rec(i,j)的形心坐标,则将车辆占据该栅格单元的概率近似视为车辆出现在栅格形心的概率,即 (3) 文中以主线双向6车道、入口匝道单车道的合流区为例,同时也可应用于其他几何形状与车道宽度的入口匝道合流区。基本假设如下: (1)由于近年来我国交通安全管理意识的提高,大部分高速公路合流区均设有禁止主线车辆换道的实线,故在此假设主线车辆进入合流区后禁止换道; (2)由于交通冲突引发的连续冲突效应相对复杂,故文中仅考虑合流区内部车辆的换道冲突与前后追尾冲突,因上次冲突引发的连续冲突不在本研究范围内; (3)假设车辆遭遇碰撞前仍保持匀速行驶。 文中提出的CP-CS融合模型是通过专家法对冲突概率与冲突严重性进行加权融合,本质上是由两个子模型组成,即CP模型与CS模型。CP-CS融合模型的表达式为 (4) (5) 文中对50位专家进行了量表调研,回收有效样本48份。通过统计量表得分可知,φcp=0.586,φcs=0.414,该取值与以往同类研究结果近似[20],则可采用四舍五入法,令φcp=0.6,φcs=0.4。 2.2.1 CP模型 为刻画实际交通工况,文中将交通冲突定义为两辆机动车在不采取制动措施情况下,在t时间内先后出现在某一栅格的现象,时间t为理论上不采取避让措施的PET值。实际上,车辆在感知到碰撞风险时通常会采取减速措施以避免事故发生,而文中所述冲突时间忽略了因驾驶员减速行为产生的时间延误,故采用折减后的交通冲突PET阈值作为冲突时间,即 t=ωtPET,cp (6) 式中:t为文中定义的冲突时间;ω为折减系数;tPET,cp为发生冲突的PET阈值,其取值参考文献[15]。 (1)冲突概率计算 冲突概率定义为在冲突时间t内最多有两辆车在同一栅格Rec(i,j)产生冲突的可能性,包括主线车辆与加速车道车辆之间的换道冲突、主线车辆间的追尾冲突,其表达式为 (7) (8) (9) (2)车辆到达概率模型 根据已有的研究[21- 23],文中将高速公路交通流划分为3种,并采用混合分布模型表征主线或加速车道车辆在时间t内到达栅格Rec(i,j)的概率,则有 (10) (3)横向偏移概率模型 相关研究表明,直行或曲线行驶车辆在车道保持上的偏差(车辆中心线与车道中心线之间的距离)一般遵循正态分布[24],即主线车辆的横向偏移概率为 (11) 式中:μ、σ2分别为正态分布的均值与方差,利用Matlab工具箱拟合横向偏移位置数据得到;Z1=[W,D],Z2=[D-W,W),Z3=[0,D-W);W为车辆宽度,W=fW1+(1-f)W2,f为大型车比例,W1为大型车宽度,W2为小轿车宽度。 (4)加速车道车辆汇入模型 在加速车道中,假设车辆行驶至x=l位置时出现可插入间隙tLC(l),用P(H≥tLC(l))表示车辆在x=l出现可插入间隙tLC(l)的概率,且服从M3分布模型[25]。根据已有研究的推导结果[26],加速车道上的车辆行驶至x=l位置进行换道的概率P(l)为 (12) (13) 式中:t0为可插入间隙均值;vB为匝道车辆速度;0.5L 2.2.2 CS模型 目前,相关的安全评估研究为交通冲突严重性的量化提供了几种定量计算方法,如TTC[27- 28]、PET[15]、Delta-V[29]以及动能损失[30]等。动能损失是指车辆经历碰撞前后的动能变化量,其大小能够反映车辆在冲突所受的作用力及速度损失。因此,许多研究人员认为碰撞动能损失是冲突严重性评估的可行方法[31]。由于动能损失模型研究相对成熟,文中直接引用现有的动能损失模型[20,31],并做出以下两点假设: (1)在碰撞前驾驶员未能及时采取制动行为,保持均速行驶; (2)车辆发生碰撞后合为一体,且在碰撞期间,系统内部合力远大于系统外力。 车辆在栅格Rec(i,j)经历碰撞后的平均动能损失为 (14) 式中:vA、vB分别是车辆A、B碰撞前的速度;β为碰撞角度,β=|θA-θB|,θA、θB分别为车辆A、B速度方向与X轴正向的夹角。 根据冲突频率与能量损失的统计数据[32- 33],文中将每个栅格的冲突概率与冲突严重性划分为4个风险等级:轻微冲突、一般冲突、较为严重冲突、严重冲突,利用绿色、黄色、橙色和红色表示风险等级由低到高,即1、2、3、4,见表1。 表1 风险等级划分Table 1 Risk level classification 由于不同风险等级取值范围跨度较大,尤其是冲突概率风险等级的划分对各栅格风险等级的表达相对模糊,故有必要对风险等级进行标准化,以显示各栅格的风险程度,标准化公式如下: (15) 由于文中CP-CS融合模型的最终输出结果为综合风险等级,难以通过统计实测数据进行直接验证,且已有相关学者利用统计数据对CS模型进行有效性验证,故可通过验证CP模型的有效性间接验证文中所建模型的可靠性。 文中通过路侧高清摄像头对广澳高速公路与灵山互通立交入口匝道合流区晚高峰(17:00—19:00)车流进行数据采集,共计302组。采集参数包括:合流区几何参数、车流速度、交通量、车型比例、横向偏移位置、车头时距以及车辆几何参数,其中主线为双向六车道,匝道单车道且合流区主线禁止换道。 根据合流区的几何参数及车流特性建立VISSIM仿真模型,输出轨迹文件后经由SSAM软件运行仿真冲突分析,输出结果如图2(a)所示,文中CP模型输出结果如图2(b)所示。 图2 SSAM与CP模型的输出结果对比 Fig.2 Comparison of output results between SSAM and CP model 为了进一步验证文中CP模型的有效性及可行性,随机选取合流区内的8个冲突栅格,对比文中CP模型与SSAM预测的冲突次数,结果如表2所示。由表中可知,各冲突栅格中SSAM的冲突次数与CP模型计算的冲突次数基本一致,存在部分差异是必然的,只有样本足够大才可能使SSAM的仿真结果与文中CP模型的输出结果相近。文中CP模型计算的冲突次数随着SSAM冲突次数的增大而增加,基本上呈现对应状态,冲突位置分布也基本 表2 SSAM与CP模型的冲突次数对比 Table 2 Comparison of conflict number between SSAM and CP model 坐标冲突次数SSAMCP模型坐标冲突次数SSAMCP模型(4,10)2234(7,30)4443(7,15)4543(11,35)4144(9,20)4845(4,38)3434(8,25)4644(12,40)2830 吻合。因此,文中CP模型可比较准确地识别匝道合流区车辆间的潜在交通冲突。 文中以广澳高速公路与灵山互通立交入口匝道合流区为案例研究对象,其主线晚高峰流量较大,匝道车流量相对较小,且两股车流在速度上具有明显的差异。文中基于CP-CS融合模型的输出结果综合计算合流区风险系数,并分析该入口匝道合流区不同流量与速度控制措施下的安全状况,以确定能够有效改善其安全状况的优化方案。合流区风险系数s为 (16) 流量控制与速度控制是高速公路合流区管制措施中较为常用的方法,可利用可变信息板对上游车流进行引导或车道分流等方式实现。在案例入口匝道中,分别对主线车流的流量与速度进行诱导调整,并根据输出结果进行对比分析。在加速车道车辆的流量与速度保持不变的情况下,设计3种主路车辆流量与速度控制方案,见表3。其中,方案0为原方案,方案1为仅降低主线车流速度,方案2为仅减少主线车流量,方案3为同时降低主线车流速度和主线车流量。 将表3数据输入安全评估模型,得到现状与速度控制方案的安全评价结果,如表4所示。 根据4个方案的安全评估结果可知:主线流量变化对合流区风险系数的影响较大,且主线流量的降低能够有效改善合流区的安全水平;主线车流速度变化对合流区风险系数的影响相对较小,但速度的减小对合流区安全水平同样具有一定的优化效果。因此,同时采取流量与速度控制措施的方案3比其他方案的安全水平更高。 表3 流量与速度控制方案Table 3 Flow and speed control schemes 表4 合流区现状风险系数的输出结果 Table 4 Output results of current risk coefficients in merging area 方案η1η2η3η4s00.2330.1330.63403.80010.2330.1510.61603.76420.2330.7670.00002.53330.2650.7350.00002.469 为进一步研究合流区风险系数与主线流量Q、速度v之间的内在关系,输出风险系数在不同主线流量与速度情况下的数值变化如图3所示,风险系数随主线流量、速度的增加呈现单调递增。当主线车流速度小于27 m/s时,风险系数增加的幅度不明显;当主线车流速度大于27 m/s时,风险系数显著增加,这主要是因为主线与加速车道的车流速度差较大,冲突引发的严重性等级骤增,从而引起风险系数的突变。当Q=250辆/h和Q=750辆/h时,风险系数变化存在降低或骤增的异常现象,这主要是因为文中采用了混合分布模型划分交通流状态导致的。 图3 合流区风险系数影响因素分析 Fig.3 Analysis of influencing factors of safety factor in merging area 风险系数与主线流量的关系如图4所示,由于不同到达分布模型的切换,车流纵向到达概率产生突变,进而引起冲突概率的不连续变化,使得合流区整体风险系数呈现异常现象。就整体而言,风险系数依然能够有效反映主线流量、车流速度对合流区交通安全水平的影响。由此可见,合流区主线流量对风险系数的影响尤其突出,车流速度的影响次之,为保证合流区的交通流安全运行,建议高速公路管理者尽量引导合流区主线车流速度小于27 m/s,流量低于1 000辆/h,以保证车流安全运行。 图4 风险系数与主线流量的关系(vA=25 m/s) Fig.4 Relation between risk coefficient and flow of main road(vA=25 m/s) 针对高速公路入口匝道合流区的潜在交通冲突预测问题,结合车辆微观运动特性,文中构建了车辆冲突概率预测模型,并对相关模型参数进行了标定;然后集成冲突概率与冲突严重性两个维度评估合流区的交通安全水平,利用SSAM冲突仿真软件验证模型的有效性,并结合实际案例确定了该入口匝道合流区的安全水平,同时分别输出案例合流区3种主线流量与速度控制方案的冲突情况,以明确不同优化方案对合流区交通安全水平的改善效果,进而揭示合流区整体安全系数随主线流量与速度变化的演变机理。 文中构建的CP-CS融合模型可以准确地评估入口匝道合流区的整体安全性,有助于工程师与规划人员综合评估或改善入口匝道合流区的管理与设计方案,以甄别最优方案,进而减少交通冲突的发生,提高合流区交通流运行的安全水平。
1.2 近似化处理
2 模型的建立
2.1 模型假设
2.2 CP-CS融合模型

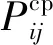
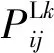

2.3 风险等级标准化


3 模型验证
3.1 参数标定
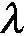
3.2 CP模型的有效性验证


4 案例分析





5 结论

