基于S变换与奇异值分解的局部放电信号去噪方法
牛海清 宋廷汉 罗新 庄小亮
(1.华南理工大学 电力学院,广东 广州 510640;2.中国南方电网超高压输电公司 广州局,广东 广州 510663)
电力设备的局部放电(PD)检测是运维人员判断设备运行状态的关键一招[1- 2]。干净的检测信号是进行信号处理的前提,但在运行现场存在白噪声的干扰,可能湮没实际的PD信号,因此研究如何有效降噪,对电力设备的状态检测具有重大的意义。
在众多的PD信号去噪方法中,小波阈值法是目前的研究热点,但其去噪效果受基小波类型、阈值选择方法[3- 6]等的影响,使用单一基小波无法同时对各种局部放电类型做有效的检测[7- 8]。近年来,S变换由于其良好的时频性,适用于非平稳信号中的高频信息提取,在地震信号处理[9]、油气识别[10]和电能质量去噪[11]方面得到了广泛的应用,但在PD信号噪声去除方面的研究相对匮乏。文献[8]通过S变换得到了PD信号的时频特征信息,表明了该方法可以很好地提取PD信号。文献[12]先采用广义S变换对特高频信号进行分析,然后采用区域最大能量法通过矩阵逆向分离将窄带干扰去除,并采用奇异值分解(SVD)抑制信号中的高斯白噪声,取得了良好的效果。

1 PD信号去噪方法的原理与流程
1.1 S变换
S变换采用Guass窗函数且窗宽与频率的倒数成正比,免去了窗函数的选择并克服了窗宽固定的缺陷[16],时间序列h(t)的连续S变换形式为
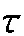
(1)
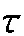
(2)
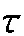
由卷积定理可得S变换的离散形式为
(3)
式中,N为采样点总数,k、n分别为时间采样点与频率采样点(k,n=0,1,…,N-1),H(m)为h(t)的快速傅里叶变换(FFT)。h(t)经过S变换的结果是一个二维复数矩阵。
根据FFT变换以及卷积定理,可以求得离散S逆变换形式:
(4)
1.2 S变换去噪原理
假设Z(t)是均值为0、方差为δ2的白噪声,Z(t)的自相关系数为[15]
E[Z(t)Z(u)]=δ2σ(t-u)
(5)
式中,t和u为时间,E表示求期望。
联合式(1)、(2)、(5),可得到白噪声Z(t)的S变换的平均功率谱[15]:
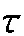
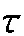
(6)
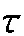
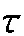
(7)
由于白噪声的平均功率谱与δ2有关,而δ2很难估计,因此文中使用SVD先判断PD信号发生的时间与个数。式(7)是一个与频率有关的线性方程,故对白噪声区域利用式(7)可求出各频率段线性方程的最大系数K。采用硬阈值法进行去噪,将K代入式(8),则绝大部分白噪声被去除。
(8)
通过硬阈值法既能去除无PD信号区域的白噪声干扰,也能去除PD信号区域非有效PD信号频率范围外的白噪声干扰。
1.3 奇异值分解去噪
SVD可以将复杂的矩阵分解成更小、更简单的几个子矩阵的相乘。根据SVD理论[17- 18],矩阵A可分解为
(9)
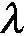
根据SVD理论可知[19- 20]:前p个较大的奇异值反映的是有效信号,后r-p个较小的奇异值反映的是噪声分量。据此可以将r-p个较小的奇异值置0,只保留前p个奇异值,经SVD重构可得到去噪后的PD信号。
奇异值有效秩阶次的选取对去噪效果的影响较大。奇异值差分谱能够有效地描述有效信号与噪声分量的奇异值差异,可实现奇异值有效秩阶次的确定[19]。令
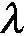
(10)
选取bi组成奇异值差分谱B=(b1,b2,…,br-1),最大峰值bp代表有效信号和噪声的分界,bp之前的p个奇异值对应的分量为有效信号,bp之后的奇异值对应的分量为噪声[19]。
1.4 局部放电信号去噪方法流程
基于S变换与SVD的PD信号去噪方法的流程图如图1所示,具体步骤如下:
1)对带噪PD信号进行S变换,得到时频矩阵。
2)对时频矩阵进行SVD,根据奇异值差分谱理论确定奇异值有效秩阶次,再对信号进行SVD重构,得到白噪声区域。
3)求出白噪声区域各频率段线性方程的最大系数K,采用硬阈值法进行去噪,再进行S逆变换即可得到第一次去噪后的PD信号。
4)返回步骤1)、2)对第一次去噪后的波形进行SVD重构,得到第二次去噪后的PD信号。
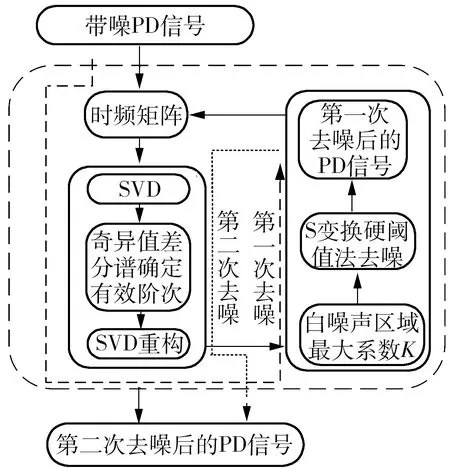
图1 基于S变换与奇异值分解的局部放电信号去噪方法的流程图
Fig.1 Flow chart of partial discharge signal denoising method based on S-transform and SVD
2 仿真信号去噪分析
2.1 PD及噪声信号模拟仿真
文献[1]指出,可以采用单指数衰减脉冲、双指数衰减脉冲、单指数衰减震荡、双指数衰减震荡模型来模拟PD信号,分别为
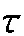
(11)
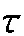
(12)
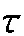
(13)
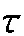
(14)
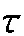
采样频率fc为100 MHz,在采样时间50 μs(采样点总数为5 000)内得到4种PD仿真信号,如图2(a)所示。对仿真信号加入方差为0.01的白噪声,得到染噪后的PD信号,如图2(b)所示。由图2(b)可见,PD信号在噪声的干扰下已无法直观地被识别。
2.2 仿真信号去噪
首先对图2(b)的带噪PD信号进行S变换,得到时频矩阵;然后对时频矩阵进行SVD。根据奇异值差分谱理论得到奇异值有效秩阶次为4。保留前4个奇异值,根据式(9)进行信号重构,得到PD信号发生的时间与个数,如图3所示。
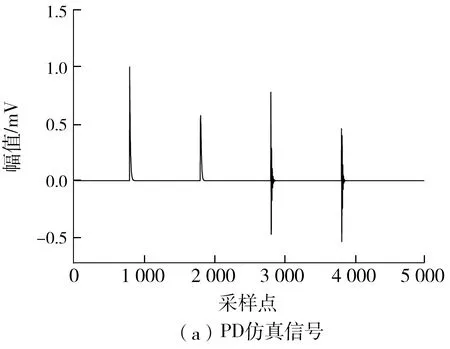
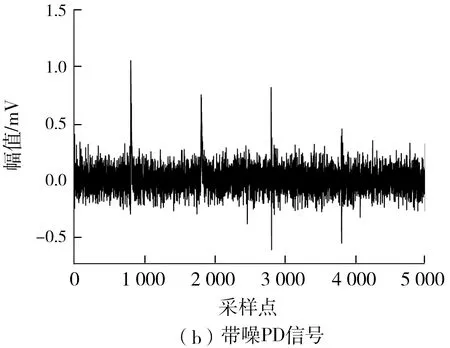
图2 有无噪声的PD仿真信号Fig.2 Simulation PD signals with or without noise
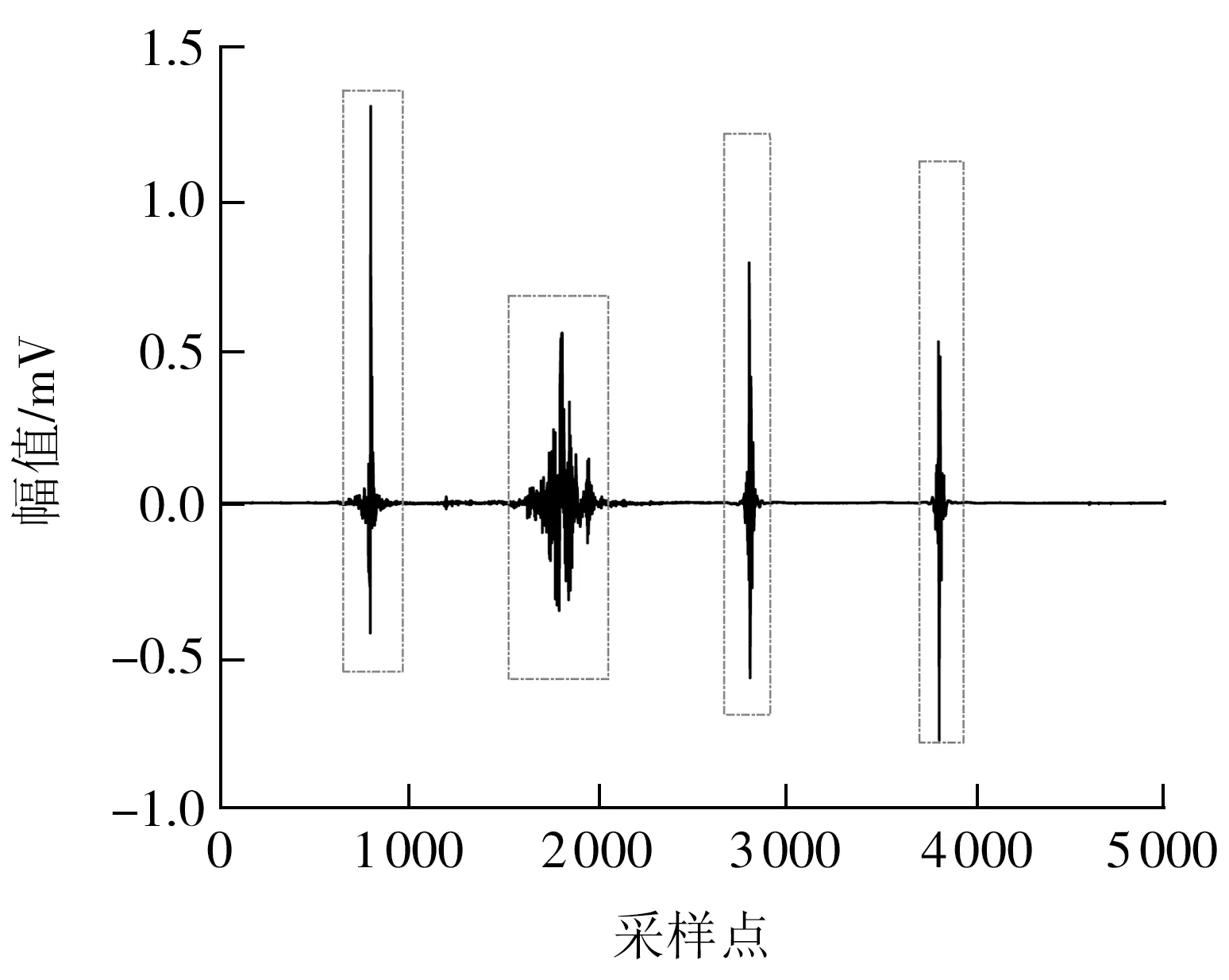
图3 重构后的PD信号Fig.3 Reconstructed PD signal
从图3可见:直接使用SVD进行去噪会在PD区域保留白噪声信号,失去PD信号原有波形特征,故第一次去噪时仅使用SVD得到PD信号发生的时间与个数;白噪声区域为[0,680]、[850,1 600]、[2 040,2 770]、[2 850,3 760]、[3 850,5 000]。
图4为PD信号第一次去噪过程示意图,斜面区域为白噪声置信区域,若信号能量小于该区域值,则认为是白噪声信号。由图4可见,绝大部分白噪声信号都被包括在内。由式(7)计算出线性方程组高频分量中的最大系数K=0.016 2,取置信区间为0.995,计算白噪声方差为0.010 4,与实际白噪声方差为0.01几乎一致,说明了文中方法的正确性。采用硬阈值法进行第一次去噪,结果如图5所示。
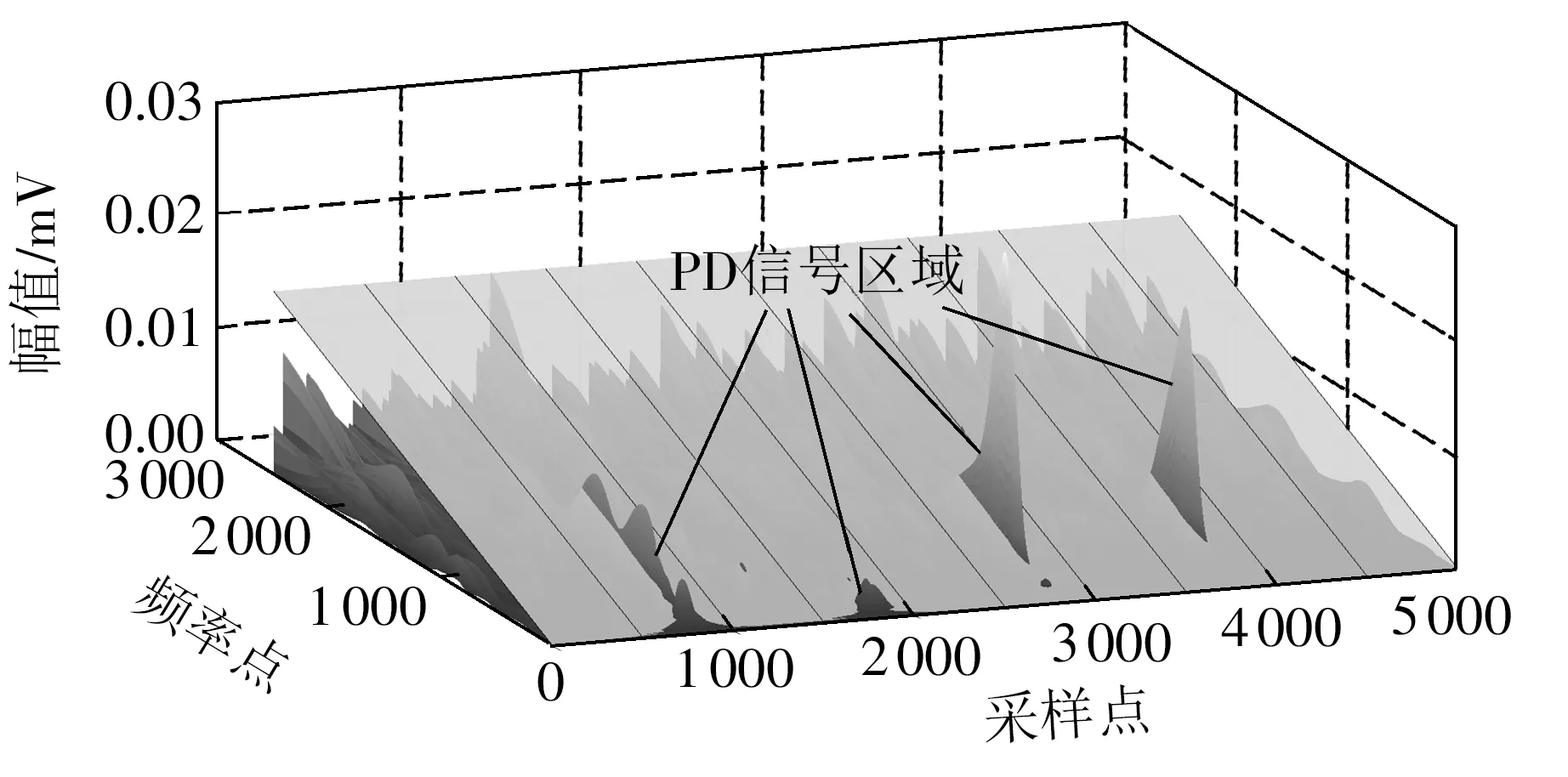
图4 第一次去噪过程示意图Fig.4 Schematic diagram of the first denoising process
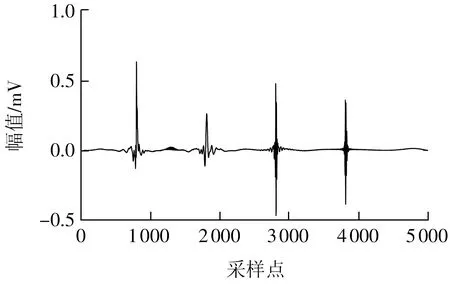
图5 第一次去噪后的PD信号Fig.5 PD signal after the first denoising
由图5和图6可见,第一次去噪时采用硬阈值法去除了部分有用信号,但仍保留了PD信号的绝大部分有用信息。由于PD信号有部分噪声未得到去除,对去噪后的波形造成了一定的影响,故需要用SVD进一步去除噪声。
经过SVD第二次去噪后的结果如图7所示。从图中可知,经过文中方法去噪后,虽然PD信号幅值有所衰减,但能够看出各PD信号的波形特征,并且PD信号区域外的白噪声已经基本去除干净。
2.3 不同方法的去噪效果对比
为验证文中方法的有效性,对PD信号进行小波分解,小波方法采用与PD信号相似度较高的sym8方法,分解层数为2,采用minimaxi阈值标准进行硬阈值处理。采用信噪比(SNR)、波形相似系数(NCC)性能评价指标对去噪效果进行评估。SNR越大,NCC越接近1,去噪效果越显著。

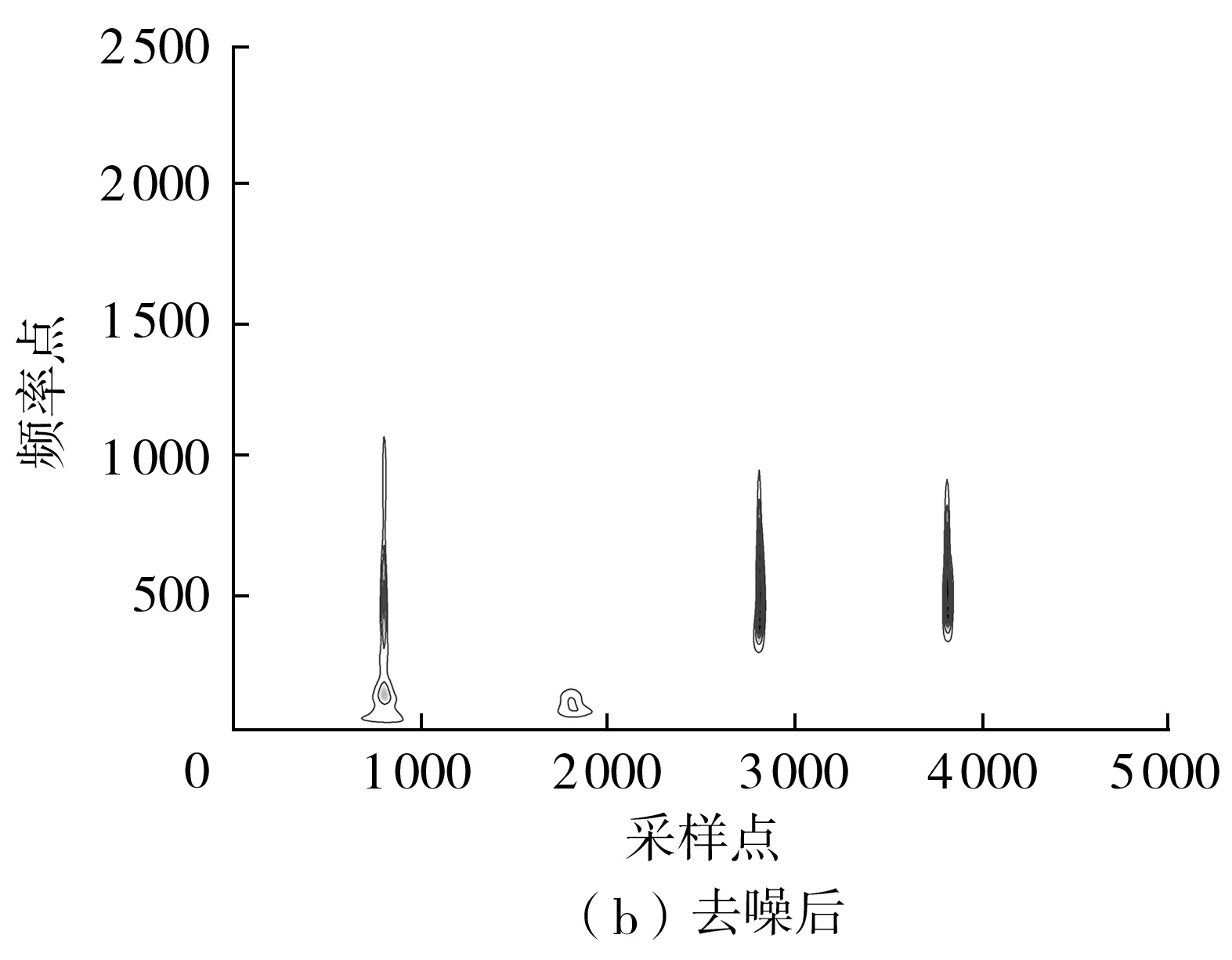
图6 去噪前后信号的S变换表面图
Fig.6 S-transform surface maps of signal before and after denoising

图7 第二次去噪后的PD信号Fig.7 PD signal after the second denoising
(15)
(16)
式中,s(k)为纯净信号,y(k)为去噪后的信号。两种方法的去噪效果如表1所示。为了消除幅值带来的影响,对PD信号幅值均进行归一化处理。
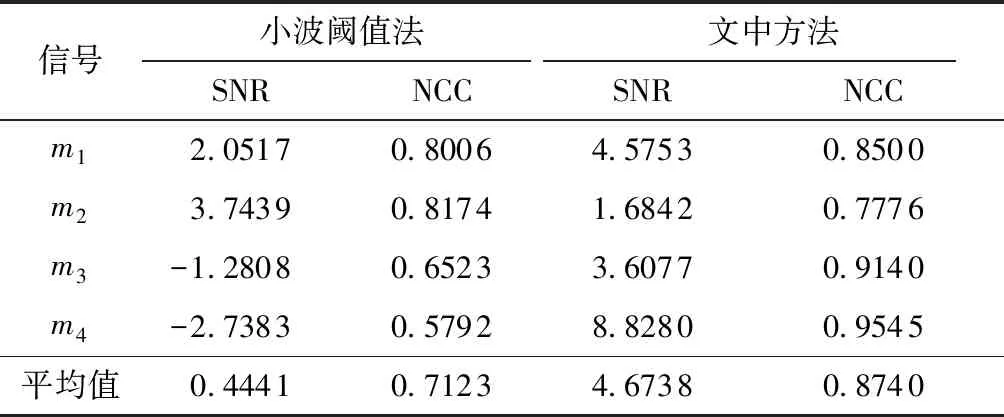
表1 两种方法的去噪效果Table 1 Denoising effect of two methods
由表1可知,无论是SNR或者NCC,文中方法的去噪效果均优于小波阈值法,尤其是对衰减震荡波信号,去噪效果尤其良好。文献[8]指出,小波阈值法的去噪效果受基小波、分解层数与阈值选取的影响,需要不断调整以达到最佳效果。相比于小波阈值法,文中方法更直接快捷。
3 实测信号去噪分析
采用HVPD公司的LongshotTM局部放电测试仪对某运行中的10 kV电缆线路进行带电PD信号检测。检测中发现某线路存在一个较强的局部放电信号,且存在白噪声干扰,如图8所示。
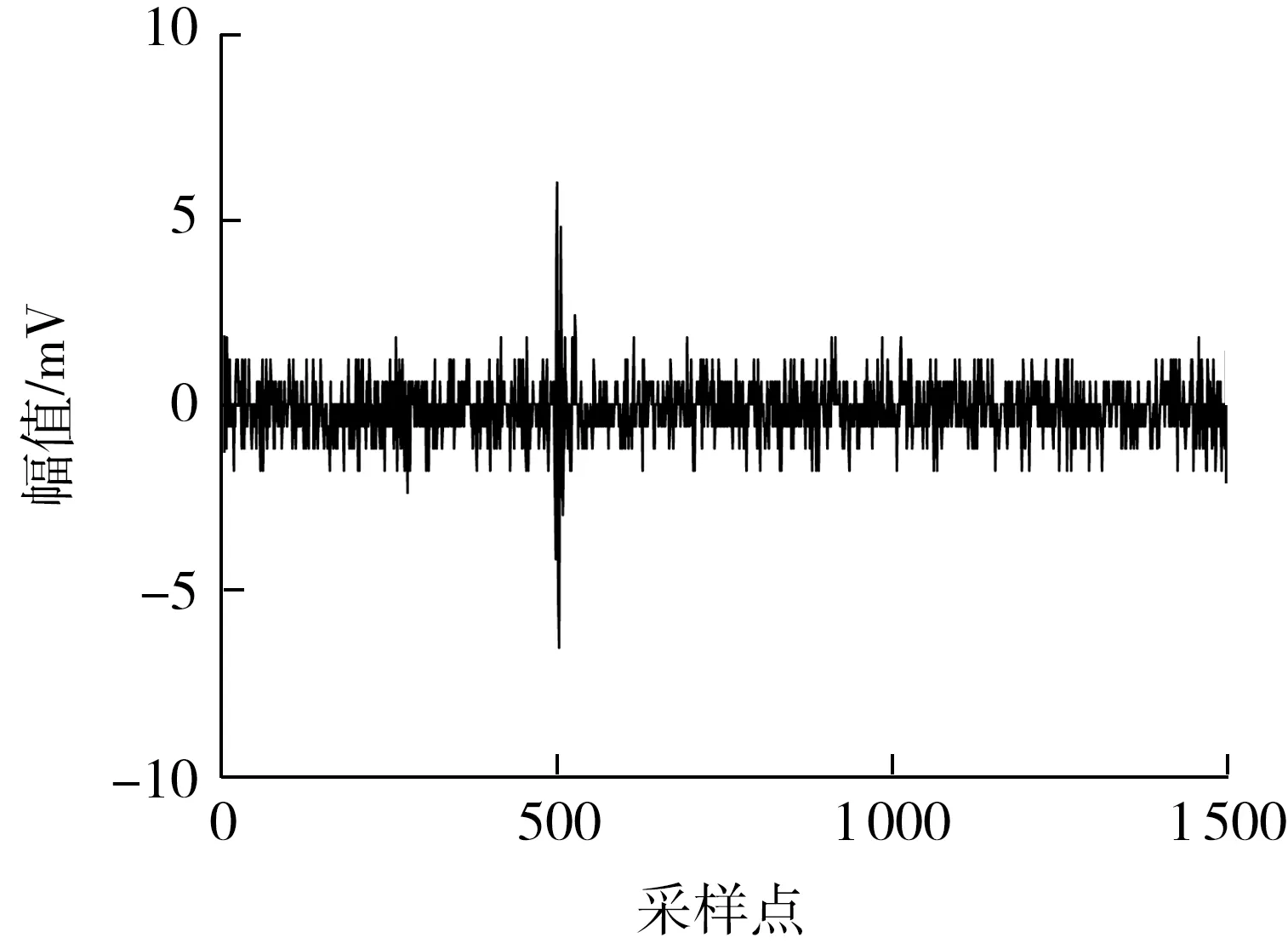
图8 带白噪声的实测PD信号Fig.8 Measured PD signal with white noise
实测信号经文中方法和小波阈值法(采用与仿真信号处理时相同的参数)去噪后的波形如图9所示。从图中可以看出,文中方法能够很好地去除白噪声干扰,小波阈值法仍保留部分白噪声干扰。此外,由于无法测到纯净的PD信号,引入噪声抑制比(NRR)对去噪效果进行定量评价[21],NRR值越大,越能凸显有效信号。
(17)

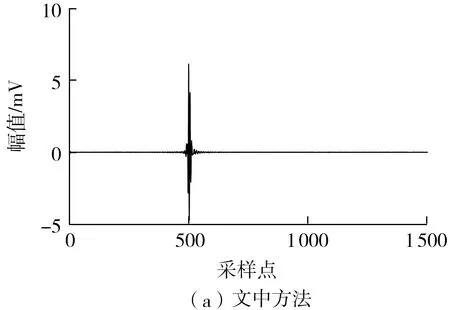

图9 两种方法的去噪结果比较Fig.9 Comparison of denoising effect of two methods
4 结论
(1)直接使用SVD进行去噪可能会使PD信号失去原有的特征,但可用于判断信号中PD信号发生的时间与个数;
(3)小波阈值法的去噪效果受基小波、分解层数与阈值选取的影响,文中方法通过S变换与奇异值分解进行去噪,方法更简便快捷,去噪效果优于小波阈值法。

