基于STEKF的锂离子动力电池SOC估算

田晟 吕清 李亚飞

(1.华南理工大学 土木与交通学院，广东 广州 510640；2.广州汽车集团股份有限公司，广东 广州 511434)

发展以纯电动汽车和插电式混合动力汽车为代表的新能源汽车，既是国际共识，也是“中国制造2025”确定的重点发展方向。我国新能源汽车的全年产销量已多年稳居全球第一，新能源汽车产业已进入高速发展阶段，与此同时也推动了以锂离子电池为代表的动力电池产业的迅猛发展[1]。精确估算动力电池的荷电状态(SOC)是动力电池系统安全稳定工作的重要保障之一。然而，动力电池结构复杂，电化学反应过程和反应阶段难以确定，而且车载环境恶劣、多变，作为隐性状态量的SOC值估算极富挑战性，一直是学术界研究的热点和行业攻关的难点。

常见的SOC估算方法有安时积分法、开路电压法、基于数据驱动的方法和基于模型的方法[2]。安时积分法存在SOC初始值难以确定且估算累积误差大的问题[2]；开路电压法需要在电池经过长时间静置后达到稳定状态才能估算SOC，不适合在车辆运行过程中使用[3- 5]；基于数据驱动的方法能较好地适应电池的非线性特征，估算精度高，但是需要电池大数据作训练，计算量较大，实现成本高[6- 7]；基于模型的方法具有实时性好、自适应强、估算精度高等特点。目前，基于电池等效电路模型与卡尔曼滤波(KF)算法及其改进算法是动力电池SOC估算中使用较多的方法[8]，其中引入多重次优渐消因子的强追踪卡尔曼滤波(STEKF)方法用于估算锂电池的SOC，正受到广泛的关注[9- 10]。

文献[11- 12]利用STEKF估算电池的SOC，但由于采用离线方式进行电池模型参数辨识，不能适应车载环境，而且验证算法的放电电流并不能如实地反映用户工况下电池的放电电流。为此，文中搭建电池的二阶RC等效电路模型，并进行模型参数的在线辨识，最后在ECE15工况下完成STEKF对动力电池SOC的估计试验，以论证该方法对车载环境的适应性。

1 锂离子电池建模与参数辨识

1.1 锂离子电池建模

图1 二阶RC等效电路模型Fig.1 Equivalent circuit model of second-order RC

系统激励为锂离子电池的工作电流i(t)，系统观测变量为工作电压U，根据Thevenin定理建立的电池状态方程为

(1)

观测方程为

U(t)=Uoc(t)-US(t)-UL(t)-i(t)R0

(2)

将状态方程和观测方程离散化并表示为矩阵形式，有

(3)

U(k)=Uoc(k)-US(k)-UL(k)-i(k)R0

(4)

式中，Sk和Sk-1分别为k和k-1采样时刻的电池SOC值。

1.2 开路电压的测量

电池的SOC(S)与开路电压(OCV，Uoc)存在一定的函数关系，文中采用开路电压快速测定法进行OCV-SOC非线性曲线的测定。在相同SOC值下，以多次脉冲充放电实验静置的最终时刻端电压均值作为该SOC对应的开路电压值，应用Matlab/cftool工具箱对多次实验得到的OCV-SOC数据组进行多项式拟合。经拟合后可知，五阶多项式的拟合精度高于四阶多项式一个数量级，而六阶多项式的拟合精度与五阶相差较小，因此，选择五阶多项式进行拟合，拟合曲线如图2所示，得到的拟合方程为

Uoc=0.293 7S5-3.715S4+6.389S3-

3.723S2+1.549S+3.307

(5)

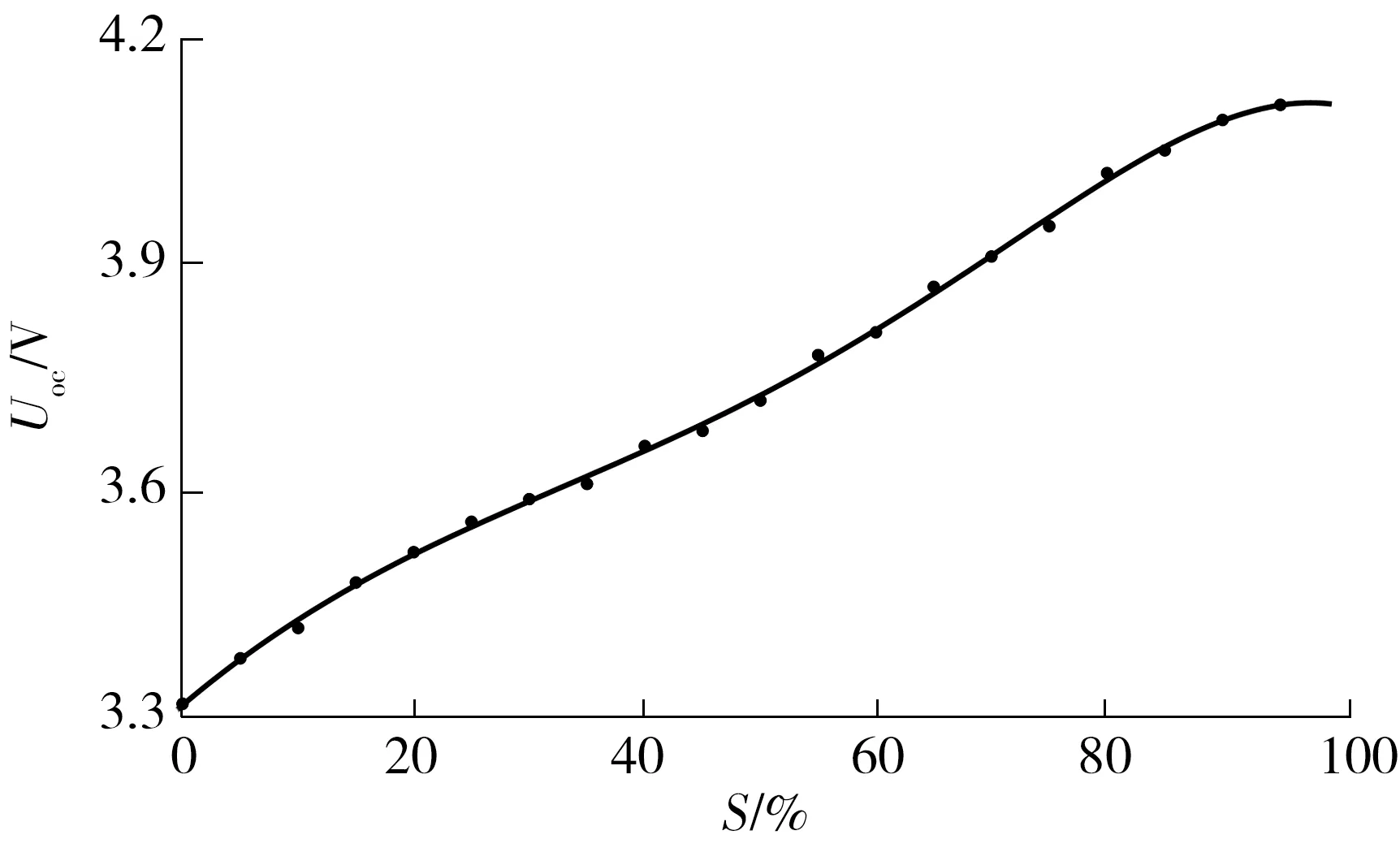
图2 电池的OCV-SOC曲线Fig.2 OCV-SOC curve of battery

1.3 模型参数辨识

电池的二阶RC等效电路模型搭建完成后，需要确定模型参数R0、RS、RL、CS、CL。由于电池的健康状态(SOH)、电流强度、温度等因素容易对电池参数产生影响，使其值发生波动。因此，为准确地描述电池的实际状态，需要对模型参数进行在线实时辨识，常用的参数辨识方法包括卡尔曼滤波、脉冲实验法和最小二乘法等。卡尔曼滤波法由于计算时间较长而不适用于参数在线辨识；脉冲实验法需要电池静置一段时间，因此，该方法不适用于车载条件下辨识参数；最小二乘法具有拟合精度较高、易于工程实现等优点，能在线辨识模型参数。

文中以最小二乘法辨识电池模型参数时，电池系统会被简化为以工作电流i(t)作为输入，电池端电压U用作输出的单输入输出系统，通过分析模型，建立系统的状态方程，然后求解方程各项未知系数，进而推导出等效电路模型的各项参数，详细的求解过程如下：

系统在频域下的状态方程可由二阶RC等效电路模型得到，即

(6)

令U′(s)=U(s)-Uoc(s)，得到传递函数

(7)

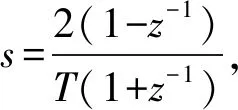
(8)

待定系数lj(j=1，2，3，4，5)为

(9)

根据式(9)求得状态方程的差分方程为

U′(k)=l1U′(k-1)+l2U′(k-2)+l3i(k)+

l4i(k-1)+l5i(k-2)

(10)

电池的荷电状态、健康状态(SOH)、温度θem都是关于时间t的函数，电池模型的开路电压Uoc与它们相关，于是可定义Uoc为

Uoc=f[θem(t),H(t),S(t)]

(11)

求导可得

(12)

式中，H为电池的SOH值。当采样时间T取较小值时，假设由于在电池温度管理系统(BTMS)的作用下，在采样时间T内，电池温度几乎未发生变化，即∂θem/∂t=0；假设在采样时间T内，电池容量未发生衰减，此时，电池健康状态几乎不变，即∂H/∂t=0；同时假设在单个采样时间T内，电池消耗或再生的电量没有改变，即∂S/∂t=0。基于上述假设，式(12)可以简化为

即

ΔUoc(i)=Uoc(k)-Uoc(k-1)=Uoc(k-1)-

Uoc(k-2)

(13)

将式(13)代入差分方程式(10)，整理可得

U(k)=(1-l1-l2)U(k)+l1U(k-1)+

l2U(k-2)+l3i(k)+l4i(k-1)+l5i(k-2)

(14)

(15)

2 基于扩展卡尔曼滤波的电池SOC估算

扩展卡尔曼滤波法(EKF)是一种高效的线性滤波和预测方法，通过当前时刻的观测值与上一时刻的估计值进行状态值的实时估计，在动力电池SOC的估算上已有广泛的应用。

设系统的状态方程为

(16)

式中，X(k)为系统的状态向量，U(k)为系统的输入量，f[X(k)，U(k)]为转换函数，w(k)为过程噪声向量，Z(k)为系统测量输出量，v(k)为系统测量噪声向量，h[X(k)，U(k)]为系统测量函数。

系统滤波的过程如下：

1)设置滤波方程的初始条件为

2)更新估计状态

Xk/k-1=f[X(k-1),U(k-1)]=AX(k-1)+

BU(k-1)+w(k)；

3)更新误差协方差

4)更新卡尔曼增益矩阵

5)更新估计状态的测量

Xk/k=Xk/k-1+Kk{Zk-g[Xk/k-1,Uk]}；

6)更新估计协方差的测量

Pk/k=[I-KkCk]Pk/k-1。

3 基于STEKF的电池SOC估算

当系统状态量处于平衡状态时，状态量保持不变，卡尔曼增益Kk会接近于0，此时系统状态若发生突变，系统残差γk将急剧增大，而Kk是无法对该变化做出及时响应的，由此会导致EKF对系统状态估算的误差骤增。电动汽车在使用过程中，由于外部环境的变化，车辆运行的工况也随之变化，导致电池端电流剧烈波动，即常常存在状态突变的情况，同时电池模型误差不可避免，因此在车辆实际工况下采用EKF估算电池的SOC的精度不高。为克服EKF的不足，文献[15]提出了一种将EKF与强追踪滤波器(STF)结合的STEKF滤波器。

STF通过使算法输出的残差序列强制以正交的形式输出，使得滤波输出具有很强的离散性，同时能够对原系统输出的残差进行二次信息提取，增强系统的鲁棒性，并使系统具有很强的追踪能力[16]。文中采用STF与EKF相结合形成的STEKF来估算电池的SOC，引入多重次优渐消因子在线优化先验状态量估算值的误差协方差阵，以增强滤波器对突变状态的响应能力，同时调整卡尔曼增益对系统旧数据进行渐消，降低新数据对旧数据的依存度，进一步提升对电池SOC的追踪能力。采用STEKF估算电池SOC值的流程图如图3所示。

图3 基于STEKF的电池SOC估算流程图Fig.3 SOC estimation flow chart of battery based on STEKF

基于STEKF的锂离子电池SOC估算步骤如下：

1)确定初始化变量k=0时的X0、P0、系统过程噪声Q、观测噪声R；

2)以第k-1步的状态量后验估计值Xk-1/k-1、协方差矩阵Pk-1/k-1估计第k步的状态先验估计值Xk/k-1，并以Xk/k-1为输入计算输出估计值Zk/k-1；

3)计算输出残差rk及相应的残差协方差阵Vk，即

rk=Zk/k-Zk/k-1，

遗忘因子ρ∈(0，1]，通常取0.95；

4)求解多重次优渐消因子

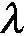
6)计算第k步的卡尔曼增益矩阵

7)计算残差rk，并结合卡尔曼增益进一步更新第k步的状态先验估计Xk/k-1，得到后验估计值；

8)计算状态后验估计值Xk/k的误差协方差阵Pk/k=[I-KkCk]Pk/k-1。

4 仿真实验及结果分析

为了验证基于STEKF的电池SOC估算方法的准确性和适用性，并与采用EKF估算电池SOC的效果进行比较，文中选用额定容量为42 Ah的某型动力电池作为测试对象，通过实验平台与Matlab/Simulink仿真软件联合进行实验验证。实验数据由电池测试平台采集，测试平台由智能充放电测试仪、电脑及监控软件组成。选用接近电动汽车实际行驶工况的ECE15工况对电池进行充放电实验，将采集的实验数据在Matlab/Simulink中进行仿真。仿真初始时选择电池SOC初始值为0.9，由于US、UL在起始阶段的极化效应不明显，故其值可近似为0。图4为ECE15工况下的电流与电压波形，图5为EKF与STEKF估算电池SOC的结果曲线及误差曲线，其中EKF和STEKF估算的电池SOC曲线由Matlab仿真得到，电池SOC实际值由测试平台得到。

从图5(a)可知：初始阶段EKF与STEKF估算的电池SOC曲线基本重合，之后电池经历电流突变和大倍率放电，EKF与STEKF的估算曲线开始分离，STEKF由于引入多重次优渐消因子，优化了卡尔曼增益，因此可保持对实际SOC较强的追踪能力；然后进入放电平稳期，EKF曲线开始向STEKF曲线和实际SOC值靠拢；最后进入放电尾期，EKF与STEKF的估算差距再次增大，但STEKF仍保持对SOC真实值较强的追踪能力。从图5(b)可以看出：STEKF可以保持对SOC真实值的较强的追踪能力，误差一直保持在2%以内；EKF在开始和中后期对真实SOC保持较好的追踪能力，但在中前期和末期由于电流突变和电池的模型误差，估算的电池SOC误差较大，最大误差为3.2%。

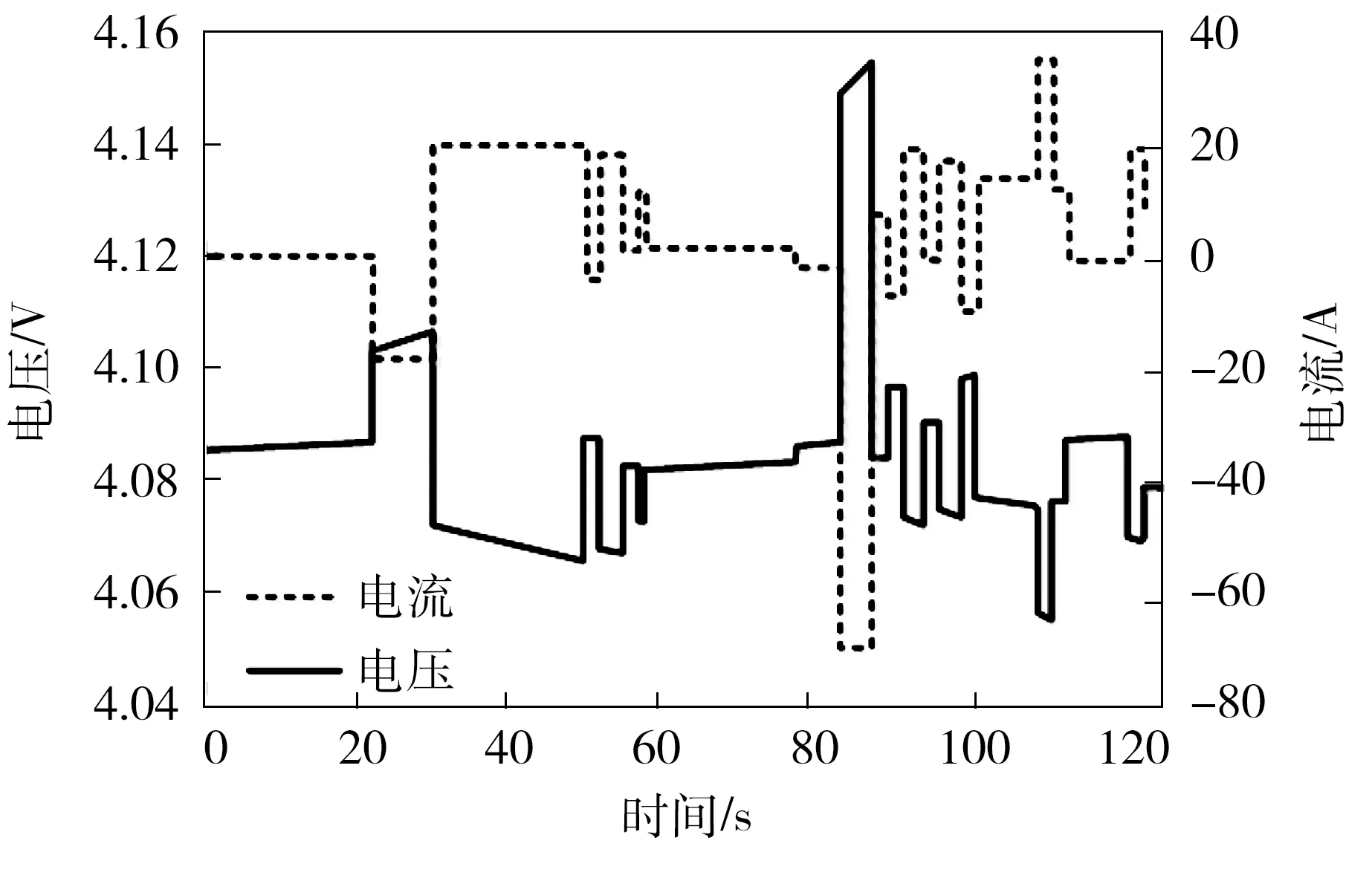
图4 ECE15工况下的电压与电流波形

Fig.4 Waveforms of voltage and current under ECE15 condition

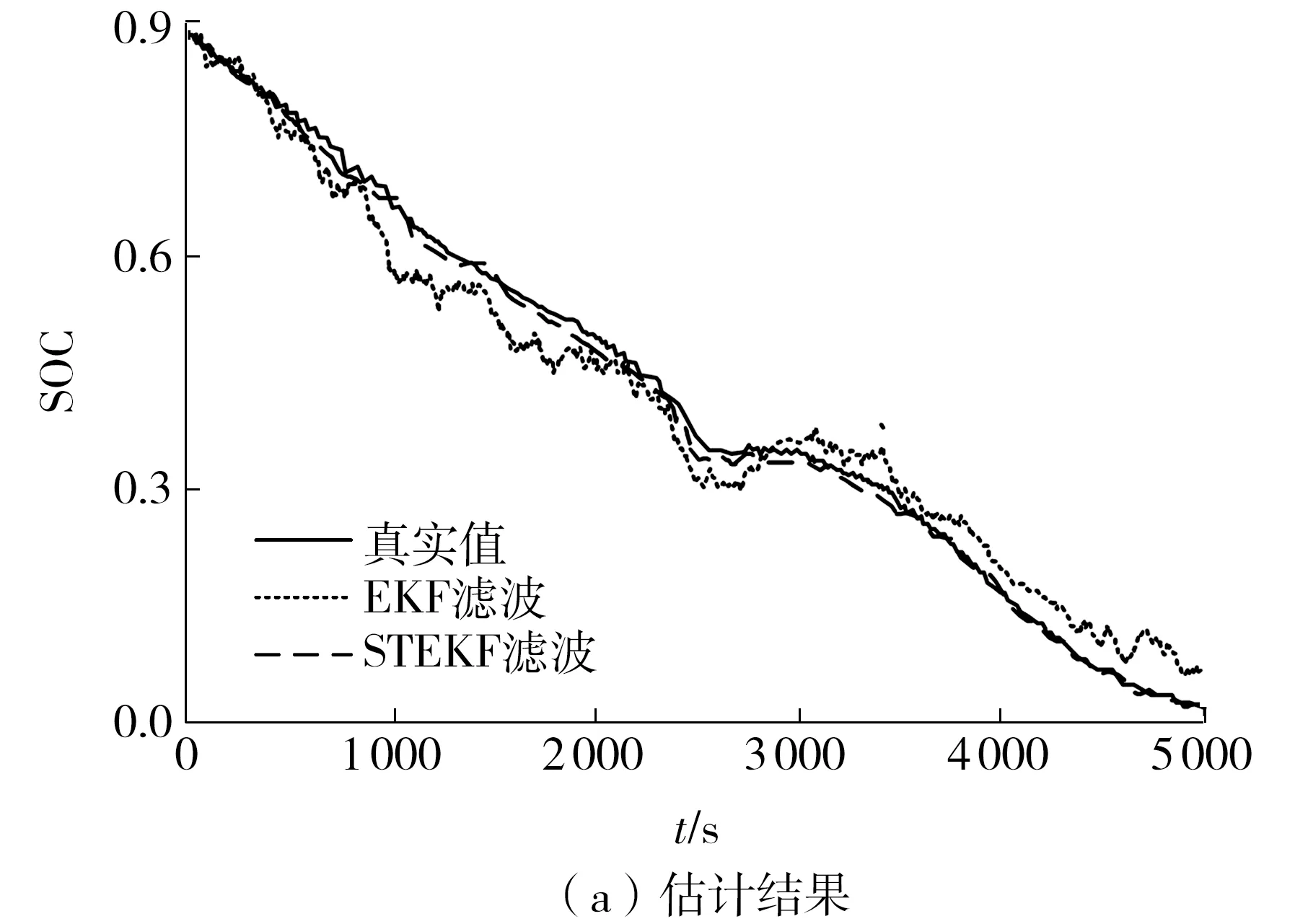
图5 EKF与STEKF估算电池SOC的曲线及误差曲线

Fig.5 SOC estimation curves and error curves of battery by EKF and STEKF

5 结语

针对复杂工况下EKF无法实时追踪电池SOC的问题，提出了一种引入多重次优渐消因子的扩展卡尔曼滤波方法STEKF，即在EKF的基础上，增加多重次优渐消因子在线优化先验状态量估算值的误差协方差矩阵，以增强滤波器对电池SOC曲线的追踪能力，最后在ECE15工况下进行仿真实验。结果表明，相较于EKF算法，引入了多重次优渐消因子的STEKF在ECE15工况下估算电池SOC的误差能保持在2%以内，取得了较好的估算效果，而且该方法能适应车载环境，在现有的电池管理系统硬件的基础上进行软件升级即可实现，可实施性强。但文中并未考虑温度和电池的健康状态对电池模型的影响，这些将在未来的工作中加以完善。