小波形波纹钢加固混凝土管涵的试验研究

李百建 朱良生 李勇 符锌砂 葛婷

(1.华南理工大学 土木与交通学院，广东 广州 510640；2.广东技术师范学院天河学院 土木工程系，广东 广州 510540；3.苏州科技大学 土木工程学院，江苏 苏州 215011)

将波纹钢管插入到既有钢筋混凝土管中，并在两者之间填充混凝土，这种方法称为内衬加固法[1]，是一种不中断交通、节省投资的加固补强方法。目前，主要有两种模型来分析加固管涵的承载力，一种是以铸铁管道为载体,基于弹性假设形成的“套管理论”[2]，另一种是以小孔径的混凝土管为载体形成的“组合理论”[3]，前者认为既有管涵、填充混凝土和内衬管是相互滑移、无粘结的，后者认为它们是完全粘结、无滑移的。然而，随着研究的深入，学者们发现“套管理论”和“复合结构理论”很可能是加固管涵的两个极端情况[4- 5]，因为不同的既有管涵不能一致地保持弹性变形，那么以铸铁管为载体形成的“套管理论”就存在缺陷;另外,既有管涵、灌浆或填充混凝土、内衬管之间无法完全粘结，这使得“组合理论”也不尽合理。与此同时，有一些研究甚至是矛盾的，如有些人认为填充混凝土对加固管的承载力没有影响[6]，而有些人则认为填充混凝土对加固管的承载力起了很大的作用[7]，还有些人认为既有管涵的腐蚀程度对结构性能没有影响，在管底铺设衬砌可以提高管涵的力学性能[8]。无论怎样，研究人员一致认为内衬确实提高了既有管涵的承载能力和刚度[9]。

尽管学者们已经对内衬加固做了一些研究，但研究深度、广度还不够，没有完全揭示出加固后管体的力学机理，也没有形成相应的设计规范，如美国规范[1]、加拿大规范[10]和中国规范等均没有相应的设计条款和承载力计算公式，只有《排水管维修手册》(Sewerage Rehabilitation Manual)[11]给出了计算加固管承载力的建议方法，但没有给出更为合理的强制性规定。

为了探索波纹钢管加固混凝土管的力学机理以及承载力的计算方法，文中采用钢筋混凝土管作为既有管涵，并采用小波形的波纹钢管对其进行加固，做了一系列试验。研究以试验为主，致力于探索加固管的承载能力，填充混凝土和小波形波纹钢对加固管的贡献，以及偏心加固对加固管承载力的影响，并针对试验结果给出了一种估算加固管承载力的方法。

1 试验设计

为研究波纹钢加固管的力学性能，试验采用了4个混凝土管(从混凝土管预制厂购买)，内外表面光滑，公称内径为1 200 mm，公称壁厚为120 mm；管壁内布置双层冷拉钢筋(φ6，HRB400)，间距为100 mm，配筋率为0.282 6%；混凝土管采用的混凝土强度等级为C45，混凝土试块的抗压强度平均值为(43.97±4.00)MPa，弹性模量为33.5 GPa。钢筋的强度等级为HRB400的冷拉钢筋，最小屈服强度为400 MPa，拉伸试验测得的极限抗拉强度为(575±9)MPa，钢筋的弹性模量为210 GPa。

波纹钢管的规格为125 mm×25 mm×3 mm，钢材牌号为Q235，最小屈服强度标准值为235 MPa，最小极限强度标准值为370 MPa，弹性模量为210 GPa，双面镀锌。每毫米长波纹钢的截面面积为3.294 mm2，惯性矩为264.107 mm4[12]。

国外通常采用水泥砂浆或者灌浆料作为内衬与混凝土之间的填充材料，国内通常采用细石混凝土作为内衬与混凝土之间的填充材料。为了与工程实践相符合，试验采用填充混凝土，其等级为C30，混凝土试块的弹性模量为30 GPa，抗压强度平均值为(30.35±2.00)MPa。

试验共使用了5个试件，包括：①一个混凝土管(RCP)；②采用波纹钢加固的混凝土管(RGC)；③先采用波纹钢加固混凝土管，然后刨掉波纹钢部分，仅剩填充混凝土和混凝土管的加固管(RG)；④采用波纹钢偏心加固的混凝土管(ERGC)；⑤一个波纹钢管(CSP)。所有管长均为1 000 mm。加载示意图如图1所示，试件如图2所示。

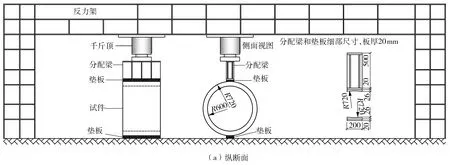
图1 加载方案示意图(单位：mm)Fig.1 Schematic diagram of the loading frame(Unit:mm)

图2 两点加载采用的试件Fig.2 Specimens used in the two-point loading setup

由于波纹钢管具有波纹，所以填充混凝土的厚度指不包含波纹的厚度，即波纹钢外表面至钢筋混凝土管内表面的厚度。RGC和RG两个试件的填充混凝土厚度为75 mm；ERGC试件的填充混凝土在管顶的厚度为150 mm、管底的厚度为0 mm(垂直偏心加固，波纹钢管与混凝土管在管底紧密接触)，参见图1。

试验采用4个位移计测量了竖向、水平位移，其中2个位移计安装在管顶、管底的内侧，因为管顶、管底外侧安装了加载垫板，并且管顶、管底变形时是紧密接触的，钢筋混凝土管、填充混凝土和波纹钢管的竖向位移相等，考虑以上原因，将位移计安装在内侧。另外2个位移计安装在管侧的外侧，因为水平变形时钢筋混凝土管、填充混凝土和波纹钢管有可能在管侧发生分离现象，钢筋混凝土管的水平位移将会大于波纹钢管，考虑最不利情况，所以将位移计安装在管侧的外侧来测量最大水平变形。此外，在波纹钢管内侧的环向八分点位置安装了应变片，分别安装在每个截面的波峰、波谷上，用来判别不同受力阶段时波纹钢截面的内力，以此推测波纹钢管的贡献作用，所有测试元件安装在试件中部位置。

为了研究波纹钢加固钢筋混凝土管涵的力学性能，试验采用了两点加载，两点加载试验的好处是管涵的内力-变形可以简单地通过力学计算得到，但缺点是不能够反映管涵的实际受力状态。虽然三点加载(管顶、管侧两边加载)是较为合理的加载方式，但由于加载设备复杂、需要同时加载，不易操作，而且会使管涵产生轴向压力，对加载千斤顶、反力架的最大量程要求很高，受限于试验室设备，所以未采用该加载方案。此外，试验目的仅仅是为了探索波纹钢加固钢筋混凝土管的力学特性，两点加载方案能够得到基本的受力特征，这对研究来说是足够的。试验采用的千斤顶量程为1 500 kN，安装在反力架上，千斤顶下部安装分配梁、加载垫板，防止加载产生的应力集中现象，试件下部放置在刚性地面上并设有下部加载垫板。加载速率控制在15 kN/min，如果出现较为明显的试验现象均暂停加载来观察。

2 试验现象与数据分析

2.1 5个试件的荷载-位移曲线

试验所用RCP的配筋率为0.282 6%，拉、压钢筋面积分别为310.86 mm2，钢筋混凝土管的配筋率非常接近最小配筋率0.2%，说明混凝土管的配筋非常接近少筋截面。在加载过程中，荷载达到41.7 kN时，钢筋混凝土顶部出现细微裂缝，构件开裂，荷载-位移曲线发生较大转折。由于配筋率较小，试件基本上进入强化阶段，最终的承载力为90 kN。钢筋混凝土管在开裂前表现出良好的弹性性能，开裂后的裂缝处钢筋迅速屈服并进入强化阶段，其承载能力继续增加，直到最终破坏，此时钢筋被拉断，受拉区混凝土的裂缝较宽。RCP的荷载-位移曲线如图3(a)所示，管的垂直和水平位移变化幅度相似，该曲线只有两个阶段，一个是弹性阶段，另一个是弹塑性阶段，曲线中没有明显的屈服点，钢筋混凝土管的开裂荷载Fcr为41.70 kN，极限荷载Fu为90 kN。

钢材是一种较为理想的弹塑性材料，钢制波纹钢管也具有良好的弹塑性性能。从图3(a)可以看出，在大变形情况下CSP仍然表现出良好的弹性性能。当荷载在54 kN之前时，荷载-位移曲线基本上呈直线，之后波纹钢管进入弹塑性阶段；当荷载达到极限承载力80 kN时，波纹钢管完全进入塑性阶段，其荷载-位移曲线变为水平直线。由于坐标轴的长度，图3仅绘制了弹性和弹塑性阶段的一部分，未绘制曲线的塑性阶段，该弹性及弹塑性阶段足以分析波纹钢加固钢筋混凝土管的基本力学特性。

图3 RCP、CSP、RGC、ERGC和RG的荷载-位移曲线

Fig.3 Load-displacement curves of RCP，CSP，RGC，ERGC and RG

RGC是波纹钢加固的钢筋混凝土管，其荷载-位移曲线如图3(a)所示，该曲线在达到最大值时共包含了3个峰值和2个谷值。当加载至100 kN时，管顶位置的填充混凝土下部出现细微裂缝；加载至145 kN时，管侧位置的钢筋混凝土管外侧出现细微裂缝；之后加固管进入弹塑性阶段，直至达到荷载-位移曲线的第一峰值，此时荷载为230.81 kN，竖向位移为2.83 mm；随着试验的进行，同心加固管的填充混凝土进一步开裂，引起荷载短暂降低，继而荷载稍有增加，与第一峰值对应的荷载基本相等，但位移增大，类似于位移跳跃现象；继续进行加载时，发现力传感器的读数降低，位移传感器的读数增加，荷载-位移曲线出现了第二谷值(荷载为193.00 kN，竖向位移为8.03 mm)，此时是由于填充混凝土的进一步开裂、波纹钢管与填充混凝土发生部分滑移引起的，这时填充混凝土在管顶、管底产生较长的裂缝，暂时没有贯通；继续加载，同心加固管进入强化阶段，承载力有所提高，在加载过程中产生了钢材的响声，波纹钢管开始发挥较大作用，最终的极限承载力为255.94 kN，钢筋混凝土管和填充混凝土均出现了贯通裂缝。从波纹钢的荷载-位移曲线可以看出，位移很小时，波纹钢管提供的荷载很小，只有位移很大时，波纹钢管才能提供较大的荷载。根据同心加固管的荷载-位移曲线，第一个峰值Fd=230.81 kN之前的曲线较为圆滑，没有荷载跳跃现象，波纹钢管处于弹性阶段，残余变形较小(卸载后可以恢复大部分变形)。因此，本研究以第一峰值对应的荷载作为加固管的试验承载力，与其对应的竖向位移为2.83 mm。

ERGC是波纹钢管竖向偏心加固的钢筋混凝土管，其荷载-位移曲线见图3(b)。从图3(b)中可以看出，偏心加固管与同心加固管的荷载-位移曲线的形状相似，但峰值、谷值有所不同。当荷载达到105 kN时，管顶位置的填充混凝土下部出现裂缝；当荷载达到210 kN时，管侧位置的钢筋混凝土管外侧出现裂缝。其他试验现象与同心加固管相似，但由于偏心加固管中的波纹钢管与钢筋混凝土管在管底紧密接触，缺少填充混凝土，因而其第一峰值(Fd2=164.60 kN)远小于同心加固管的第一峰值(Fd1=230.81 kN)。同时，偏心加固管的第一峰值对应的竖向位移u2为1.10 mm，也小于同心加固管的竖向位移u1(2.83 mm)，表明偏心加固管的承载力低于同心加固管。

RG是仅用填充混凝土加固的钢筋混凝土管，通过波纹钢充当内模板并在填充混凝土凝结硬化后刨掉波纹钢管之后形成的试件，无波纹钢加固管的荷载-位移曲线如图3(c)所示，为方便结果对比，图中同时绘出了同心加固管的荷载-位移曲线。当荷载达到125 kN时，管顶位置的填充混凝土下部出现裂缝；当荷载达到195 kN时，管侧位置的钢筋混凝土管外侧出现裂缝；之后，试件的承载力继续增加，直至达到最大承载力280.00 kN。从图3(c)中可以看出，无波纹钢加固管的荷载-位移曲线只包含一个峰值和一个谷值，其极限承载力高于同心加固管，并且达到同心加固管的荷载-位移曲线第一个峰值之前，这两个试件的荷载-位移曲线基本重合。这间接反映出，在曲线的第一个峰值之前，试件的承载力主要取决于钢筋混凝土管和填充混凝土，波纹钢管发挥的作用很小。无波纹钢加固管的荷载-位移曲线没有第二和第三峰值，这是由于缺乏波纹钢管所致。从图3(c)中还可以看出：加固管的承载力在第一个峰值前主要取决于钢筋混凝土管和填充混凝土，第二个谷值至第三个峰值之间的承载力由钢筋混凝土管、填充混凝土和波纹钢管共同提供，波纹钢管从第二个谷值之后开始发挥作用；同心加固管的荷载-位移曲线有明显的加强阶段(第二个谷值至第三个峰值)和较好的延性(破坏后具有较大的变形能)，这说明研究采用的小波形波纹钢管的主要作用是改变构件的破坏模式，对承载力的贡献不大。由于第一个峰值应作为试验承载力的设计值，因此两个试样的承载力分别为Fd1=230.81 kN(同心加固管)，Fd3=280.00 kN(无波纹钢加固管)，与第一个峰值对应的竖向位移分别为u1=2.83 mm、u3=7.90 mm。

2.2 粘结情况的判别

加固后管涵端面的裂缝分布如图4所示。观察到波纹钢管和填充混凝土在管侧出现较为明显的分离现象，同时在混凝土管和填充混凝土中分别出现受拉区和受压区，根据叠合梁的受力机理，可以推测出混凝土管和填充混凝土并不是完全粘结的，至少存在滑移趋势。试验完成后，将试件沿裂缝位置切断，发现填充混凝土与钢筋混凝土管是相互脱离的，填充混凝土的外表面光滑、无粘结(靠近混凝土管一侧)，与波纹钢管一侧也是相互脱离的。从这个现象推测出，填充混凝土与钢筋混凝土管出现滑移现象，并未完全粘结在一起。

因为混凝土是一种粘结材料，所以填充混凝土和混凝土管之间肯定存在粘结，不是完全滑移的，但根据图4所示的裂缝分布和填充混凝土剥离现象，意味着它们并没有完全粘合。现实可能介于这两种情况之间，可能在管顶、管底粘结，管侧脱离；也可能是它们之间存在粘结力(也可能是摩擦力)，但这个力的大小不足以抵抗滑移。

图5给出了不同粘结情况下的截面应力分布情况，假设钢筋混凝土管、填充混凝土和波纹钢管是完全弹性的材料，因为图5仅用于分析它们的粘结情况，所以并未考虑它们实际的材料特性。完全组合时，截面应力分布呈直线型，加固管中只有一个受拉区和一个受压区，波纹钢管在管顶和管底是全截面受拉的，在管侧是全截面受压的；钢筋混凝土管在管顶和管底是全截面受压的，在管侧是全截面受拉的；如果混凝土中存在裂缝，这个裂缝一般会贯通填充混凝土，显然实验现象与此不符，所以加固管不是完全粘结的组合体系。完全滑移时，3个管体的应力分布应呈现折线形状，每个管体中均存在受拉区和受压区，裂缝将分别存在于钢筋混凝土管和填充混凝土中，裂缝不会贯通，实验现象与此相符，但由于混凝土的粘结性和表面粗糙度，混凝土管、填充混凝土和波纹钢管也不可能是完全滑移的。

如果不是上述两种情况，加固管很可能是介于两者之间的一种情形，如图5所示的“介于两者之间”的情况，并将粘结作用(或摩擦作用)以粘结力表示出来，由于粘结力的方向与相互滑动方向相反，所以总是降低3个管体的弯曲应力；由于波纹钢管内侧和混凝土管外侧没有其他材料接触，所以这两个面上的粘结力为0；粘结力对填充混凝土的影响最大，分别降低了它的拉、压应力水平，提高了填充混凝土的抗裂性能；这种粘结力可以在填充混凝土开裂的情况下阻碍裂缝的进一步发展，类似裂缝处存在抗力，这在一定程度上使得填充混凝土能够承受一些弯矩。此外，管侧处存在轴向压力，这个压力对管侧承受弯矩是有利的，暂且不考虑混凝土管和波纹钢管(因为他们自身可以承受弯矩)，这个压力能够使填充混凝土的抗弯承载力更高。粘结力和轴向压力的作用使填充混凝土即使开裂，也能够抵抗弯矩作用，而不是一旦开裂就立即退出工作。

同心加固管的承载力达到第一峰值(230.81 kN)时波纹钢的截面应力与弯矩见图6。应力根据应变乘以钢材弹性模量换算得到；弯矩根据波峰、波谷的弯曲应力乘以抗弯惯性矩、除以截面高度的一半得到，弯曲应力为实测应力扣除轴压应力。从应力分布来看，波纹钢管在管顶、管底位置外侧受压、内侧受拉；在管侧位置外侧受拉、内侧受压，这也说明了波纹钢管与填充混凝土未完全粘结。根据波纹钢管管顶、管底的弯矩值反算波纹钢管分担的集中力大小F1=2×(1.77+0.67)/0.512=9.53 kN，这与波纹钢管的荷载-位移曲线中的6.57 kN(波纹钢管与同心加固管达到相同变形(u1=2.83 mm)时波纹钢管单独承担的荷载)比较接近，这说明波纹钢管在加固体系中是单独工作的，并未与混凝土形成组合结构。

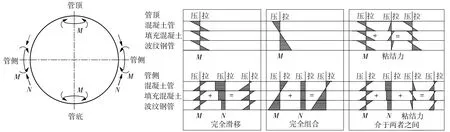
图5 不同粘结情况下的截面应力分布Fig.5 Stress distribution of cross section under different bonding conditions

图6 波纹钢管的截面应力与弯矩Fig.6 Stress and bending moment of CSP

3 承载力估算

3.1 同心加固管的承载力估算

理论分析通常是对实际结构做一些简化，在较为理想的情况下进行理论推导，从而获得承载力的计算方法。由于部分粘结的加固管难以从理论上进行承载力推导，因此暂且忽略钢筋混凝土管、填充混凝土和波纹钢管接触面上的粘结力或摩擦力，假定它们之间是完全光滑的；粘结力或摩擦力能够为填充混凝土提供抗拉强度，使其能够单独承受弯矩；这种假设推导出的承载力为实际承载力的下限值，而采用完全组合理论计算的承载力为实际承载力的上限值，工程设计中采用下限值能够使设计更为保守。

由图3(a)可知，当钢筋混凝土管、波纹钢管的位移等于同心加固管荷载-位移曲线的第一个峰值所对应的位移时，波纹钢管处于弹性阶段，而钢筋混凝土管处于弹塑性阶段。填充混凝土单独工作时，填充混凝土不能够独自承受弯矩，一旦开裂就退出工作。如图7所示，在加固体系中，填充混凝土位于钢筋混凝土管和波纹钢管之间，受到两个管的径向约束力，这个约束力使填充混凝土受弯时不会在垂直方向上产生较大的位移；并且开裂位置受到环向粘结力(或摩擦力)的抵抗，使填充混凝土即使开裂也能在裂缝一侧产生抗力(粘结力提供的假想抗拉应力)；这两种因素共同作用使填充混凝土在加固管中可以承受弯矩。如果将环向粘结力看成是填充混凝土的抗拉应力，那么可以假想成加固管中的填充混凝土可以受拉、也可以受压，所以才能够假设填充混凝土是弹性的。因此，采用弹性刚度来分析填充混凝土和波纹钢管，采用短期刚度Bs分析混凝土管(短期刚度值适用于短期荷载条件)。混凝土构件的刚度可采用《混凝土结构设计规范》[13]计算，其表达式如下：

(1)

(2)

式中，Bs是混凝土的短期刚度，Es是钢筋的弹性模量，As是受拉钢筋的截面面积，h0是混凝土管的有效壁厚，ψ是应变不均匀系数，αE是弹性模量比值，ρ是受拉钢筋配筋率，γ′f是T形截面受压翼缘面积与腹板有效截面面积的比值(矩形截面应取0)，ftk是混凝土抗拉强度标准值，ρte是受拉钢筋的有效配筋率，σsq是裂缝处钢筋的拉应力。

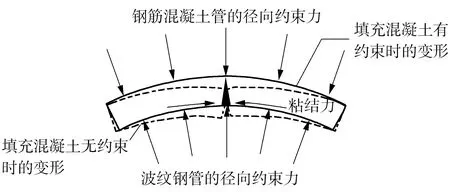
图7 填充混凝土的受力模式Fig.7 Stress mode of the grout

文中分别采用下标1、2和3代表波纹钢管、填充混凝土和混凝土管，则在图8的受力模式下，其竖向位移可表示为[14]

(3)

(4)

(5)

式中，F1、F2和F3分别是波纹钢管、填充混凝土、混凝土管与加固管的设计承载力对应的变形相同时能够提供的承载力，r1、r2和r3分别是波纹钢管、填充混凝土和混凝土管的平均半径，E1和E2分别是波纹钢管和填充混凝土的弹性模量，I1和I2分别是波纹钢管和填充混凝土的抗弯惯性矩。

因为假定波纹钢管、填充混凝土和钢筋混凝土管接触面光滑，所以在两点加载的情况下，3个管体的竖向位移应相等(Δ1=Δ2=Δ3)，可得

图8 集中荷载作用下管的变形Fig.8 Deflection of the pipe subjected to the concentrated load

(6)

各个管体分担的集中荷载应该满足

F1+F2+F3=F

(7)

式中，F是加固管承担的集中荷载。

将式(6)代入式(7)，可得

(8)

如果已知混凝土管的承载力，那么通过式(8)可计算加固管的承载力。当加固管的承载力到达第一个峰值时，其竖向变形为2.83 mm，混凝土管的变形达到2.83 mm时能够提供的承载力F3=52.90 kN(如图3所示)，Es=2.1×105MPa，Ec=3.35×104MPa，As=310.86 mm2，h0=110 mm，ψ=0.313，αE=6.27，ρ=0.002 826，ftk=2.51 MPa(C45混凝土的抗拉强度标准值)，ρte=0.005 181，σsq=400 MPa(钢筋屈服强度)，混凝土管的r3=660.0 mm，根据式(1)计算得到Bs=1 185 558 754 087 MPa·mm4。因为填充混凝土的截面不规则，它的抗弯惯性矩可以借助绘图软件(如AutoCAD)获得，E2=3.00×104MPa，E2I2=1 783 217 430 000 MPa·mm4。波纹钢管的抗弯惯性矩可以直接查制造商提供的参数表，或者借助绘图软件计算，I1=364 107 mm4，E1I1=55 462 470 000 MPa·mm4。波纹钢管和填充混凝土的平均半径分别为r1=512.5 mm，r2=550.0 mm。当上述参数全部求解之后，加固管的承载力可通过式(8)计算得到F=195.7 kN，这个值比试验得到的承载力(230.81 kN)低。而无波纹钢加固管最大承载力对应的位移是7.90 mm，同样变形时，混凝土管的承载力为76.90 kN，以此荷载作为F3，计算得到无波纹钢加固管的承载力为276.80 kN，这个值与试验得到的承载力(280.00 kN)接近。

3.2 偏心加固管的承载力估算

如果管涵的截面是同等厚度的，塑性铰一般形成在弯矩较大的截面，力学分析时通常把这些容易形成塑性铰的位置简化成固定连接，从而对结构进行简化计算。如表1所示，在两点加载的情况下，同心加固管的管顶、管底和管侧处形成塑性铰(对应图9(a)中的管顶、管底和管侧裂缝，计算模型可以简化成无铰半圆拱。但垂直偏心加固管的破坏机理不同于同心加固管，如图9(b)所示两个塑性铰在管顶、管底，另外两个塑性铰在管侧偏下的位置形成(约斜下45°，塑性铰位置分别对应图9(b)中的管顶、管底和斜下部45°裂缝)，这主要是因为加固管厚度不均匀导致的，刚度小的位置更容易形成塑性铰。为了简化分析偏心加固管，假设两个塑性铰在斜向45°的位置形成，两个塑性铰包含的圆心角刚好是90°。因为管的抗弯承载力主要取决于管壁较薄的区段，因此取这两个塑性铰之间的拱进行分析，同样将其简化为无铰拱(表1所示偏心加固管的计算模型)。

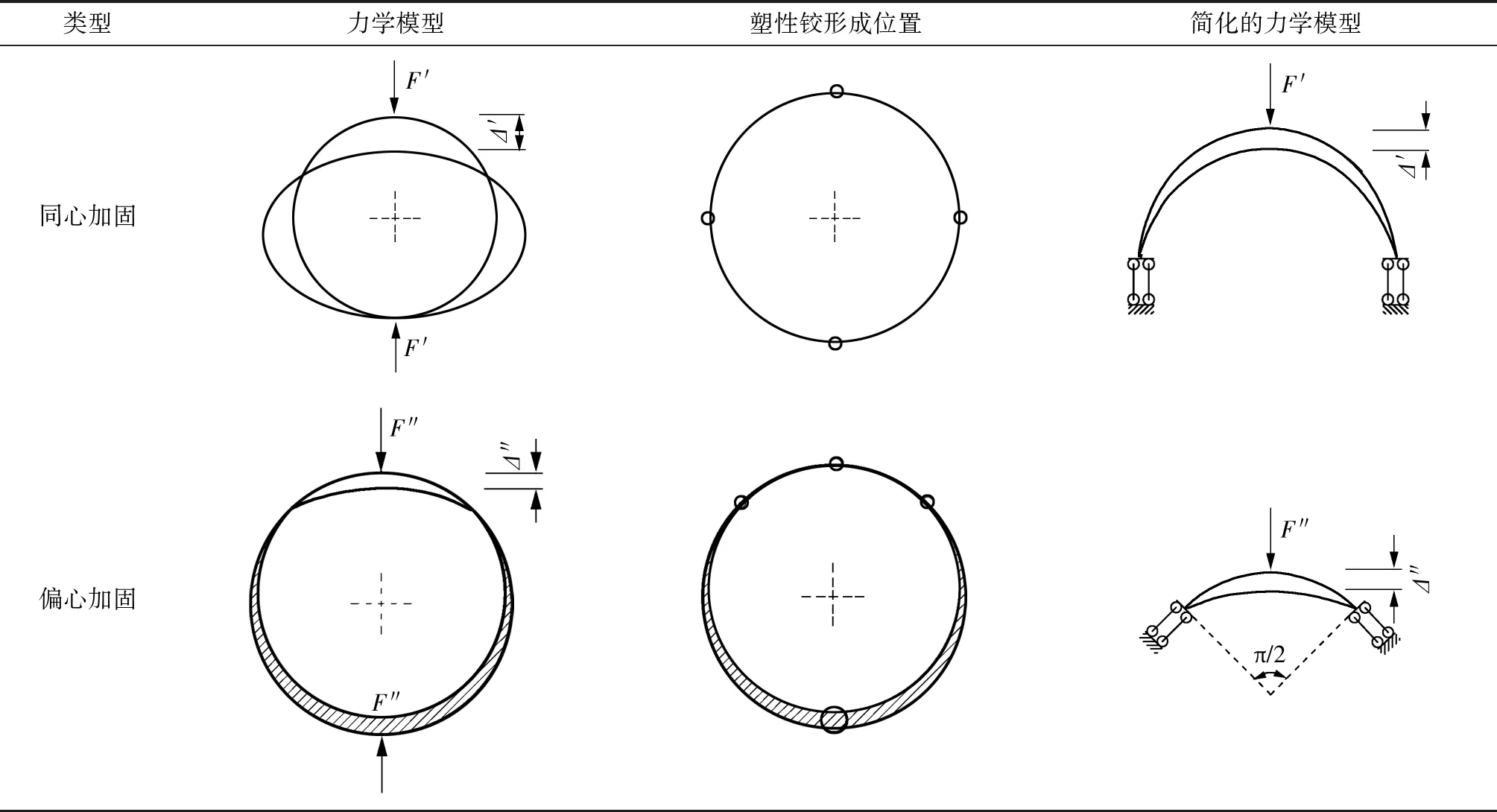
表1 同心和偏心加固管的模型Table 1 Models of the eccentric and the concentric rehabilitated pipes

图9 同心和偏心加固管的破坏机理

Fig.9 Failure mechanism of eccentric and concentric reinforced pipes

如果表1简化的力学模型中所示的两个拱(表1简化的力学模型中同心加固管实际上与图8相同，是图8结构的一半)由相同的材料、截面(EI相同)和半径R构成，则可以通过Δ′=Δ″得到F′和F″之间的关系。Δ′=Δ″分别表示为[15]

(9)

Δ″≈0.18F″R3/(EI)

(10)

则可以得到F′和F″之间的关系：

F″=2.432F′

(11)

这一关系表明，如果一个管能承受F′的力，则固定约束的四分之一圆管能承受F′力的2.432倍。换言之，如果47.80 kN的荷载引起相同截面的混凝土管产生1.10 mm的竖向位移，则必须是该力的2.432倍(2.432×47.80=116.25 kN)才能在偏心加固管中使混凝土管产生相同的竖向位移。因此，在偏心加固管中应该用2.432F3替代原公式中的F3，因为偏心加固管最薄部分只有混凝土管和波纹钢管，没有填充混凝土，E2I2应为0，式(8)可简化为

(12)

其中，F3=47.80 kN，I1=364 107 mm4，E1=2.1×105MPa，Bs=1 185 558 754 087 MPa·mm4，r1=512.5 mm，r3=660.0 mm，则偏心加固管的承载力根据式(12)计算得到的结果为127.90 kN(为试验结果的0.78倍)。

4 讨论

本研究采用两种方法来估算加固管的承载力，两种方法均假设钢筋混凝土管、填充混凝土和波纹钢管之间没有粘结，将实际存在的接触面粘结力假设为填充混凝土的拉、压应力，并未考虑粘结力的大小，钢筋混凝土管、填充混凝土和波纹钢管分别采用了短期刚度、弹性刚度。上述承载力计算方法采用的参数及计算结果见表2，其中Fc为计算的承载力，Fd为荷载-位移曲线第一个峰值对应的承载力，计算结果与试验结果的最大误差为22.3%。

计算结果表明，基于混凝土管、填充混凝土和波纹钢管不相互粘结的假设，推导出的承载力计算方法，通常能够获得实际承载力的下限值。另外，实验中无波纹钢加固管的承载力比同心加固管高，如果文中的计算方法是正确的，则可以通过理论分析解释这一现象，即无波纹钢加固管缺少波纹钢的内部支撑，当它达到最大承载力时的竖向位移较大，此时所用的混凝土管的承载力F3要高于其他试件中采用的F3，因而加固管能够提供更高的承载力。然而，从工程经验的角度来考虑，有波纹钢加固管的承载力要比无波纹钢加固管高，试验结果与此不符，很可能是由于数据采集偏差，也有可能是因为无波纹钢加固管达到极限承载力时的位移较大，所用的混凝土管的承载力较高，至于是何种原因引起，还需要进一步研究。

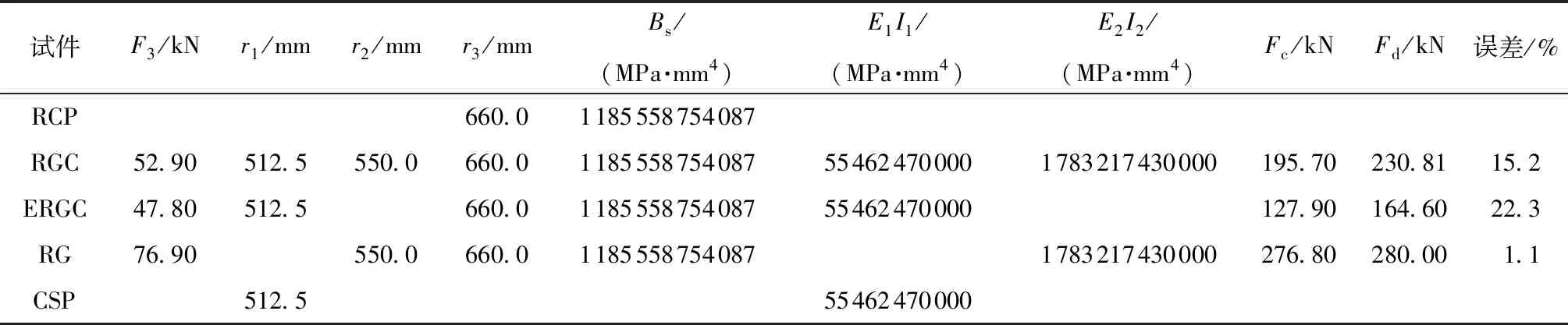
表2 试验管的计算参数及承载力计算结果Table 2 Calculation parameters of the tested pipes and the calculation results of load-carrying capacity

本研究推导出来的理论本质上是指钢筋混凝土、填充混凝土或者波纹钢对加固管承载力的贡献大小主要依赖于3种管体的“环刚度”(EI/r3或Bs/r3)，所以波纹钢管是否发挥作用、作用大小主要取决于波纹钢管的环刚度大小。试验所用的波纹钢管是小波纹、壁厚较薄，因而对加固管的承载力贡献较小，如果采用深波纹、壁厚较厚的波纹钢管，那么波纹钢管的贡献将会很大，需要进行更多的试验来研究波纹钢加固钢筋混凝土管的效果。

加固管的承载能力取的是荷载-位移曲线的第一个峰值，而不是最终的极限承载力，主要是由于该曲线出现了荷载跳跃现象，如果取极限承载力，这对工程来讲是非常不可靠的。另外，荷载跳跃之后，钢筋混凝土管、填充混凝土和波纹钢管不再符合研究假设，波纹钢管中的应力发生突变，将会很快进入塑性阶段，那么极限承载力需要采用塑性理论进行分析。

5 结论与展望

文中采用5个试件进行试验，研究了波纹钢管加固钢筋混凝土管的力学性能，得到其荷载-位移曲线，并基于钢筋混凝土管、填充混凝土和波纹钢管相互不粘结的假设推导出承载力估算方法，得到以下主要结论：

(1)波纹钢加固钢筋混凝土管确实提高了原有管涵的承载能力和刚度，加固后的钢筋混凝土管的承载能力主要取决于钢筋混凝土管和填充混凝土，波纹钢管在此次试验中发挥的作用很小；

(2)由于钢筋混凝土管和波纹钢管在管底紧密接触、无填充混凝土，偏心加固管的试验承载力低于同心加固管，并且偏心加固管的破坏模型与同心加固管不同；

(3)计算结果表明，基于无粘结假设推导出的同心、垂直偏心加固管承载力计算公式，能够计算加固管的承载力，计算结果与试验结果的误差小于22.3%，而且计算值是试验值的下限，这对工程设计是有利的。

虽然本文探讨了小波形波纹钢加固钢筋混凝土管的效果，提出了一种估算加固管承载力的方法，但试验采用的波纹钢是小波形，对承载力的贡献较小，而且出现了无波纹钢加固管的承载力高于有波纹钢加固管的承载力，这与常识不符，需要进一步验证和探讨这种现象是否存在于其他波形的波纹钢加固管中，还是仅存在于小波形的波纹钢加固管中，亦或是数据采集误差。此外，本研究提出的承载力估算方法仅基于5个试件的试验结果，其试件数量过少，不足以给出通用性结论，需要在今后研究中增加试件个数，以获得更为一般性的结论。此外，还需要进一步研究接触面粘结力的分布及其对加固管承载力的影响。