基于随机森林算法的制冷剂充注量故障诊断

周璇 王晓佩 梁列全 闫军威

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640;2.广东财经大学 信息学院，广东 广州 510320)

制冷主机是制冷系统的重要组成部分，随着制冷技术与生产需要的发展，制冷主机运行过程呈现大型化、复杂性、非线性、大功率等特性。制冷主机故障直接影响制冷系统运行的经济性、高效性和合理性[1]。制冷主机故障检测与诊断(FDD)是指监测制冷主机各种运行状态，通过各种技术判断其是否发生故障，分析故障发生的原因，及时对可能发生的故障或已发生的故障进行预报或报警，对于保证制冷系统安全运行，减少制冷系统设备磨损以及系统节能降耗具有重要的意义[2]。

制冷主机主要由制冷剂循环、水循环、油循环3类回路系统组成。制冷剂循环回路包括低压和高压回路两部分，低压部分指制冷剂离开节流阀进入蒸发器，经过吸气管到达压缩机吸气阀的那部分循环回路，这部分管道和设备中制冷剂的压力接近蒸发压力，故称为低压系统；另一部分是指制冷剂从压缩机排气阀经排气管、油分离器、冷凝器、泄液管、贮液器、高压输液管到达节流阀的那部分循环回路，这部分管道和设备中的制冷剂压力接近冷凝压力，因此称其为高压系统。对于未设置高压储液器和低压汽液分离器的制冷系统，制冷剂的充注量控制尤其重要。制冷剂充注量过高会储存在冷凝器中，淹没冷凝器散热簇管，使散热面积减小，冷凝压力升高，导致制冷量下降。制冷剂充注量不足会导致蒸发器换热面积不足，降低换热效率，无法满足末端用能需求。制冷剂泄漏是导致制冷剂充注量不足的原因之一，基于现有制冷剂低环保、易燃、易爆等特性，制冷剂泄漏可能会导致环境污染、火灾甚至爆炸。制冷剂充注过量导致其在蒸发器中无法完全换热，过热度低，制冷压缩机液击。此外，制冷剂充注量异常还会使系统膨胀阀调节波动大，严重降低系统稳定性、安全性、高效性。Comstock等[3]通过对离心式制冷系统重要故障进行统计分析，发现制冷剂充注量异常是一种典型的故障，其发生频率较高，且后果较为严重。目前，制冷剂充注量的准确检测与控制仍是制冷系统控制的一大难点，科学有效的监测制冷剂充注量对制冷系统运行状态的识别具有重要的意义。张良俊等[4]通过实验研究了充注量对制冷系统部分性能参数及稳定性的影响，为系统的最佳充注量提供了依据。孔祥强等[5]建立了热泵系统数学模型，并用数值模拟对系统充注量和部分运行参数的关系进行研究，寻求最佳充注量。但以上研究主要是对制冷系统单一运行参数分别进行研究，参数的选择根据经验人为判定，且单一数据特征有时并不能充分反映机组运行状态的时变性与多样性[6]。与此同时，大数据给空调机组运行状态监测及故障诊断的深入研究和应用提供了新的机遇[7]。梁晴晴等[8]针对制冷系统常见的7种故障，提出了基于主元分析-概率神经网络的制冷系统故障诊断方法，提高了诊断正确率，缩短了诊断时间。卿红等[9]结合最小二乘支持向量机和粒子群算法提高了制冷剂泄漏的故障诊断准确率。王江宇等[10]针对多联机系统制冷剂充注量故障，结合主成分分析与决策树优点，提出了基于主成分分析-决策树(PCA-DT)的制冷剂充注量故障检测与诊断方法。袁玥等[11]针对多联机制冷剂充注量的故障，提出了基于主成分分析和神经网络相结合(PCA-BP)的诊断方法，相比传统的BP神经网络算法，缩减了故障的诊断时间，节省了系统的存储空间，提高了诊断精度。Cotrufo等[12]针对不同工况建立基于主成分分析的模型，设置椭圆离群范围，进而确定异常模式，实现对空调系统的故障诊断。Li等[13]结合PCA与支持向量机(SVM)方法对冷水机组故障检测与诊断方法展开了研究。Hu等[14]利用PCA对制冷系统传感器故障进行了敏感性分析。Guo等[15]针对多联机故障，提出了基于模块化PCA模型和基于专家规则的故障诊断方法，并通过实验验证了该方法诊断多联机故障的有效性。Li等[16]通过对原有的PCA算法进行改进，提出了基于密度聚类和主元分析的螺杆冷水机组故障诊断方法，结果表明该方法的平均绝对百分误差(MAPE)值较原方法低，诊断效果更好。上述研究在采集大量数据的基础上，大多采用PCA与其他算法相结合的方法进行数据降维和故障诊断，通常在保留数据特征的同时，能很好地去除了信息的冗余，降低了数据维度。然而，数据通过PCA方法处理后，其数学特征得以很好保留的同时，却丢失了其物理意义。

上述研究主要对制冷剂充注量不足、制冷剂充注量正常、制冷剂充注过量3种状态展开研究，缺少对制冷剂充注量故障严重程度进一步的细化分析。为此，文中针对离心式冷水机组的制冷剂系统，提出了一种基于随机森林算法的制冷剂充注量故障监测与诊断方法。

1 故障诊断框架

制冷系统制冷剂充注量故障诊断通过对制冷剂的充注量进行在线监测，准确确定制冷剂充注量，评估故障严重程度，进而采取有效的措施减少故障可能带来的危害。基于随机森林算法的制冷剂充注量故障监测与诊断流程包括数据预处理、特征选择、故障诊断3部分，如图1所示。

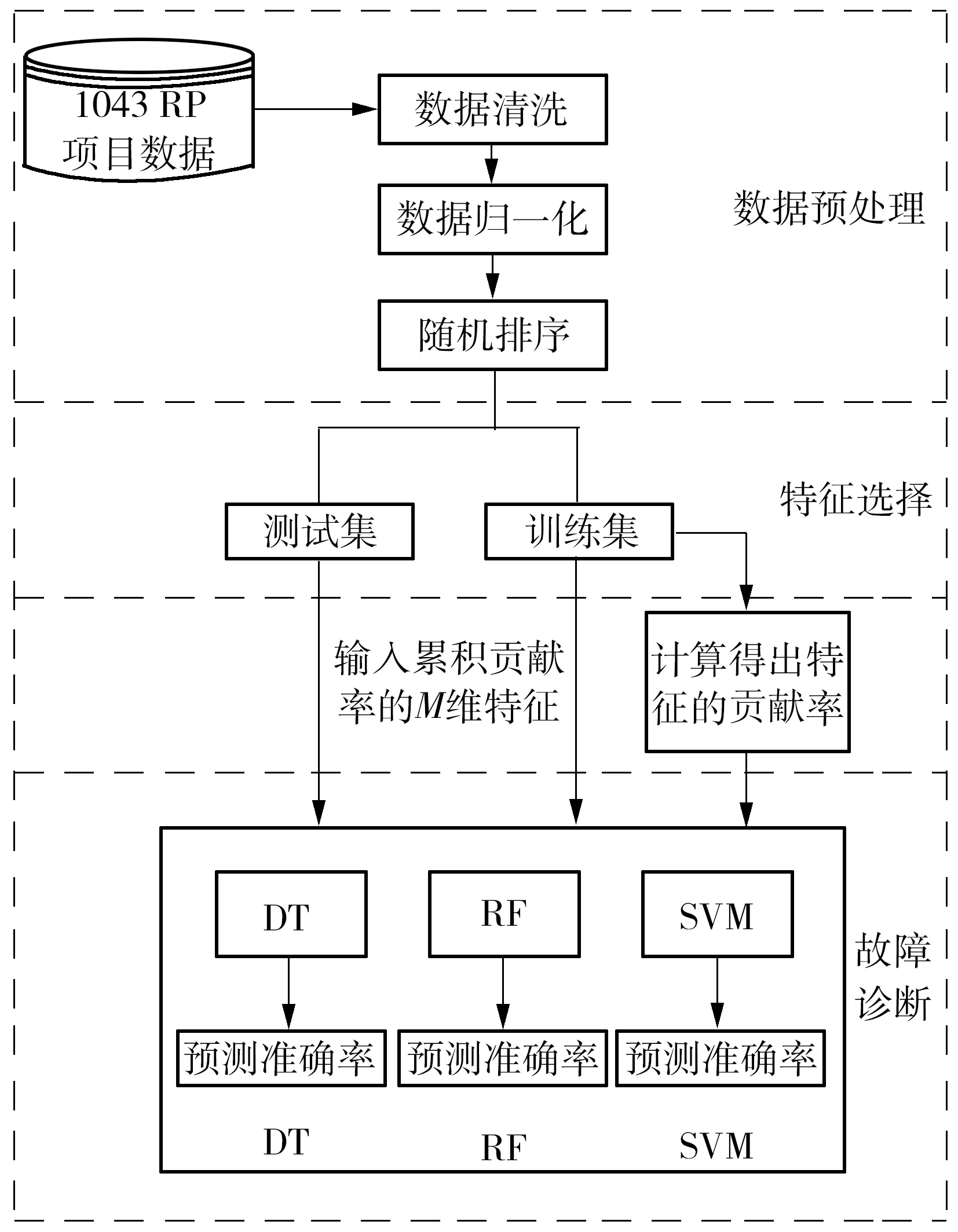
图1 故障诊断框架Fig.1 Framework of fault diagnosis

首先对数据进行预处理，将数据划分为训练集和测试集；然后采用随机森林基尼指数特征选择方法量化训练集中故障特征量的重要性，并选取训练集中重要的故障特征量作为RF算法的输入，建立故障诊断模型；最后输入测试集相应的故障特征量，对制冷剂的充注状态进行识别和分类，以此算出分类的准确率，得到低维度输入下的高精度故障诊断输出。具体的步骤如下：

(1)数据预处理 数据预处理包括数据清洗、数据归一化。数据清洗主要是剔除异常值、死值等；数据归一化用于尽可能降低量纲和数量级差异所带来的影响。

(2)特征选择 采用基于随机森林基尼指数平均不纯度减少的特征选择方法对训练集特征进行贡献率排序，量化特征的重要性，进而选取贡献累计率较高的值作为诊断模型的输入，以降低诊断成本。

(3)故障诊断 选取训练集M维故障特征量，以诊断准确率P作为随机森林算法优化的目标函数值

(1)

式中，ncorrect为测试集正确诊断样本量，Ntotal为测试集样本总量。

通过对训练集进行建模，得出不同维度故障特征量条件下，不同样本规模下RF算法的诊断准确率。

2 随机森林算法

随机森林算法是将Bagging集成学习理论与随机子空间方法相结合的一种有监督机器学习算法[17]。随机森林算法是以决策树为基分类器，在决策树的基础上，通过引入集成思想增加算法的随机性，大大提升了算法的适用范围。集成思想增加了决策树的差异性，训练集抽取的随机性和节点候选分割特征集合的随机性增加了决策树的多样性，而差异性和多样性使算法的泛化能力和诊断精度得到提升[18]。随机森林算法主要包括决策树生成和分类诊断，如图2所示。决策树生成过程主要包括样本随机选择、特征随机选取、最优分割点筛选和树的生长4部分。随机森林算法的具体步骤如下：

(1)样本选择 从样本集合中进行独立重复抽样，选取n个样本得到一个样本集，重复K次得到K个样本集。

(2)特征选择 每个样本集为一棵独立决策树，假设含有M个输入特征，则在树的节点处随机挑取m个特征作为候选特征集。

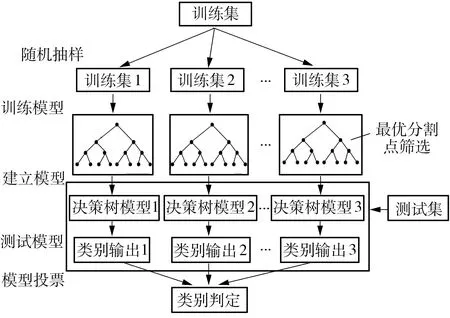
图2 随机森林算法的结构Fig.2 Structure of random forest algorithm

(3)最优分割点筛选 按照一定的原则从候选特征集中选取最优特征作为节点进行分裂。随机森林构建决策树常用的方法主要有ID3、C4.5、CART算法，其中ID3、C4.5算法基于信息熵原理选择分裂特征，CART算法以基尼指数为分割原则，泛化能力比前两种算法好[19]，因此文中以基尼指数为分割原则，优先选取贡献率高的特征为最优特征。

在分类问题中，假设有K个类、第i棵决策树、样本集合D，则基尼指数为

(2)

式中，Ck是D中属于第k类的样本子集。

如果样本集合D根据特征A是否取某一可能值a被分割成D1和D2两部分，则在特征A条件下，集合的基尼指数定义为

(3)

则特征A在第i棵决策树这个分裂节点的重要性为

Vi(A)=G(D)-G(D,A)

(4)

(4)递归步骤(2)、(3)进行分支，直到满足要求。每棵树最大限度地生长，不进行剪枝操作。

(5)重复上述步骤k次，生成多棵分类树，同时将生成的多棵分类树组成随机森林，用随机森林分类器对新的数据进行判别与分类，分类结果按树分类器的投票多少确定。

数据特征选择旨在选取累积贡献率较高的值作为诊断模型的输入，文中基于随机森林基尼指数进行特征贡献率排序，以减少数据间的冗余性。基于随机森林基尼指数的特征贡献率排序原理如下：

首先求出特征A在n棵树的总体重要性

(5)

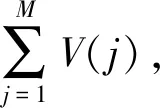
(6)

3 案例分析

3.1 实验数据

建模数据来自ASHRAE 1999年提供的制冷主机故障数据库，该实验装置的状况可以代表典型的建筑制冷机组状况[3]。实验对象是一台90冷吨(约316 kW)的离心式冷水机组(如图3所示)，其中制冷剂为R134a，蒸发器和冷凝器为壳管式换热器。该系统的主要环路系统包括制冷剂系统和水路系统，制冷剂系统包括主制冷剂环路和两条辅助制冷剂环路(用于冷却动力设备压缩机及电机和膨胀阀旁通流量调节)；水路系统包括冷冻水环路、冷却水环路、热水环路、城市供水和蒸汽供应环路。

实验主要通过按照比例过量充注制冷剂或释放制冷剂，模拟制冷剂充注量异常的不同故障。针对不同充注量的制冷剂故障分别进行实验，每次实验中通过调节冷冻水出水温度、冷却水进水温度、主机负荷3个变量模拟制冷系统典型的工况，每个变量有3个设置范围，形成3×3×3=27种典型工况。实验数据中共采集65维故障特征量，其中传感器直接测量获得的参数49维，间接计算获得的参数16维，为了更好的应用于工程实际，仅对传感器直接测量获取的参数进行处理。本文主要针对制冷剂充注量偏离正常阈值的典型全局故障展开研究。制冷剂充注量共有9种状态，如表1所示。采样周期为10 s，每种状态采样时长为51 910 s，共计5 191组数据，9种状态下共有46 719组数据。

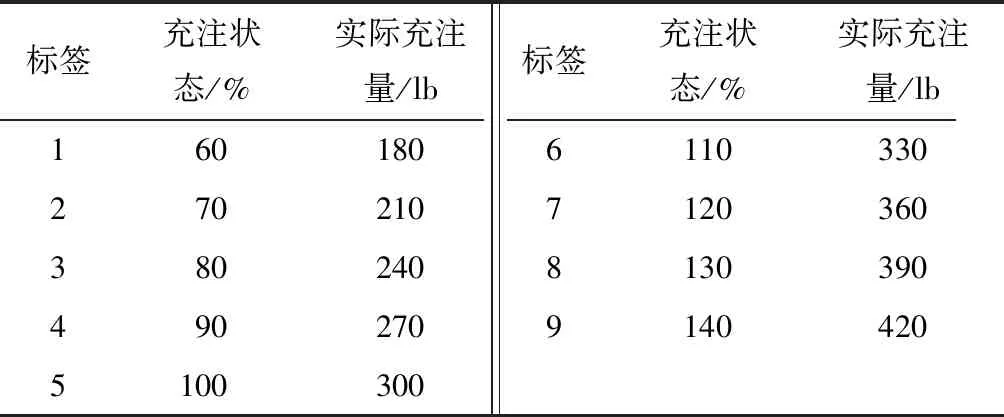
表1 制冷剂充注量的程度Table 1 Degree of refrigerant charge

3.2 实验数据预处理

通过对数据库内数据的观察，发现存在以下几种情况：

(1)部分实验数据在整个实验过程未发生变化，此类死值数据不影响故障诊断效果，直接剔除该维数据。

(2)部分实验数据在某一时刻产生突降现象，与前后数据差距极大，突变后会迅速回归正常，主要是实验过程中数据间传输产生的噪声干扰，产生时间极短，分析其原因为非工况因素引起，采用拉依达准则直接予以剔除。

(3)系统在刚开机或关机后一段时间内的所有数据均处于极其不稳定状态，这些数据不适用于故障诊断建模，因此剔除开、关机阶段的数据。

(4)由于数据量纲不同，数据的数据级相差较远，不利于数据的分析。因此，对实验数据进行归一化预处理，以消除量纲差异造成的影响。

文中提及的数据预处理主要包括数据清洗、数据归一化两部分。数据清洗主要用于剔除死值、突变值等干扰故障检测结果的异常数据以及开关机时的不稳定数据；数据归一化指对不同量纲的数据进行归一化处理。

3.2.1 数据清洗

结合数据特点，对数据的清洗过程包括剔除死值、开关机阶段不稳定数据及突变值。实验研究的49维故障特征量中部分变量为常数，一直未发生变化，如水路系统中热水阀开度和蒸汽阀开度、单元状态与激活故障四维数据，因此剔除这4组参数。任选一组实验工况如图4所示，图中包括冷冻水出水温度(TEO)、冷却水进水温度(TCI)、总负荷(ET)(间接表征主机负荷)，其中开机阶段(0～1 000 s)及关机阶段(50 500～51 900 s)的数据发生突变，因此剔除开、关机阶段产生的数据，选取的时间范围为制冷主机启动后1 000～50 500 s。由于数据采集过程中存在异常突变数据，采用拉依达准则(如式(7)、(8)所示)对不合理数据进行剔除，得到44 928组数据。

(7)

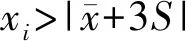
(8)

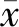
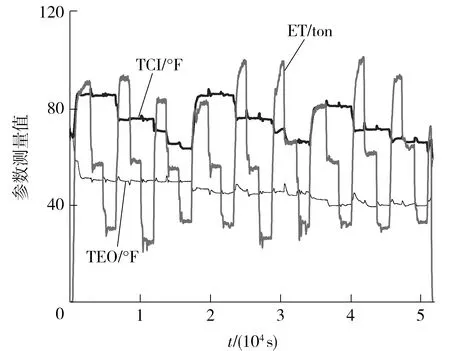
图4 工况图Fig.4 Working chart

3.2.2 数据归一化

由于模型输入的不同故障特征量具有不同的量纲和数量级，从而存在着不可公度性。为了尽可能降低量纲和数量级差异带来的影响，需要对不同类型的输入数据进行量纲归一化处理。选取9组不同充注状态的数据集，数据总量为44 884条，45维故障特征量。针对该数据集9组不同充注量进行标记，如表1所示。训练集和测试集按照3∶1进行随机抽取。首先针对训练集进行数据归一化，将数据约简到[-1，1]之间，如式(9)所示；然后对测试集采用相同的规则进行归一化，以确保归一化后数据的一致性。

(9)

式中，ymax=1，ymin=-1，xmax、xmin分别为该训练集的最大值和最小值。

3.3 基于随机森林算法的故障特征量排序

本文针对训练集筛选后的45维故障特征量，基于随机森林的基尼指数准则确定参数的重要程度，进行特征贡献率排序，评估故障特征量对故障诊断的重要度，进而指导实际工程中空调故障诊断采集参数的数量及频率，有效减少采集和存储成本，提高诊断效率。首先选取训练集5 000组数据，建立RF模型，其中RF模型参数参考Python 的scikit-learn v0.20 版本默认值设置，然后基于RF的基尼指数准则量化不同特征的贡献率。表2为重要故障特征量累积贡献率排序结果，图5为各特征量贡献率随故障特征量的变化情况。

表2 重要特征量的故障贡献率排序结果

Table 2 Fault contribution ranking of important characteristic quantities

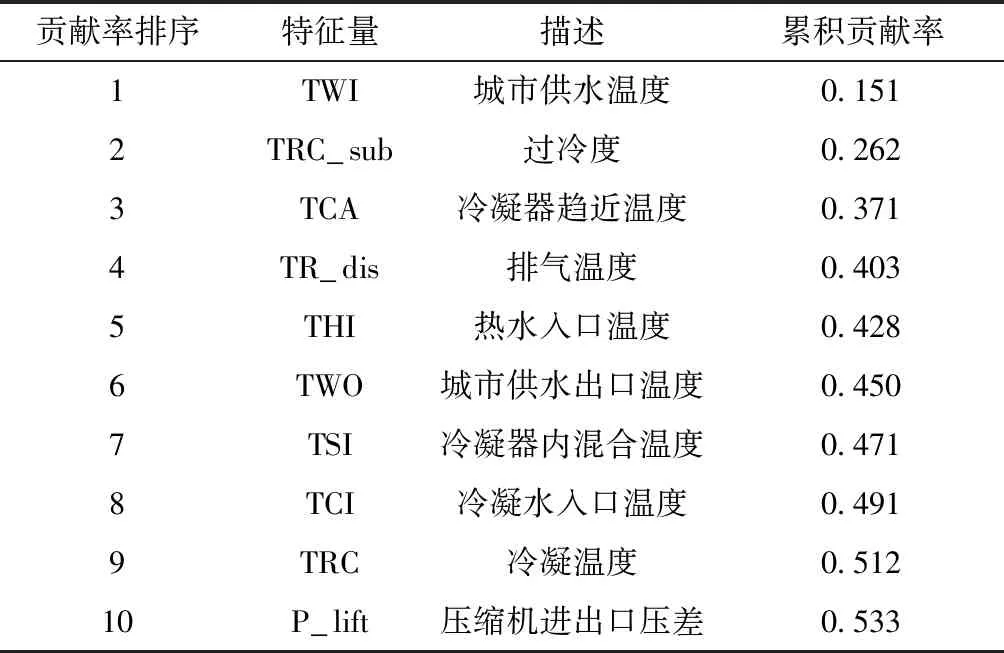
贡献率排序特征量描述累积贡献率1TWI城市供水温度0.1512TRC_sub过冷度0.2623TCA冷凝器趋近温度0.3714TR_dis排气温度0.4035THI热水入口温度0.4286TWO城市供水出口温度0.4507TSI冷凝器内混合温度0.4718TCI冷凝水入口温度0.4919TRC冷凝温度0.51210P_lift压缩机进出口压差0.533

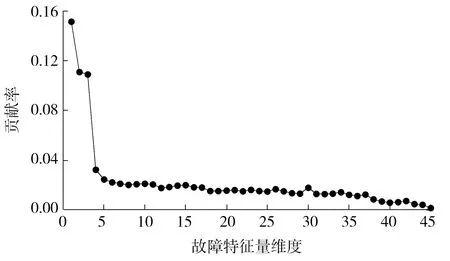
图5 贡献率随故障特征量的变化趋势Fig.5 Change of contribution rate with fault characteristic

由表2可知，对制冷剂充注量异常诊断的贡献率最高的前3个故障特征量为TWI、TRC_sub和TCA。

1)TWI(城市供水温度)

TWI为系统的外部参数，由回路示意图可知，低温的城市供水在换热器中与冷却水进行换热，吸收室内的热量，然后与外界大气发生换热而使本身温度降低，再次进入冷凝器中。城市供水温度一方面与冷却水回路进行热量交换，直接影响冷水机组的冷凝温度与制冷性能；另一方面，城市供水温度受到外界环境参数的影响，间接反映了制冷系统冷负荷的大小,且冷负荷大小直接影响制冷主机的运行状态与制冷剂循环性能。因此，当制冷剂充注量异常时，制冷剂循环状态发生改变，TWI参数能够表征此类故障特征，且贡献率最高。

2)TRC_sub(过冷度)

过冷度是冷凝器出口的冷媒压力对应的饱和温度与冷媒实际温度之间的差值。TRC_sub表征制冷剂充注量故障特征，需要分4种情况进行讨论：

(1)当制冷剂充注过量，且在膨胀阀可有效调节范围之内时，多余的制冷剂会存储在高压储液器内。

(2)当制冷剂充注过量，且膨胀阀无法有效调节时，制冷剂以液体形式进入压缩机，多余的制冷剂会存储在冷凝器中导致冷凝压力显著升高，饱和温度升高；同时单位体积的制冷剂在蒸发器内无法充分换热,导致压缩机入口温度降低，制冷剂实际温度随压缩机入口的冷媒温度降低而降低，冷凝器出口的饱和温度与冷媒实际温度之间的差值增加。

(3)当冷凝剂充注量不足，膨胀阀能够有效调节时，高压储液器内的制冷剂能够进入制冷循环系统，补充注量不足的部分。

(4)当冷凝剂充注量严重不足，膨胀阀无法有效调节时，冷凝压力降低，单位体积的制冷剂在蒸发器内过度换热导致压缩机入口温度升高，制冷剂实际温度随压缩机入口的冷媒温度降低而降低，冷凝器出口的饱和温度与冷媒实际温度之间的差值减小。

图6为27种工况下不同制冷剂充注量的TRC_sub分布图，其中rl10、rl20、rl30、rl40分别表示制冷剂泄露10%、20%、30%、40%，ro10、ro20、ro30、ro40表示制冷剂充注量较正常范围超过10%、20%、30%、40%，正常表示制冷剂充注量在正常范围。由图中可以看出，同一工况下过冷度随着制冷剂充注量的减少而降低，但相邻工况下过冷度的分布有重合，需要结合其他参数对充注量进行诊断。

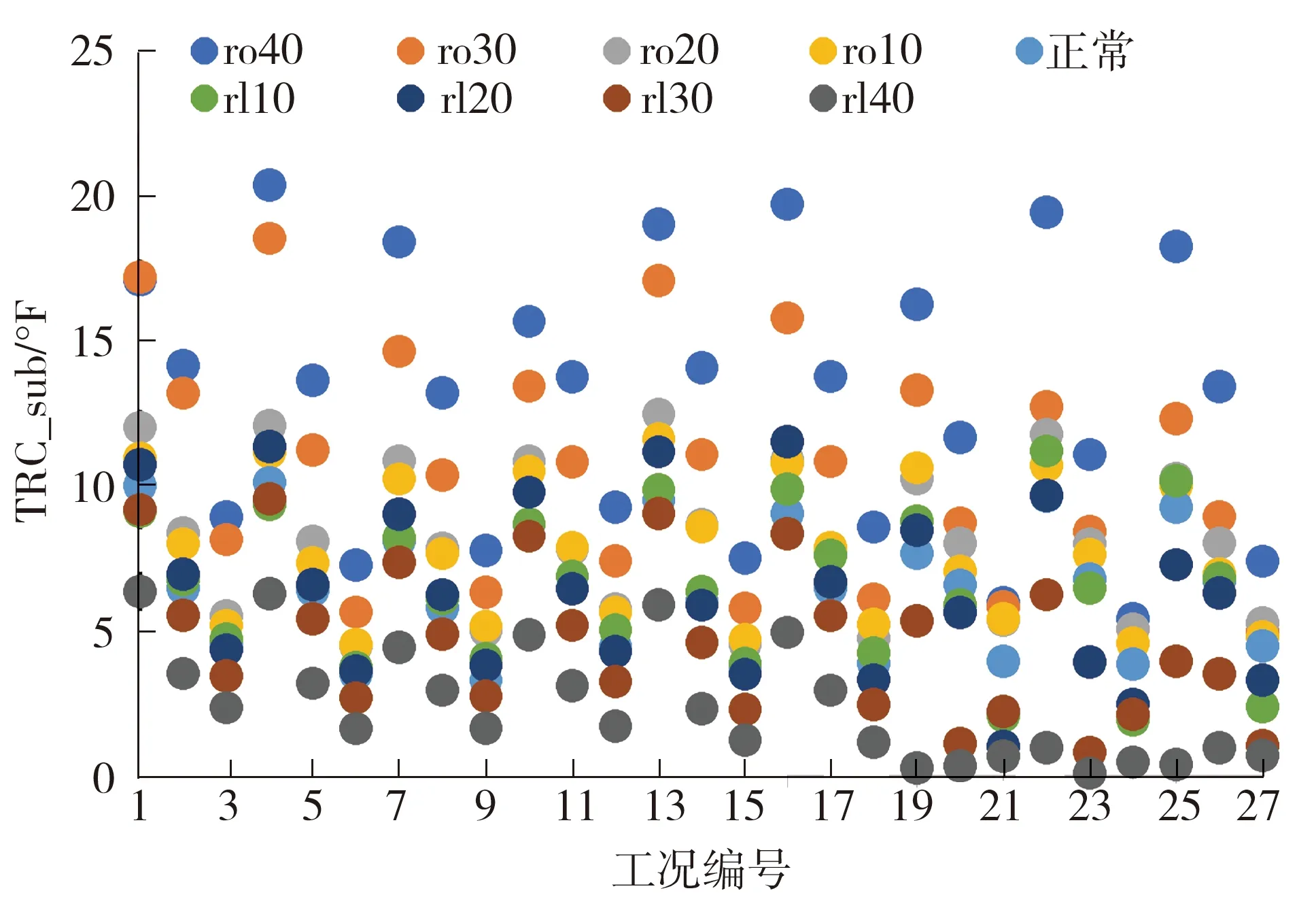
图6 27种工况下TRC_sub参数分布图

Fig.6 Distribution of TRC_sub parameter under 27 operating conditions

(3)TCA(冷凝器趋近温度)

冷凝器趋近温度是指制冷剂冷凝温度与冷却水出水温度的差值，表明换热器换热能力的参数。冷凝压力随着制冷剂充注量的增加而增加，冷凝温度与冷凝压力呈正相关。当制冷剂充注量过多时，制冷剂的换热量增加，导致冷却水温度降低，因此趋近温度升高；反之，趋近温度降低。图7为27种工况下不同制冷剂充注量的TCA分布图。由图中可以看出，同一工况下冷凝器趋近温度随着制冷剂充注量的减少而降低，相邻工况下TCA的分布有重合，需要结合其他参数对充注量进行诊断。

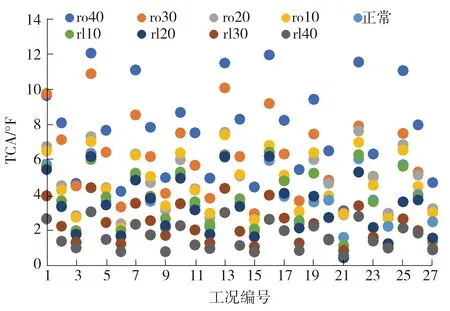
图7 27种工况下TCA参数分布图

Fig.7 Distribution of TCA parameter under 27 working conditions

3.4 故障诊断结果分析

故障诊断分类准确率可以有效地评价故障诊断方法的有效性。故障诊断准确率受到样本规模与故障特征量维度(DFCQ)的影响，因此文中以诊断准确率最高作为目标函数，比较不同样本规模与DFCQ在不同诊断方法的诊断结果，并对结果进行分析。

为了测试样本规模对模型故障诊断准确率的影响，分别选取4组不同的样本规模n(3 000、5 000、10 000、15 000)进行故障诊断，每组样本依据训练集和测试集3∶1的比例随机选取；同时依据贡献率大小，优先选用贡献率大的特征量，在逐渐增加DFCQ的输入条件下,分别采用基于RF、基于决策树(DT)、基于支持向量机(SVM)算法的制冷剂充注量故障监测与诊断方法进行故障诊断，这些方法的诊断性能受到算法参数的影响，文中采用网格搜索算法对RF、DT、SVM(采用RBF核函数)算法的关键参数进行寻优。首先以训练集准确度为评价指标，对训练集采用4折交叉验证方法，寻找算法的训练集最优参数值，然后将参数传递给相应的算法，并用测试集进行验证，寻优算法参数设置如表3所示，其中m∈min(15,DFCQ)。实验结果表明：3种方法的训练集准确率在99%～100%之间，如图8所示。3种方法的测试集5次实验的平均准确率如表4所示。

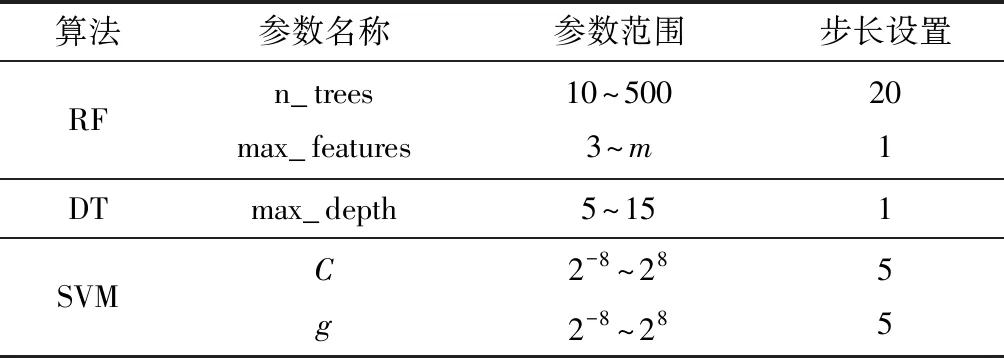
表3 寻优算法的参数设定Table 3 Parameter settings of optimizing algorithms

图8 3种方法的训练集准确率比较

Fig.8 Comparison of accuracy of training set among three methods

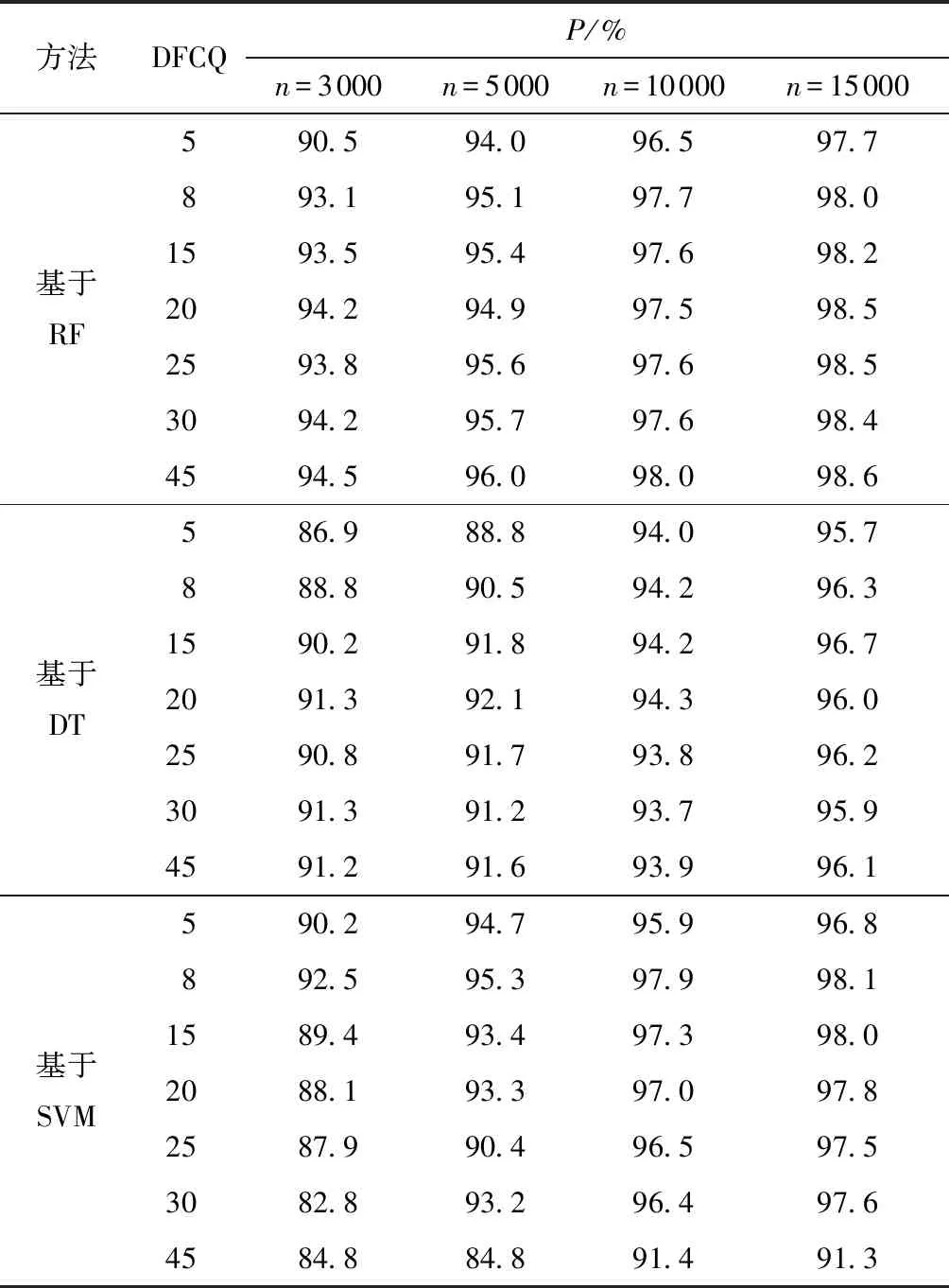
表4 3种方法的测试集诊断准确率比较

Table 4 Comparison of diagnosis accuracy of test set among three methods

方法DFCQP/%n=3000n=5000n=10000n=15000基于RF基于DT基于SVM590.594.096.597.7893.195.197.798.01593.595.497.698.22094.294.997.598.52593.895.697.698.53094.295.797.698.44594.596.098.098.6586.988.894.095.7888.890.594.296.31590.291.894.296.72091.392.194.396.02590.891.793.896.23091.391.293.795.94591.291.693.996.1590.294.795.996.8892.595.397.998.11589.493.497.398.02088.193.397.097.82587.990.496.597.53082.893.296.497.64584.884.891.491.3

由表4可知：基于RF算法的平均诊断准确率比基于DT算法高约3.3%，比基于SVM算法高约2.9%，说明RF算法的泛化能力最好；当DFCQ相同时，随着样本规模的增大，3种方法的诊断平均准确率呈上升趋势，但上升幅度逐渐变缓，说明增加样本规模可以提高模型诊断准确率，但当样本规模足够大时，模型诊断效果不能明显提升；当样本规模相同时，随着DFCQ的增加，基于RF算法的测试集诊断平均准确率升高且平均准确率最高约96.8%，基于DT算法的诊断方法在DFCQ为20时的平均准确率最高(约93.42%)，基于SVM算法的诊断方法在DFCQ为8时的平均准确率最高(约95.95%)，说明当DFCQ达到一定程度时，基于DT、基于SVM算法的诊断效果不会随着DFCQ的增加而增加，这是因为特征量维度过多导致冗余，会影响模型的泛化能力，导致模型过拟合，而基于RF算法的诊断方法的泛化能力相比基于其他两种算法的方法好，可以更好地解决模型过拟合和欠拟合问题。基于工程实践可行性的考虑，前5维的故障特征量都是典型的空调系统监测数据，基于RF算法、基于DT算法、基于SVM算法的平均准确率分别可以达到94.68%、91.35%、94.40%。在系统监测成本有限的条件下，采用RF算法，选取5维故障特征量可以实现制冷剂充注量的有效诊断。综合考虑模型平均准确率与监测成本时，采用RF算法可以实现制冷剂充注量的高准确率诊断。

4 结论

文中提出的异常诊断方法能够准确评估离心式冷水机组制冷剂充注量故障的严重程度，主要结论如下：

(1)通过故障特征量贡献率排序，有针对性地选取部分贡献率大的故障特征量进行诊断，可以在保留数据物理意义的条件下有效地减少数据采集成本;

(2)基于诊断准确率考虑，采用RF算法具有良好的识别分类准确率;

(3)基于工程实践可行性考虑，前5维的故障特征量都是典型的空调系统监测数据，采用RF算法可以实现制冷剂充注量的有效诊断;

(4)随机森林算法可以有效地处理规则模糊的数据，且该算法具有稳定性和普适性。

该方法能够为预防离心式冷水机组制冷剂泄露导致的火灾爆炸危害性事故发生提供有效依据，同时可预防因人为失误导致充注量过高而引发冷水机组液击事故的发生，以确保离心式冷水机组安全、稳定、高效运行。该方法也可为其他类型的冷水机组故障诊断提供参考。文中建立的故障诊断模型适用于各种型号的离心式冷水机组，但建模复杂度相对较大，今后可以尝试改进算法，以更好地实现故障诊断。