例谈几何题的命制方法

江苏省泰州市第二中学附属初中

命制试题的方法之一就是命题者从原有试题得到启发,对原有试题进行深度的改造,再加工,使之形式上有所改变、在原有考查知识点上进行拓展变化而编制成的创新题.由于是对原有试题的深挖掘,所以命制的试题一般都带有一定的新颖性和创造性.创新的方法很多,例如:改变设问角度、改变已知条件、改变考查目标、转换题型、题目重组等,一道好的创新题应当是既考查知识和能力又渗透数学思想,其核心是能够培养学生的核心素养.源自经典,传承创新是试题命制的常用途径.下面笔者从一道经典的几何问题出发,通过对近年来中考中出现的有关试题的分析,来了解其命题思路,感悟几何题的命制方法.

1 典型例题

如图1,正方形ABCD中,以A为顶点作∠EAF=45°,其两边分别交BC,DC于点E,F.求证:EF=BE+DF.

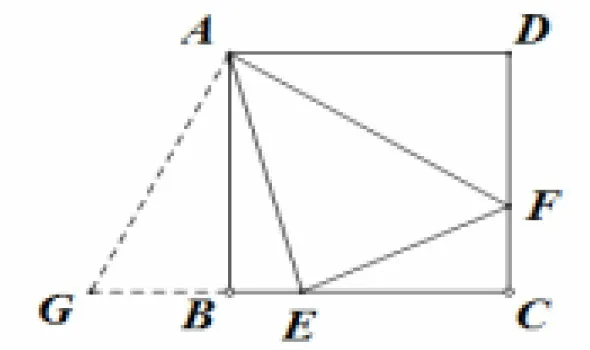
图1

分析:只要将ΔADF绕A点顺时针旋转90°,或用“补短”法在CB的延长线上取BG=DF即可.

1.1 引申结论

解题的过 程中,我 们 得 到 ΔABG∽= ΔADF,ΔAEG∽= ΔAEF.于是有

下面以此题为例,介绍几种常用的命制方法.

2 互换因果

把原题中的∠EAF= 45°与结论“EF=BE+DF”或结论1○之一,或2○,或3○,或4○互换得到五个新的命题.可以证明它们都是成立的.即上述六个性质中,只要其中一个成立,其余五个都成立.

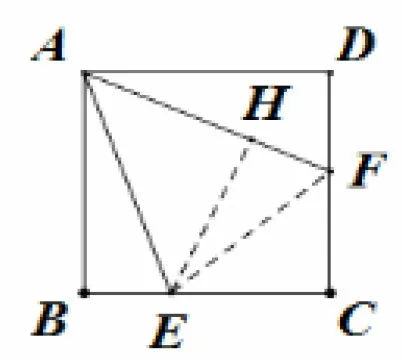
图2

例1如图2,正方形ABCD中,E为BC上一点,BE=为CD的中点.求证:∠EAF=45°.

思路(1)连结EF,设正方形边长为1,由勾股定理算得EF=再运用原题的分析中的方法.

思路(2)再作EH⊥AF,H为垂足,先算出EF,AF和AE的长,分别为再算出AH的长度.由可得.AH的长可通过如下方法得到:

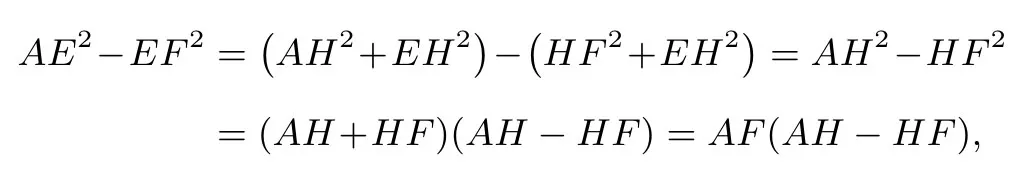
由方程组

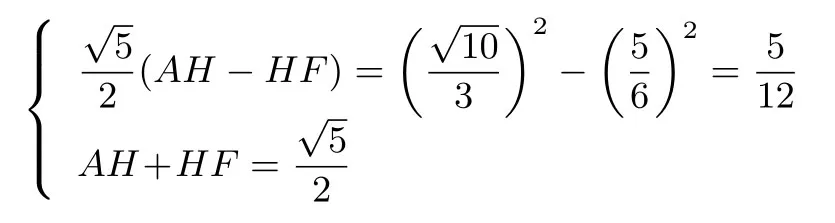
解得.

思路(3)如图3,由于F是CD的中点,则延长AF,BC得到交点M,易得CM=BC,再连接AC,得∠ACB= 45°.因此只要证ΔEAC∽= ΔEMA,通过计算可得

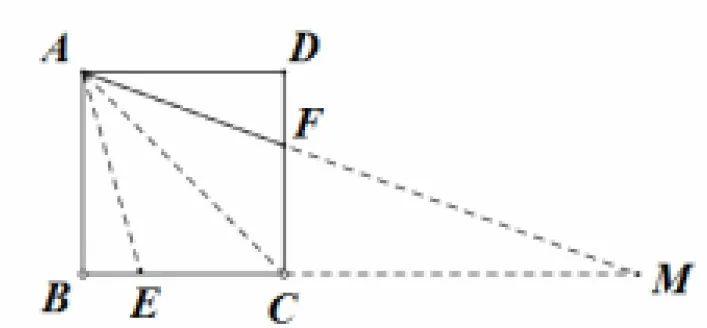
图3

3 变化点线

例2(2016年扬州市统考试题节选).如图4,已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕A旋转,角的两边与边BC、DC的延长线交与点E、F,设CE=a,CF=b.

(3)探索∠EAF绕点A旋转的过程中a,b满足的关系式(注:原题3问,只取第3问).

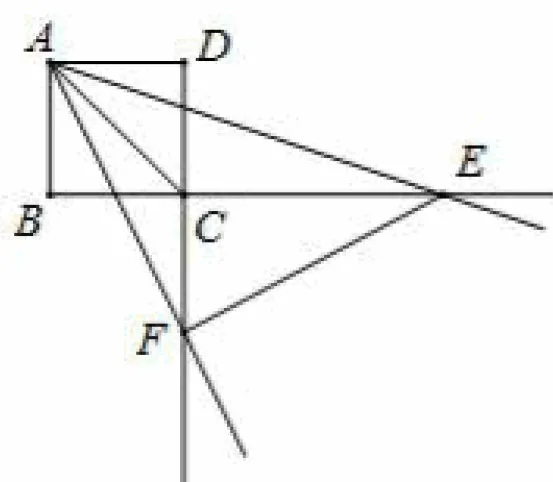
图4

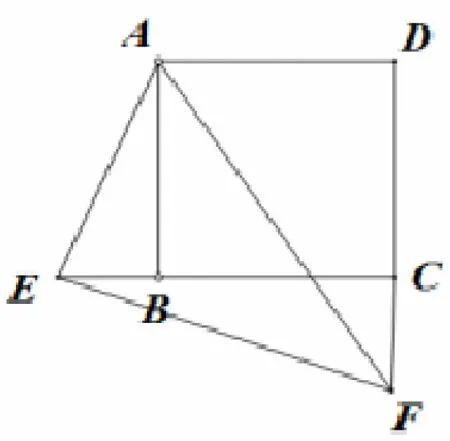
图5

分析本题与原题相比,只多了三个字“延长线”,即∠EAF与BC,CD的交点置于其延长上,研究的对象也发生了变化(不再是EF).因此,我们的思路也应随之改变,从例1的思路3 得到启示:可探索三角形相似.连接AC,则∠ACE=∠ACF=135°.证ΔCAE∽ΔCFA还缺一个条件.由∠CAE+∠CEA=∠ACB=45°=∠CAE+∠CAF,得∠CEA= ∠CAF,从而获证.于是有CE·CF=CA2=AB2+BC2=2×42=32.即ab=32.

如果把原题中的的两点E1、F1标上,还有ΔE1AC∽ΔE1EA,倘若把此题中“BC的延长线”改为“CB的延长线”,又可以得到新又有新的结论:EF=DF -BE.读者自证.

4 增改条件

例3 如图6在边长为3的正 方 形ABCD中,E是BC 边长的一个动点,作EP⊥AE,且EP=AE,交边CD于点F.

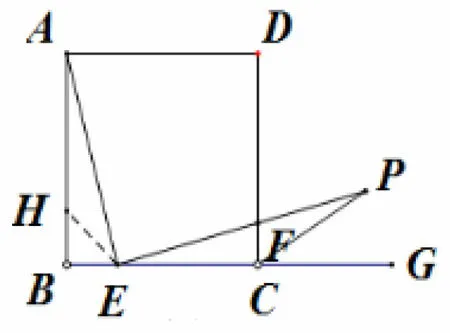
图6

(1)若BE= 1,求的值.(2)求证:∠PCG= 45°.(3)求DP的最小值.

思路(1)易知∠CEF= ∠BAE,ΔCEF∽ΔBAE,

(2)要证∠PCG= 45°,即证∠ECP= 135°.则要构造全等三角形.如果由“小补大”,以P作PG的垂线段则不能奏效,只有将“大”改“小”,在AB上取AH=EC,得ΔECP∽= ΔAHE,有∠ECP= ∠AHE,又由AB - AH=BC - EC得BH=BE,于是得出∠PCG=∠BHE=45°.

(3)由(2)知,不论P点怎样移动,它都在∠DCG的平分线上,因此DP的最小值应在DP⊥CP时取得(垂线段最短),此时ΔDCP为等腰直角三角形,DP=DC ·sin 45°=

5 寓形与数

例4如图7直线y=-x+1 与x轴交于点B,与y轴交于点A.M(a,b)为双曲线上的动点,MG⊥OA,G为垂足,交AB于F,MH⊥OA,H为垂足,交AB于E.

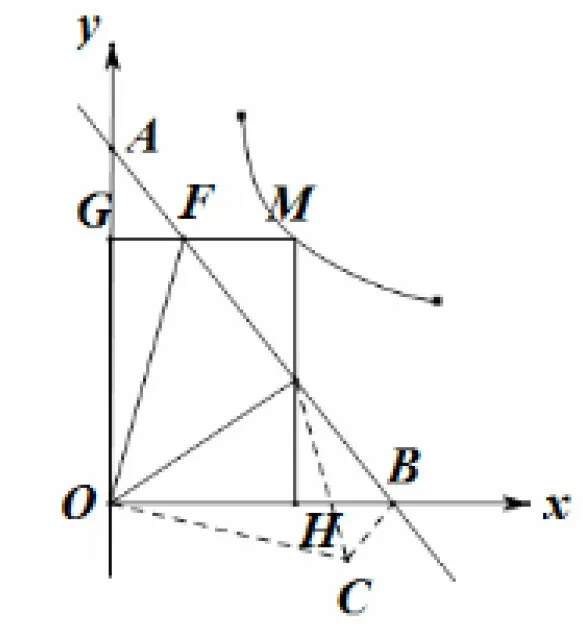
图7

求证:(1)S矩形OGMH=SΔOAB;

(2)∠EOF=45°.

分析(1)易得A(0,1),B(0,即ab= 1,ΔAOB是等腰直角三角形,OA=OB= 1,MG · MH= 1,即

(2)证明思路是在直角平面坐标系中利用数形结合的解题方法,求出有关线段,再应用相似三角形求证;另一个思路是运用问题(1)寻求突破.

证法(1)注意到ΔAGF,ΔMEF,ΔBEH都是等腰直角三角形,则E(a,1-a),F(1-b,b),(因ab==a2+ (1- a)2=OE2.因为所以ΔEOF∽ΔEAO,∠EOF=∠EAO=45°.

证法(2)将ΔAOF顺时针旋转90°至ΔBOC,连结EC,则BC=AF,由(1)得SΔMEF=SΔAGF+SΔBEH,即就是EF2=AF2+BE2.而在RtΔEBC中,EC2=BC2+BE2,得EC=EF

在ΔEOF和ΔEOC中:EF=EC,OE=OE,OF=OC,则ΔEOF∽= ΔEOC,有∠EOF= ∠EOC=

6 类比联想

例5 如图8,菱形ABCD中,∠BAD= 120°,以A为顶点,作角分别交BC于点E,交CD于点F.

(1)求证:ΔAEF为等边三角形.

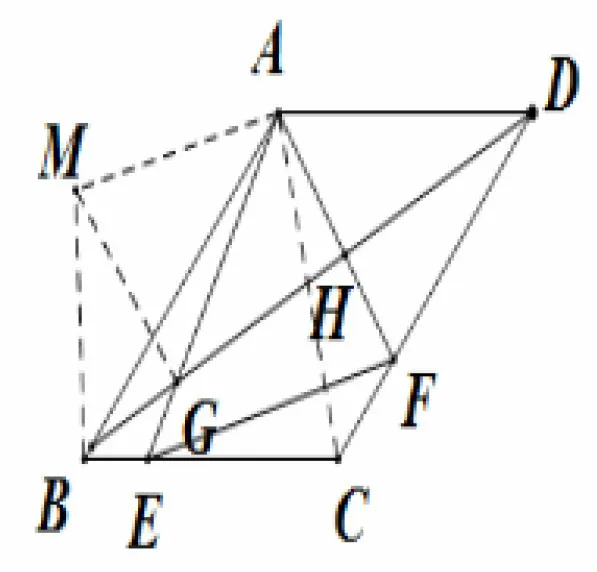
图8

(2)连BD,分别交AE于点G,交AF于点H,若∠BAG= 15°,试判别这三条线段所构成的三角形的形状.

思路(1)只要证AE=AF,连接AC,得∠ABC=60°,ΔABC是等边三角形,由此易证ΔABE∽= ΔACF. (2)将ΔADH 绕点A 顺时针旋转120°至ΔABM,则∠BAM = ∠DAH = 120°-60°-15°=45°,∠GAM = 45°+ 15°= 60°= ∠GAH,再由AH =AM,AG是公共边又得ΔAGM ∽= ΔAGH,∠AGM =∠AGH = ∠BAG+∠ABG = 15°+ 30°= 45°.于是MG⊥GH,ΔBMG是直角三角形.

我们对照原题,本题于原题都有以下共同点:“以某角的顶点为顶点作一个角等于它的一半”其实如果把正方形改成菱形或改成顶角为120°的等腰三角形,也会得到和上面题型类似的结论,同样可以命制出新的试题.

回归经典就是重要的命题方法,命制时厘清经典试题的条件结论,对结论和条件进行深度的改编和重组,在注重试题梯度的情况下,注重拓展,以达到既考察学生基础知识,又考察学生综合运用数学知识的能力,就能命制一道新颖别致的创新题.