数学复习中,高三学生磨道效应的成因及破解

广东省阳江市第一中学

在现行的人才选拔制度下,高考是一种相对比较公平的人才选拔模式,每年全国都有几百万的学生参加高考.不管高考备考是备三年,还是六年,高三的备考一定是战略的重点,所以高三复习的重要性就无需赘述.然而,在高三的数学复习中,不少学生却陷入简单地模仿和机械地重复解题的怪圈中,虽然这部分学生每天一睁眼就解数学题,一闭眼还解数学题,但成绩却是“涛声依旧”,这就是出现了心理学上的磨道效应.学生磨道效应的出现对于复习计划的落实和复习效果的达成都将会有重要的负面影响,所以认知高三学生磨道效应的表征、明确磨道效应的成因和探寻破解的对策就显得非常必要了.

1 学生磨道效应出现的表征

磨道效应取材于驴子拉石磨的现象,被石磨拴着的驴子看似走了很久,走了很长的路,但依旧在“原地转圈”.心理学上用磨道效应来概括某些主体在工作过程中陷入了简单重复的怪圈的现象.出现磨道效应的人,路走了很多,却一直在原地打转,实际并没有走出很远,自身的素质并没有得到长足的提高.不少学生在数学复习中,有这样的现象:每天很忙碌,从早到晚都在做数学题,但数学成绩却不见提高.这部分学生已陷入了磨道效应的怪圈.

2 学生磨道效应形成的原因

2.1 在数学复习中,只重视知识结论的应用而忽视知识的形成过程是使学生陷入磨道效应怪圈的第一个原因.

由于高三要复习的内容很多,而时间很短,所以不少学生有急攻近利的思想.在数学学习的过程中,不少学生只记住老师所教知识的结论而忽略该知识生成的过程.由于对数学知识的来源不理解,所以很容易忘记.于是就通过大量的练习来“保温”,美其名曰“加深理解”,实际上是陷入了磨道效应的怪圈.

2.2 在数学复习中,重视模仿例题的解题方法而忽视解题后总结反思是使学生陷入磨道效应怪圈的第二个原因.

在课堂上,老师一般都会通过典型的例题讲解基本的解题思路和基本解题方法等.不少学生在此时就会拼命的抄笔记,怕错过了老师写的每一个符号,而不是认真听老师分析如何解答、为什么会这样解答等,更没时间向老师提出自己的困惑和与老师交流自己的不同想法.课后就进行大量的模仿练习,美其名曰“巩固提高”,实际上已经在不知不觉中陷入了磨道效应的怪圈.

2.3 在数学复习中,重视解题的数量而忽视题目的质量是使学生陷入磨道效应怪圈的第三个原因.

每个高三学生的手头至少有三千道数学题,要想把这些题做完了再参加高考,那每天得做100 道左右的数学题.如果只顾数量而不加选择的话,只会让自己的学习效率更低,甚至是做无用功.学生在“勤奋”的漂亮外衣下不知不觉中陷入了磨道效应的怪圈.

3 学生磨道效应的破解策略

要想破解这个磨道效应的怪圈,需要各方面的努力.而教师作为教学的引导者和组织者,更是在其中起到关键的作用.教师不仅在课堂上要引导学生参与知识的形成过程,指导学生学会解题后总结反思,还要组织班级学习小组和调动家长的积极性,请家长配合老师的工作.

3.1 教师在课堂上引导学生参与数学知识的形成过程,引领学生走出磨道效应的怪圈.

教师在课堂上不但要将知识存在的背景、生成过程及应用等来龙去脉讲清楚,还要让学生参与其中,这样能更好地加深学生的理解和记忆,也能更有效地引领学生走出磨道效应的怪圈.比如:

题目 (2015年新课标Ⅰ卷(文科)第16题)已知F是双曲线C的右焦点,P是C 左支上一点,当ΔAPF 周长最小时,该三角形的面积为____.

这是一道难度较大的题目,不少学生感到无从下手.

师:这道题的知识载体是什么?

生:双曲线.

师:求解的目标是什么?

生:求三角形的面积.

师:双曲线与三角形的关系如何体现?

生:可以通过图形体现它们的联系.

师:好！请你们把图像画出来.(稍等一会)

师:三角形是固定的吗?

生:不是.点A,F是定点,点P是双曲线左支上的动点.

师:很好！要想求ΔAPF的面积,关键是要确定点P的位置.点P 应满足什么条件呢?

生:点P 使ΔAPF的周长最小.

生:ΔAPF的周长为|AF|+|AP|+|PF|=15+|AP|+|PF|,也就是要|AP|+|PF|取最小值.

师:如何求|AP|+|PF|的最小值?

生:_______设点 P(x0,y0),求 |AP| + |PF| =的最小值.但求不了.

师:代数法思路受阻.回头想一想|AP|+|PF|存在的背景是什么?

生:三角形的两边之和.

生:哦！三角形的两边之和大于第三边,|AP|+|PF| ＞|AF|.(惊喜)

师:很好(鼓励一下).但我们要求最小值,取到最小值|AF|吗?

生:不能.

师:为什么?

生:点P 不在线段AF 上.

师:怎么办呢? 多好的思路呀！(鼓励一下,坚定下信念)

师:能不能把|AP|+|PF|作等价转换,使得点P 在某线段上呢? 想下我们这道题的知识背景?

生:可以用双曲线的定义进行等价转换.设双曲线的左焦点为F′,|AP|+|PF| = 17+|AP|+|PF′|,转化为求

师:很好.

生:老师,可以了,|AP|+|PF′| ≥|AF′|,当且仅当点P在线段FA′时等号成立.

师:恭喜了,你们太厉害了,能求ΔAPF的面积了吗?

生:可以了.

师:回头反思下我们的解题思路,用到了什么数学思想和方法解题呢?

生:数形结合思想、等价转化思想.

师:很好.恭喜你们会用这两种数学思想解题了.

以数学知识为载体,让学生参与数学思想和方法的形成,可以加深对数学思想和方法的理解,培养学生数学思维,提升分析和解决问题的能力,引领学生走出磨道效应的怪圈.

3.2 老师指导学生做好解题后的总结与反思,养成良好的解题习惯,让学生自己走出磨道效应的怪圈.

不少学生在解题时是“解而不思”,即没有养成解题后总结反思的良好学习习惯.老师除了提醒学生解完题后要总结反思外,更重要的是要指导学生如何进行总结反思.

比如指导学生解题后要进行“三思”:一思:解题过程是否正确.即在解题后要反思为什么要这样做、这样做正确吗、这样做的关键是什么、为什么不能那样做、那样做行不通的原因是什么等.二思:解题方法是否最好.即反思除了这个解法外,是否还有别的解法呢,这解法是否是最优的呢等.三思:这个方法是否适用于其他题目呢,若将原题变一变是否还适用呢等.例如:

若对任意x ≥2,不等式x2-(1+a)x+2a+2 ≥0 都成立,则实数a的取值范围是____.

解1由Δ=(1+a)2-4(2a+2)≤0 得:-1 ≤a ≤7.

解2令f(x)= x2- (1+a)x+2a+2,则不等式x2-(0+a)x+2a+2 ≥0 对任何x ∈[2,+∞)恒成立⇔函数y = f(x)的图像在x轴的上方⇔函数y = f(x)在[2,+∞)的最小值大于或等于0 ⇔

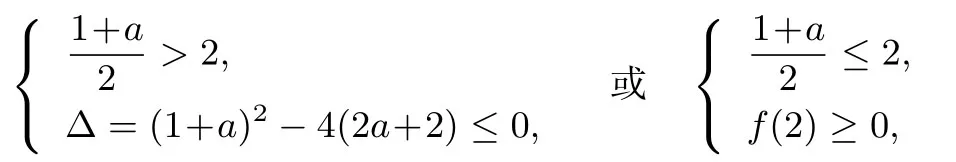
解得:a ≤7.

指导学生反思如下:

反思一解1是错误的,因为该一元二次不等式是对任意x ∈ [2,+∞)成立,而不是x ∈ R,所以函数f(x)= x2- (1+a)x+2a+2的最小值不一定在顶点处取到.

解2是正确的,该题可转化为研究函数f(x)=x2-(1+a)x+2a+2 在[2,+∞)的最小值,二次函数对称轴的位置不同,函数y = f(x)在不同的位置取得最小值,于是可用分类讨论的方法研究最小值.

反思二另解3:x2-(1+a)x+2a+2 ≥0 ⇔a(x-2)≤

对任意x ＞2, 不等式x2- (1+a)x+2a+2 ≥0 都成立, 即令当且仅当即=4 时等号成立. 所以y =g(x)的最小值为7,故a ≤7.

综上:a ≤7.

比较解2 与解3,两种方法的共同点是:将不等式恒成立问题转化为研究函数的最值问题,不同的是解2 研究二次函数的最值,解3 采用参变量分离的方法研究分式函数的最值.

反思三解2、解3的方法是否还适用于其他的不等式恒成立问题呢? 如:

配套练习(1)若对任意a ∈[-2,2],不等式x2-(1+a)x+2a+2 ≥0 都成立,求实数x的取值范围.

解题后总结反思不仅能够提高学习效果、培养学习能力,更重要的是可以培养思维的深刻性、广阔性、批判性和创造性等品质.让学生自己走出磨道效应的怪圈.

3.3 教师组织好班级学习小组,让学生在同学的帮扶带作用下走出磨道效应的怪圈.

在学校,同学间的相互影响是巨大的,所谓“近朱者赤,近墨者黑“就是这个道理.充分利用这个影响,有意识地分学习小组,可以让学生在同学的帮扶带作用下走出磨道效应的怪圈.比如:

教师先深入了解班上的每一位学生的学习习惯、方法等,将学习习惯、方法较好的学生分为第一类,已经走入或将有可能走入磨道效应怪圈的学生作为第二类.教师将4-6人分作一个学习小组,每个小组内都有上述两类学生,并且比例要适当.学习小组内的每一个学生都有自己的工作任务,都有一个职位名称,比如:学习小组长、记录员、检察员、汇报员等等,让组员明白每个职位的职责.比如汇报员可以是专门将小组研究出的解题方法、心得等向全体学生汇报,这项工作就可以有意识地让第二类的学生完成,让他们在汇报的过程中学习、消化其他同学好的学习方法、思维习惯等,让第二类学生在同学的帮扶带作用下走出磨道效应的怪圈.当然各项工作要适当轮换,使更多的学生学习到更多的知识.

3.4 教师调动家长的积极性,请家长配合教师的教学工作,帮助学生走出磨道路效应的怪圈.

在高考备考中,说家长的心态决定孩子的状态一点都不为过,因为从小到大,家长就是孩子的第一任老师,所以家长的一言一行都对孩子有莫大的影响.老师如果能与家长多沟通,在家长心态的调整、做法等方面上,根据不同的家庭背景,给不同的建议.借助家长的力量,在让孩子走出磨道路效应的怪圈上往往能收到意想不到的效果.

要让学生在高考备考中不原地转圈,而是走得更远、更好、更有效,这需要老师的力量,但同时也需要学生自己和家长等各方面的力量,只有在各方面的力量合到一处,才能让学生走出磨道路效应的怪圈,才能让每一个学生都像野白合一样,拥有自己的春天.