智慧灵动课堂探究—-一节高三试卷讲评课精彩核心片段实录及反思

广东省佛山市顺德区北滘镇莘村中学

题目在直角坐标系xoy中,直线l的参数方程为:(t为参数),以坐标原点O为极点,x轴的正半轴建立极坐标系,曲线C的极坐标方程为:

(1)求曲线C的直角坐标方程与直线l的普通方程;

课堂实录

课堂上,学生甲用2分钟左右在一体机板书完毕,(学生展示的答案与标准答案差不多)接下来是学生自我点评、师生对话片段.

学生甲:第(1)问比较容易,我就不再点评.(听到这句话,老师微微一笑,并没有打断该同学)现在请大家一起来看看第(2)问,第二问的难点是写出新的直线参数方程的“标准”形式:即直线l的参数方程为:(t为参数),将其代入圆的普通方程,再利用“套路”,即化为关于t的一元二次方程,再利用韦达定理解决.

师曰:展示得非常好,讲评也非常到位.现在老师问你几个问题.

学生甲:因为原直线的参数不经过点P,不符合“套路”.

教师听完后,点了点头,继续追问,

师问2:这两个参数方程本质一样吗?

学生甲:略微思考答,一样,都是表示同一条直线,只不过选定的点不同.

师问3:这条直线的斜率是什么?可以快速确定吗?

师继续追问.

师问4:能够从参数方程本身,快速“看”出斜率呢?

学生甲:······

见到学生答不上来,教师提示了一下学生思考参数方程的标准形式的特征,这时台下有同学说,可以利用倾斜角快速判断.学生甲恍然大悟,继续回答,

教师表扬了一下该同学,并示意该同学留在台上,继续追问:

学生甲:······

学生很迷惑地看着老师,不得其解,教师只好继续引导,师曰:实际上直线l的参数方程

这时学生甲彻底“断片”了,不过台下有部分学生反应过了,帮她做了回答:不是.

教师继续追问,

师问6:为什么不是呢?

教师伸出大拇指,表扬了下台下的同学,继续追问:

师问7:如果你是老师,还可以如何改编这道题呢?

这时立即有个同学举手回答了:老师,我觉得可以把条件中直线l的参数方程为:(t为参数)修改为:(t为参数),这样解题时必须先把这个式子转为标准形式.这时全班同学如有所悟,纷纷点头.

师曰:非常好.实际上,老师翻阅了下你们的答卷,绝大部分学生(包括学生甲)是直接将题干中的直线l的参数方程代入化简求解的,从而导致后面几乎没有得到分数.学生甲功底不错,很快就根据出错的问题很快就纠正了过来,说明一轮复习下来,她的基础知识比较牢固,但是缺陷也是有的,那就是解题能力还有待提升,对问题没有深入归纳和总结,这也正是我们二轮复习的重点,即提升学生的解题能力、拓展学生的解题视野.

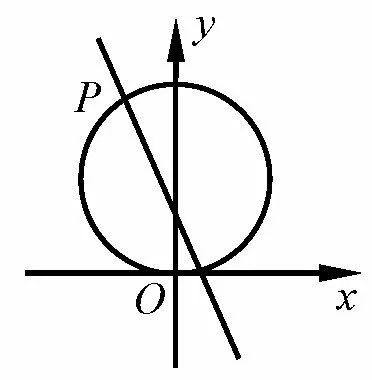
图1

看到同学们所有所思地点点头,教师继续因势利导,值得高兴和遗憾的是,这个同学解题懂得了“套路”,却忽略问题本质的思考和探究.实际上,若我们画出图形是有机会弥补这个致命缺陷的,但这个同学用了套路以为图也就那样,白白失去了一个“自我救赎”的机会.大家来看看这个图,教师随手快速画出了草图.

师曰:由图1可知,点P 显然在圆的内部,所以根据直线的参数方程的几何意义,t1,t2的值异号,而根据大部分同学的解法:

这显然与参数t的几何意义不符合,可以促使我们回过头检查下问题所在.这时候大部分同学包括在台上的甲同学都彻底明白了,这个教育片段也可以说取得了一定的成功.

这个教学片断因为教师在课堂上设置了比较好的铺垫,恰到好处的问题,不断地追问,帮助学生一步步追寻问题的“真相”,所幸的是教师充当的只是一个导演,至始至终没有代越庖俎,就算是最为“惊险”的地方也是想法让学生自行探究和感悟,就像带领学生坐在游乐场过山车的车厢上,亲自感受,自然印象深刻,笔者认为这个片段的精彩之处在于教师的“逼问”和思维的碰撞,整个过程只有十分钟不到,却也能一气呵成,学生也有所收获.这个片段与真正“智慧灵动”课堂还有一定的差距,请读者诸君批评指正.

一节课也好,一个成功的教育片段也好,上得再好,如果课外不巩固,对于数学而言也是伤不起的,就像再精彩的广告,虽然能够当场吸引住人,但是过后大都会忘记,至少不会对其进行深入思考,更遑论总结升华呢? 授人以鱼不如授人以渔.

补充练习

(1)求直线的普通方程;

(2)化参数方程为标准形式.

A.30°B.60°C.-45°D.135°

(1)求圆C的直角坐标方程;

(2)设圆C 与直线l 交于点A,B,若点P的坐标为(1,2),求|PA|+|PB|的最小值.

C的交点为A,B,设M为弦AB的中点.(1)已知P(1,4),求|MP|;

(2)若P(x,y)在曲线C 上,求ΔABP的面积最大值并求出此时的点P 坐标.

参考答案1.(1)4x + 3y - 50 = 0; (2)(t为参数).2.D.3.(1)x2+(y-3)2=9;点P的坐标