串“问”为“链”,让数学问题绽放光彩*—-初中数学课堂中的“问题链”设置

江苏省海门市东洲国际学校

问题是课堂中不可或缺的重要元素,它承载着知识与能力,问题的质量直接决定着教学质量.数学是一门较为“质朴”的学科,没有太多的式样,大部分知识是在教师的引导下学生探究得到,相对于其他学科,数学课的问题也是最多的.在强调学生自主学习的当下,教师充分而不过分的引导显得尤为重要,在教学中精心设置“问题链”可以作为引导学生自主学习的方式之一.问题链是教师在课堂教学中根据教学目标、围绕教学内容所设置的问题群,既包含教师预设的问题,也包含教师根据实际教学情境临场提出的问题,这些问题层层深入、步步递进、环环相扣,犹如一条锁链贯穿课堂,将教学内容串联成整体.问题链得的设置体现出了教师对知识引导的方式及引导的深度,那么如何设置问题链才能即利于提高学生的主动学习能力,又能激发学生的学习动机? 在实践与思考中,笔者觉得可以从以下几个方面进行尝试,下文结合实际谈一谈:

1 提问视角,引入教学

提问,顾名思义就是直接提出问题,通常是由教师预设的,因此对于问题链中的每个问题教师都可以仔细斟酌并取舍.

以新授课为例,在引入环节以提问的方式设置问题链可以让学生通过思考获知本节课学习的内容,从而对本节课的内容产生兴趣及期待.如在新授课《15.1从分数到分式》(人教版,下同)中的引入环节,可以设置如下问题链:

问题1星期天到了,小明骑车去敬老院进行社会实践,路上共用了21 min,已知敬老院离家3500 m,则小明的速度为____min/m.

问题2到了敬老院,小明把妈妈在家精心熬制的五谷杂粮粥分发给部分老人,已知粥的总量是6 L,正好分了m 碗,则每个碗的容积约为____L.

问题3为了响应班级中“环保”的社会实践主题,小明利用多个回收的包装盒子给老人们制作成了一个精美的长方体杂物收纳筐,已知该收纳筐的体积是9 dm3,底面积是S dm2,则它的高为____dm.

问题4从敬老院出来,小明想骑车去外婆家看望外公外婆,已知他骑车的速度不变,外婆家到敬老院的距离为a m,则他需要____min可以到外婆家.

问题5上面的式子有什么特点? 它们都是我们所熟悉的代数式吗?

问题6如果让你对上述式子进行分类,你怎么分? 你依据的分类标准是什么?

上述的问题中的前四个问题从一个贴合学生生活的背景展开,自然过渡,可以引起学生的注意,激发兴趣,后两个问题各包含两个小问题,逐个递进,展现教学内容,引入教学.从直接提问的视角设置问题链是最常见也是运用频率最高的,教师的关注点应置于问题的价值和问题的深度上.

2 反问视角,举一反三

反问就是用疑问的形式表达确定的意思,也就是“无疑而问”.通常是由教师在学生回答完问题或者解决完问题之后提出的,这些问题更多地偏向于自然生成,无法预设.在教学中从反问视角设置问题链可以强化学生对知识的印象,加深学生对知识的理解.

九年级上册“一元二次方程的解法—公式法(2)”的习题课中,根据方程解的个数确定方程中参数的取值范围是重点内容,也是难点,学生错误率较高.

如:已知关于x的一元二次方程nx2-(2n+1)x+2=0有两个不相等的实数根,求n的取值范围.

大部分学生的解答过程如下:Δ = (2n+1)2-8n =4n2+4n+1-8n=(2n-1)2＞0,所以

上述解答过程缺少了对二次项系数不为0的考虑,答案是错误的.此时如果教师直接告知学生错误原因并让学生改正显然效果不佳,可以尝试以反问的方式设置如下问题链:

问题1我们知道根的判别式是适用于什么方程的?

生:一元二次方程.

问题2如果方程不是一元二次方程能不能用呢?

众生摇头.

问题3那如何保证一个方程是一元二次方程呢?

生:含有一个未知数,未知数的最高项次数为2.

问题4怎样用式子来表示?

生:ax2+bx+c=0(a/=0).

问题5怎么保证题中的nx2-(2n+1)x+2=0 就是一元二次方程?

生:n/=0.

问题6如果去掉题干中的“一元二次”四个字,所得结果还一样吗?

上述几个问题中,问题1和问题2 其实是“明知故问”的,答案非常明显地存在于问题中,学生也许会对这两个简单问题的用意感到疑惑,但是第三个问题就明显地指向于题目的中心.问题4和问题5 实教师根据学生的回答及反应情况自然生成的,目的是将学生的注意引入到该实际问题中.问题6是对该问题的延伸,让学生用举一反三的方式加深对该问题的理解.从狭义上来说,反问就是从问题的反面进行提问,即从另一个角度思考问题,因此它不仅可以加深学生对问题的认识,而且也有利于发散学生的思维.

3 设问视角,发展思维

设问就是通过一些情境或者设置一些问题让学生对所学习的内容产生兴趣或者对所要解决的问题产生探究欲望,同时也能让学生在学习中提高质疑能力.从设问的视角设计问题链,可以引领学生思考问题的正确方向,找准思路、发展思维.如在初三复习课中,题目常常会充斥课堂的主要时间,通过适量题目的训练来总结方法、提高能力是数学学科上较为有效的方式.对于大部分学生无法独立解决的问题,教师的引导是必须的.如何引导才能恰到好处地让学生学会了知识、提高了能力?问题链有着较为明显的优势.

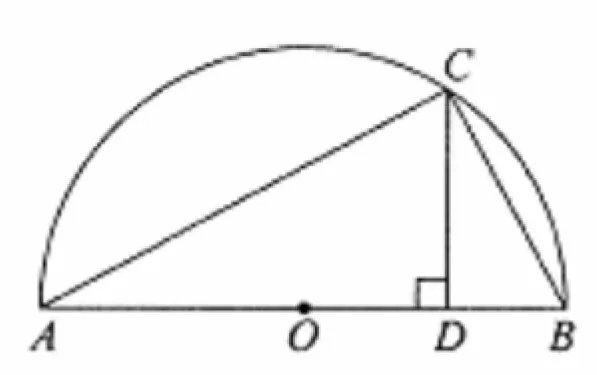
图1

如图1,在圆心为O,直径为AB的半圆中有一个动点C(不与BA,重合),过点C作AB⊥CD于点D.已知AB = 8,如果假设AC为x,AD为y,试求x-y的最大值.

问题1题目中要求x-y的最大值,那么x-y的值能在图形中表示或体现出吗?

众生摇头.

问题2x-y是两条线段的差,为什么无法在图形中体现出来?

生:因为这两条线段的长度都是不定的.

问题3那这两条线段的是一起动的吗? 它们之间是否存在某些联系呢?

生:是一起动的,AC的变化会导致AD的变化.

问题4既然两条线段存在联系,能不能找到它们彼此间的联系呢?

生(思索并演算后回答):由图可知ΔABC ∽ΔACD,则即所以y可以表示成可以转化成

问题5的最大值应该往哪个方向去思考呢?

生:二次函数的最值.

学生感到这个问题难以解决的原因在于无法对yx-进行转化,上述5个问题层层递进,每个问题都能引发学生的思考,自然将学生的思维逐渐向函数角度引领,第5个问题之后题目并没有完全解决,但是教师已经无需再继续参与,学生随即可以自行解决.教师扮演了引导者的角色,解决问题的主角依据是学生.通过这样的一串问题链,学生知道了思考问题的方向,通过对“跳一跳,够得到”的问题的思考,思维也得到了锻炼.

设问就是为了强调某一部分的内容而故意提出的问题,通俗来讲就是“明知故问,自问自答”.而学生的学习也正是在这些看似简单的问题中自然发生的,学生的思维也是在这些逐渐深入的问题中得到发展与提高.

“教”是教师的主要任务,如何教、教什么是教师所关注的,往具体来说,教的关键就是对问题的设置.问题链的设置不仅需要定位问题的难度,更要注重问题与问题之间的联系,只有将零碎的问题串联成“链”,才能让每个问题发挥作用,绽放光彩.