关于一类数字半群的Frobenius问题
吴 琳,孙广人,凌 燕,潘 萍
(安庆师范大学数学与计算科学学院,安徽安庆246133)
19世纪末,德国数学家Frobenius根据硬币问题提出了著名的Frobenius问题:给定一组正整数系数l1,l2,…,lp( p ∈ℤ+),求出使不定方程Y =l1x1+l2x2+…+lpxp没有非负整数解的最大正整数Y。这个最大正整数Y则称为相对于l1,l2,…,lp的Frobenius数。同时,Frobenius还证明了当方程系数l1,l2,…,lp的最大公约数等于1时,Frobenius数就一定存在。之后,随着Frobenius问题研究的深入,进而产生了数字半群这一新概念。
下面给出数字半群的基本概念[1]。令ℕ是所有非负整数构成的集合,若ℕ的子集S在加法下封闭,0 ∈S且ℕS有限,则称S是数字半群。给定ℕ的一个非空子集A,用A 表示由A生成的( )ℕ,+ 的一个幺子半群,即

此外,A 为数字半群当且仅当集合A中的所有元素的最大公约数为1。对于数字半群S,若S满足条件S= A ,则称A是S的生成元系,集合A中的元素称为S的生成元;若A的任意真子集都不能生成S,则称A是S的极小生成元系。每个数字半群S都有唯一的一个极小生成元系并且这个极小生成元系中的元素个数也都是有限的,也就是说每个数字半群都是有限生成的[2],数字半群S的极小生成元系中的元素个数称为S的嵌入维数,用e( )S 表示;对于不能用数字半群的极小生成元系线性表示的最大正整数,即不属于S的最大正整数,称为数字半群S的Frobenius数,用F(S) 表示。由此可知,Frobenius问题的数字半群形式为给定数字半群的一组生成元,求出只和生成元系有关的F(S)计算公式。数字半群的Frobenius问题是一个经典问题[3-7]。目前,嵌入维数为2的数字半群Frobenius问题及许多相关问题已经得到了解决[8]。但是,对于嵌入维数不小于3的数字半群,这些问题都是N-P问题[9],因此一些特殊数列生成的数字半群一直是研究热点[2,10-11]。
对于固定的n ∈ℕ,Thabit数字半群T( n )是由数列3·2n+i-1( i ∈ℕ )生成的,若将数列通项公式中的系数3变成任意的一个奇数2m-1(m ∈ℕ且m ≥1),此时新的数列( 2m-1 )·2n+i-1( i ∈ℕ )生成的数字半群就是数字半群T( m,n )[12]。文献[12]中已经确定了T( m,n )的极小生成元系并且求出了Frobenius数的计算公式,解决了T( m,n )的Frobenius问题,而本文将对数字半群T( m,n )更加一般的数字半群继续研究同样的问题。对于固定的n ∈ℕ,m ∈ℕ 且m ≥1,将数列( 2m-1 )·2n+i-1( i ∈ℕ )系数中的1 变成任意的奇数k并且规定1≤k <2m-1,这时生成的数字半群为T( m,k,n )=通过一系列的归纳论证探究了新数字半群T( m,k,n )的极小生成元系,嵌入维数和Apéry集等方面的性质,又针对k=2m-1 和k=2t-1(t ∈ℕ 且t ≥1)这两种特殊情况,研究了T( m,k,n )的Frobenius 数,求出了这两种情况下的数字半群T( m,k,n )的Frobenius数计算公式。
1 嵌入维数e( T( m,k,n))
令m,n为两个正整数且2 ≤m ≤2n,令k是奇数且1≤k <2m-1,则

引理1[12]令S是由非空集合A生成的数字半群,则下列条件等价:
(1)∀a ∈A,2a+1∈S;(2)∀s ∈S{ 0 },2s+1∈S。
在引理1的基础上可以得到下面的结论。
引理2 若m,k,n ∈ℕ,2 ≤m ≤2n,k为奇数且1≤k <2m-1,则T( m,k,n )=
证 明 令S′= { s0,s1,…,sn+m-1},显 然S′⊆T( m,k,n )。接 下 来 要 证 明T( m,k,n )⊆S′,若i ∈{ 0,1,…,n+m-2 },则2si+1=si+1∈S′。对于i=n+m-1,有

根据引理1,可得对于∀s′∈S′{ 0}(这里用s′表示数字半群S′中的任意一个元素),有2s′+1∈S′。
综上可得,对于i ≥m,有sn+i∈S′,即T( m,k,n )⊆S′。同时可知{ s0,s1,…,sn+m-1}是数字半群T( m,n,k )的生成元系,下面在此基础上证明{ s0,s1,…,sn+m-1}是T( m,k,n )的极小生成元系。
引理3 若m,k,n ∈ℕ,2 ≤m ≤2n,k为奇数且1≤k <2m-1,则sn+m-1∉
证明 证明方法过程与文献[12]中引理2.3相同。
根据引理3确定了T( m,k,n )的极小生成元系,再由嵌入维数的概念便得到了定理1。
定 理1 若m ,k ,n ∈ℕ ,2 ≤m ≤2n,k 为 奇 数 且1≤k <2m-1,则e( T( m,k,n ))=n+m 且{s0,s1,…,sn+m-1}是T( m,k,n )的极小生成元系。
证明 根据引理2和引理3即证。
2 T( m,k,n )的Apéry集
下面主要探究数字半群T( m,k,n )的Apéry集方面的一些性质。
令S 是数字半群,x ∈S{ 0 },定义S 中x 的Apéry 集[1]为Ap( S,x )={ s ∈S |s-x ∉S },而Ap( S,x )集合的势等于x,记Ap( S,x )={ ω( 0 ),ω( 1 ),…,ω( x-1 )}。这里,对∀i ∈{ 0,1,…,x-1 },ω( i )是S中与i模x同余的最小元素。

注1 用A( r )表示所有元素( a1,a2,…,ar)∈{ 0,1,2}r的集合且元素( a1,a2,…,ar)满足条件:若1≤i <j <r,aj=2, 则ai=0。
引理5 若m,k,n ∈ℕ,2 ≤m ≤2n,k为奇数且1≤k <2m-1,令T( m,k,n )是由{ s0,s1,…,sn+(m-1)}极小生成的数字半群,则
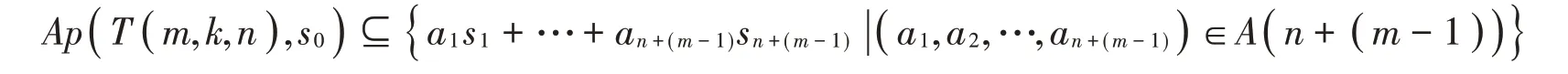
证明 证明过程[12]中引理3.1相同。
引理6[10]在常设符号下,若m,k,n ∈ℕ,2 ≤m ≤2n,k 为奇数且1≤k <2m-1,若x′∈T( m,k,n ),x′≡0 mod s0不成立,则x′-1∈T( m,k,n )。
引理7[10]在常设符号下,若m,k,n ∈ℕ,2 ≤m ≤2n,k 为奇数且1≤k <2m-1,令ω( i )是T( m,k,n )中与i模s0同余的最小元素,则∀i ∈{ 0,1,…,s0-1 },ω( 0 )<ω( 1 )<…<ω( s0-1 )。
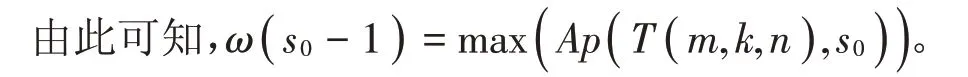
上述引理5并没有得到T( m,k,n )的一个确切Apéry集,而且当k不同时,数字半群T( m,n,k )对应的Apéry集都不相同,情况比较复杂。因此下面将针对k=2m-1-1和k=2t-1(t ∈ℕ且t ≥1)这两种特殊情况,探究使引理5等号成立的条件,确定这两种情况下的T( m,k,n )的Apéry集,进而求出Frobenius数计算公式。
3 k=2m-1 -1时,T( m,k,n )的Frobenius数
这里,令k=2m-1-1,则2m-k=2m-1+1,所以
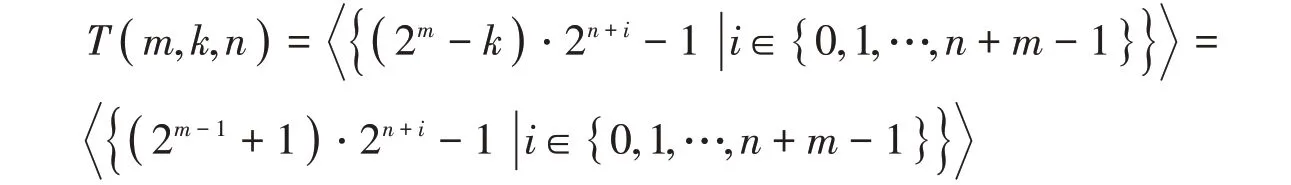
且e( T( m,k,n ))=n+m,而对于∀i ∈ℕ,这里si= ( 2m-1+1 )·2n+i-1∈T( m,k,n )。
注2 (1)设X是一个非空集合,P为条件,因此定义#X表示集合X的势;X |P是指满足条件P的X的子集。
(2)令r是正整数,( a1,a2,…,ar),( b1,b2,…,br)∈A( r ),在A( r )上定义如下关系:
( a1,a2,…,ar)≤r( b1,b2,…,br)⇔∀m′>0,am′=bm′或∃m′>0,∀i <m′,am′<bm′,ai=bi,
由此可知≤r是A( r )上的全序。
引理8 在常设符号下,若m,k,n ∈ℕ,2 ≤m ≤2n,k=2m-1-1,则max( Ap( T( m,k,n ),s0))≤sn+sn+(m-1)。
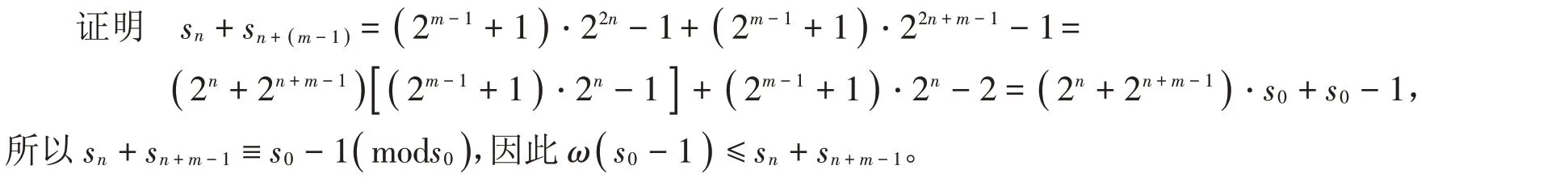
根据引理8,可以得到如下结论。
引理9 在常设符号下,若m,k,n ∈ℕ,2 ≤m ≤2n,k=2m-1-1,则
(1)2sn+m-1∉Ap( T( m,k,n ),s0);
(2)对∀i ∈{ 0,1,…,n+m-1 },sn+sn+m-1+si∉Ap( T( m,k,n ),s0)。
注3 现定义R( n+m-1 )是满足下列条件序列( a1,a2,…,an+m-1)∈A( n+m-1 )的集合:
①an+m-1∈{ 0,1 };
②若n <i <n+m-1,an=an+m-1=1,则ai=0,同时,令( a′1,a′2,…,a′n-1)∈A( n-1 ),则R( n+m-1 )= A( n+m-1 )|( a1,a2,…,an+m-1)≤n+m-1( a′1,a′2,…,a′n-1,1,0,…,0,1 )。
引理10 在常设符号下,若m,k,n ∈ℕ,2 ≤m ≤2n,k=2m-1-1,则
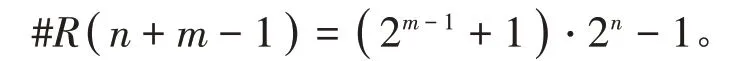
证明 下面分成2种情况进行讨论。
(1)若( a1,…,an+m-1)∈R( n+m-1 ),2 ∉{ a1,…,an+m-1},则对于∀i ∈{ 1,2,…,n-1 },ai∈{ 0,1 }。
又因为( an,an+1,…,an+m-2,an+m-1)≤m( 1,0,…,0,1 ),所以
①当( an,an+1,…,an+m-2,an+m-1)<m( 1,0,…,0,1 )时,#R( n+m-1 )=2n-1·( 2m-1+1 );
②当( an,an+1,…,an+m-2,an+m-1)= ( 1,0,…,0,1 )时,#R( n+m-1 )=1。
因此,# R( n+m-1 )|2 ∉{ a1,…,an+m-1}= ( 2m-1+1 )·2n-1+1=2n+m-2+2n-1+1。
(2)若( a1,…,an+m-1)∈R( n+m-1 ),2 ∈{ a1,…,an+m-1},则
①当2 ∈{ an,…,an+m-1}时,# R( n+m-1 )|2 ∈{ an,…,an+m-1}=2m-1-1;

所以# R( n+m-1 )|2 ∈{ a1,……,an+m-1}=2n+m-2+2n-1-2m-1-1+2m-1-1=2n+m-2+2n-1-2
因此,综合上述有#R( n+m-1 )=2n+m-1+2n-2+1 = ( 2m-1+1 )·2n-1。
根据上述引理的证明,得到了如下当k=2m-1-1时,引理5等号成立时的情况。
定理2 在常设符号下,若m,k,n ∈ℕ,2 ≤m ≤2n,k=2m-1-1,令T( m,k,n )是由{ s0,s1,…,sn+(m-1)}极小生成的数字半群,则

令S 是数字半群,x ∈S{ 0 },已知F( S )=max Ap( S,x )-x[1],因此可以得到如下关于T( m,k,n )的Frobenius数计算公式。
推论1 在常设符号下,若m,k,n ∈ℕ,2 ≤m ≤2n,k=2m-1-1,则

4 k=2t -1( t ≥1 )时,T( m,k,n )的Frobenius数
这里,k=2t-1(这里t ∈ℕ且t ≥1),则2m-k >0,故m ≥t+1,所以

引理11[12]令r是正整数,则#A( r )=2r+1-1。
引理13 在常设符号下,若m,k,n ∈ℕ,k=2t-1(t ∈ℕ且t ≥1),t+1≤m ≤2n,则
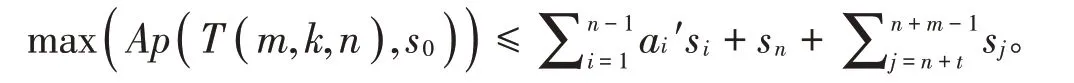
证明 对∀i ∈ℕ,有si=+2i-1,
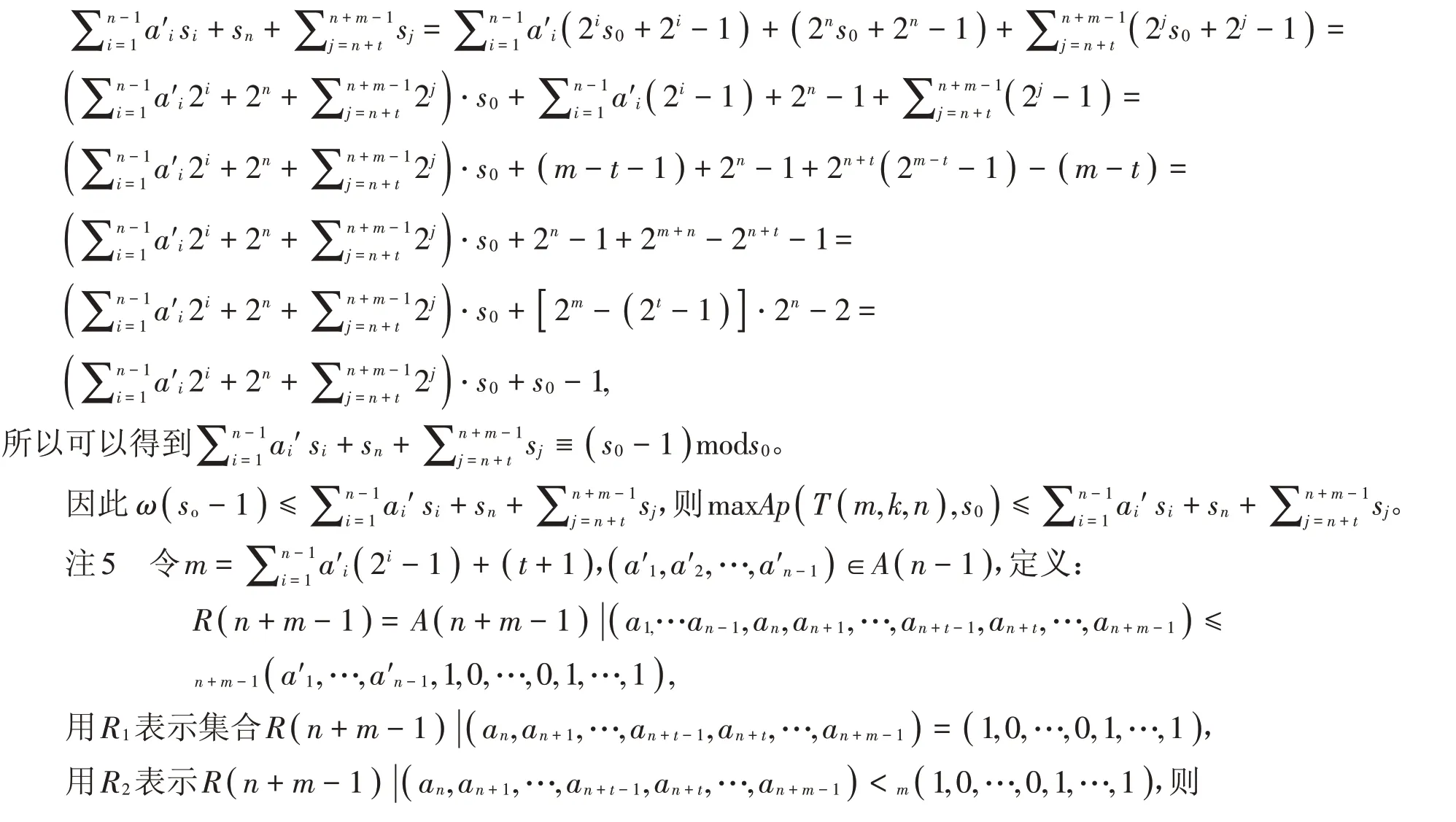
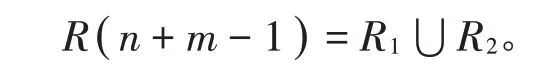
引理14 在常设符号下,若m,k,n ∈ℕ,k=2t-1(t ∈ℕ且t ≥1),t+1≤m ≤2n,则

此时分2种情况进行讨论:

因此,综合上述有
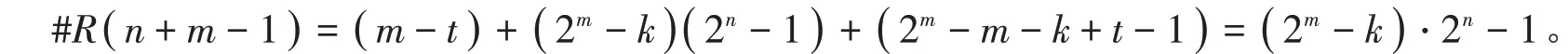
根据上述引理证明,可以得到关于k=2t-1(t ∈ℕ且t ≥1)时T(m,k,n) 的确切的Apéry集。
定理3 在常设符号下,若m,k,n ∈ℕ,k=2t-1(t ∈ℕ 且t ≥1),t+1≤m ≤2n,令T(m,k,n) 是由{s0,s1,…,sn+(m-1)}极小生成的数字半群,则
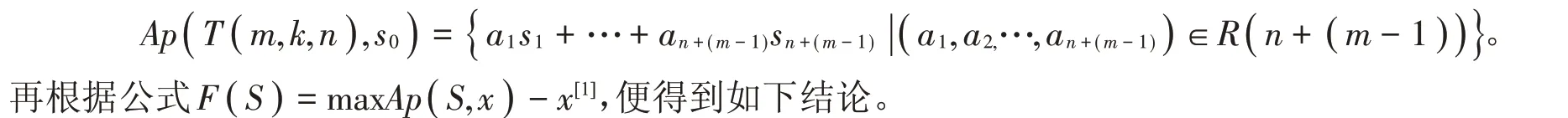
推论2 常设符号下,若m,k,n ∈ℕ,k=2t-1(t ∈ℕ且t ≥1),t+1≤m ≤2n,则
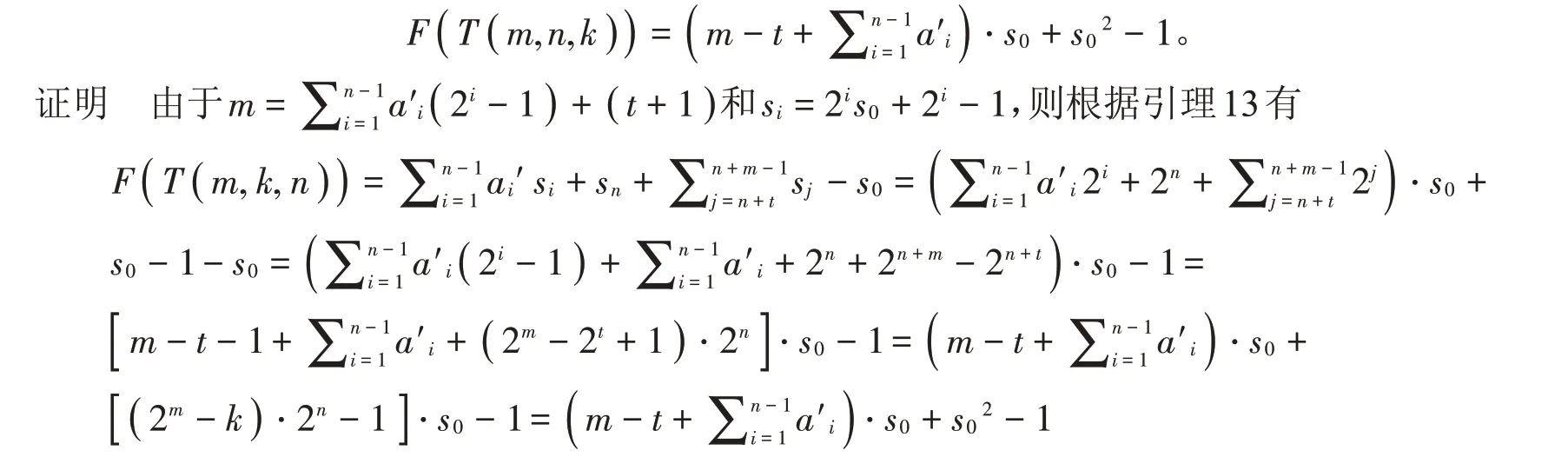
例2 令t=2,则k=3,所以令m=4时,T( 4,3,n )=13·2n+i-1 |i ∈ℕ,再令n=2,则根据定理1 可知51,103,207,415,831,1663是T( 4,3,2 )的极小生成元系,e( T( 4,3,2 ))=6。根据引理14 可得

所以根据定理3可知

5 结束语
本文在Gu等人研究的数字半群基础上,研究了新数字半群T( m,k,n )的Frobenius问题,但由于不同k的取值导致数字半群T( m,k,n )的Frobenius数的计算公式也不同,情况多而复杂,所以这里只探讨其中两类情况。而对于k的其他取值情况下,数字半群T( m,k,n )的Frobenius问题仍然有待于我们继续深入探究。

