锥形腔小孔节流空气静压支承轴承优化设计
(1.青海民族大学土木与交通工程学院, 青海 西宁810007;2.中国工程物理研究院总体工程研究所, 四川绵阳 621900)
引言
空气静压支承轴承具有精度高、摩擦小、隔振性能好的优点。相比传统的接触式轴承,空气静压轴承可大幅提高主轴转速、支承精度并降低功耗,相关设备在采用该类轴承后的加工精度可达到纳米量级。因此,空气静压轴承广泛应用于超精密加工或测量设备[1-2]。在该类轴承可采用的多种节流器中,小孔节流器由于制造简单且可维护性良好,获得了最普遍的应用。小孔节流空气静压支承轴承的设计参数包括轴承的几何尺寸、小孔节流器尺寸以及工作状态参数,这些参数决定着轴承的力学性能,从而进一步影响着超精密加工或测量装备的使用性能。因此,准确分析轴承参数与力学性能间的关系,通过参数优化获取使力学性能最优的参数组合,在工程中具有重要的意义。
对小孔节流空气静压支承轴承的力学性能已有广泛的研究,主要讨论轴承参数对力学性能的影响。在设计中,不仅需要获取优良的承载力、刚度等力学性能,为使轴承更加稳定的工作,还需提升其动力学稳定性,例如,需考虑微振动的消除。常采用优化设计的方法在给定工况下获取最优的轴承参数组合[3-4],优化建模依赖于对轴承力学性能与流场特性的分析。在轴承小孔下游可视工况需求增加气腔,目前较为常见的气腔包括圆柱形腔、锥形腔、半球形腔等[5]。气腔的增加有助于改善承载力等静力学性能[6],但由于气容增大,也增加了产生气锤激振的风险[7],因此,在设计中应根据工况合理的布置气腔。对轴承力学性能的研究主要通过解析计算、实验研究以及数值仿真的方式进行。解析计算常用于获取无腔时轴承的承载力、刚度等力学性能[8-9]。在层流假设下,基于轴承气膜的几何特性简化流体力学控制方程组,即可直接求解或进一步推导得到雷诺润滑方程后再进行求解,获取气膜压力分布,进而可计算承载力与刚度。解析分析主要用于无腔轴承的计算,而增加气腔后,三维流动效应明显,使解析分析的一维流假设失效,从而限制了方法的推广使用,而数值仿真的应用更加普遍。相比解析计算,在以CFD(Computational Fluid Dynamics)分析为基础的数值仿真中可直接建立气膜流场的三维流动数值模型,由于避免了相关假设的引入,因此计算精度更高,并且,也可考虑包含气腔或流动为湍流时的工况。通过数值仿真,可进行气膜流场分析,在轴承力学性能的研究中具有重要意义,尤其在轴承微振动产生机理的研究中,基于数值仿真进行流场分析的方式为主要的研究手段。ELESHAKY[10]和YOSHIMOTO[11]研究了气膜中超音速区与激波的形成机理。CHEN[12]对比分析了不同腔形下的气膜流场结构,指出漩涡流动是引起轴承微振动的主要原因,LI[13]讨论了气膜流场中漩涡流动与微振动的关系。LI[14]指出,在无腔轴承的设计中,应消除超音速区,因为当超音速区形成后有可能产生激波并形成大逆压梯度,从而引起流动分离并形成漩涡流动,产生微振动。LI[15]通过数值仿真,分析了带圆柱腔轴承的设计参数对力学性能的影响。采用近似模型拟合,还可获取带腔轴承力学性能与设计参数间的相关性数学模型[16]。总体而言,解析求解使用方便,尤其适用于气膜构型复杂而不利于数值仿真建模的无腔静压轴颈轴承设计,但由于各种假设的引入削弱了计算精度,且无法分析微振动;数值仿真的计算精度高,但建模复杂,且在设计前还需建立轴承参数与力学性能的相关性数学模型[14, 16]。腔形或轴承参数不同,轴承间隙流场结构差异也较大,相应的,对力学性能的影响也不相同。目前针对无腔或圆柱腔轴承的研究较为普遍,但尚缺锥形腔轴承流场分析与参数优化设计方面的研究。在设计中调整锥腔的锥度会显著改变流场结构,也增加了设计难度。因此,对该型轴承,需首先分析不同轴承参数下的流场结构,并基于流场分析,进一步考虑锥腔的形状优化以提升轴承的力学性能。
本研究以单孔圆锥腔空气静压支承轴承为研究对象,进行力学性能的分析与优化。首先进行轴承间隙流场分析,讨论气腔、气膜中超音速区、激波与漩涡流动的形成,分析微振动的产生条件;其次,通过数值仿真采样计算,基于径向基神经网络模型建立轴承参数与力学性能的相关性数学模型;最后,基于流场分析结论,在给定负载下以轴承气膜刚度最大为设计目标进行参数优化,考虑微振动的消除,建立优化数学模型。通过优化设计进一步讨论了轴承参数对力学性能的影响。
1 轴承构型与流场分析参数
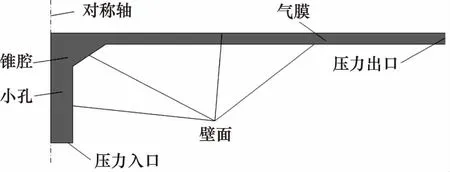
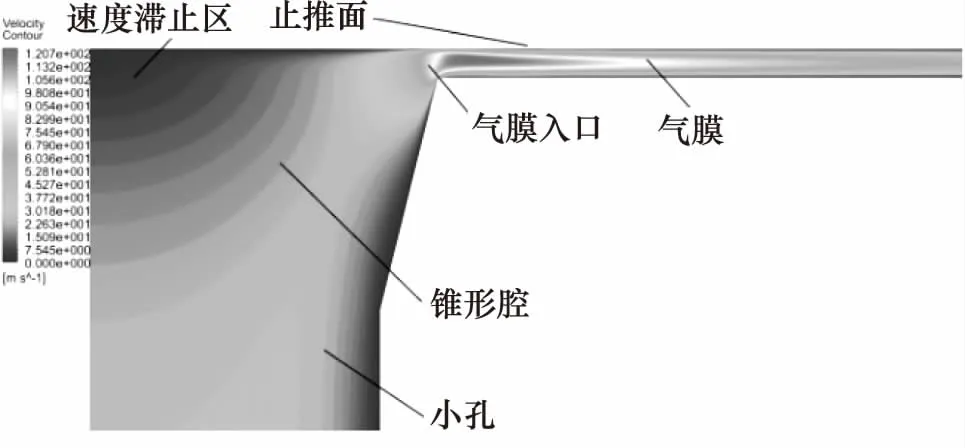
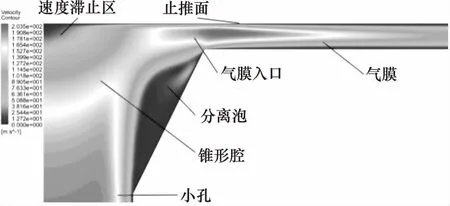
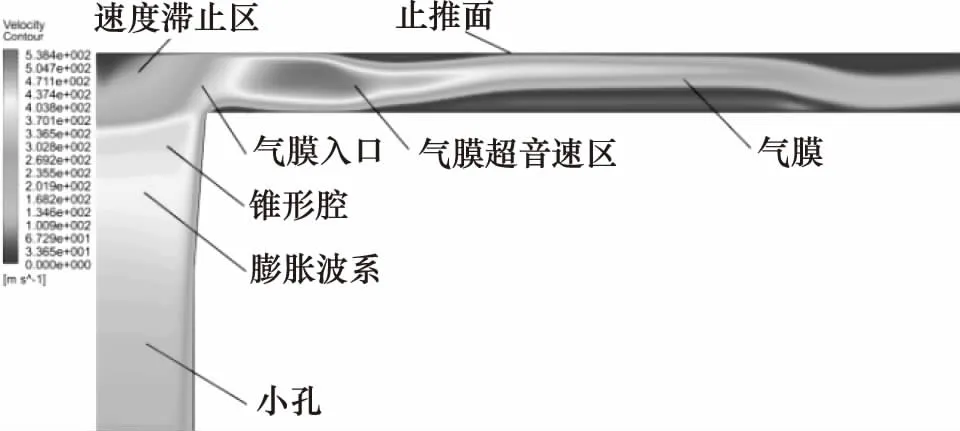
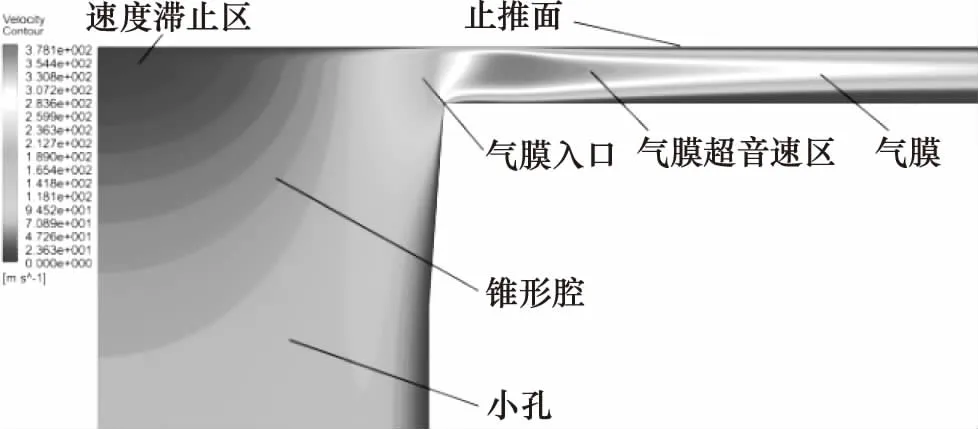
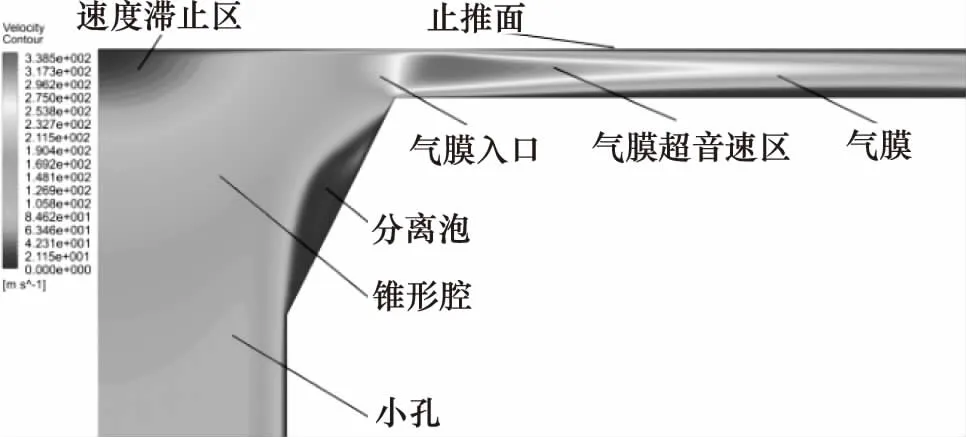
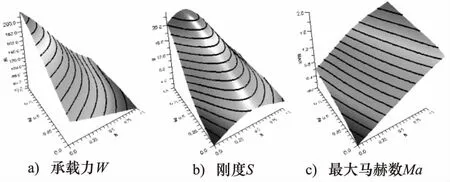
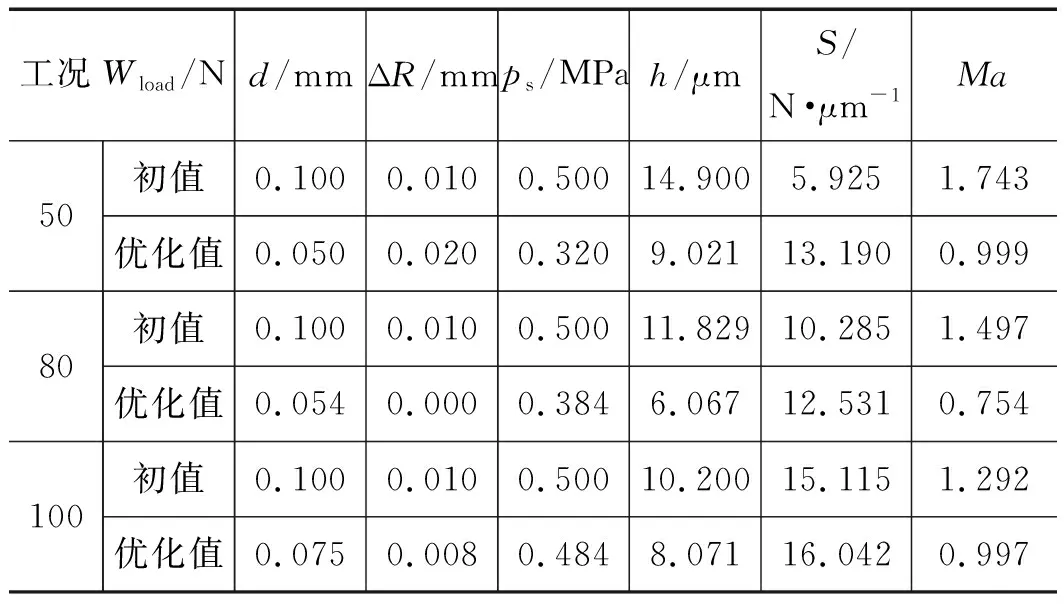
锥形腔单孔节流空气静压支承止推轴承如图1所示,由外部供气源供气,气流经供气通道,并经过小孔节流器进入锥形腔,其后进入轴承间隙形成气膜,最终气流由轴承外边界流出。轴承参数主要包括轴承的几何尺寸、节流尺寸以及工作状态参数。各参数的值或设计范围为:小孔长l为0.16 mm、腔深V为0.04 mm、轴承直径Фt为50 mm、气膜厚(5 μm 图1 锥形腔单孔节流空气静压支承止推轴承结构 轴承参数直接决定了轴承间隙的流场特性,从而影响着力学性能。因此,在力学性能研究中,应首先讨论轴承参数对流场特性的影响。由于气膜厚度仅为微米量级,故目前尚无有效手段直接通过实验实测观察详细的流场结构,有关气膜流场特性的研究主要通过数值仿真进行。图1所示轴承的气膜流场中,由于气膜几何具有旋转轴对称特性,因此以旋转轴对称二维模型建立流场分析数值模型,如图2所示。 图2 气膜流场与边界条件 小孔入口设置为压力入口,压力等于供气压。在气膜出口设置为压力出口,压力为大气压。在对称轴处设置旋转轴对称边界。轴承壁、小孔壁设置为壁面,满足无滑移条件,为绝热不可穿透壁面。流动介质为空气,为理想可压缩气体,动力黏度以Sutherland公式[12]计算。为判断流动状态,首先进行试算,在不同几何参数的上下限组合下,保持供气压ps为最大值0.7 MPa,计算气膜流场中的最大雷诺数Re,结果如表1。 表1 雷诺数计算结果 由表1可见,各组雷诺数均小于3000,因此在后续数值仿真中采用层流模型[10]。 轴承间隙,即小孔、气腔与气膜的流场特性直接影响着轴承的力学性能,因此在设计中需重点讨论。在特定的轴承参数组合下,气膜中有可能形成漩涡流动并进一步引起气膜压力波动,从而使轴承产生微振动[12-14]。由于微振动的产生会削弱轴承的动力学稳定性,因此在设计中需要通过参数设计尽量避免漩涡流动的形成,即消除微振动。对于无腔小孔节流空气静压支承轴承,在气膜中有可能出现超音速区,若同时存在激波则会在气膜中形成较大的逆压梯度,进而,流动分离的产生可形成漩涡流动并引起微振动。因此,在设计中需避免超音速区的产生[14]。在圆柱腔轴承的气膜流场中,由于气腔容积远大于小孔,因此在腔中会产生内部射流流场,由于止推面的阻挡会形成漩涡流动,在设计中可通过降低入口雷诺数来削弱漩涡流动的影响[17]。对于采用锥腔的小孔节流空气静压支承轴承,尚未有研究讨论其在不同轴承参数组合下的详细气膜流场结构,从而,在设计中也不能有效利用流场分析的结论削弱或消除轴承微振动。 为验证数值分析的准确性,采用与YOSHIMOTO[11]在研究中所使用相同的轴承参数进行数值仿真,获取压力沿轴承止推面径向的分布,并将数值分析结果与YOSHIMOTO的实测结果进行对比,如图3所示。其中R为轴承半径。可见仿真结果与实测结果吻合良好,数值仿真具有足够的精度。 在轴承间隙流场分析中讨论的重点为小孔出口及气膜入口位置的流动特性。在给定轴承参数的设计范围内,锥腔轴承的流场按有、无锥腔中的流动分离区及有、无超音速区,主要呈现出4种不同的流动结构。其中,流场结构1的速度云图如图4所示。气流通过小孔进入气腔,由于止推面的阻挡,在止推面与对称轴相交处形成速度滞止区,该区域压力较高, 在其挤压下,气流在锥腔内发生偏转,进入气膜。在气膜入口,由于有效流道截面积最小,形成了流场中的最大速度区域。由于最大马赫数Ma为0.36,故无超音速区,且由于锥度较小,在锥腔中未形成明显的流动分离区。流场结构1即为无分离泡、无超音速区的情况。 图3 单孔空气静压止推轴承径向压力分布仿真与实测对比 图4 轴承间隙流场结构1(Ma=0.36) 流场结构2如图5所示,与流场结构1类似,其中仍然无超音速区。然而,由于锥角加大,在锥腔中出现了明显的分离泡,分离泡与速度滞止区减小了气流在锥腔中的有效流道截面积,当气流流入气膜后,随着流道膨胀,有效流道截面积再次增加。流场结构2即为有分离泡、无超音速区的情况。 图5 轴承间隙流场结构2(Ma=0.62) 在流场结构3中,无分离泡存在,但存在超音速区,速度云图如图6、图7所示。当气流在小孔中流动时,边界层不断增厚,使有效流道截面积减小,当气流流经小孔进入锥腔时,由于在锥腔入口存在壁面的偏转,气流的有效流道截面积增加,而速度滞止区的存在会导致有效流道截面积的再次减小,直至气流流入气膜。气流过气膜入口进一步流动时,由于流道膨胀,使有效流道截面积再增加,在气膜入口位置,截面积为最小值。由此可见,有效流道截面积经历了2次先减小、再增加的过程,第1次发生于气腔入口,第2次发生于气膜入口。因此,类似于拉瓦尔喷管,存在产生超音速流的条件,即有效流道截面积为先减小、后增加时,若在最小流道截面积处达到音速,则流场中产生超音速区。在图6中,于小孔出口位置形成了超音速流动,在锥腔中可观察到明显的膨胀波系,气流流过膨胀波系,速度进一步增加,在进入气膜后气流速度达到最大值。在图7中,在小孔出口位置流动未达到音速,故在气腔中无超音速区,而在气膜入口处,由于流速达到音速,故形成了超音速区。在流场结构3所讨论的2种情况中,无论在气腔中有无超音速区,在气膜中均有超音速区产生。 图6 轴承间隙流场结构3:情况一(Ma=2.22) 图7 轴承间隙流场结构3:情况二(Ma=1.28) 在流场结构4中,存在分离泡,也存在超音速区,如图8所示。与流场结构3类似,在速度滞止区及分离泡的影响下,有效流道截面积也存在两次先减小、再增加的过程,一次发生于气腔入口,一次发生于气膜入口。在最小有效流道截面积处的流速若达到音速,便会形成超音速区。 由分析可见,流场结构1、2中未存在超音速流,而在流场结构3、4中,存在超音速流。并且,在流场结构1、3中,不存在分离泡,在流场结构2、4中,有分离泡。分离泡出现的主要原因是小孔出口处壁面的折转,即此处的流动分离为强迫分离,分离点即为壁面折转点。并且,由图5及图8可见,分离泡仅存在于锥腔之中,紧贴锥腔壁面,为局部分离[18],故虽然在分离区有涡量存在,但其并不随着流动的发展而演变为漩涡流动,并进一步进入气膜,因此,锥腔中存在的分离泡不会引起气膜之中的压力波动。在流场结构3、4中存在超音速区,其可只存在于气膜中,如图7、图8,也可同时存在于气腔与气膜中,如图6,在两种情况下,气膜中均有超音速流存在,文献[14]表明,当气膜入口存在超音速流动时,由于边界层的影响,在超音速区末端即有可能产生激波,若激波形成,则会引起大逆压梯度并引起边界层分离,从而产生漩涡流动。由于漩涡中心为低压区,故在漩涡不断的产生与流动过程中,会引起气膜流场的压力波动。由于气膜直接与止推面接触,因此只有发生于气膜中的压力波动,才可引起微振动,即气膜中的压力波动引起轴承承载力的波动从而引起微振动。故而,为避免微振动的产生,需要通过参数设计消除气膜中的超音速流,在具体设计中可控制流场最大马赫数小于1加以实现。 图8 轴承间隙流场结构4(Ma=1.11) 相比无腔轴承,锥腔的存在可增加承载力[6]。而对于圆柱腔轴承,在相同的腔半径、腔深下,圆柱腔比锥腔的气容更大,故承载力更大,但也更易于引起气锤振动[7]。采用圆柱腔时,腔半径常远大于小孔孔径,气流自小孔进入气腔时产生内部射流流场,由于止推面的阻挡,在腔内即形成漩涡,漩涡强度随雷诺数增加而增加[17,19];并且,相比锥腔,圆柱腔更大的气腔容积为漩涡流动提供了更大的发展空间,意味着漩涡流的影响更大。故此,在由漩涡流动引起微振动所代表的动力学稳定性方面,锥腔的性能更佳。 传统的力学性能解析计算公式主要应用于无腔轴承,当增加气腔后三维流动效应显著,使采用了一维流假设的解析公式无法推广使用。并且,在推导中引入的一系列假设也削弱了解析计算精度。因此,本研究通过数值仿真在参数设计范围内进行样本采样,并建立近似模型以研究轴承的力学性能。考虑的力学性能包括承载力W、刚度S及流场最大马赫数Ma。在设计范围内布置样本点,考虑4因素7水平,建立正交表L49(74),共进行49组数值仿真采样。其中因素为气膜厚h、小孔孔径d、锥腔底面与顶面半径差ΔR、供气压ps。采用径向基神经网络(RBF)模型[16]建立近似模型,获取力学性能与轴承参数间的关系。基于RBF模型的拟合函数如式(1): (1) 其中,φj(x)为径向基函数,形式为: φj(x)=||x-xj||c (2) 其中,G(x)表示承载力、刚度或最大马赫数。α1,α2,…,αN+1为未知系数,系数c通过最小化残差得到。在拟合前,需对各变量进行归一化处理。 将各样本点xi与对应的样本值yi代入式(1)中,求解方程组式(3): (3) 得到α1,α2,…,αN+1,便获取了式(1)函数。基于拟合函数,可获取承载力、刚度以及最大马赫数与轴承参数间的关系,如图9所示。 图9 承载力、刚度、最大马赫数随气膜厚、供气压的变化(d=0.1 mm, ΔR=0.01 mm) 优化设计的目的为在一定约束下寻求特定的参数组合,使轴承的力学性能最优。在本研究中,优化目标为在给定的轴承负载Wload下,寻求使刚度最大的设计参数组合。并且,为保证消除轴承的微振动,流场最大马赫数需小于1。优化设计的数学模型如式(4),设计变量包括d、ΔR以及ps。 maxS; s.t.W=Wload Ma<1; (d,ΔR,ps)T∈E (4) 其中,E为可行设计域。分别考虑给定负载Wload为50, 80, 100 N。优化流程如图10所示,其中,目标与约束函数,即S(d,ΔR,ps)、Ma(d,ΔR,ps)与W(d,ΔR,ps)均采用前述基于RBF模型建立的拟合函数。Ma(d,ΔR,ps)小于1即消除微振动;W(d,ΔR,ps)等于Wload即满足给定负载要求。 图10 优化设计流程 优化结果如表2,优化设计采用多学科优化软件Isight进行。其中,寻优算法采用多岛遗传算法与Hooke-Jeeves直接搜索算法,前者用于全局寻优,后者在前者优化值的基础上进一步搜索更精确的最优点。 表2 优化结果 由表2可见,在相同的初始参数下,随着给定轴承载荷的增加,气膜厚度相应减小,最大马赫数也减小,这是由于气膜厚度减小导致流道气阻增加,进而引起气体流量减小所致。优化后,刚度相比初始值均有增加,在给定负载为50 N时,刚度增加122.6%;负载为80 N时,刚度增加21.8%;负载为100 N时,刚度增加6.1%。负载为100 N时刚度增加较少,但满足了最大马赫数小于1的约束。在优化结果中,各组最大马赫数均小于1,即无微振动。其中,负载为50 N与100 N时的约束接近临界值,为80 N时未达到临界值。在3组优化中,小孔孔径的优化结果均较小,意味着在小孔径下,轴承的力学性能更优,但具体最优值应由优化设计确定。 以锥形腔小孔节流空气静压支承止推轴承为研究对象,首先分析轴承间隙流场特性,讨论超音速区与漩涡流动的形成过程;其次,考虑气膜厚度、小孔孔径、锥腔底面与顶面半径差、供气压,基于径向基神经网络模型建立了轴承承载力、刚度、最大马赫数和设计参数的相关性数学模型;最后,在给定轴承负载下对轴承参数进行了优化设计,限制流场最大马赫数小于1以消除超音速区、漩涡流动与微振动,寻得了使轴承力学性能最优的参数组合。 通过分析可以得到以下结论:在锥形腔小孔节流空气静压支承止推轴承的间隙流场中,按有、无超音速区及有、无锥腔内的分离泡,可将流场分为4类。在流场中存在着分离泡、边界层与马赫波的相互作用,流场结构复杂。为消除微振动对轴承稳定性的不利影响,在设计中应避免超音速区的产生,因为消除超音速区可有效避免激波以及气膜内漩涡流动的产生,即消除了微振动。 在参数设计范围内,当轴承载荷给定时可通过优化设计获取使轴承力学性能最优的参数组合,采用全局优化算法与传统的直接搜索算法相结合的方式,可获取高效的优化结果,刚度最大提升122.6%。在不同工况下的优化结果表明,采用小孔径有利于提升轴承的力学性能,但具体的孔径值仍需以优化设计确定,由于在制造中小孔孔径的减小会增加制造成本,因此,在设计中还应权衡轴承的设计性能与制造成本,选择合适的孔径。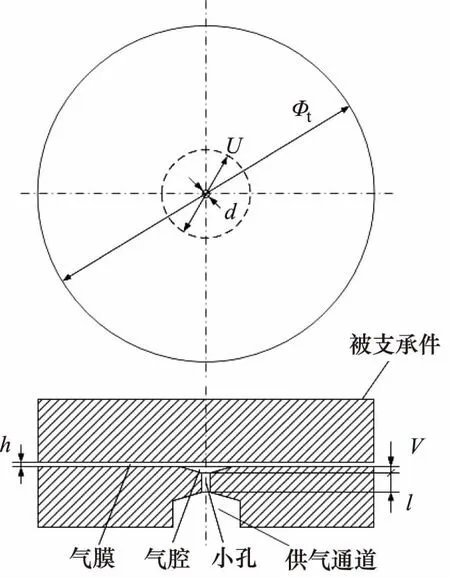

2 轴承间隙流场特性分析

3 轴承力学性能的数值建模
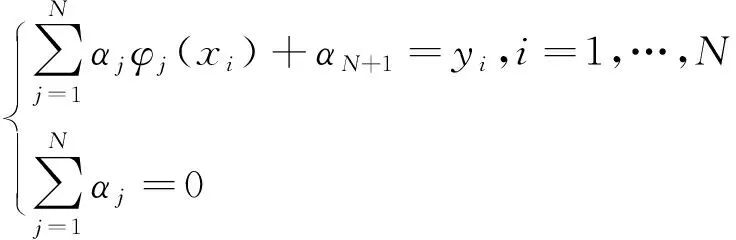
4 轴承优化设计

5 结论

