音圈电机直驱高速开关阀动态特性研究

刘晓鹏1,2， 聂松林1,2， 纪 辉1,2， 尹方龙1,2， 潘 燚， 孙有伟

(1.北京工业大学机电学院， 北京 100124； 2.北京工业大学先进制造技术北京市重点实验室， 北京 100124；3.中船重工七O五研究所昆明分部， 云南昆明 650032)

引言

电液数字控制技术作为实现机电一体化的重要手段，是实现对液压系统进行高速、高精度控制的理想方法，已广泛应用于航空航天、汽车、冶金、农业机械、工程机械等重要领域[1]。高速开关阀是实现电液数字控制技术的关键元件之一[2]，它的控制并非简单开关信号的控制，而是利用计算机控制其开关量来达到控制的目的[3]。传统的开关阀响应时间长、换向频率低不能很好地满足高精度的电液控制系统需求[4]。而高速开关阀具有快速开合、功率质量比大、重复精度高、抗污染且价格低廉[5-7]，能够将计算机控制技术与液压系统有机结合，实现快速、高精度的连续控制。因此，近年来对高速开关阀的研究已成为液压领域的研究热点之一。

发达国家很早就着手对高速开关阀进行了研究，最早的高速电磁开关阀可以追溯到英国的 Helenoid阀[8]和Colenoid阀[9]。此后，日本开发一种适用于油压环境、小流量的HS-G01-AR型高速开关阀[10]。Haink C.Tu[11]设计了一种广泛应用于高速换向、高速激振液压系统中的转阀式新型高速开关阀。虽然较发达国家而言，我国对高速开关阀研究开始较晚[12]，但也设计出一些新型高速开关阀。江海滨、阮健等[13]利用阀芯的2个自由度研制了一种2D高速开关阀。哈尔滨工业大学[4，14]研发了一种喷嘴挡板式高速开关阀，并针对电磁铁吸合式电磁阀在频响和输出功率方面存在的局限性，提出采用稀土超磁致伸缩材料做高速开关阀驱动器。浙江大学[15]针对气动喷射系统开发了一种新型高速开关电磁阀。

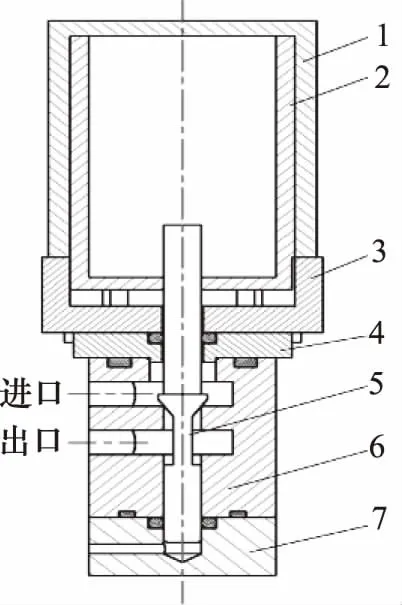
1.音圈电机定子 2.音圈电机动子 3.上端盖 4.密封板 5.阀芯 6.阀体 7.下端盖图1 音圈电机直驱高速开关阀结构原理图

现阶段，国内外针对电磁高速开关阀的研究主要是适用于油压环境，对于水压环境中的高速开关阀研究较少。为满足水下作业设备的小型化和环境相容性的要求，本研究提出了一种音圈电机直接驱动的高速开关阀。

1 音圈电机直驱高速开关阀工作原理

图1为音圈电机直驱高速开关阀结构原理图。由图可知该阀由音圈电机与锥阀阀体两部分组成。其中，音圈电机部分选用圆柱形音圈电机；锥阀阀体部分则包括铝青铜主阀体、17-4PH阀芯、上下端盖、密封板等。音圈电机与阀芯通过螺纹进行连接，端面密封采用O形圈，轴向密封采用斯特封。

在开关阀中，音圈电机正向通电，动子线圈带动锥阀阀芯向下运动，阀口关闭，如图2a所示；音圈电机反向通电，动子线圈带动锥阀阀芯向上运动，阀口开启，如图2b所示。在开关阀处于关闭或开启状态时，由于A1面积(出口处阀芯的环形面积)与A2(阀芯锥面)轴向投影面积相等，故高压水作用在A1面与A2面上的力基本一致。因此，音圈电机提供的推力满足大于阀芯与密封圈之间的摩擦力这一条件就能实现开关阀的启闭。随着所需推力的减小，有效降低了高速开关阀的体积与质量，提升了其工作性能与实际应用效果。

图2 音圈电机直驱高速开关阀工作原理图

2 音圈电机直驱高速开关阀模型

2.1 高速开关阀数学模型

1) 开关阀阀芯运动力平衡方程

根据图1所示，音圈电机正向通电，动子线圈带动锥阀阀芯向下运动，此时开关阀阀芯受到音圈电机通电后形成的拉力、水流经阀口时形成的水压稳态动力和水压瞬态动力、水流环境中的的静压力以及阀芯由于被推动后做加速运动而形成的质量惯性力和水流对其形成的黏性阻尼力的共同作用。因此音圈电机直驱高速开关阀阀芯的运动力平衡方程[16]可以表示为：

(1)

式中,F—— 音圈电机拉力，N

Fs—— 流经阀口的水压稳态动力，N

Ft—— 流经阀口的水压瞬态动力，N

Fp—— 流体的静压力，N

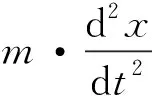
其中，流经阀口的水压稳态动力[17]可以表示为：

(2)

式中,Fs—— 流经阀口的水压稳态动力，N

dp—— 阀芯上端直径，mm

ps—— 开关阀进口压力，MPa

dm—— 阀芯上端与阀孔直径中间值，mm

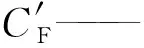
其中：

(3)

(4)

式中,da—— 阀孔直径，mm

CQ—— 流体流量系数

x—— 阀芯位移开度，mm

θ—— 阀芯锥面半锥角，(°)

2) 开关阀阀口流量连续性方程

在建立高速开关阀的数学模型时，忽略了系统相关管路和其他零部件对开关阀动态性能的影响，只考虑开关阀自身的结构参数，同时根据系统试验的实际情况，设定高速开关阀的出口直接连接水箱，即设定压力为0。则音圈电机直驱高速开关阀阀口流量连续性方程可以表示为：

(5)

式中,Q—— 阀口流量，L/min

CQ—— 锥阀阀口流量系数

x—— 阀芯位移开度，mm

da—— 阀座孔直径，mm

a—— 阀芯锥面半锥角，(°)

Δp—— 阀进出口压差，MPa

2.2 高速开关阀AMESim动态仿真模型

音圈电机直驱高速开关阀本体关键结构的参数变化能令其动态性能产生很大波动。为了提高开关阀的响应速度，需要先对其本体主要结构参数进行优化分析并通过AMESim软件建立了其AMESim动态仿真模型，如图3所示。

图3 音圈电机直驱高速开关阀AMESim动态仿真模型图

通过改变音圈电机直驱高速开关阀AMESim动态仿真模型关键结构参数(如阀芯直径d1、阀孔直径da、阀芯杆直径d2以及阀芯锥面半锥角θ等)，分析高速开关阀的关键结构参数变化对其动态性能产生的影响[18]，为进一步优化结构，提高响应速度提供理论依据。表1给出了音圈电机直驱高速开关阀关键结构参数动态仿真初始数值。

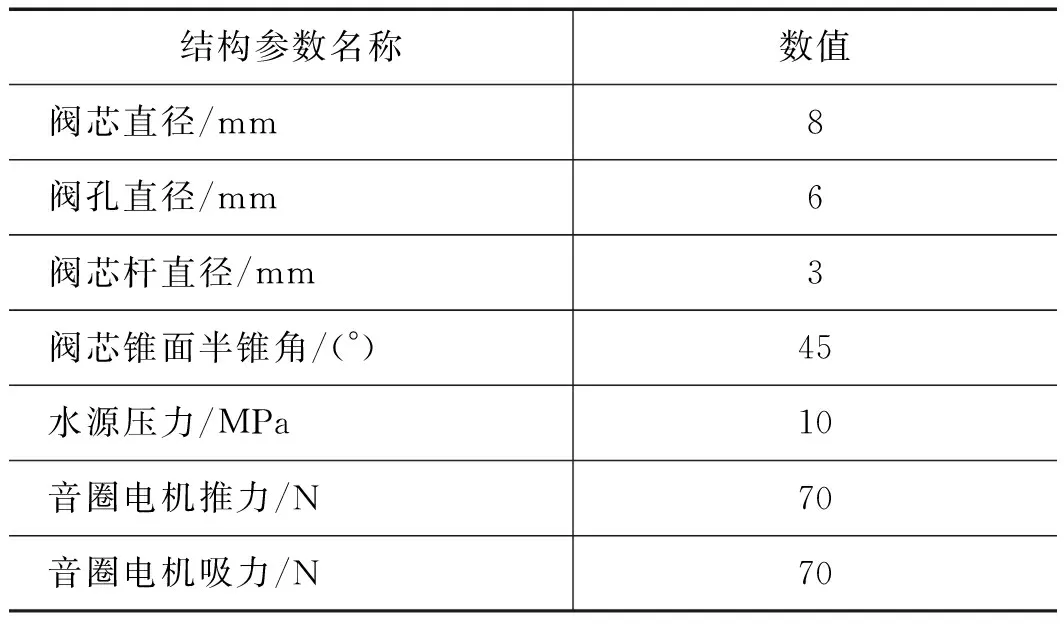
表1 开关阀AMESim模型关键结构动态仿真初始数值

3 仿真结果及分析

音圈电机直驱高速开关阀作为一种非线性耦合系统，由音圈电机和开关阀本体2部分组成。音圈电机作为整个系统的动力元件，为高速开关阀提供恒定的驱动力，此时开关阀阀芯的驱动功率与其运动速度成正比。又因为开关阀阀芯的位移量为定值，所以其运动速度与响应时间成反比。综上所述，开关阀在阀芯开启过程中驱动功率与阀芯运动速度成正比，与开关阀的响应时间成反比，即开关阀的响应时间越短，音圈电机对其驱动功率越大。音圈电机可根据工况条件选用已有的商业化产品，直接采用相关参数，减少仿真计算量。因此，高速开关阀的仿真与分析主要围绕其本体关键结构的变化进行。

3.1 基于AMESim批处理的单参数影响分析

设置其他结构参数为定值，根据音圈电机直驱式高速开关阀的实际工况，确定目标参数的极值，并在极值范围内进行基于AMESim批处理的单参数影响分析。通过对比分析高速开关阀在不同结构参数下性能指标的变化，研究单参数变化对音圈电机直驱式高速开关阀动态性能的影响。

1) 变阀芯直径时高速开关阀性能指标变化

为满足系统对高速开关阀的流量要求，将锥面阀芯直径起始值设定为7～10 mm。在其他参数不变的情况下得到的开关阀出口流量Q与时间t关系和位移x与时间t关系分别如图4、图5所示。

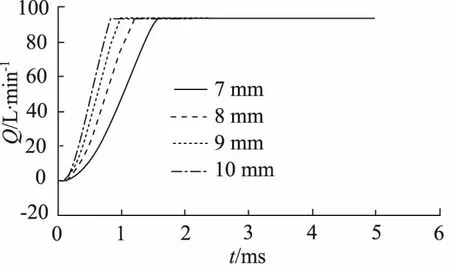
图4 不同阀芯直径下高速开关阀出口流量与时间关系

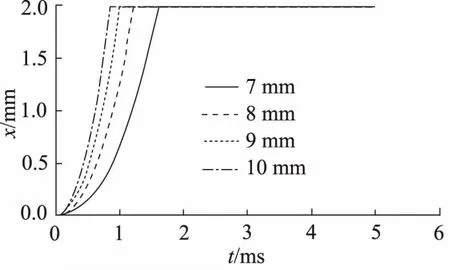
图5 不同阀芯直径下高速开关阀位移与时间关系

由图4得到，随着锥面阀芯直径的增大，高速开关阀出口流量并未发生显著变化。这是由于锥面阀芯直径增大的过程中，开关阀通流面积没有改变，所以其出口流量不会发生变化。由图5得到，随着锥面阀芯直径的增大，高速开关阀的响应时间逐步缩短。但综合考虑系统的体积和质量要求，选取开关阀锥面阀芯直径为8 mm。

2) 变阀孔直径时高速开关阀性能指标变化

为满足系统对高速开关阀的流量要求，将阀芯阀孔直径起始值设定为4～7 mm。在其他参数不变的情况下得到的开关阀出口流量Q与时间t关系和位移x与时间t关系分别如图6、图7所示。

图6 不同阀孔直径下开关阀出口流量与时间关系

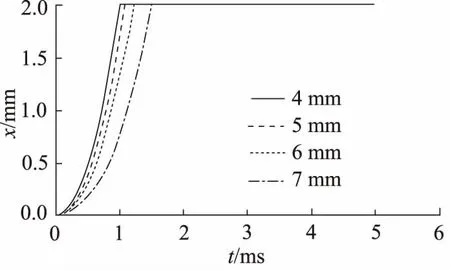
图7 不同阀孔直径下开关阀位移与时间关系

由图6得到，随着阀孔直径的增加，开关阀的通流面积增加，其出口流量会随之增加。但此时阀芯密封面积减小，开关阀密封性降低，泄漏的可能性增大。由图7得到，阀孔直径的增加将造成开关阀响应时间变长。同时，阀孔直径与阀芯直径的增加会使整个系统体积和质量变大。因此，选取锥面阀孔直径为6 mm。

3) 变阀芯杆直径时高速开关阀性能指标变化

为满足系统对高速开关阀的流量要求，将阀芯杆直径起始值设定为2～5 mm。在其他参数不变的情况下得到的开关阀出口流量Q与时间t关系和位移x与时间t关系分别如图8、图9所示。

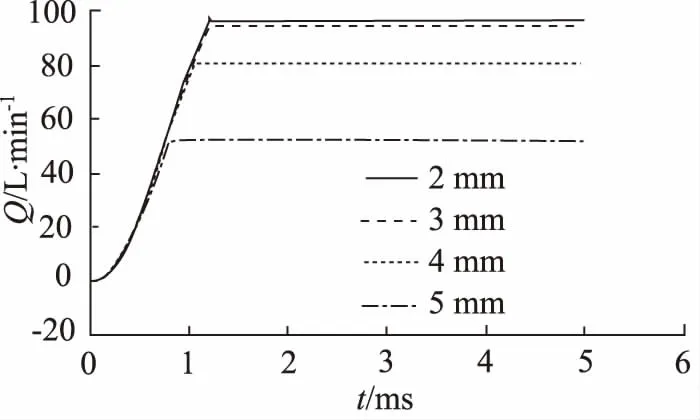
图8 不同阀芯杆直径下开关阀出口流量与时间关系

由图8得到，随着阀芯杆直径的增大，开关阀通流面积减小，其出口流量会随之降低。由图9得到，随着阀芯杆直径的增大，开关阀的响应时间逐步缩短。但综合考虑实际工况对开关阀的体积和质量要求，选取阀芯杆直径为3 mm。

图9 不同阀芯杆直径下开关阀位移与时间关系

4) 变阀芯半锥角时高速开关阀性能指标变化

参考机械设计手册中的相关要求，将阀芯锥面半锥角起始值设定为20°,30°,45°,60°,70°。在其他参数不变的情况下得到的开关阀出口流量Q与时间t关系和位移x与时间t关系分别如图10、图11所示。

图10 不同阀芯半锥角下开关阀出口流量与时间关系

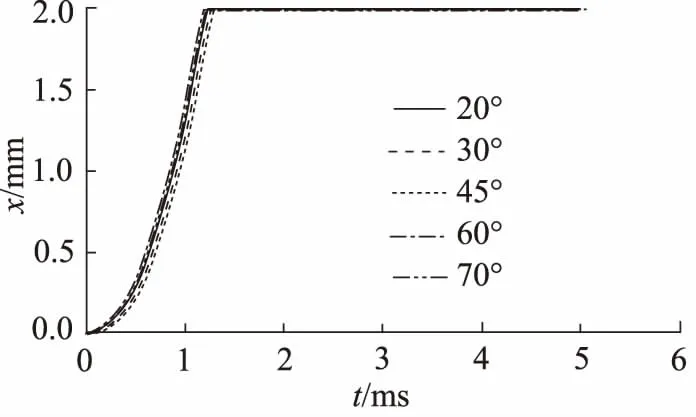
图11 不同阀芯半锥角下开关阀位移与时间关系

由图10得到，阀芯锥面半锥角以45°为分界点，当其取20°～45°时，随着角度增大，开关阀出口流量会随之增大；当其取45°～70°时，随着角度增大，开关阀出口流量基本保持不变。由图11得到，阀芯锥面半锥角的增加会提高阀芯响应速度，但影响较小。此外，考虑到开关阀的小型化，加工简单化等要求。因此，初步选取阀芯半锥角为45°。

通过基于AMESim批处理的单参数影响分析得到优化后的音圈电机直驱高速开关阀关键结构参数取值如表2所示。

表2 单参数优化后开关阀关键结构参数取值

此时开关阀响应时间最短，仅需1.186 ms，单参数具体优化结果如图12所示。

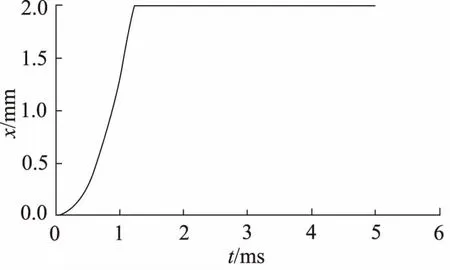
图12 单参数优化结果

3.2 基于遗传算法的多参数影响关系分析

遗传算法 (Genetic algorithm,GA)是对自然界生物进化与遗传过程的效仿[19-20]，根据生存竞争和优胜劣汰的法则，借助适应度函数进行优化计算[21]，能有效地跳出局部极值点而逐渐趋近全局最优点的一种优化方法[22]。因此，本研究采用遗传算法更有助于求解音圈电机直驱式高速开关阀的多参数优化问题。图13是使用遗传算法分析多参数影响关系流程图。

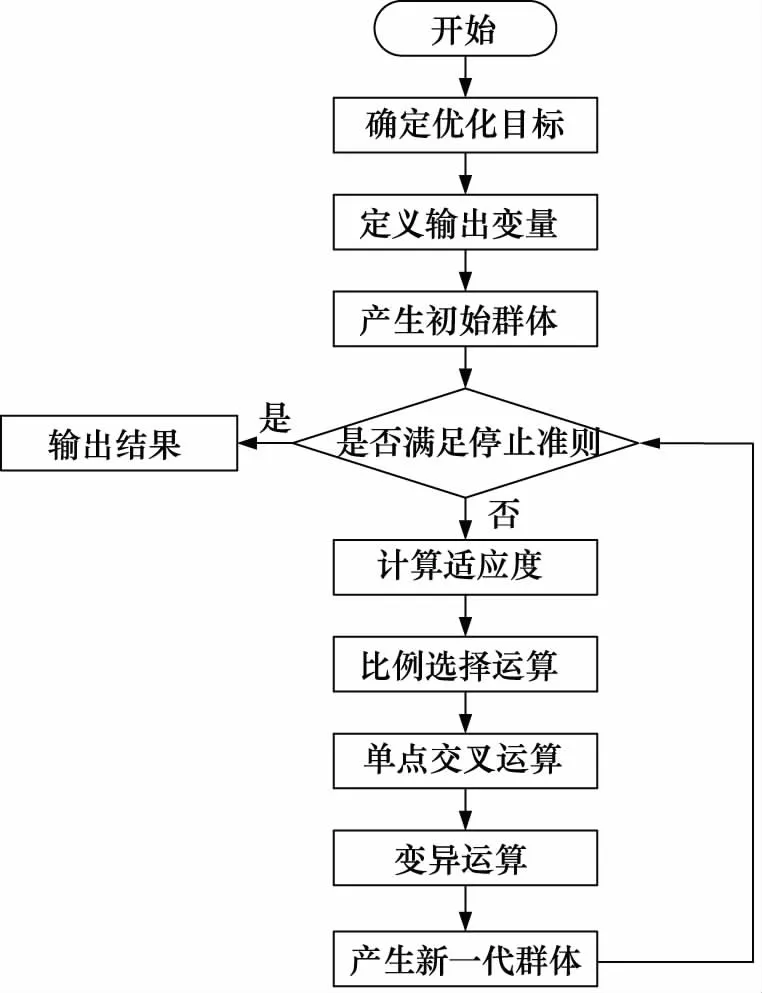
图13 遗传算法流程图

1) 确定参数范围

由于影响开关阀响应特性的因素很多，使用基于AMESim批处理分析结果来设定遗传算法的变量及参数范围能够有效减少计算量，节省优化时间。优化变量及参数范围如表3所示。

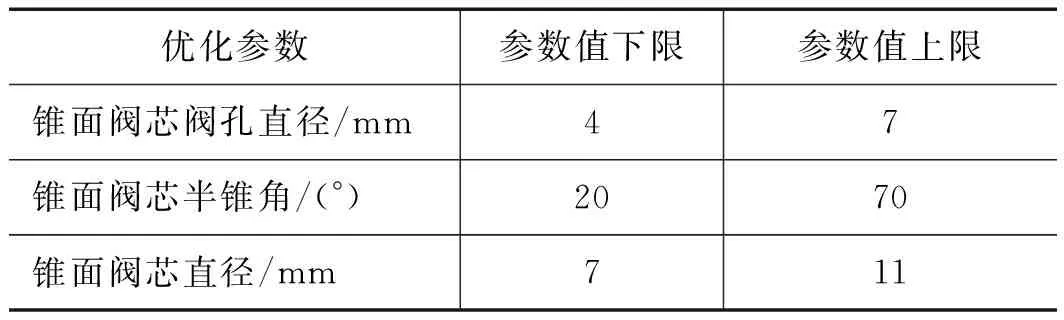
表3 优化变量及参数范围

2) 基于遗传算法的优化分析

(1) 确定优化目标。为满足音圈电机直驱式高速开关阀系统实际工作需求，设定改善其动态性能，缩短响应时间的优化目标;

(2) 定义输入输出变量。输入变量设置为AMESim批处理分析结论中对开关阀动态性能有较大影响的3个高速开关阀关键结构参数；输出变量设置为开关阀阀芯运动到额定位移时消耗的时间。

表4 Genetic algorithms各项参数取值

(3) 确定目标函数。由于最终的优化目标为响应时间，因此选择的目标函数为：

minf(x)

(6)

其中：

x∈Rngj≥0j=1,…,m

x1≤x≤x2

式中,f(x) —— 目标函数

x—— 待优化变量

gj—— 进化代数

x1—— 待优化变量下限

x2—— 待优化变量上限

(4) 优化参数，寻找最优解。本研究采用Genetic algorithms的优化方法，对各项参数的设定如表4所示。

图14 锥面阀芯直径随迭代次数的变化

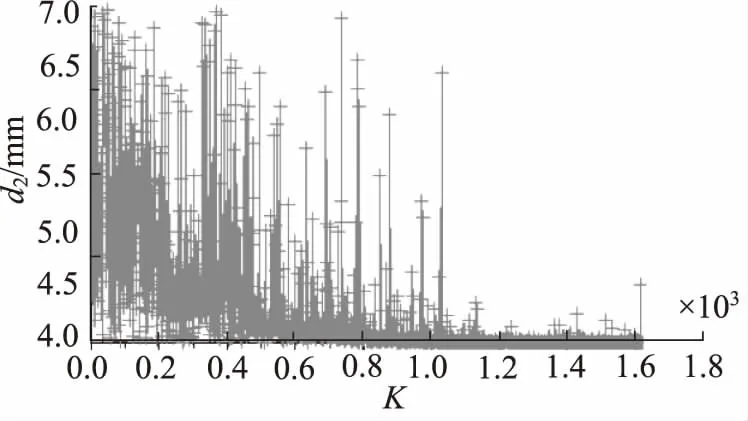
图15 锥面阀孔直径与迭代次数的变化关系

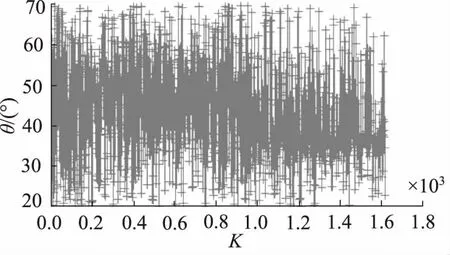
图16 阀芯锥面半锥角与迭代次数的变化关系

图17 开关阀动态响应时间与迭代次数的变化关系

将3个开关阀关键结构参数作为主要影响因子的迭代过程(即各关键结构参数与迭代次数K的关系)及动态响应迭代过程(即响应时间t与迭代次数K的关系)如图14～图17所示。从图中可以看出，基于遗传算法多参数影响关系得到的音圈电机直驱式高速开关阀主要结构参数的变化趋势与单参数优化结果基本一致，验证了仿真的正确性。

通过基于遗传算法分析得到优化后的音圈电机直驱高速开关阀关键结构参数取值如表5所示。

表5 多参数优化后开关阀关键结构参数取值

此时开关阀响应时间最短，仅需0.695 ms，多参数具体优化结果如图18所示。

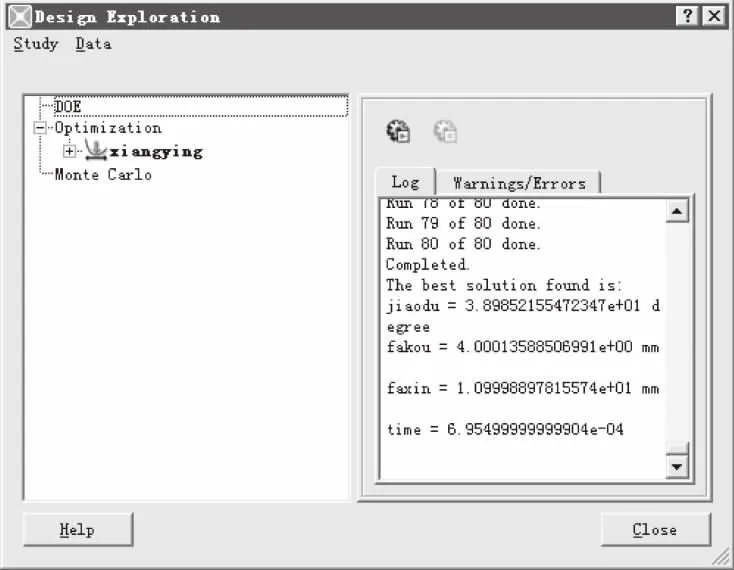
图18 多参数优化结果

3.3 单参数和多参数优化结果的比较

通过以上分析可以看出，基于遗传算法多参数影响关系得到的音圈电机直驱式高速开关阀关键结构参数的变化趋势与单参数优化结果基本一致。而且经过多参数优化提高了音圈电机直驱高速开关阀动态性能，缩短了响应时间。将单参数和多参数的优化结果分别代入开关阀的动态仿真模型中，结果如图19所示。

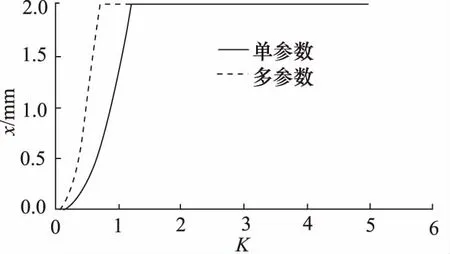
图19 经单参数和多参数优化后开关阀位移与时间关系

4 结论

为满足水下作业设备的小型化和环境相容性要求，本研究提出了一种音圈电机直接驱动的高速开关阀。通过AMESim批处理方法结合遗传算法，对比分析了不同结构参数下开关阀的动态性能，可以得出如下结论：

(1) 改变音圈电机直驱高速开关阀的关键结构参数，会对其动态性能产生较大影响。因此在实际设计与制造过程中，可以考虑通过优化关键结构来达到提升高速开关阀的动态性能的目的;

(2) 通过基于AMESim批处理的单参数影响分析得到优化后的音圈电机直驱高速开关阀关键结构参数取值如表2所示。采用该参数后开关阀的动态性能接近最佳，响应时间最短，仅需1.186 ms;

(3) 通过基于遗传算法的多参数影响分析得到优化后的音圈电机直驱高速开关阀关键结构参数取值如表5所示。采用该参数后开关阀的动态性能接近最佳，响应时间最短，仅需0.695 ms;

(4) 综上所述，基于遗传算法多参数影响关系得到的音圈电机直驱高速开关阀主要结构参数的变化趋势与单参数优化结果基本一致。而且经过多参数优化提高了音圈电机直驱高速开关阀动态性能，缩短了响应时间。