六自由度电液振动台自抗扰控制方法

(大连海事大学船舶与海洋工程学院， 辽宁大连 116000)

引言

六自由度电液振动台可以更真实的模拟被试件在实际工作环境下的动力学运动，使被试件能够快速全面的暴露其设计缺陷与安全隐患, 目前被广泛应用于国防工业领域和民用工业部门。

目前对于多轴振动台的控制策略除了常规的三状态控制策略之外，还有自适应控制、变结构滑模控制等控制策略。三状态控制策略的优势在于控制方法简单，计算量小[1]。但是该控制策略无法补偿振动台运动过程产生的扰动。自适应控制与滑模控制都属于基于模型的控制方法，这类控制策略虽然可以削弱振动台运动过程产生的扰动，但是该控制策略都要求在线计算逆动力学模型，而振动台包括多个运动链，逆动力学模型比较复杂，计算量大[2-3]。对于以上现有控制策略存在的不足，本研究提出将自抗扰控制策略运用到多轴振动台中。

自抗扰控制策略最早由韩京清[4]于1989年提出。早期的自抗扰控制器是非线性结构，所需调整参数较多，结构复杂[5-7]，这些缺陷限制了其在工业中的运用。随后高志强[8]对韩京清所做的工作进行了总结，并在其思想基础上提出了线性自抗扰控制器[9]。由于线性自抗扰控制器结构简单，所需调节的参数仅有2个，使得自抗扰控制策略在工业领域得到了广泛的应用。在电液控制领域，姚建勇[10-11]的研究成果充分证明自抗扰控制器可运用于阀控缸机构中，并取得良好的抗扰动控制效果。

六自由度电液振动台的控制精度受柔性基础与干扰力的影响。柔性基础产生的原因是基座与液压缸下端连接时存在一定的柔性，使振动台在运动时不只受液压驱动力影响，还会受到柔性连接产生的反作用力影响。干扰力的产生是受各种综合因素的影响，定义为液压驱动力与理论液压驱动力之间的偏差。

本研究在六自由度电液振动台伺服控制系统中设计自抗扰控制器，模拟振动台在受到柔性基础及干扰力影响的工作环境下，自抗扰控制器对振动台的控制效果。通过仿真结果可知，相对于三状态控制策略，自抗扰控制策略的运用可明显提升振动台的抗扰动能力。

1 六自由度电液振动台建模

1.1 六自由度电液振动台的设计指标与结构尺寸

本研究的六自由度电液振动台设计指标与结构尺寸如图1、表1所示。该六自由度电液振动台具有X，Y，Z，RX，RY，RZ6个自由度。

1.2 六自由度电液振动台机械系统模型

根据图1所示，可基于SimMechanics的机械系统动力学建模建立六自由度电液振动台模型,具体建模方式可参考文献[12]。

本研究1号液压缸支座刚度较小， 平台运动过程中将受到柔性基础扰动影响。故在1号阀控缸机构液压缸下端与液压缸支座之间添加弹簧模块，模拟柔性基础，模型如图2所示。

图1 六自由度电液振动台结构

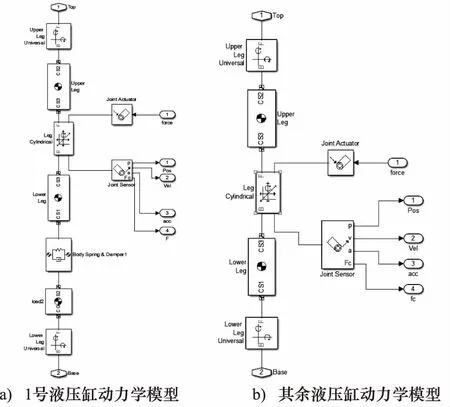
图2 基于SimMechanics的液压缸动力学模型

表1 六自由度电液振动台设计指标与尺寸结构

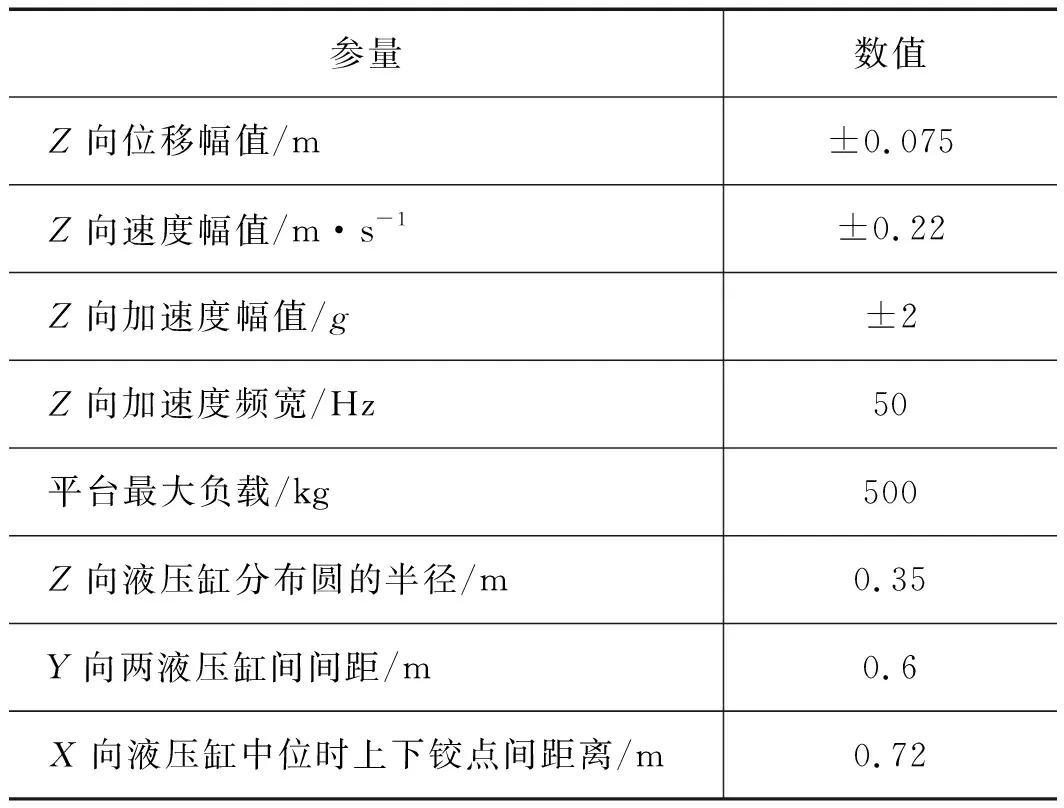
参量数值Z向位移幅值/m±0.075Z向速度幅值/m·s-1±0.22Z向加速度幅值/g±2Z向加速度频宽/Hz50平台最大负载/kg500Z向液压缸分布圆的半径/m0.35Y向两液压缸间间距/m0.6X向液压缸中位时上下铰点间距离/m0.72

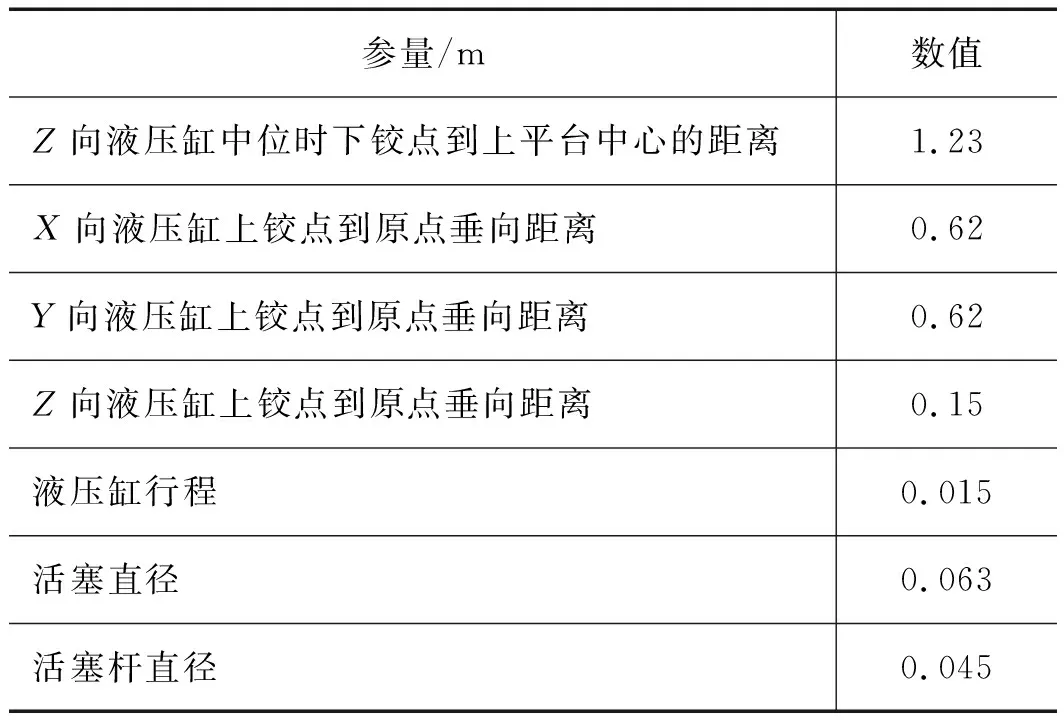
(续表1)

2 自抗扰控制器设计

在Simulink中搭建六自由度电液振动台的自抗扰控制器，其控制系统的原理如图3所示。

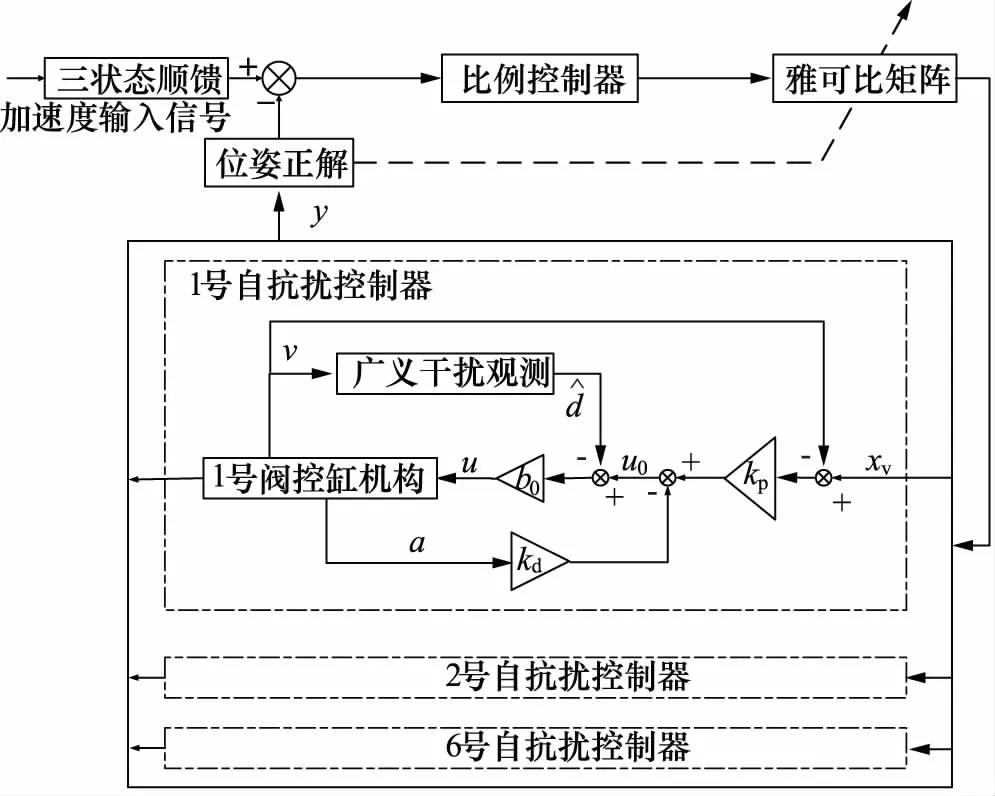
图3 六自由度电液振动台控制系统原理图

通过三状态顺馈模块将输入系统的加速度信号转换为位姿信号，再利用雅可比矩阵将位姿信号转换为阀芯位移信号。在驱动空间分别对阀控缸机构设计自抗扰控制器，以实现系统对扰动的抵抗，最终通过位姿正解求解位姿信号实现位姿闭环，完成系统对加速度信号的控制。三状态顺馈参数的设置方法参考文献[13]。

2.1 线性自抗扰控制器

六自由度电液振动平台各自由度加速度频宽的设计指标为50 Hz，而伺服阀动态特性转折频率高于100 Hz，故可忽略伺服阀动态特性的影响。

下面以1号阀控缸机构为例，简述自抗扰控制器设计过程。

根据阀控缸机构的3个基本方程建立驱动机构的数学模型。阀控缸机构的3个基本方程分别为：

QL=Kqxv-KcpL

(1)

(2)

(3)

式中，QL—— 负载流量

Q′ —— 液压缸运动受柔性基础影响所需的额外流量

Kq—— 伺服阀的流量增益

xv—— 伺服阀的阀芯位移

Kc—— 伺服阀的流量压力系数

pL—— 液压缸两腔压降

A—— 活塞有效面积

y—— 活塞杆的位移

Ct—— 液压缸的总泄漏系数

Vt—— 液压缸2个腔室的总容积

βe—— 等效体积弹性模数

mt—— 铰点空间等效单缸质量

根据式(1) ～式(3)可得阀控缸机构的液压缸活塞杆速度v与阀芯位移之间的微分方程为：

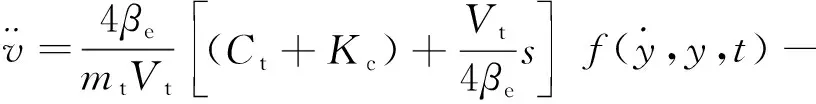
(4)

定义广义扰动为：

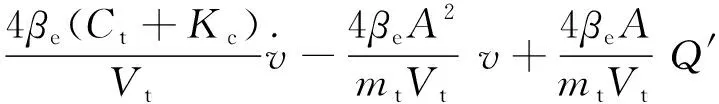
(5)

根据式(5)，阀控缸机构的状态方程为：

(6)

整理得：

v=Cx

(7)

式中，

广义干扰观测器的结构为：

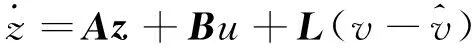
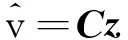
(8)

C=[1 0 0]z=[z1z2z3]T

式中，L为广义干扰观测模块的反馈矩阵；设干扰观测模块的观测极点为λ0，则矩阵L的系数为：

(9)

(10)

控制器可取为：

u0=kp(xv-v)-kda

(11)

设控制器的极点为ωc，则：

(12)

2.2 运动学正解与雅可比矩阵

运动学正解模块与雅可比矩阵模块的作用是实现六自由度电液振动平台的位姿空间信号与驱动空间信号的相互转换。

为描述平台的运动，在平台的控制点O构建静坐标系与体坐标系。坐标系具体建立方式可参考文献[12]。

根据图1设平台处于中位时上铰点在体坐标系下的齐次坐标矩阵为A，下铰点在静坐标下齐次坐标矩阵为B，由静坐标系到体坐标系的变换矩阵为T[13]。以此求得上铰点A在静坐标系下的齐次坐标可用矩阵G表示为：

G=[gij]=T·A

(13)

设i号液压缸活塞杆伸缩量为Li，X向与Y向液压缸中位时上下铰点间距离为Dh，Z向液压缸中位时上下铰点间距离为Dv，对于水平向3个液压缸，其液压缸伸缩量与对应静坐标系中上下铰点坐标关系为：

(14)

对于垂直向3个液压缸，其液压缸伸缩量与对应静坐标系中上下铰点坐标关系为：

(15)

令：

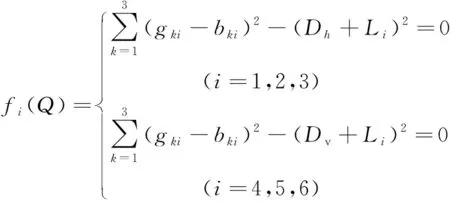
(16)

上式是关于Q的一个非线性方程组，求解过程既为运动学正解，该非线性方程组可用Newton-Raphson迭代法求解[14]。

J为雅可比矩阵，J为：

J(q)=[lT(TA×l)T]

(17)

式中，l=[l1,l2,…,l6]，li为i号液压缸在单位方向上的矢量。

3 仿真分析

本研究分别通过X自由度的位姿阶跃响应、加速度正弦运动及频率特性仿真分析，检验自抗扰控制策略的有效性，仿真主要参数如表2所示。

图4为阶跃响应仿真曲线。输入幅值为0.01 m的阶跃信号，分别采用三状态控制策略与自抗扰控制策略对平台进行控制。表3所示为阶跃响应主要性能指标。由表3可知，应用自抗扰控制策略，明显改善了控制系统阶跃响应指标。

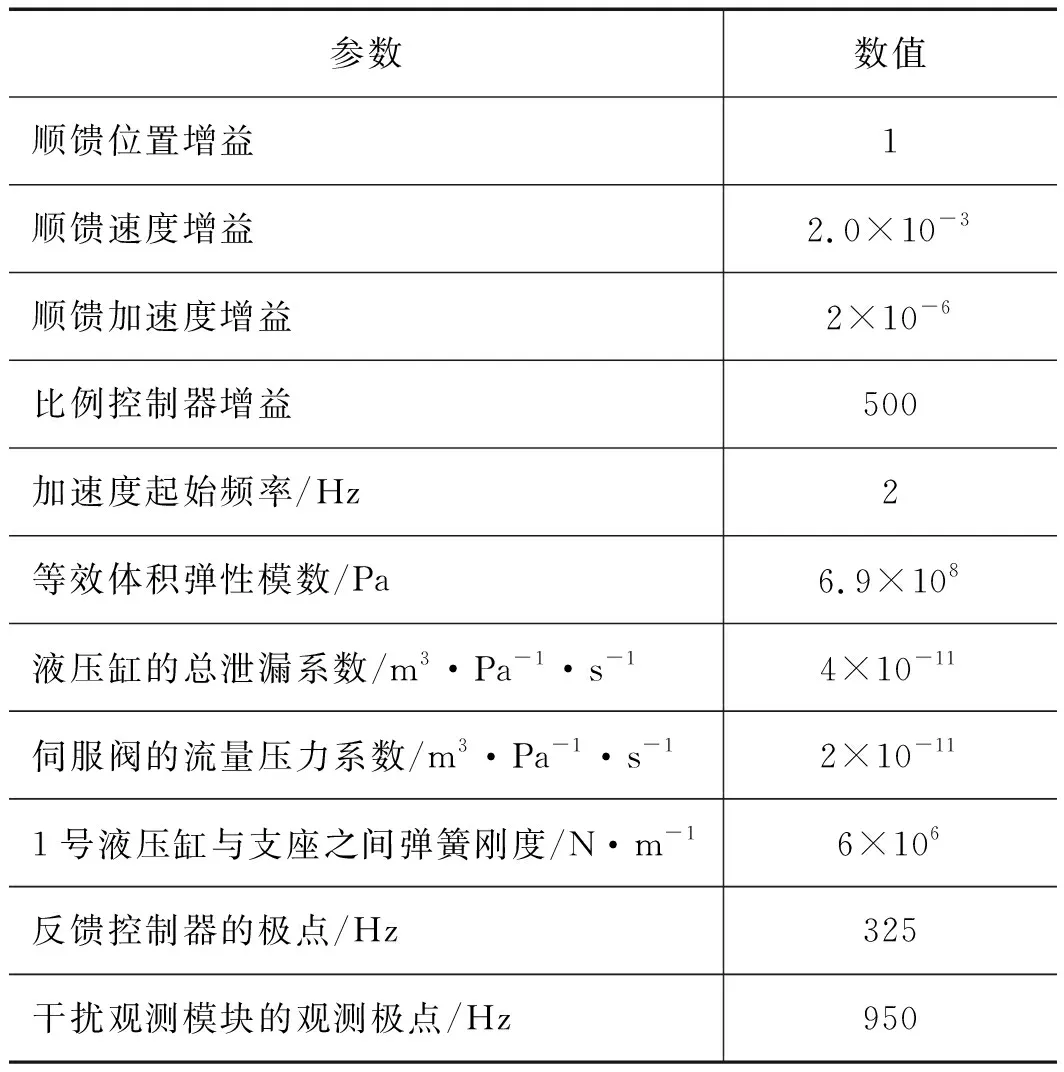
表2 六自由度电液振动台的仿真主要参数

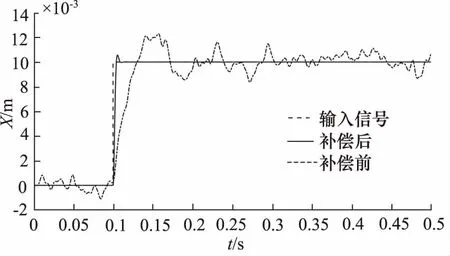
图4 X自由度位姿信号阶跃响应

表3X自由度位姿信号阶跃响应主要性能指标

性能指标三状态控制策略自抗扰控制策略上升时间0.03 s0.005 s超调量25%7%调整时间0.3 s0.02 s

图5为X自由度加速度正弦运动仿真曲线，输入信号频率为15.7 Hz，幅值为1g的正弦信号，由图可知，较补偿前，进行补偿之后的系统所输出正弦曲线的衰减减弱，跟踪特性更精确。

图6为X自由度加速度频率特性仿真曲线，由图6可知，采用三状态控制策略时，X自由度加速度幅频特性曲线存在明显的波峰波谷，在10～20 Hz频段之间出现了约20 dB的波动。采用自抗扰控制器时，该频段内的波动消失。

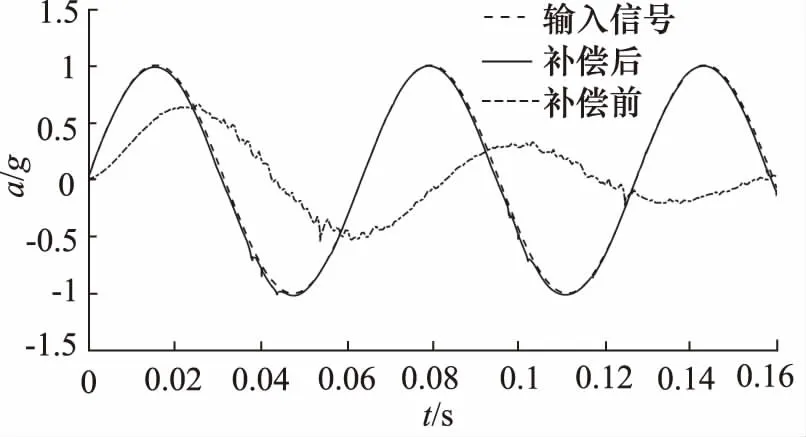
图5 X自由度加速度正弦跟踪曲线

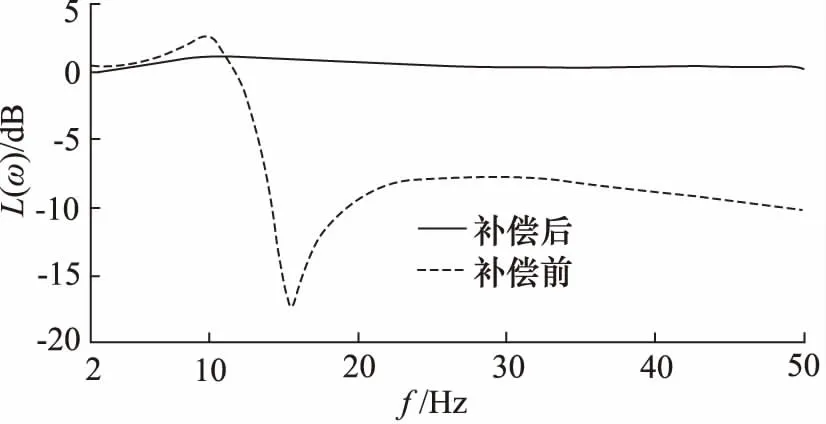
图6 X自由度加速度频率特性曲线

4 结论

本研究针对振动台的控制精度受柔性基础及干扰力影响的情况，提出将自抗扰控制器运用到振动台控制系统中。

在Simulink中建立六自由度电液振动台的模型，对其阀控缸机构分别设计自抗扰控制器后，结合三状态顺馈、位姿正解与雅可比矩阵设计出平台加速度控制系统。通过X自由度的位姿信号阶跃响应、加速度正弦运动与幅频特性的仿真结果表明：自抗扰控制策略运用到电液振动平台控制系统中可有效的抵抗因柔性基础引起的加速度幅频特性中存在的波峰波谷，提升系统的控制精度。

考虑到本振动台的加速度设计频宽未超过50 Hz，本研究未考虑伺服阀的动态特性。若进一步提升振动台的性能，要求加速度频宽超过100 Hz时，应考虑伺服阀的动态特性，增加自抗扰控制器的阶数，对此有待更进一步研究。