基于AMESim的阀芯回转式液压激振器的动态特性研究
(江西理工大学机电工程学院, 江西赣州 341000)
引言
激振器是一种附加在某些机械和设备上产生激励力的部件,常应用在岩石破碎、道路桥梁、航空航天等领域[1]。液压激振器是液压激振技术应用的关键元件,以滑阀控制和转阀控制的液压激振器最具有代表性。随着现代科技的发展需要,研制出高效率、高频率、高负载的激振器具有重要意义[2]。
龚国芳等[3-4]提出一种不同开口形状的阀芯旋转式激振器,对振动波形理论分析和实验研究得到了阀芯旋转过程中的液动力分析和补偿措施。阮键等[5-7]研发出新型2D阀控液压激振器,通过阀芯轴向运动改变过流面积,实现对频率和振幅的调节。郝建功等[8]发明了一种新型阀芯旋转式电液激振器,利用阀芯的旋转运动,使得液压缸的无杆腔的压力在高压与零之间不断变化,从而实现活塞杆的往复运动。赵国强等[9]提出一种旋转式激振阀,设计了三种不同阀口,对不同阀口流场进行动态模拟及实验研究,为激振阀阀口优化提供了理论基础。
本研究设计了一种新型阀芯回转式液压激振器,利用电机带动阀芯旋转,具有更好的调节工作频率的能力;负载对激振效果影响较小,能实现高负载作业。通过对激振器结构及激振过程进行相关介绍,建立液压激振器系统的数学模型;对阀控缸系统进行AMESim仿真分析,得到激振器的动态特性曲线。
1 液压激振器结构
本研究提出的阀芯回转式液压激振器结构如图1所示,主要由阀芯、阀体、轴承、端盖、密封圈等组成。阀芯沿着径向方向开有2个直孔阀口与2个斜孔阀口,四孔不相交,四孔所处的平面为一个平行状态,每一个相邻油口之间的角度为90°,且阀体纵截面上开有与阀芯相匹配的油口,保证了油液的通断与切换。阀芯旋转由伺服电机带动,通过调节电机的转速来控制阀芯的转速。
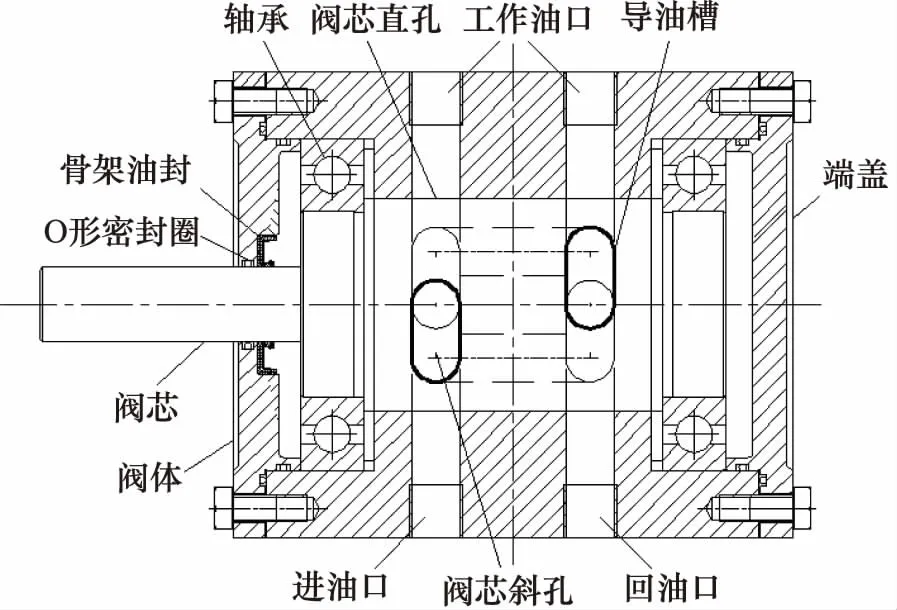
图1 阀芯回转式液压激振器结构示意图
液压激振器工作原理如图2所示。标记阀芯的直孔阀口为阀口I、阀口Ⅱ;斜孔阀口为阀口III、阀口IV。当阀芯直孔起作用时,液压油依次流入油口P、阀口I及连接液压缸的油口A,最后通过高压油管进入液压缸的左腔,此时左腔压力大于右腔,油压作用于A1的活塞面,通过活塞推动负载向右运动。同时右腔油液由于受到活塞运动的作用,依次经过油口B、阀口Ⅱ和回油口T流入油箱。当斜孔起作用时,高压油液由油口P进入,流入阀口III通过连接液压缸的油口B进入到液压缸右腔,右腔压力大于左腔压力,压力作用于A2活塞面,推动活塞带动负载向左移动。左腔高压油受到活塞作用,通过油管依次从油口A、阀口IV、出油口T流入油箱。利用这种连接方式,阀芯每旋转180°液压缸左腔和右腔进出压力油完成一次交替变换,阀芯旋转驱动活塞来回往复运动。
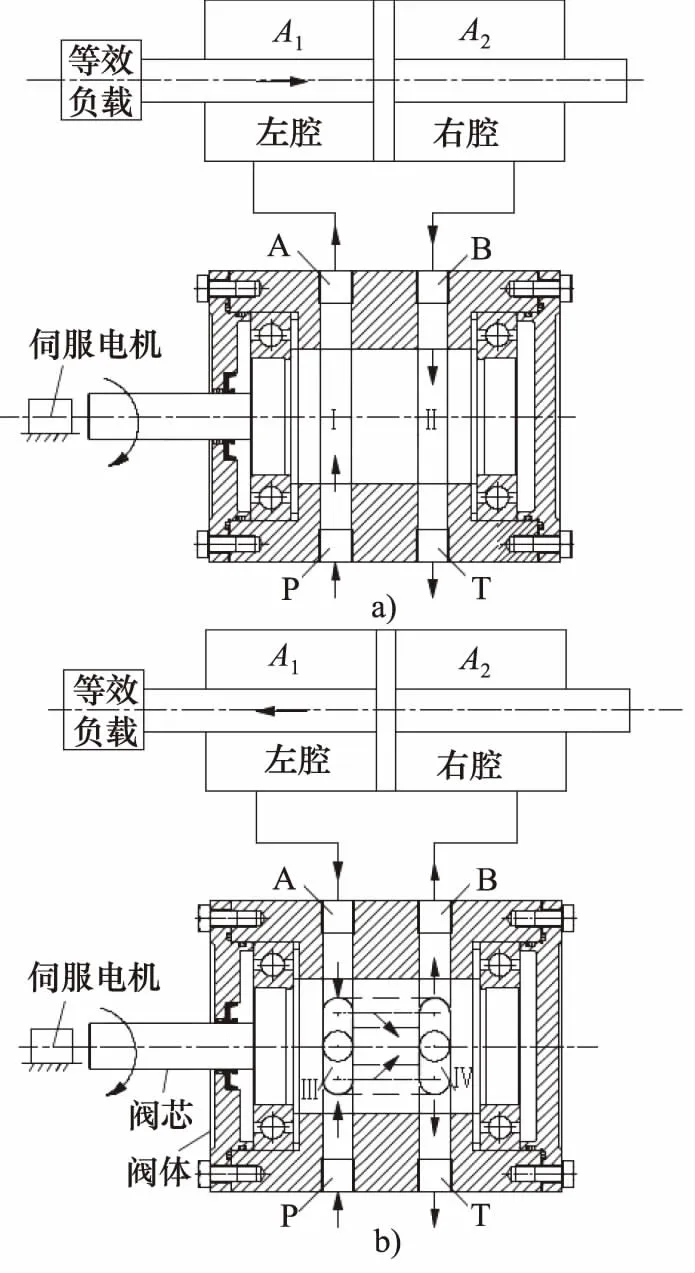
图2 阀芯回转式液压激振器
2 液压激振器的数学模型
2.1 阀口面积的数学模型
转阀的阀口面积示意图如图3所示,当转阀高速旋转时,阀芯沟槽与阀体沟槽配合会形成一个重合部分,该重合区域面积为阀口开度面积。对于图3b的转阀过流面积模型,其中实线代表阀体的过流面,虚线为可动区域代表阀芯过流面,阴影部分为阀芯旋转角位移为Rθ时的过流面积,其面积的计算公式为式(1):
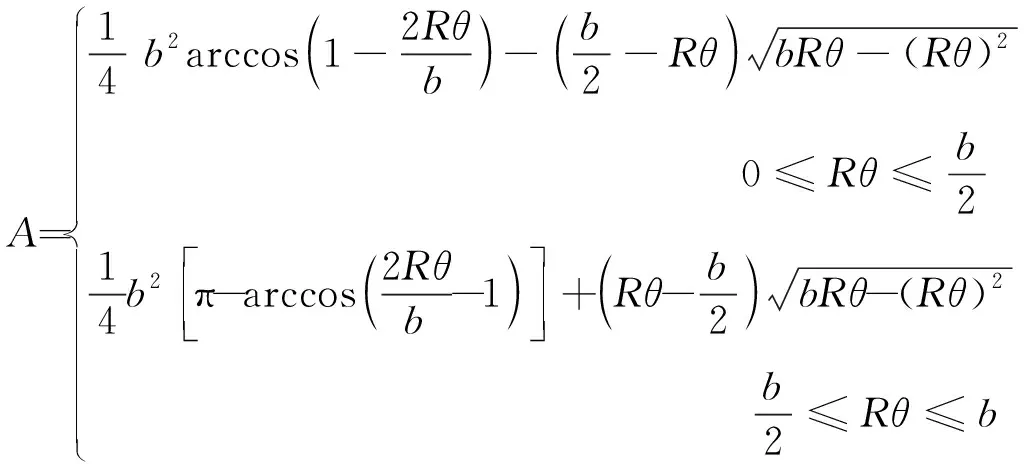
(1)
b=Rα
(2)
式中,R—— 转阀阀芯的半径
α—— 阀芯开口的最大角度
θ—— 阀芯角位移
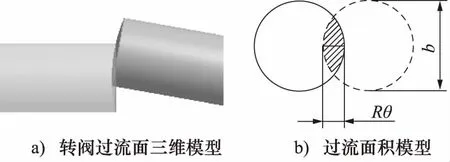
图3 转阀节流面过流面积模型
将式(2)带入式(1)得式(3)。当转阀在正常工作时,对任意阀口处于流通状态时,有4个阀口处于通油状态,所以其阀口过流面积理论计算公式为式(3):
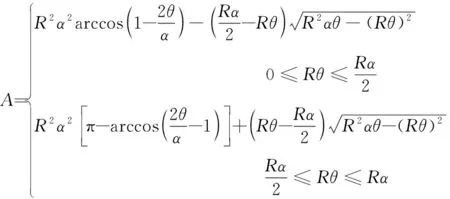
(3)
2.2 转阀的工作频率
通过分析可知,阀芯由电机带动做连续旋转时,随着阀芯高速旋转,直孔与斜孔不断交替切换,进而实现往复换向运动。其工作频率计算见式(4):
(4)
式中,m—— 阀芯与阀体的导通次数
n—— 电机转速,r/min
由式(4)可知,工作频率与电机转速n和阀口单个周期导通的次数m有关。本研究所述的伺服阀在阀口数量上是定值,工作频率可以通过电机转速来改变。与传统的伺服阀比,有更好的调节工作频率的能力,并且可以保证较大的推力特性。
2.3 激振系统等效液压桥梁
根据阀芯回转式液压激振器工作原理,将阀芯控制液压缸组合建立等效液压桥路如图4所示。在求解方程的过程中进行适当的简化,给出如下假设:液压油为理想液体,只考虑稳定的工况下,弹性模量不变,温度不随工作状况改变,液压缸2端不存在压差。液压缸两腔的压力分别为p1和p2。那么压降pL与pS计算公式分别为式(5)、式(6):
p1-p2=pL
(5)
p1+p2=pS
(6)
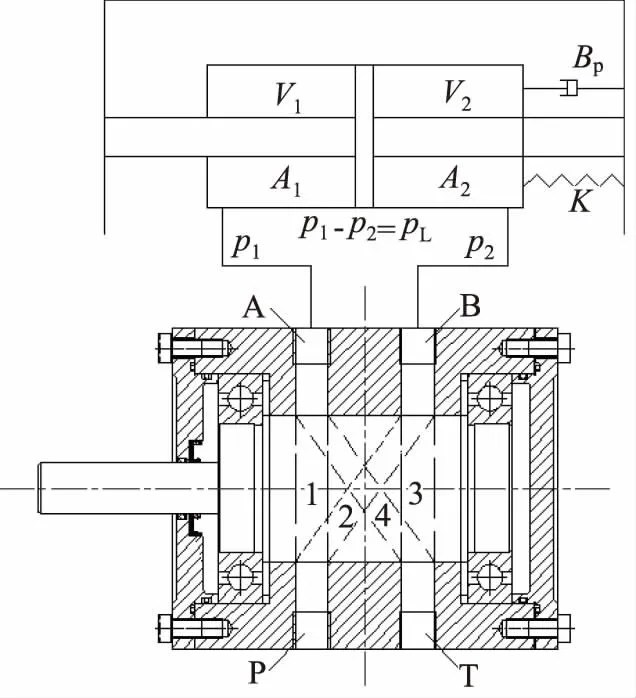
图4 激振系统等效液压桥路
在直孔作用时,即油口P和油口A联通,油口B和油口T联通时伺服阀的流量方程为式(7);当斜孔作用时,即油口P和油口B联通,油口A和油口T联通时伺服阀的流量方程为式(8)。
(7)
(8)
式中,Q1,Q2,Q3,Q4—— 依次为对应的4个阀口的流量
Cd—— 流量系数
Ai—— 分别对应的4个阀口面积
ρ—— 液压油密度
假定液压缸内部没有泄漏,则液压缸流量连续性方程为式(9),动力学方程为式(10):
(9)
(10)
式中,β—— 液压缸中液体的体积弹性模量
V—— 液压缸两腔的总体积
m—— 活塞与负载的总质量
Bp—— 黏性阻尼系数
K—— 负载弹性刚度
FL—— 负载力
yp—— 活塞的位移
Ap—— 活塞的面积
3 AMESim模型的建立
根据上述液压激振器的结构、工作原理及系统的数学模型,建立仿真模型。在AMESim中利用功能一样的滑阀替代[10-11],将转阀的阀口面积变化规律替换为滑阀阀口面积的变化规律[12],模型如图5所示,仿真参数如表1所示。
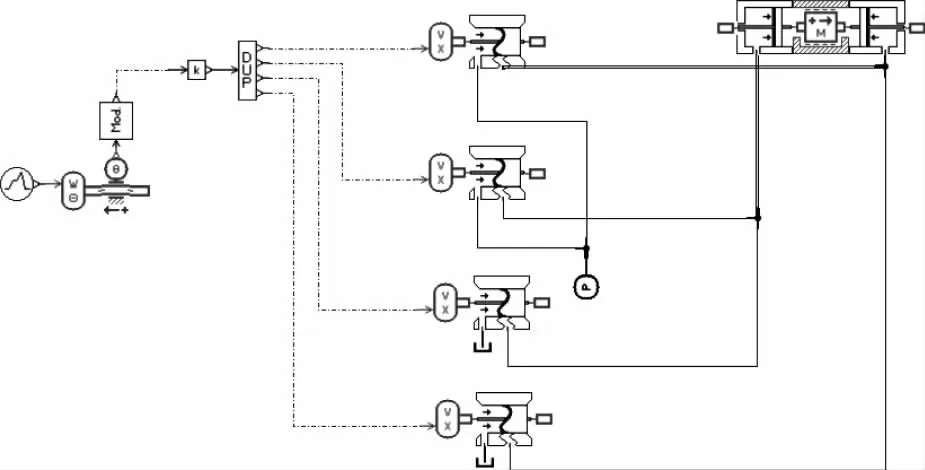
图5 系统的AMESim模型
表1 AMESim仿真参数
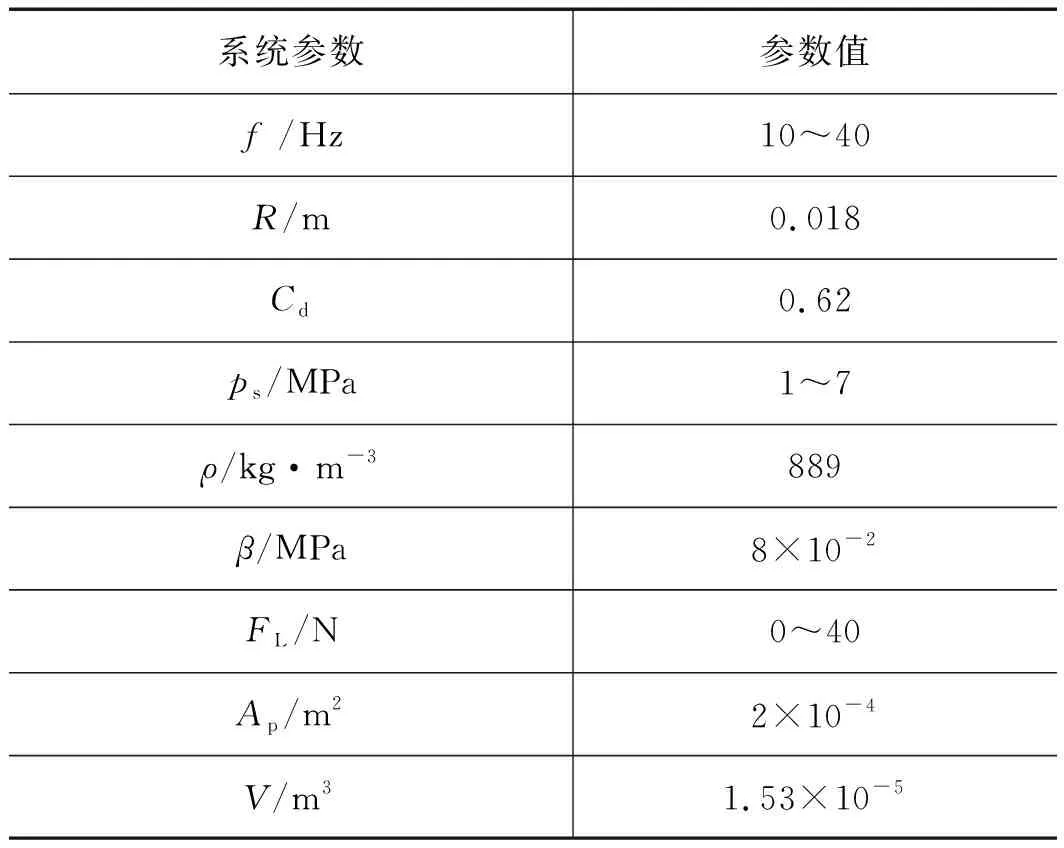
系统参数参数值f /Hz10~40R/m0.018Cd0.62ps/MPa1~7ρ/kg·m-3889β/MPa8×10-2FL/N0~40Ap/m22×10-4V/m31.53×10-5
4 仿真结果与分析
通过仿真得到阀芯回转式液压激振器在供油压力为2 MPa,负载质量为200 kg,阀芯转速分别为600, 1200, 1800, 2400 r/min,即频率为10, 20, 30, 40 Hz时液压缸活塞输出的位移、速度、加速度以及激振力曲线,分别如图6a~图6d所示。
由图6a可知,液压缸活塞位移变化曲线呈梯形脉冲变化。当供油压力一定时,其位移峰值随着阀芯转速的增大而降低,但是同等时间内的激振次数增多。产生的原因是因为转速增大,阀芯与阀体导通的次数增多,阀口配合的时间减小,从阀口流入的流量减小,进而导致活塞位移峰值降低,激振频率增大。由图6b可知,当系统供油压力恒定时,随着转速的增大, 速度增量增大,但速度峰值基本保持一致,约为0.26 m/s。因阀口面积一致,速度峰值是由阀口全开时的流量大小决定,所以峰值不随转速增减发生变化。由图6c和图6d可知,当供油压力一定时,其加速度和激振力的峰值均随着阀芯转速的增大而增大。加速度变化曲线波动比较明显,当频率为40 Hz时,加速度峰值可达115 m/s2。当频率增大激振力出现越快,在频率越低时出现越慢;在频率为40 Hz时候激振力达到最大值约为42.5 kN。
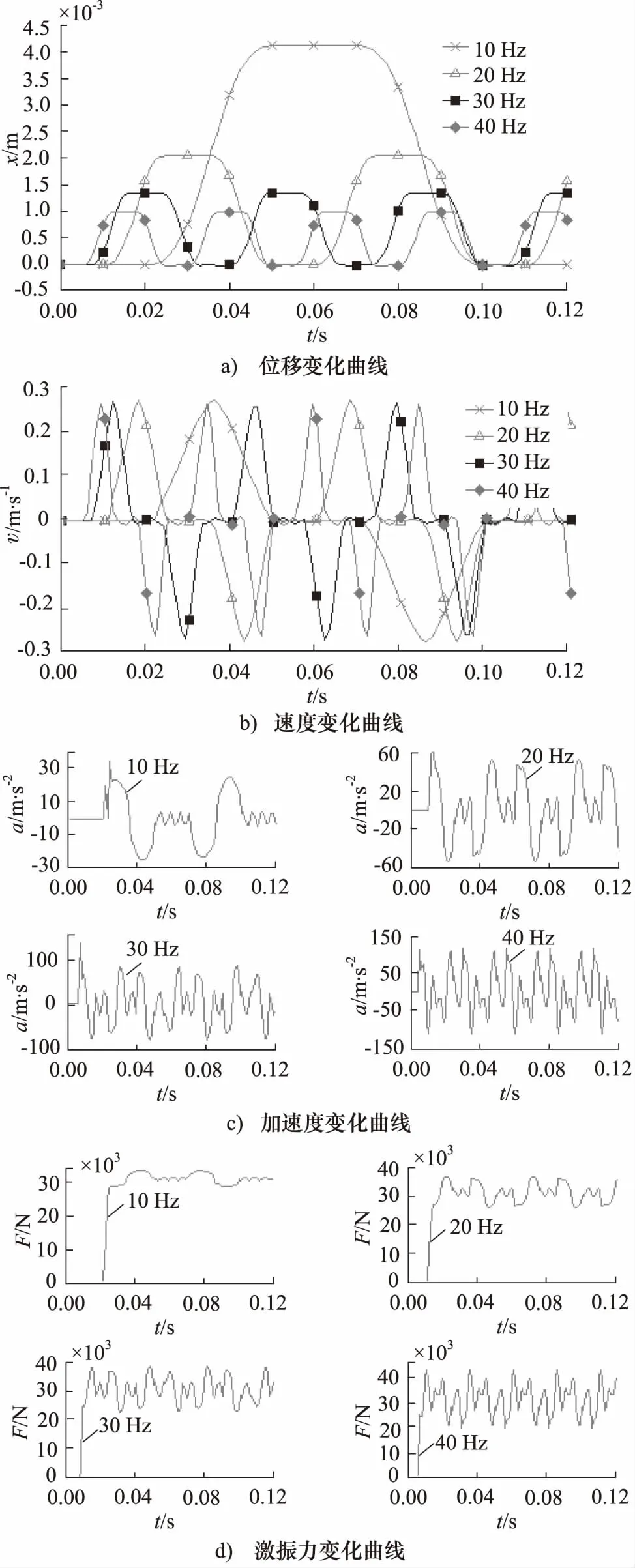
图6 阀芯转速对系统动态特性影响曲线
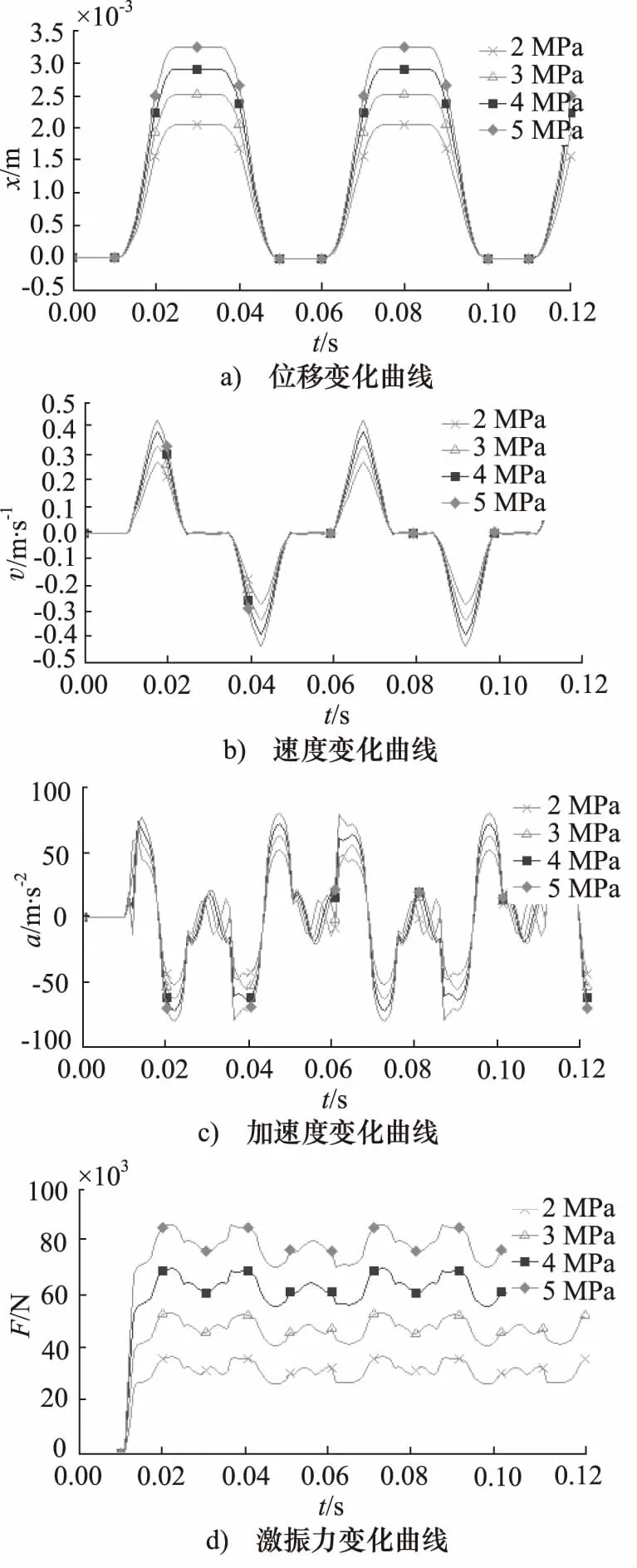
图7 不同油压对系统动态特性影响曲线
图7为阀芯回转式液压激振器在工作频率为20 Hz、负载质量为200 kg的工况下,供油压力分别为2~5 MPa时,对液压缸活塞的位移、速度、加速度、激振力的影响曲线。
由图7a可知,在阀芯工作频率恒定时,供油压力由2 MPa增大到5 MPa时,位移峰值从2.04 mm增大到3.24 mm。因压力升高,其转阀阀口的压降现象增大,通过阀口的流量增多,进而位移峰值增大。由图7b可知,液压缸活塞的速度随着供油压力的增大而增大,曲线呈现叠峰现象。供油压力从2 MPa增大到5 MPa 时,其速度峰值增长迅速,由0.27 m/s增至0.434 m/s。由图7c可知,加速度随着供油压力的增大而增大。在初始时刻,不同供油压力下其加速度均出现了波动情况,随之趋于稳定状态,加速度曲线存在明显的“双峰”现象,压力为5 MPa的工况下,出现最大加速度79.5 m/s2。由图7d可知,激振力随供油压力增大而增大,在供油压力为5 MPa时达到最大值86 kN。
由以上分析可知,液压缸活塞的位移、速度、加速度、激振力与供油压力呈现正相关性。同时阀腔内的负压区域也会增多,容易引发噪声和气穴现象,进而影响工作性能。因此,在实际工作当中,对压力的选择应充分考虑各种因素,以选择最合适的压力,得到最好的效果。
图8为阀芯回转式液压激振器在工作频率为20 Hz、系统供油压力为4 MPa的工况下,不同负载质量对液压缸活塞的位移、速度、加速度和激振力的影响曲线。随着负载质量的增大,活塞的位移、速度、加速度、激振力的峰值均发生变化,但变化量不明显,故对曲线图进行局部放大,各项峰值数据如表2所示。
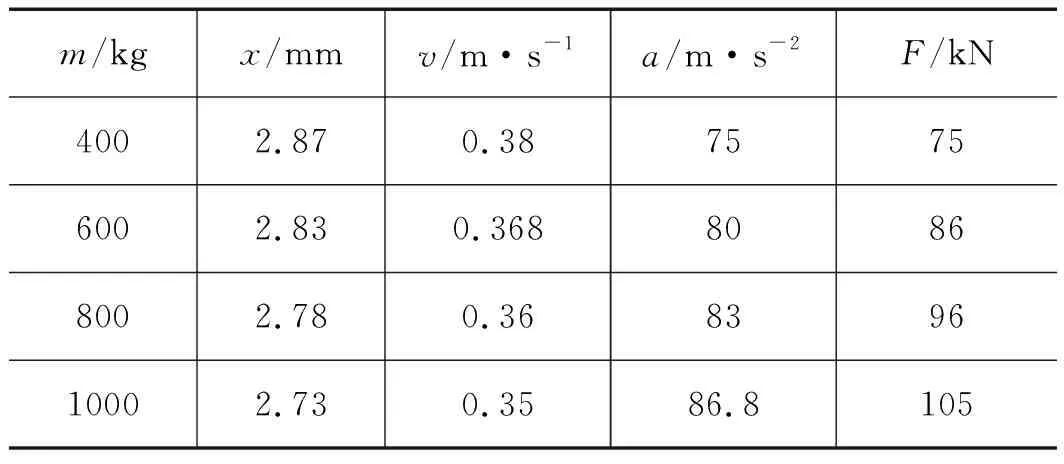
表2 不同负载质量下各变量的峰值
由图8a和图8b可知,负载质量由400 kg增至1000 kg时,位移峰值和速度峰值均减小。位移峰值由2.87 mm减小到2.73 mm,速度峰值由0.38 m/s减小到0.35 m/s。总体减小幅度较小,且趋势相同。由图8c和图8d可知,负载质量增大对应加速度峰值和激振力峰值均随之增大。加速度峰值由75 m/s2增大到86.8 m/s2,激振力峰值从75 kN增大到105 kN。加速度曲线存在“双峰”现象,并且在初始位置同样发生了加速度突然增大的情况。因在电机刚启动带动阀芯旋转时,由于负载效应,会产生一定的压力波动,这种波动会增加液压激振系统的不稳定性。
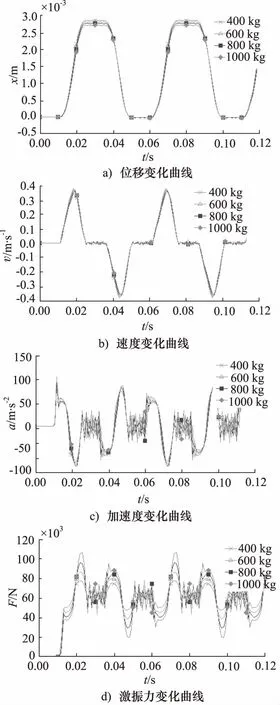
图8 不同负载质量对系统动态特性影响曲线
5 结论
从整个阀控缸系统的角度出发,对阀芯回转式液压激振器的动态特性进行分析,通过对转阀的结构研究、数学模型的建立及AMESim仿真结果分析,得到阀芯频率、供油压力以及负载质量对其激振性能的影响。结果表明:
(1) 提高阀芯的转速,振幅幅值随之减小但同时间内激振次数增加,对速度的峰值影响较小,加速度和激振力随之增大;
(2) 液压缸供油压力的提升,对振幅幅值、速度、加速度和激振力均起到增大作用;
(3) 压差、频率一定的工况下,随着负载质量的增加,其振幅峰值和速度随之减小,加速度和激振力随之增大,但激振过程整体变化不明显。此液压激振器负载质量对激振效果影响较小,为完成高负载作业提供理论指导。

