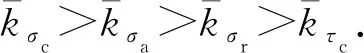基于ALE流固耦合作用的管道车静止于不同流量管流时壁面应力的分布
杨小妮,马娟娟,李永业,孙西欢,2
(1.太原理工大学 a.水利科学与工程学院,b.现代科技学院,太原 030024;2.晋中学院,山西 晋中 030600)
管道车水力输送是继浆体管道输送方式和型料管道输送方式之后的一个全新的管道水力输送方式。管道车水力输送最早于20世纪60年代在加拿大阿尔伯塔省研究委员会提出[1]。之后得到美国国家自然科学基金的支持,在密苏里哥伦比亚大学建立了一个管道车水力输送系统研究中心。在该中心对管道车水力输送进一步研究和开发。管道车在管流中主要存在两种状态:静止和运动。在20世纪中后期首先对静止于管流中的管道车做了大量研究。由于所有的管道车水力输送系统都存在偶尔启动和停止[2-3],因此研究静止于管流中的管道车的情况有很重要的意义。1981年,LIU et al[2]具体介绍和定义了管道车水力输送系统的概念,并通过测量静止于管流中管道车周围的压力分布,确定了管道车的升力和阻力系数。之后通过理论推导得出静止于管流中管道车沿程压力的分布情况,并将该理论应用于单个管道车的管底阻力、端部压力系数和初始速度的预测中[3]。GAO et al[4]将LIU and RICHARD推导的单个管道车初始启动速度进一步修正,并且适用于管道列车。孙西欢等[5]对管道车在管流中的启动条件进行了试验研究。井元昊等[6]研究了管道车和管道之间环状缝隙流的水力特性。
对于运动状态的管道车,早在20世纪中期就有学者开始研究。KROONENBERG[7]通过理论推导得出管道车的平均速度及其两端的压降变化情况,并对其进行了试验的验证。CHARLES[8]分别估算了同心环状缝隙流为层流和紊流两种状况下的管道车的运行速度及缝隙流的速度,并对这两种流态条件下的管道车的运行速度和管流的平均速度进行比较,得出管道车的运行速度总是超过管道流体的平均速度。TOMITA et al[9]在管道车上建立动坐标系,通过理论推导也得出管道车的运行速度总是大于水流的平均速度,并进行了物理试验验证。LATTO和CHOW[10]讨论了不同缝隙比对速度比Rv、压降比Rp以及单位能量损失的影响。MICHIYOSHP和NAKAJIMA[11]根据Reichardt的动量涡扩散系数表达式和Nikurads的圆管混合长度表达式,计算了缝隙流的速度分布、摩擦系数以及管道车两端牛顿流体的混合长度和涡流扩散系数。NOURI et al[12]通过试验测得同心环状缝隙流的流体速度、雷诺应力等情况。进入21世纪,随着计算机技术的日臻成熟,推动了计算流体力学(CFD)领域进一步发展。QUADRIO[13]首次利用N-S方程采用数值模拟的方法模拟了管道车周围缝隙流场的水流特性;KHALILet al[14]分别利用三种模型(Baldwin-Lomax model、k-eandk-w)对管道车周围缝隙流场进行数值模拟和结果对比。ASIM et al[15]通过CFD模拟了不同缝隙宽度和长度的压降变化情况。李永业等[16]和张春晋等[17]分别对不同型号管道车在管道中运移时的流场特性进行了试验研究和数值模拟。
但无论是物理试验还是数值模拟,位于管流中的管道车流体对其壁面的应力分布情况鲜有研究。仅有少数学者仅有少量简单理论的阐述。
管道车水力输送过程中涉及流固耦合力学,在水流推动管道车运输的过程中,水流作用于管道车的荷载会使管道车产生形变,而管道车的形变也同时作用于水流,水流会发生变化。因此,在该模型的建立时采用双向流固耦合。对于解决流固耦合的问题,有很多不同的方法,例如Immersed Boundary Method (IBM),Lattice Boltzmann Methods (LBM) and Arbitrary Lagrangian-Eulerian (ALE) method[18].本模型采用任意拉格朗日—欧拉法(Arbitrary Lagrangian-Eulerian technique,简称ALE)进行求解。任意拉格朗日-欧拉(ALE)方法基于参考点的任意移动,伴随着一个好的“网格移动算法”,被用作移动网格类型的解算器,该解算器通过结构的运动重建网格,使我们能够相当方便地处理移动边界、自由表面和大变形以及界面接触问题,而且精度很高[19-20]。
本文采用Comsol Multiphysics 5.4软件对管道流体域和管道车固体域进行联合求解,探究管道车静止于管流中流体对其壁面的应力分布情况,并通过模型试验进行验证,以期对进一步完善相关理论提供一定的参考。
1 材料与方法
1.1 管道车结构
管道车水力输送是将物料密封于圆筒状容器(管道车)当中,然后注入循环封闭管道,以水流作为载体,水压力提供动力,将物料输送到指定目的地的一种新型的输送方式。本次试验所用管道车模型示意图如图1所示,主要由料筒、密封盖和支脚三部分组成[6,16-17]。料筒作为管道车的核心部件,用于盛放需要运输的物料,Lc表示料筒的长度,150 mm;Dc表示料筒的外径,80 mm;料筒壁厚5 mm.支撑体上安装有支脚,呈120 °角分布,保证了管道车在运行过程中与管道同心,支撑体端部装有万向滚珠,用来减少管道车在运行过程中与管壁的摩擦。
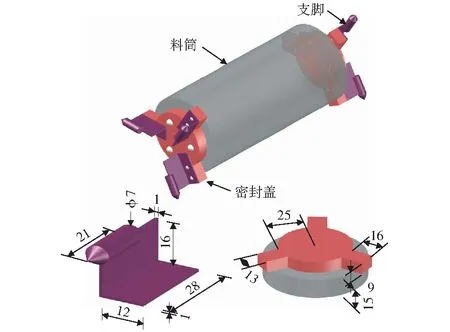
1-料筒;2-密封盖;3-支脚图1 管道车结构示意图(单位:mm)Fig.1 Structural sketch of piped carriage(unit:mm)
1.2 试验系统
图2是试验的管道系统图,管道系统由壁厚为5 mm的有机玻璃管、15 mm厚的有机玻璃法兰盘、电磁流量计、投放装置和接收装置组成[17]。管道车通过前后两个直径为2 mm的螺钉穿过管壁进行固定。本次试验的试验装置包括用于测量缝隙流流场的激光多普勒测速系统(LDV)和测量缝隙流对管道车壁面正应力的测力系统。
1.2.1激光多普勒测速系统(LDV)
为了测到缝隙流的三维速度,根据坐标支架的内置坐标,沿水流方向为X轴,垂直于X轴且位于同一水平面的方向为Y轴,根据右手螺旋,垂直于水平面的方向为Z轴,如图3所示。测试过程中同时使用两个激光探头,水平探头发射的绿光和蓝光分别测量X和Y方向的速度,定义为u和v;另一个探头发射的紫光测量Z方向的速度,定义为w.在试验过程中,在水中加入平均粒径为6 μm聚苯乙烯作为示踪粒子,以提高LDV的数据采集率。探头安装在可控制的支架上,仪器使用过程中测点位置通过电脑智能化控制坐标架移动。同时,通过在测试位置安装方形水套的方式来减少光的折射和散射。在信噪比中等的情况下,处理器的控制目标效率为55%.测点采用频率和实时速度由软件内置程序计算并直观显示在计算机屏幕上。
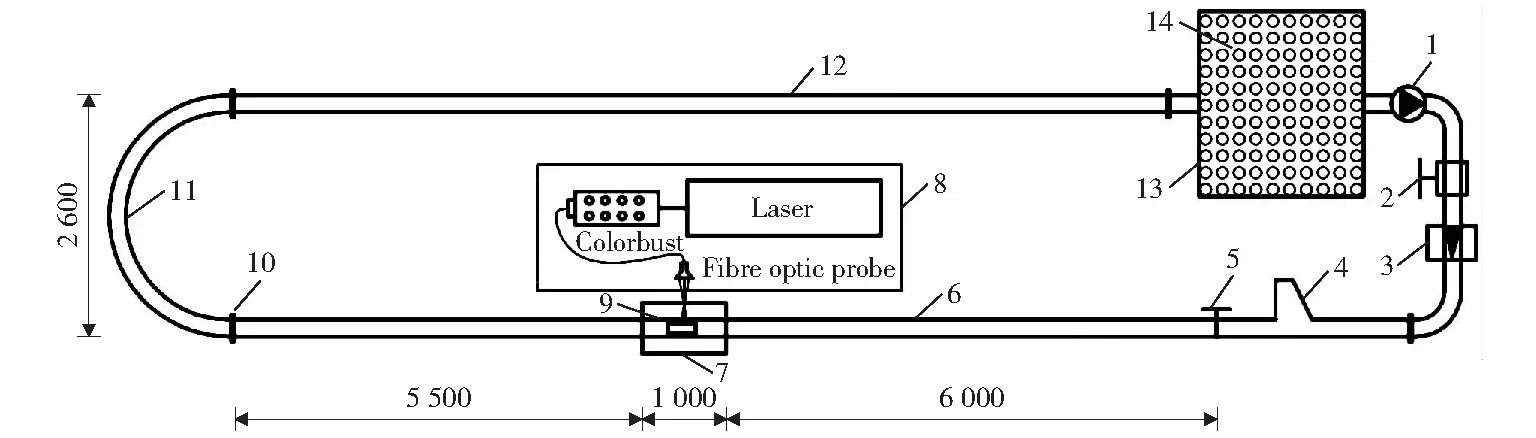
1-离心泵;2-闸阀;3-流量计;4-投放装置;5-制动装置;6-直管段;7-方形水套;8-LDV;9-管道车; 10-法兰;11-弯管;12-直管段;13-水箱;14-稳流栅板图2 试验系统结构图(单位:mm)Fig.2 Layout sketch of experiment facilities(unit:mm)
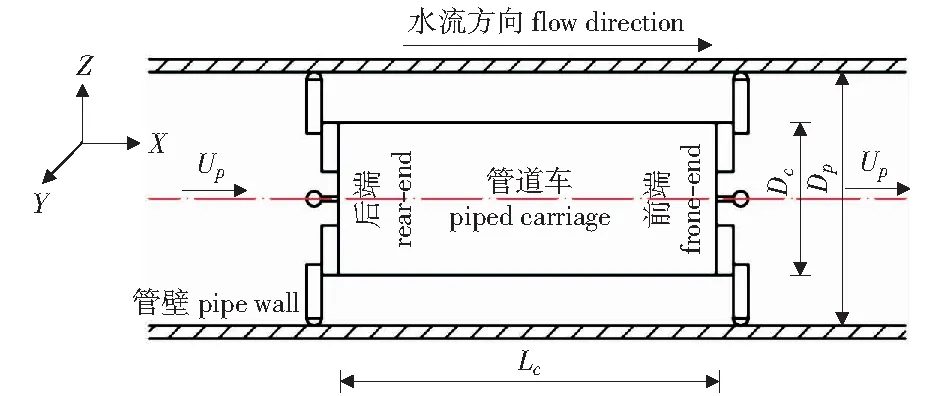
图3 管道车运输系统坐标系Fig.3 System of piped carriage coordinate
1.2.2TST5925C管道车测力系统
TST5925C管道车测力系统为一款定制的专为测试管道车车体受力的应力变化测试系统。测试系统由三部分组成:管道车测力系统主机、管道车测力系统网关、系统软件TSTDAS V5.0,如图4所示。仪器具有8个测量通道,每个通道具有独立的调理电路,独立的24 bits ADC,保证了每个测量通道具有较高的信噪比、通道之间的隔离度及每个通道并行同步采集;仪器内置了大容量存储器,实现了管道车在管道里的离线采集;仪器采用ZigBee无线传输,方便了系统的使用;仪器内置了锂电池,解决了现场工作的供电问题;仪器具有直观的工作状态指示;仪器内置于管道车中,量程为±15 000 με,分辨率为1 με,测量精度为±0.3%FS±1 με,每个通道的采样频率选用256 Hz.
测力系统放置于管道车内,与固定于管道料筒的直角应变花连接。试验所用直角应变花的型号为BX120-3CA,电阻值为119.8±0.3 Ω,灵敏度为2.08±1%.用优化方法确定直角应变花的贴片的最佳位置为贴片的定位基准是45 °片的中点,且该片与管道车的轴线平行,这种贴片定位方案可以使直角应变花的固有测量误差最小[21]。

1-管道车测力系统主机;2-管道车测力系统网关;3-系统软件TSTDAS V5.0; 4-方形水套;5-LDV探头;6-坐标架图4 试验装置和设备Fig.4 Experimental devices and instruments
1.3 断面选择及测点布置
管道车位于距离制动装置5.5 m,距离弯管入口6.0 m处,满足平稳的水流条件[22-23]。
1) LDV测量管道车料筒壁面附近流场时测点布置。
沿水流进入管道车的方向共布置32个测试断面,管道车料筒前后端20 cm,每隔2 mm布置一个测试断面,中间段每隔10 mm布置一个测试断面。每个测试断沿料筒半径方向每隔30 °布置一个测点,如图5所示,并将管道车最上方定义为0 °,每个测试断面沿水流顺时针方向布置12个测点。整个料筒周围共布置384个测点,每个测点距离料筒0.1 mm.

图5 每个测试断面上的测点分布图Fig.5 Distribution of measuring points on each test section
2) 管道测力系统测量管道车料筒正应力时测点布置。
受通道数和应变化尺寸的影响,管道车料筒共布置6个测试断面,每个测试断面测点的布置方式和流场测点布置相同。因此,整个料筒共布置72个测点。
1.4 试验工况设计
管道车在管流中的壁面应力分布,对管道车水力输送有重要的意义,尤其是在管道车料筒材料选择方面。试验选择了四个流量工况,本次试验管道车的料筒材料为有机玻璃,通过Nano Indenter G-2000型纳米压痕测试系统,测得料筒有机玻璃的杨氏模量和泊松比,相关的具体设计参数见表1.

表1 试验设计参数Table 1 Summary of experimental parameters
2 数值计算
2.1 几何模型
管道及管道车的几何模型是采用AutoCAD2007软件建立的,管道及管道车的模型尺寸与物理试验的具体尺寸一致。管道内径Dp为100 mm,根据物理试验的结果,管道车车后管长150 mm,车前管长设置为1 000 mm.管道车模型选择了四个尺寸,具体参数见表1.料筒的材料为厚度5 mm的有机玻璃。管道车料筒的两端有厚度为10 mm的圆柱状密封盖,其材质也为有机玻璃,料筒和密封盖通过内外螺纹密封连接。密封盖的外部是通过支撑体和金属连接片连接的类圆柱支脚。模型中将支撑体和金属连接片进行了简化,只保留部分金属连接片,如图6(a)所示。金属连接片为厚度2 mm,长宽分别为15 mm和28 mm的铁片。类圆柱支脚由圆柱和半球两部分组成,圆柱和半球的直径为8 mm,圆柱长20 mm,其材质均为不锈钢。将AutoCAD2007软件建立的几何模型导入COMSOL Multiphysics5.4中,绝对导入容差为1×10-5.最后形成联合体。

图6 管道车模型及网格划分示意图Fig.6 Geometric model and mesh generation of piped carriage
2.2 控制方程
2.2.1流体域控制方程
根据水流流经管道车的流体特性,我们选用标准k-ε模型进行模拟,并作一些假设: 定常和不可压缩流体,不考虑热量交换,忽略重力对管道水流的影响,湍流动能k和湍流能量耗散率ε的方程如下[24-25]。并用Boussinesq方法近似计算了湍流涡动粘度μT.
湍流动能方程:
(1)
湍流能量耗散率方程:
(2)
湍流涡动粘度方程:
(3)

在管道的内壁和管道车外壁区域,水流受壁面流动条件的影响比较明显,该区域标准k-ε模型不再适应。对于该区域,我们采用壁面函数法进行求解,即直接使用半经验公式将壁面上的物理量与湍流核心区内的求解变量联系起来[25]。
2.2.2固体域控制方程
管道车料筒材料为有机玻璃,属于可压缩材料,因此固体部分的守恒方程可以由牛顿第二定律导出[26]:
(4)
其中,ρs是固体密度,σs是柯西应力张量,与第二个Piola-Kirchhoff应力有关,则σs=J-1FSFT,其中F(=I+us),J=det(F).S是第二个Piola-Kirchhoff应力张量,S=λs(trE)I+2μsE,E=(FTF-I)/2.Lamé系数λs和μs可按式(5)和(6)计算。fs是体积力矢量,as是固体域当地加速度矢量,在本研究中管道车处于静止状态,as=0.
(5)
(6)
式中:E和υs分别是有机玻璃的杨氏模量和泊松比,具体取值见表1.
2.2.3流固耦合方程
流固耦合遵循最基本的守恒原则,在管道车料筒的壁面上满足运动学条件(又叫位移协调)df=ds和动力学条件(又叫力平衡)n·τf=n·τs,其中df和ds分别表示管道水流和管道车的位移,管道车处于静止状态,则df=ds=0;τf和τs分别表示水流和管道车壁面的应力。
静止于平直管流的管道车模型属于稳态,耦合界面上流体节点的位置由运动学条件决定的。因此,水流在耦合界面的速度为零。根据动力学条件,耦合界面上的水流分布力根据公式(7)积分为集中力施加在结构节点上。
(7)
式中:hd是结构点的位移。
2.3 边界条件
1) 壁面边界处采用了无滑移条件,其中管道运输壁面附近的速度为零。

(8)
(9)
3) 出口的边界条件为“压力”,其值可在不可压缩的情况下任意设定,在可压缩结构的情况下这将影响应力,从而影响固体的变形。因此,我们将出口的参考压力设为零[28-30],并且抑制回流。
2.4 网格划分
为了实现网格的无关性,逐渐增加网格的密度,比较在管道内水流流量 50 m3/h条件下,不同网格尺寸对管道车静止于平直管道的几何模型中管道车料筒中部壁面主应力的影响,直到差异降至3%以下,从而选择出了合理的网格尺寸。
为了减少计算量和模拟时间,采用了不同的子域密度:管道水流采用5 mm的最大单元尺寸进行网格化。管道车以2 mm的最大元素尺寸进行网格化,而边界层层数设置为5,第1层网格的厚度设置为0.005 mm,网格的层间比例因子设置为1.2.最后的模型由1 752 472个元素组成,网格平均质量为0.956 4.
3 模拟结果验证
为了验证数值模拟的可靠性,通过试验研究对距管道车料筒壁面1 mm处的水流的轴向速度和管道车料筒壁面主应力分布两方面对模拟结果进行了验证。验证试验的管道水流流量为30 m3/h.由于管道车支脚的存在,管道车料筒周围流场分布和料筒壁面主应力的分布均关于Z轴对称,因此只列举了0 °~150 °的情况。
如图3所示,管道车静止在管道水流中,水流方向为从左向右。顺水流方向,定义管道车的左端为车后端(图7和图8中水平轴X距离为0 mm的位置);右端为车前端(图7和图8中水平轴X距离为150 mm的位置)。
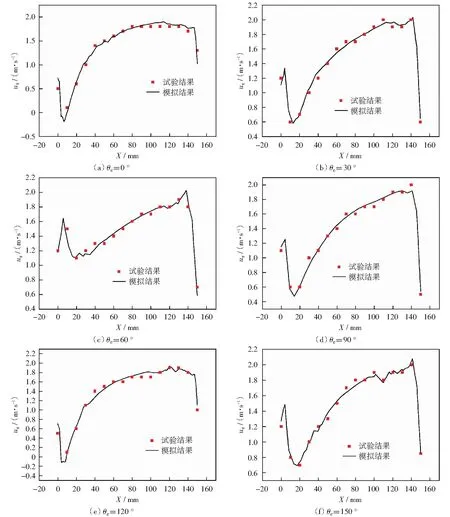
图7 轴向速度试验值和模拟值的对比Fig.7 Comparison of simulation results and experiment results for axial velocity
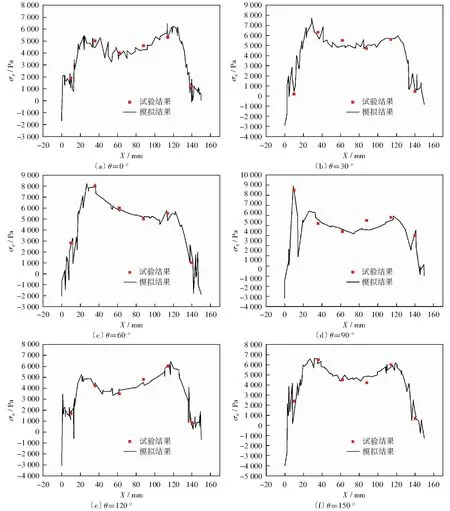
图8 主应力周向分量模拟结果和试验结果对比Fig.8 Comparison of simulation results and experiment results for circumferential component of the principal stress
3.1 轴向速度分布
图7为管道车静止于水平管流中距管道车料筒壁面1 mm处的水流轴向速度试验值和模拟值的对比结果。如图7所示,模拟结果和试验结果基本一致,最大相对误差不超过8.21%.管道车壁面附近水流的轴向速度的大小和分布情况对管道车壁面切应力大小和分布有很大的影响。
从图7中可以看出,管道车料筒壁面附近的轴向速度在料筒两端出现突然下降,其余位置沿管道车壁面逐渐增加,这主要是管道车料筒的两端过流面积的突变引起的压强变化导致的,而在远离管道车两端的中部位置由于管道车和管壁之间缝隙流的压强沿管道车壁面沿程降低引起轴向速度远程增加,这与LIU et al[2]和KHALIL et al[14]的研究结果一致。
3.2 主应力的周向分量
图8为管道车料筒壁面(0°~150°)的主应力的周向分量模拟值和试验值的对比情况。从图中可以看出,管道车壁面主应力的周向分量的模拟值和试验值基本一致,最大相对误差在9.80%以内。图8(a)和8(e)是位于管道车两个支脚之间的料筒壁面主应力的周向分量的分布情况,即θ=0 °和θ=120 °.其分布情况类似,最大值出现在料筒前部125 mm附近的位置,其值约为6 000 Pa,料筒的前端和后端的主应力的周向分量值较小,其值大约为1 000 Pa,个别位置出现负值,料筒中部的主应力周向分量稍有所下降。料筒壁面主应力的周向分量整体上呈“M”分布。除θ=90 °,其它位置的料筒壁面主应力的周向分量最大值均出现在料筒后段30 mm位置附近。最大值约为8 000 Pa,最小值同样出现在料筒的两端位置。图8(d)是θ=90 °时壁面主应力周向分量的分布情况,其最大值出现在料筒后段10 mm附近的位置,最大值约为9 000 Pa,同时也是该工况下整个料筒壁面的最大值。
4 结果与讨论
4.1 速度分布
图9为管道车不同流量时XZ平面的速度分布云图。从图中可以看出,管道车的存在使管道水流的流速分布发生很大的变化,而单相流水流的流速呈对数分布,且流线平行于管轴线[31]。在管道车的下游顺水流方向向后延伸有一个漩涡区域(常称为尾涡区),在该区域均存在对称的漩涡,且旋转方向不同。这是因为在管道车上下两表面流下来的水流在管道车的下游相遇,它们保留了展向的动量,因此在分界面的上下两侧流体具有相反的横向速度分量,也是一个切向速度的间断面,实质上也是一个涡面,涡面上的漩涡轴线方向应与速度差垂直,故该尾涡区沿水流方向有着不同的旋转方向[32]。对比不同流量时管道车周围流场的情况,可以看出随着管道水流流量的增加,管道车周围水流的流速逐渐增大,尤其是管道车与管道之间的水流流速变化很大。这主要是因为管道车与管道之间的过水面积较小,单位流量的变化引起水流流速的变化和其他区域相比要大。在管道车与管道之间的缝隙区域,流速梯度变化很大,在靠近管道车外壁和管道内壁的水流流速很小,中间位置水流的流速很大,该现象符合粘性底层的理论[33]。而且靠近管道内壁的低流速区域比管道车外壁附近的低流速区的范围要小。这是因为在管道内壁区域水流主要受流体粘性产生的摩擦阻力影响,而在管道车的外壁区域水流不仅受到摩擦阻力的影响,水流的流动分离引起的压差阻力对该区域水流的流速也有影响[34]。靠近管道车外壁和管道内壁的低流速区域随着管道水流流量的增大而减小。
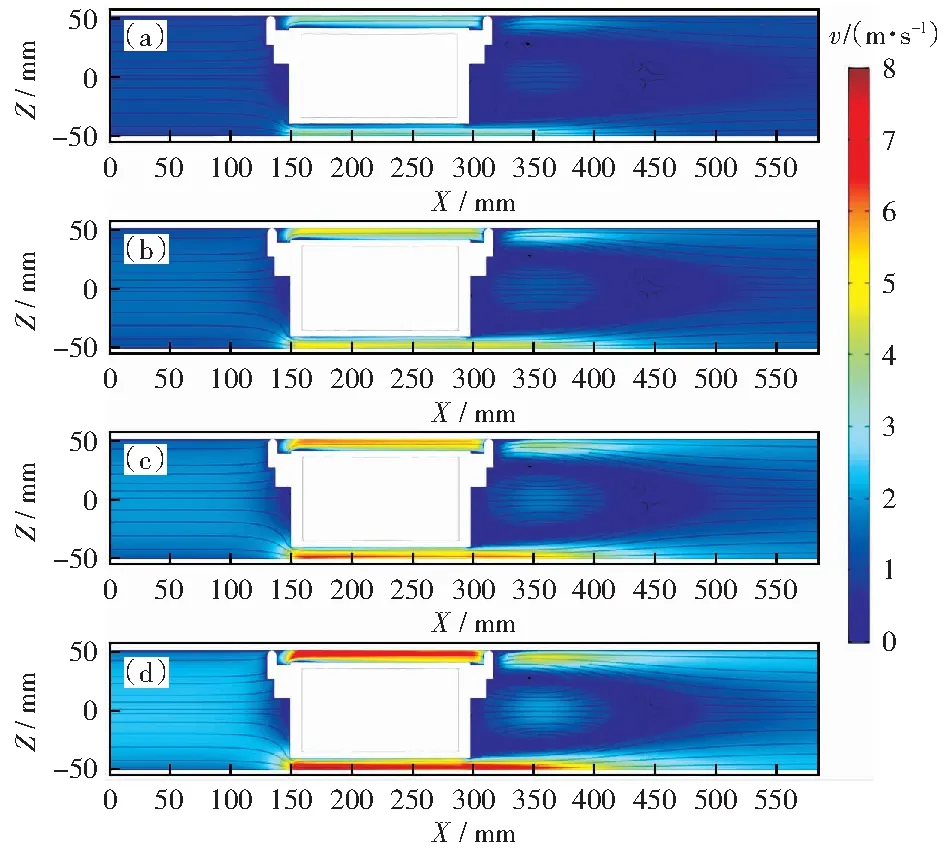
(a) Q=30 m3/h, (b) Q=40 m3/h, (c) Q=50 m3/h, (d) Q=60 m3/h图9 不同流量时XZ平面速度分布云图Fig.9 XZ planar velocity distribution clouds at different flow rate

图10 不同流量时壁面剪切应力分布图Fig.10 Wall shear stress distribution at different flow rate
4.2 壁面剪切应力分布
图10为管道车不同流量时壁面剪切应力分布图。对比不同流量管道车料筒壁面的剪切应力可以看出,管道车料筒壁面剪切应力的大小随着管道水流流量的增加而增大,这是因为管道车料筒壁面剪切应力的大小与管道内壁和管道车外壁之间缝隙流速的平方成正比。管道水流流量的增加必然引起该区域水流流速的增加,故而壁面剪切应力增大。管道车料筒壁面剪切应力均大于零,说明壁面剪切应力沿管道水流的方向。从图中还可以看出,管道车料筒壁面的剪切应力关于Z轴对称,剪切应力的最大值出现在料筒中后段,且位于两组支脚之间,如0 °和120 °之间。而在前后一组支脚之间的壁面剪切应力较小。这主要受管道车支脚的影响,如图9所示,前后一组支脚之间的水流流速较环状缝隙其它位置水流的流速小。
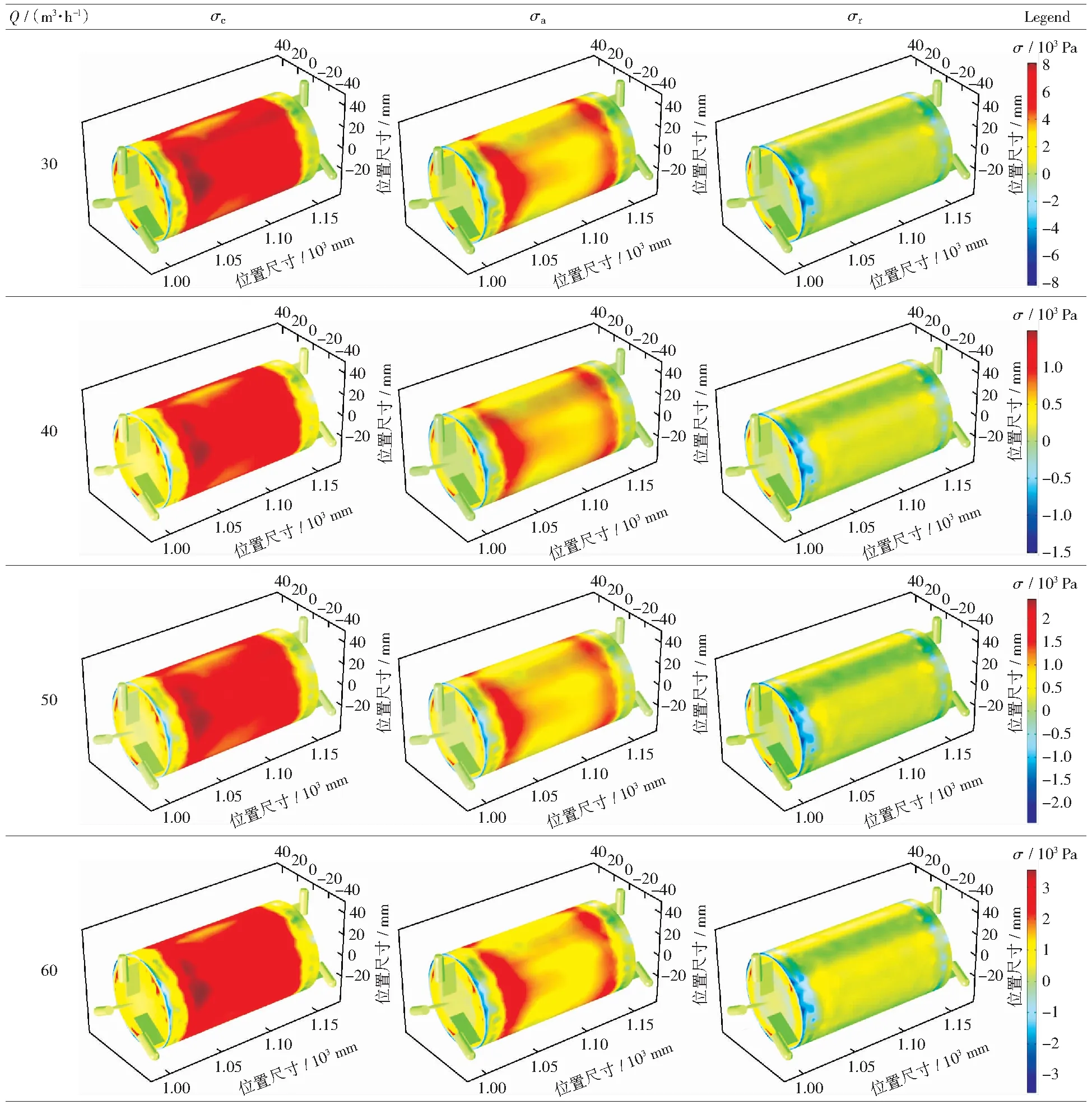
图11 不同流量时壁面主应力分布图Fig.11 Distribution of wall principal stress at different flow rate
4.3 壁面主应力分布
管道车壁面主应力分为管道车轴线方向平行的轴向分量σa,与管道轴线方向垂直的沿料筒的周向分量σc,以及沿半径方向的径向分量σr.且主应力的周向分量>主应力的轴向分量>主应力的径向分量。
图11为管道车不同流量时壁面主应力分布图。从图中可以看出,随着管道水流流量的增加,管道车料筒壁面主应力的三个分量均增大,流量对主应力的三个分量的影响情况,在4.4节做详细介绍。主应力周向分量和轴向分量的分布情况类似,从管道车的后端到前端依次为先增大后减小再增大再减小的“M”型分布,最小值出现在管道车的最后端和最前端,且为负值;两个最大峰值分别出现在距料筒前端和后端均为25 mm的位置附近,而且在距料筒后端25 mm附近两组支脚之间出现最大值。这主要是因为水流经过管道车后端时引起流动的分离产生逆压区,在该区域水流方向发生变化,从而使得主应力周向和轴向分量出现负值。流场在管道车后端分离后,压力很快降低,这时从壁面分离后的流体又会重新附着在壁面上,当流体快到达管道车前端时,运动的流体既要克服管道车料筒外壁的粘性作用,又要抵抗过水端面突然扩大引起的压差,以至于流动再次分离,当部分流体质点不足以克服这两者的作用时,将再次出现逆压区产生回流,主应力周向和轴向分量再次出现负值。管道车料筒壁面主应力的径向分量和主应力的其他两个分量相比很小,最小值同样也是出现在料筒前端和后端的位置。
4.4 流量对管道车料筒壁面应力的影响
这里以θ=0 °时料筒中间位置为例来讨论流量分别对管道车料筒壁面切应力和主应力三个分量的影响情况,如图12所示。用变量k表示单位流量对管道车料筒壁面应力的影响大小。
(10)
式中:ΔM表示管道车料筒壁面的应力差值,ΔM=M1-M2,Pa;ΔQ表示流量差值,ΔQ=Q1-Q2,m3/h.
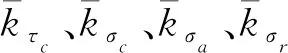

图12 管道车料筒壁面各应力随流量的变化Fig.12 Variation of stress on the cylinder wall of piped carriage with flow rate

表2 管道车车身壁面各应力单位流量的变化率Table 2 Rate of unit flow of stresses on the cylinder of piped carriage
5 结论
管道车水力输送过程中,水流作用在管道车料筒壁面的应力对料筒材料的选择有重要的工程意义。本文通过数值模拟的方法探究了管道车静止于不同流量管流中时周围流场的分布和管道车料筒壁面应力的分布情况,并通过模型试验验证了模拟结果的可靠性,得出以下结论:
1) 随着管道水流的流量的增加,管道车周围水流速度明显增大,尤其是管道内壁和管道车之间区域。
2) 管道车料筒壁面剪切应力均大于零,即壁面剪切应力沿管道水流的方向,且最大值出现在料筒中后段的两组支脚之间。
3) 在该试验的四种流量工况下,管道车料筒壁面主应力的周向分量σc的最大值为35 653,主应力的轴向分量σa的最大值为33 144,主应力的径向分量σr的最大值为32 470.且从管道车的后端到前端依次为先增大后减小再增大再减小的“M”型分布,最小值出现在管道车的最后端和最前端,且为负值;在距料筒后端25 mm附近两组支脚之间出现最大值。