基于跟踪微分器的姿控喷管故障检测

张 凯，杨小龙，杨宇和

(北京宇航系统工程研究所，北京 100076)

0 引 言

航天飞行器包括卫星、运载火箭、弹道导弹等，具有重要的经济价值或战略价值，其设计要求具有极高的可靠性，具有容错控制能力的姿控系统是高可靠性的重要保障，因此对于航天飞行器姿控系统的故障诊断便成为必要[1-2]。故障诊断方法包括基于模型的故障诊断、基于信号的故障诊断和基于知识的故障诊断[3-4]。

现有的关于航天飞行器姿控喷管故障诊断国内外文献较少，国内相关文献多集中于伺服机构的故障检测、诊断[5-7]。张亚婷等[8]提出了姿控喷管的故障诊断方法，即通过设计观测器，对比观测器输出信号和真实信号的残差，从而判定故障是否发生，属于基于模型的故障诊断。该方法的关键是故障发生时残差信号阈值确定[9]，通过大量仿真归纳给出阈值的确定方法，尚不具备普适性。

根据文献[10]，观测器方案对于初始的故障不敏感，故障检测有较长延时。本文采用跟踪微分器来估计姿控喷管实际输出力矩，通过与指令力矩的对比来检测故障。微分器应用于故障检测领域的文献较少，文献[11-12]研究了基于微分器的传感器故障检测，文献[13]设计了自适应增益的微分器，并应用于飞机舵面震荡的故障诊断。本文从理论上推导了估计力矩的变化范围，设计了根据指令和角速度等变量自适应变化的估计力矩变化包络，解决了阈值选取问题，并且通过仿真验证了所提方法的有效性。

1 研究模型及姿控喷管布局

研究对象为一假设的航天飞行器模型(模型参数为非真实参数，但不影响其对本文所提出方法验证的可参考性)，研究目的在于识别其空间飞行段的姿控喷管故障。其姿控喷管布局尾部视图如图1所示。该模型为刚体，不考虑柔性。P1～P6为姿控喷管，单个喷管推力为100N，P1，P6，P3，P4控制俯仰；P1，P4，P3和P6控制滚转；P2，P5控制偏航。相关姿控动力系统性能参数如表1所示。

图1 模型喷管布局

喷管推力用为一阶环节加延时环节模拟，表示如式(1)，其中延时环节的延时时间和一阶环节的时间常数满足热启动加速性和热关闭减速性的要求。

(1)

2 跟踪微分器设计

由于实际的执行机构存在安装偏差、推力大小偏差、延时等不确定因素，姿控喷管的输出与指令期望的输出会有一定的误差。姿控喷管正常工作时，误差会在一定“限度”内，当姿控喷管出现故障时，姿控喷管输出与指令期望输出会有较大不一致，误差超过这个“限度”。因此如果能估计出姿控喷管的输出并与指令期望的输出做比较，并寻找到合适的“限度”，便可以通过判断误差是否在“限度”之内来确定姿控喷管是否出现故障。

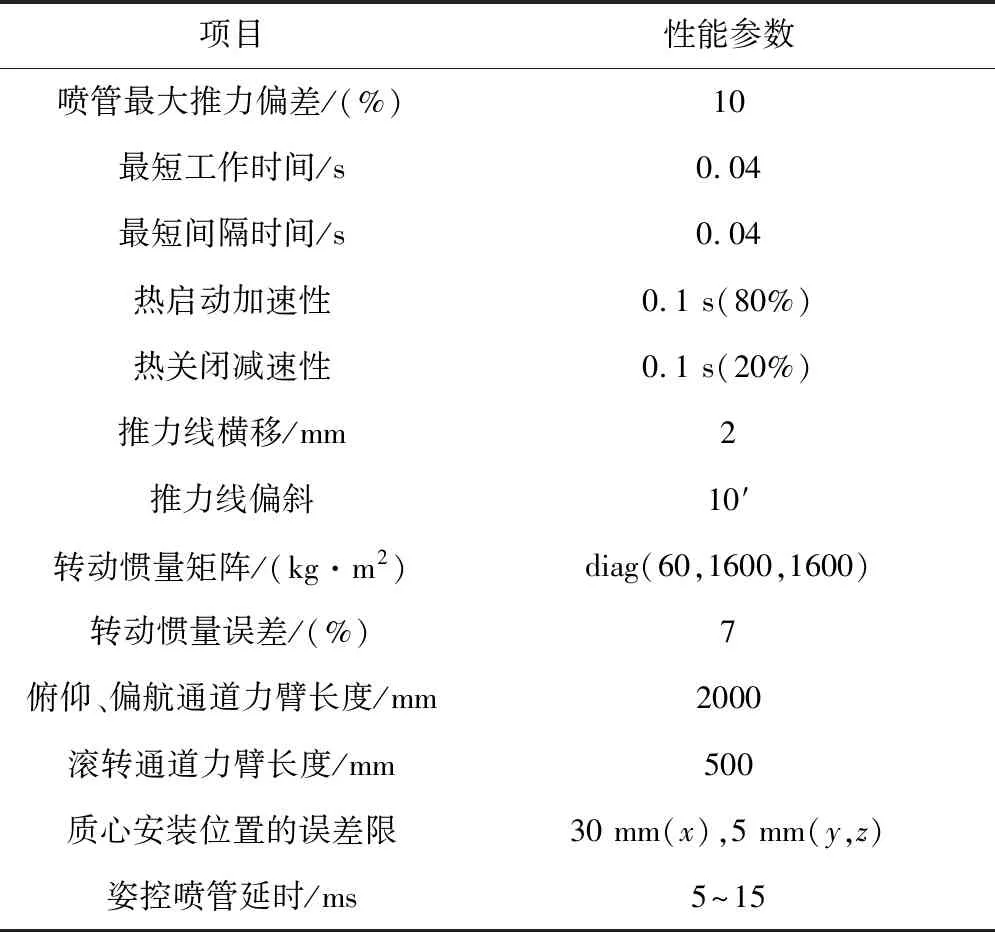
表1 姿控动力性能参数

对于本文中所讨论的航天飞行器的姿态运动，其角速度可测，可以利用跟踪微分器跟踪角速度来得到角加速度，进而得到喷管实际的输出，因此构造跟踪微分器是本方法的基础。

考虑航天飞行器的姿态运动，可视其为刚体，其动力学方程如下

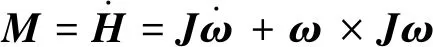
(2)

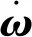
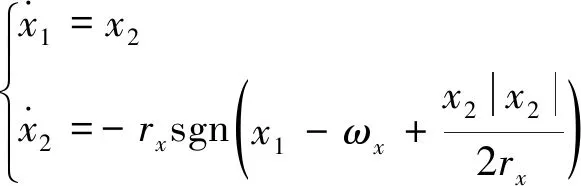
(3)

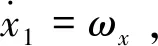
实际使用的跟踪微分器为其离散形式，离散系统中从非零初值到达原点的最速控制综合函数记为

u=fhan(x1,x2,r,h)

(4)

展开如下[14]，h为离散步长

(5)

其中，

fsg(x,d)=(sgn(x+d)-sgn(x-d))/2

(6)

以x轴为例，用x1-ωx替代x1，则得到离散化的跟踪微分器

(7)

如果输入信号被噪声污染，那么跟踪微分器输出的微分信号将会放大噪声，但是如果将fh=fhan(x1,x2,r,h)中的h改为与步长独立的新变量h0，将其取为适当大于步长的参数，就可以抑制微分器对噪声的放大。

与原微分信号相比，理想的跟踪微分器输出的微分信号应该延时小且噪声小，为减小延时，应该增大r且减小h0，但这会放大噪声；为减小噪声则需要执行相反的操作从而使延时增大。综合考虑延时和噪声的影响选取合适的r值和h0值也是不可行的，因为跟踪微分器跟踪较大的微分信号时会有比较大的延时，跟踪小的微分信号时会有比较小的延时，在抑制噪声的前提下难以选取合适的r和h0来减小跟踪大微分信号的延时，并且这种不一致的延时难以补偿。

为保证噪声较小且延时可补偿，本文采用串联低通滤波器。首先选取合适的h0和比较大的r值，此时跟踪微分器输出的信号噪声很大,但对于大的微分信号和小的微分信号的延时都很小,所以可以忽略两种延时的不一致；然后将这一信号通过低通滤波器，获得滤除噪声后的微分信号,低通滤波器会使信号产生一个一致的延时,跟踪微分器的延时远小于滤波器的延时，因此可以忽略微分器的延时，只补偿低通滤波器的延时就可以达到延时补偿的目的，延时的具体补偿方法见第3.3节。

低通滤波器的设计可以采用一阶环节或二阶环节等。由文献[13]可知，小时间常数的一阶环节可近似为延时环节，有

(8)

由模型参数可知，姿控喷管最短工作时间为0.04 s，因此角加速度增大、减小的最短周期为0.08 s，因此如果带宽达到1/0.08·2π≈78.5便可以达到要求，实际的带宽选择可参考此值并根据噪声的特性来考虑，如果低通滤波器为二阶环节，可将其等效为两个串联的一阶环节，并根据式(8)计算低通滤波器造成的延时。

3 控制力矩包络分析

根据得到的微分信号可以解出飞行器所受的力矩，该辨识力矩与指令力矩的误差由两部分构成：实际力矩与指令力矩的偏差，辨识力矩与实际力矩的偏差。前者的主要构成是姿控喷管推力偏差、姿控喷管安装误差、质心误差，后者的主要构成是转动惯量偏差、跟踪微分器输出信号的偏差。指令力矩加上这两种误差和的上限便是上包络，指令力矩加上这两种误差和的下限便是下包络，若辨识力矩处于上下包络内便可认为其工作正常，反之则发生了故障。

3.1 实际力矩与指令力矩的偏差

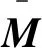
(9)

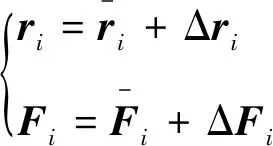
(10)

式(9)化简到最后右边有3项，第3项属于高阶小量，可以直接略去；对于第1项中的ΔFi，包括了推力线的偏斜导致的方向变化和推力不稳定导致的推力大小变化，然而推力线偏斜仅仅有10′，tan(10′)<0.003，可以忽略，因此只考虑推力大小变化；对于第2项，推力线偏移只有2 mm，但是考虑ri为飞行器质心到喷管中心线上的垂点的矢径，因此质心的变化也会影响Δri，故将Δri拆解为2部分如下

(11)

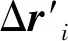
(12)

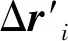
由于每时每刻的喷管的开关状态都不一样，所以式(12)要添加喷管指令的开关信息

(13)

其中，sw(i)为第i个喷管的开关函数，其值取1或者0，1表示喷管开，0表示喷管关。令Δrxm，Δrym，Δrzm分别为Δrc在3个方向上的误差限，皆为正数，即有

(14)

将式(13)等号右边第二项展开，考虑到Δrc的分量都为正，得到

(15)

式中：sw(i)可以通过控制器指令得到，除此之外其他所有量都已知。将式(13)等号右边第一项展开可得

(16)

式中：sw(i)可以通过控制器指令得到，除此之外其他所有量都已知。因此实际力矩与指令力矩的偏差的上限可以由式(15)和式(16)确定。

3.2 辨识力矩与实际力矩的偏差

根据跟踪微分器得到的角加速度和已知的标称转动惯量，可以计算飞行器所受力矩，辨识的力矩表示为

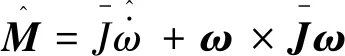
(17)

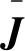
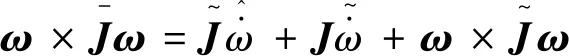
(18)

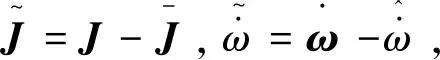
(19)

可整理得到误差力矩的上限如式(20)

(20)

(21)

由此可知辨识力矩与实际力矩的偏差主要由转动惯量偏差和跟踪微分器输出信号的误差两部分构成，其中转动惯量造成的偏差又由两部分构成：角加速度引起的辨识误差和角速度耦合引起的辨识误差。

3.3 包络线的确定

(22)

下限为

(23)

其中实际力矩与指令力矩的偏差由推力大小偏差和质心位置偏差构成，二者表达式见式(15)和(16)，其表达式包含sw(i)即姿控喷管的开关函数，意味着这两项偏差只在姿控喷管开启时起作用，而姿控喷管的性能有一个上下限，即从下达姿控喷管指令开始到姿控喷管输出到达均匀，其整个过程的“时间-推力”曲线可以由两条姿控喷管性能包络曲线来框定，上下包络表示姿控喷管正常工作时输出推力的最大值和最小值。

对单个喷管而言，当喷管开启时，其上包络线为喷管最大推力值经过一阶环节和延时环节得到的曲线，其中延时环节的延时和一阶环节的时间常数都要小于喷管的最好性能对应的数值；当喷管关闭时其上包络线为0经过一阶环节和延时环节得到的曲线，其中延时环节的延时和一阶环节的时间常数都要大于喷管的最差性能对应的数值，其特点总结为：推力大，升的快，降的慢。

当喷管开启时，其下包络线为喷管最小推力值经过一阶环节和延时环节得到的曲线，其中延时环节的延时和一阶环节的时间常数都要大于喷管的最差性能对应的数值；当喷管关闭时其下包络线为0经过一阶环节和延时环节得到的曲线，其中延时环节的延时和一阶环节的时间常数都要小于喷管的最好性能对应的数值，其特点总结为：推力小，升的慢，降的快。

因此确定力矩包络时，对于所有由喷管引起的力矩偏差都要通过上下包络线的延时和一阶环节再叠加到指令力矩，而不是简单加减。

因为在推导过程中略去了一些小量，因此在真实的包络线确定过程中可以在各个通道叠加一个常值力矩作为补偿。

当包络确定后如果辨识的力矩曲线越过了包络线并持续了一段时间tconti便可认为喷管发生了故障。tconti的取值要综合考虑误检率和漏检率,由于存在噪声,喷管无故障时辨识力矩可能短时间超过力矩包络,故tconti太小会造成误检;故障与指令冲突时该故障才能暴露,若某故障暴露时间短则辨识力矩超过包络的时间就短,因此tconti太大会造成漏检。

4 仿真校验

通过仿真验证所提方法的有效性，包括跟踪微分器的有效性，姿控喷管正常工作情况下的误检概率以及姿控喷管故障时是否能迅速检测出故障。

仿真中跟踪微分器参数为h0=0.005 s，rx=3333，ry=250，rz=500；低通滤波器为

(24)

(25)

喷管启动(关闭)时下(下)包络的传递函数环节

(26)

4.1 跟踪微分器

仿真初始姿态为[0°,0°,0°]，目标姿态为[50°,50°,50°]，控制器为采用极限环方法，各通道独立控制。以x轴为例，仿真如图2所示。

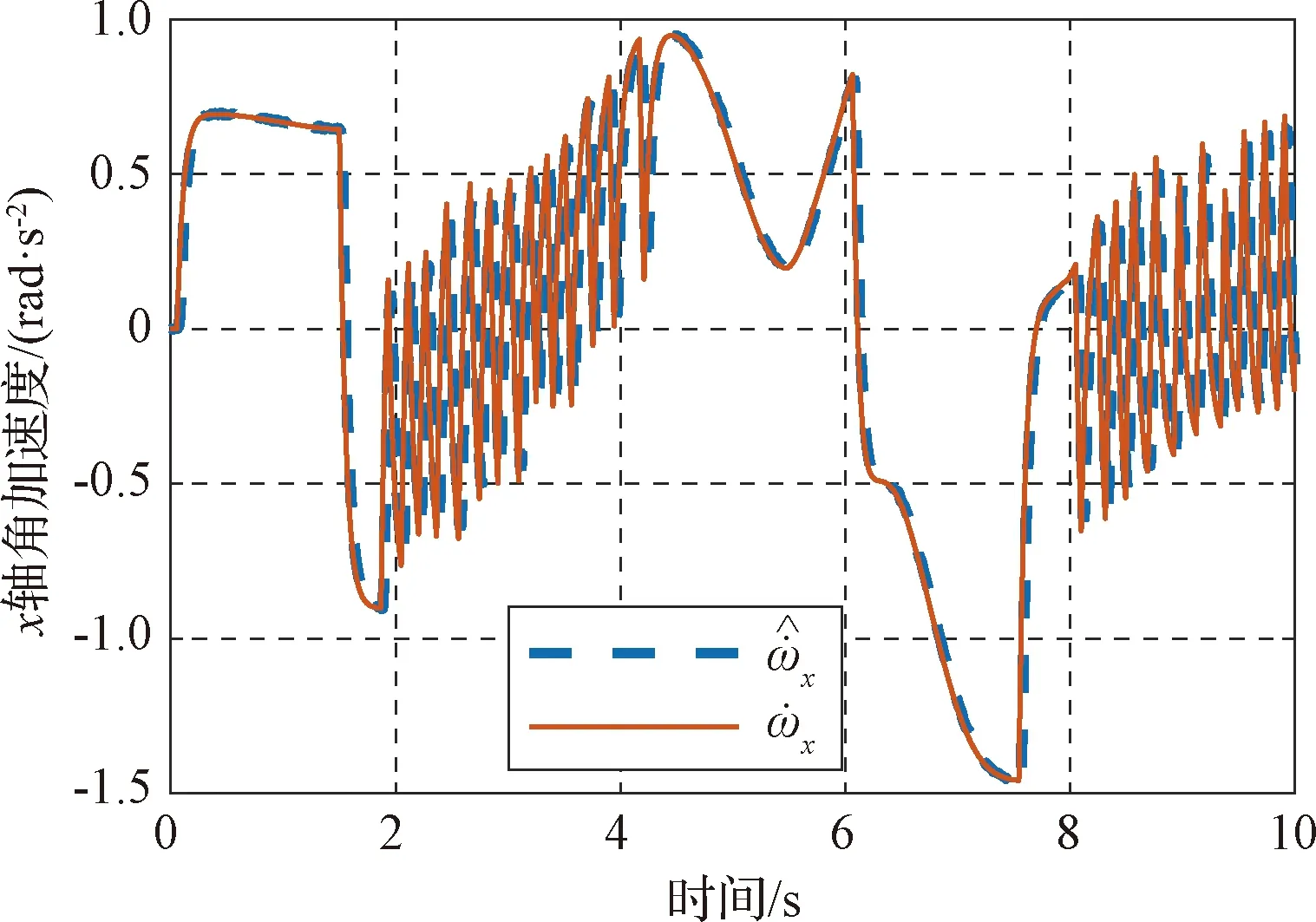
图2 跟踪微分器仿真效果

图2表示跟踪微分器跟踪轴x的角加速度曲线，可见跟踪微分器的性能良好。

4.2 无故障情形

由前文的力矩偏差分析可知，辨识力矩与指令力矩误差的主要原因为喷管推力大小误差、质心偏移、转动惯量误差、角速度耦合、角加速度辨识误差，其中前三个原因需要通过硬件改良，角加速度辨识误差的减小需要良好的跟踪微分器，角速度耦合可以在姿态机动过程中极大程度避免，比如姿态机动时各个轴依次机动而非同时机动，因此在这一部分中进行了两组仿真，第一组耦合比较严重，模拟极限情况，第二组为耦合不严重，模拟正常情况。

两组仿真中各个有误差的参数均取其极限值，比如推力标称值100 N，偏差为10%，则仿真中姿控喷管推力为110 N或90 N。这些取极限的参数包括推力大小、推力线横移、推力线偏斜、转动惯量、实际质心与理论质心距离的误差。

对第一组仿真，仿真初始姿态为[0°,0°,0°]，目标姿态为[50°,50°,50°]，控制器为采用极限环方法，各通道独立控制，在三轴均大角度机动时姿态会发散，各通道角速度耦合严重，验证在此极端情况下的包络选取的合理性。该组仿真共进行了2552次，每次仿真10 s。其中有81次辨识的力矩曲线越过了包络线，但其中越过包络线时间最长的一次也仅仅持续了0.004 s，此值远小于tconti=0.02 s，因此可认为此情况下误检率为0。图3给出该组仿真中某次仿真的曲线。

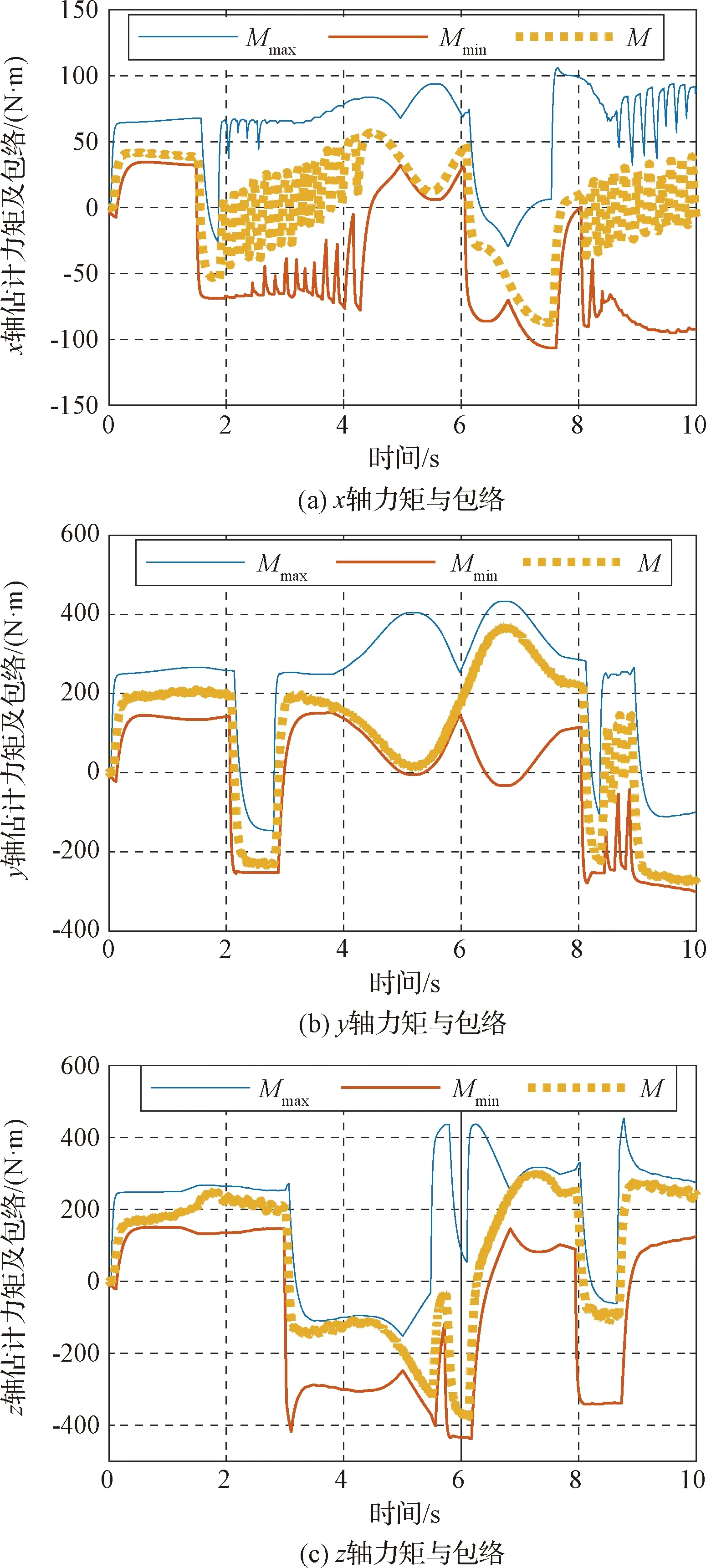
图3 无故障检测(严重耦合)

对第二组仿真，初始姿态[0°,0°,0°]，目标姿态[10°,10°,10°]，其余条件与第一组相同。该组仿真共进行了884次，每次仿真10s。其中有0次辨识的力矩曲线越过了包络线，因此可认为此情况下误检率为0。图4给出该组仿真中某次仿真的曲线。

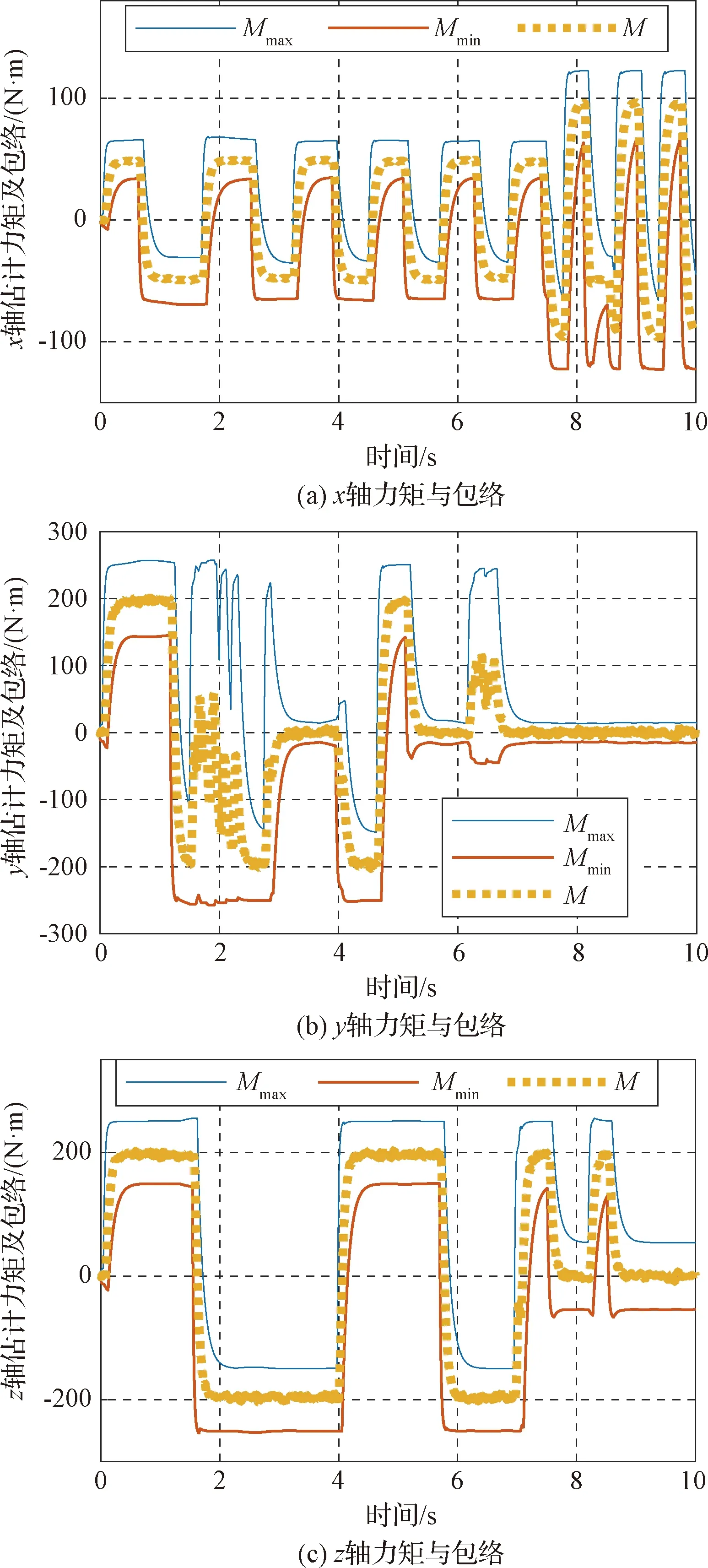
图4 无故障检测(一般耦合)

4.3 有故障情形

姿控喷管故障包括喷管常开、喷管常关与喷管极性接错3种。本组仿真初始姿态为[0°,0°,0°]，目标姿态为[10°,10°,10°]，控制器与无故障情形相同。每次仿真时长10 s，第5 s时加入故障，假设3种故障发生概率相同。需注意当故障与指令发生冲突时故障才能凸显，例如发生P1喷管常开的故障，若指令一直让P1输出推力，则无法检测P1的故障；同理若发生喷管常关故障，只有当指令让该喷管输出推力时故障才凸显；若发生极性接错故障则当两个喷管中的一个接收到打开指令、一个接收到关闭指令时故障才凸显。

因此仿真中以5 s后指令第一次与喷管故障冲突作为故障发生的时刻，以辨识力矩曲线超过包络并持续tconti=0.02 s作为故障检出时刻，故障检出时刻减去故障发生时刻为故障检测所用时间。

本组仿真共进行675次，有24次未能检测出故障。其中12次因为故障与指令未发生冲突，故障未能凸显；另外12次因为与故障冲突的指令从5 s持续到5.015 s，持续时间仅15 ms，故障未充分暴露，因此未检测出。检出故障的651次仿真中大部分情况下可在0.1 s内检出故障，检测用时最短0.0595 s，最长3.1595 s，这是因为第一次指令与故障冲突时持续时间较短，故障未能充分暴露，因此在后面的指令、故障冲突中才检出故障，故而计时较长。

图5给出某次故障检出的仿真。

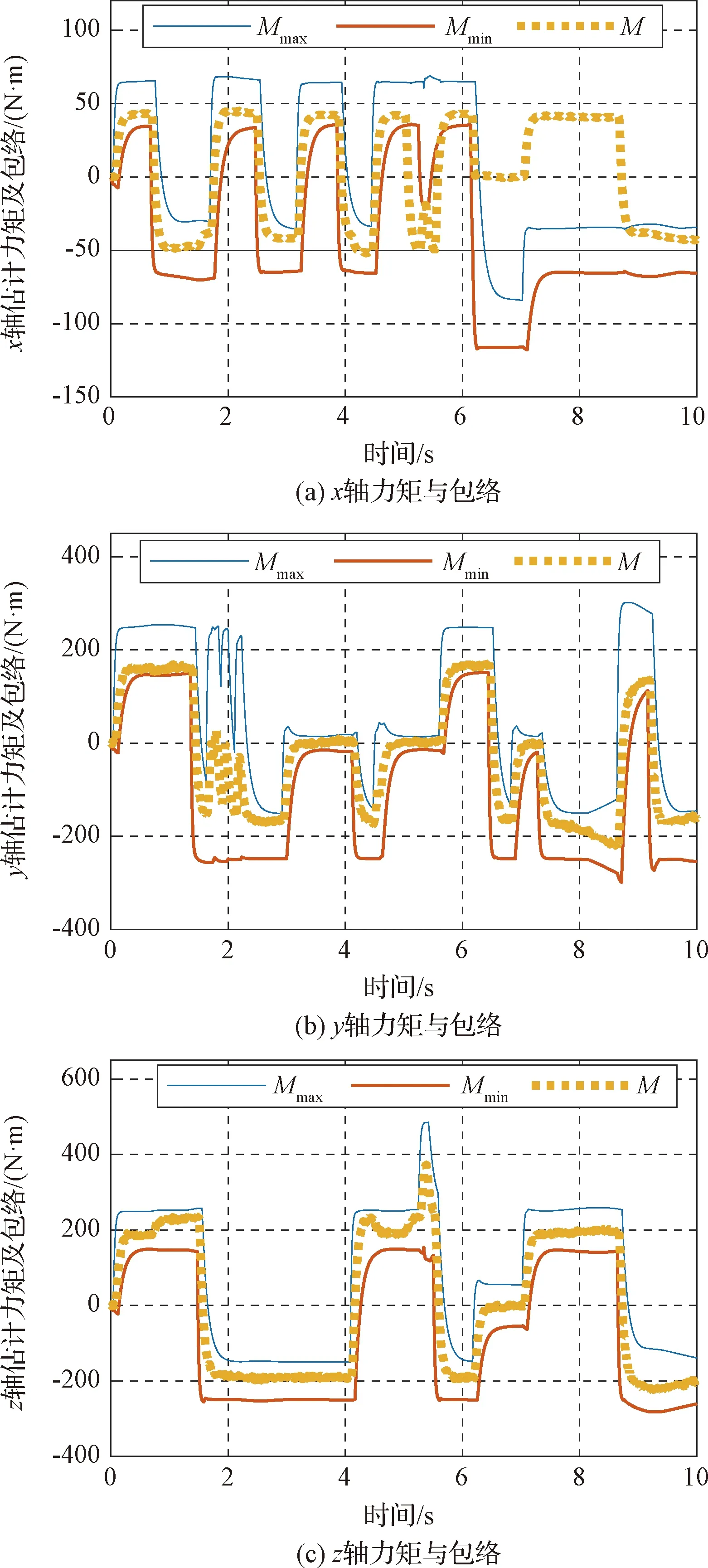
图5 有故障检测

其中此次故障为P3，P4喷管极性接错，指令与故障发生冲突时刻为5.0005 s，故障检出时刻为5.0615 s，检测用时为0.061 s。

5 结 论

本文提出了一种航天飞行器姿控喷管的故障检测方法，只需要得到角速度测量信号与姿控喷管指令信号便可以根据本文提供的方法进行姿控喷管的故障检测，这两种信号容易测量得到。本文中提到的包络设计方法需要得到喷管推力偏差、转动惯量偏差、喷管安装误差等参数，这些也可以得到。仿真表明：该方法误检率几乎为零且故障检出率高，可靠性强，并且检测时间短，具有一定的实用价值。