推力作用下变质量柔性自旋飞行器稳定性分析

潘成龙，荣吉利，徐天富，项大林

(1. 北京理工大学宇航学院，北京 100081；2. 兵器工业集团航空弹药研究院，哈尔滨 150030；3. 北京宇航系统工程研究所，北京 100076)

0 引 言

大长径比和高推重比自旋飞行器弹性效应明显，耦合问题突出，推力稳定性问题备受关注。文献[1]采用梁结构振动理论建立柔性弹箭运动模型，分析了推力作用对系统振动频率和系统稳定性的影响。文献[2-4]采用Timoshenko梁为模型，考虑陀螺效应和剪切效应，分析了随动推力作用下柔性自旋飞行器稳定性问题。文献[5]研究了变推力作用下系统质量偏心因素对自旋飞行器系统动力特性的影响。文献[6]采用变质量系统的方法，分析了旋转固体火箭发动机工作过程中的章动不稳定性问题。除此之外，飞行器在飞行时是一个典型的时变系统，燃料消耗引起变质量效应，对飞行过程有很大影响，其振动规律不同于恒定质量系统[7]。文献[8]以Kane运动方程为基础，建立考虑时变质量和几何刚度的柔性火箭结构动力学方程。文献[9]运用拉格朗日方程建立时变质量柔性火箭动力学方程，同时考虑了推进剂质量减少而导致质心移动的复杂情况。文献[10-11]采用改进欧拉中点辛差分格式、模态叠加方法和自适应Newmark法，研究变质量系统动态的动态响应，证明了自适应Newmark法对时变系统的适应性。

本文在国家自然科学基金项目“自旋飞行器横向振动的动力学与控制机理研究”工作基础上，以Timoshenko梁为模型，考虑陀螺效应和剪切效应，基于有限元法和稳定模态基底法[12]建立变质量系统振动方程，分析质量变化、推力作用和自旋转速对飞行器稳定性的影响，采用自适应Newmark法求解系统的振动响应。

1 动力学方程

1.1 动能、势能和外力功

图1 弹体模型图

如图1所示，建立准弹体坐标系Oxyz和随体坐标系O′ξηζ，忽略轴向变形，系统的动能为[3]：

(1)

式中：uy，uz分别为梁截面y向，z向的横向位移，θy，θz分别为该截面的转角，Ω为自旋转速，A为截面面积，ρ为轴段微元质量密度，I为轴段微元截面的惯性矩，lb为梁长。

考虑剪切影响，系统的弹性势能为[3]：

(2)

式中：EI为弯曲刚度，κGA为剪切刚度，上标符号“′”表示变量对x的偏导数。

随动推力做的功[3]：

(3)

轴向力PN：

(4)

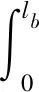
在尾部，随动推力非保守部分做的虚功[3]：

δWP=Pθz(0,t)δuy(0,t)-Pθy(0,t)δuz(0,t)

(5)

1.2 振动方程

用有限元方法，将弹体模型沿轴向进行离散，划分为n个梁单元。采用Timoshenko梁单元对横向位移和转角插值，即：

(6)

由于燃料消耗，质量随时间变化，Φ和Ψ与时间有关。采用文献[12]中提出的稳定模态基底法：

(7)

将式(7)代入式(6)中：

(8)

式中：η1(t)=B(t)q1(t)，η2(t)=B(t)q2(t)。

非保守系统Lagrange拉格朗日方程的一般形式如下：

(9)

式中：η和Q分别为广义坐标和包括非保守力在内的广义力。取η分别为η1和η2,由此得到单元的振动方程：

(10)

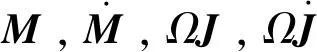
K=K1-KPN1-KP1

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

2 数值仿真及结果分析

以长径比为25.3的等截面细长回转梁模型作为仿真模型，整体分为5段，推力作用在轴段1的左端，初始时刻相关参数见表1。图2和3分别给出主动段初至末时刻单位长度质量及0～3 s燃料消耗。

表1回转梁模型参数

图2 单位长度质量

图3 主动段飞行器质量

将式(10)简化为：

(19)

将式(19)写成状态方程形式：

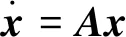
(20)

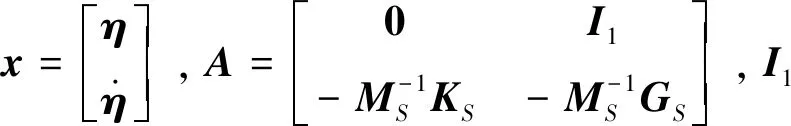
2.1 频率分析

由图4知，随着质量的消耗，系统的固有频率逐渐升高；与无推力时相比，推力能够降低系统固有频率。

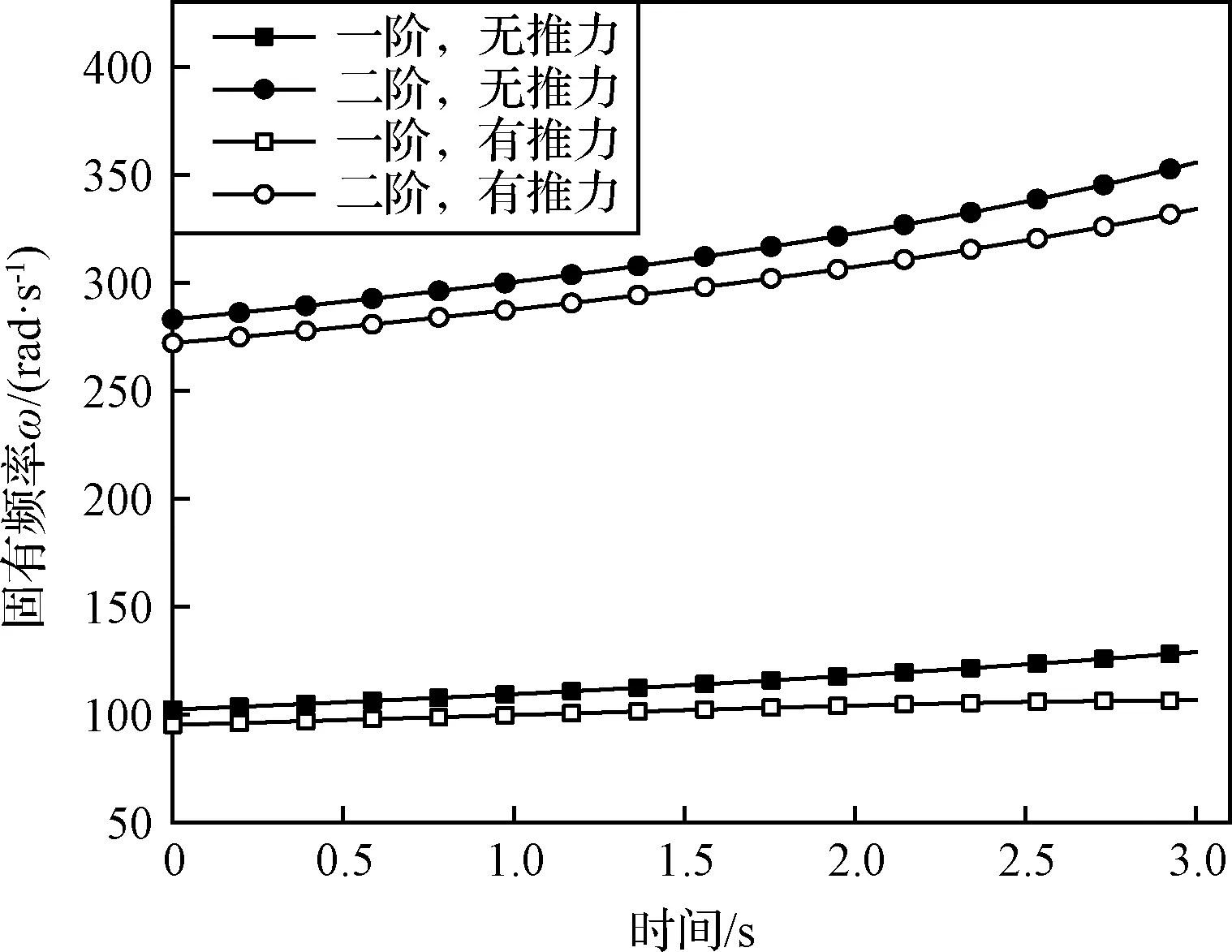
图4 固有频率变化

图5 不同推力作用下进动频率的变化

图5分析了质量和恒定推力对进动频率的影响。取恒定推力P=3.2×106N，Ω=102 rad·s-1，推力使正进动频率减少，负反进动频率减少，随着质量消耗，一阶和二阶正进动频率和负反进动频率都升高。在恒定推力和质量变化共同作用下，一阶进动频率变化斜率越来越小，在t>2.5 s，接近零，进动频率趋于不变。

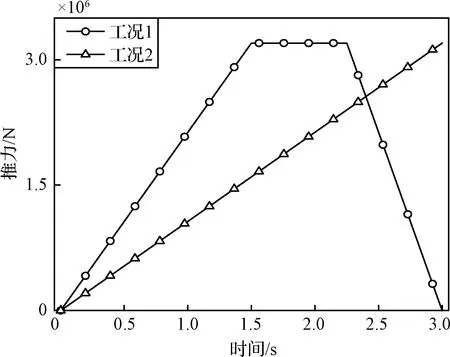
图6 推力变化

图7 不同工况下进动频率变化

图7分析了质量和变推力对进动频率的影响，推力变化如图6所示。取Ω=102 rad·s-1，由图7(a)知，工况1推力增大时，一阶正进动频率和负反进动频率先增大后减小，整体呈增大趋势，说明这段时间质量消耗对进动频率影响大于推力作用，工况2在推力增大段，一阶正进动频率和负反进动频率先增大后减小，整体呈减小趋势，推力作用更明显；工况1推力不变和减小时，一阶正进动频率和负反进动频率逐渐正增大，推力减小时，进动频率变化斜率要大于推力不变时。由图7(b)知，二阶正进动频率和负反进动频率逐渐增加，进动频率变化斜率受推力变化影响。

图8分析了质量和推力对临界转速ωcr的影响，ωcr采用文献[14]中方法计算得到。无推力时，随着质量消耗，临界转速逐渐增大；恒定推力作用时，临界转速变小，临界转速变化斜率越来越小，在t>2.5 s，接近零，临界转速率趋于不变；工况1和2推力增大时，临界转速先增大后减小，工况1推力不变和减小时，临界转速逐渐增大。

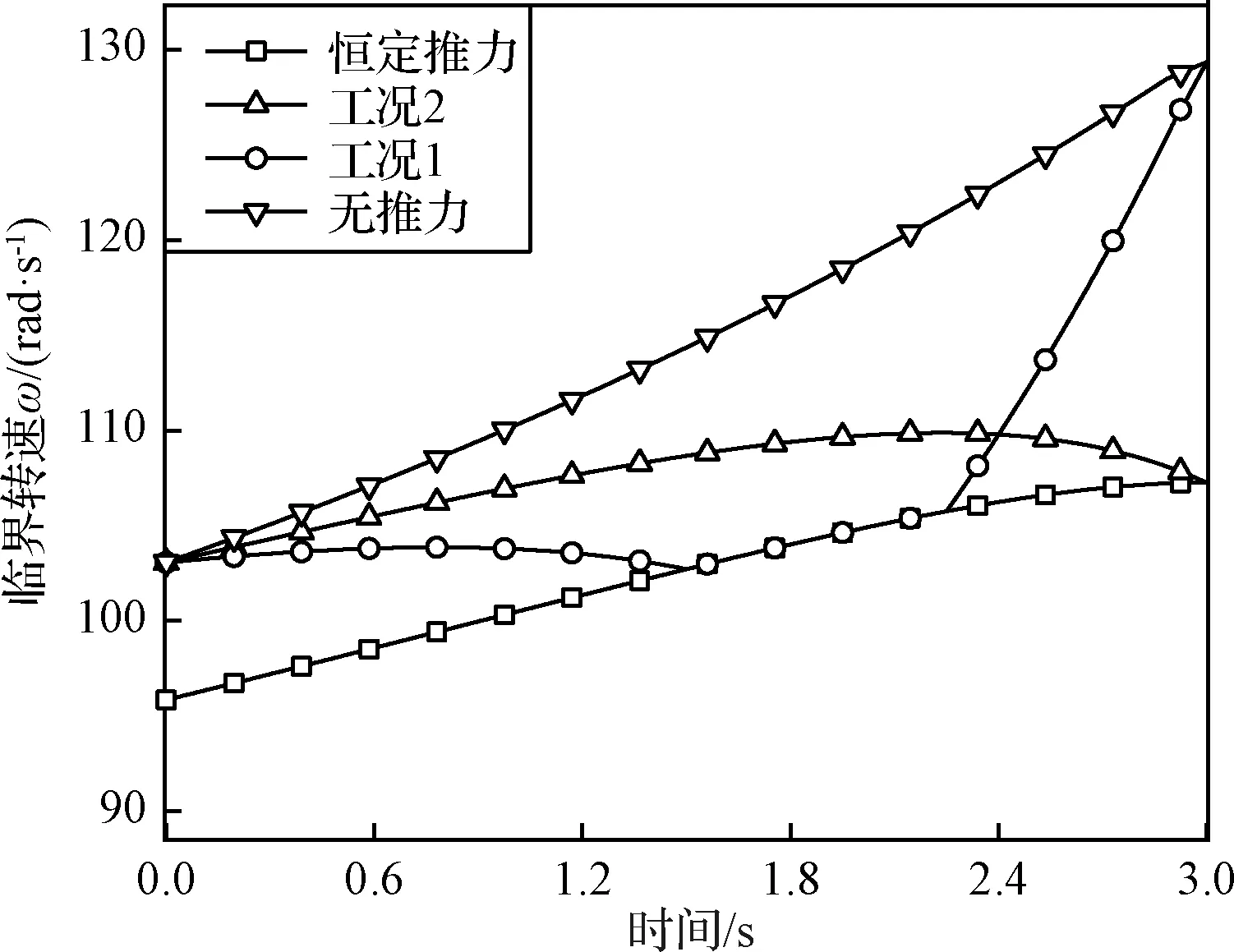
图8 临界转速

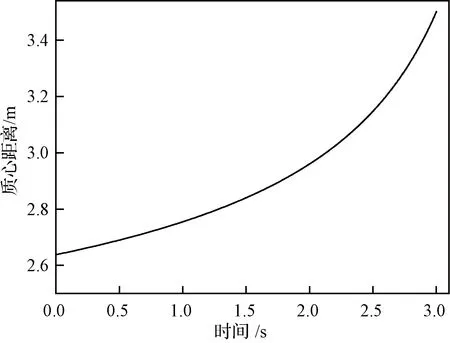
图9 质心位置

图9中，初时刻，质心到尾部的距离为2.64 m，随着质量减少，质心向头部移动，移动速度变大，末时刻，到尾部的距离变为3.5 m。

2.2 振动响应分析

经典Newmark法的迭代计算公式为：

(21)

(22)

在时变系统的振动问题中，参数随时间变化，采用自适应Newmark法[10]进行求解，步长h和β为：

(23)

(24)

(25)

(26)

式中：h(t)为自适应步长;κ为步长控制因子；ω(t)为最高阶振动角频率；ξ为系统模态阻尼比。

采用自适应Newmark法分析由激振力引起的变质量系统横向振动响应问题，激振力作用于飞行器尾部y,z向，大小均为2000 N，激振频率与自旋转速相同。

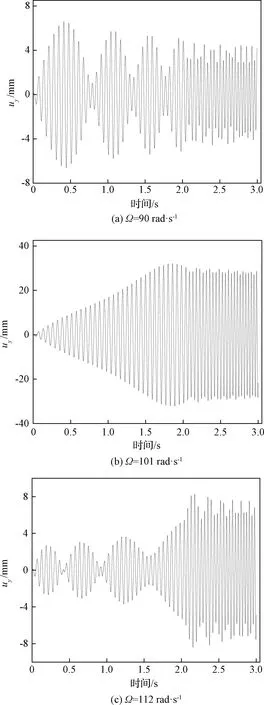
图10 不同转速下尾部位移响应

分别计算自旋转速Ω为90 rad·s-1,101 rad·s-1,112 rad·s-1时横向位移响应情况。由图8知，恒定推力P=3.2×106N时，ωcr在初和末时刻分别为95.8 rad·s-1和107.2 rad·s-1。图10(a)中自旋转速小于ωcr，受质量消耗影响，尾部振幅减少；图10(b)中振幅逐渐增大，在1.8 s时振幅达到最大，后逐渐减小，由图8可知，在1.1 s时，自旋转速等于临界转速，系统发生短暂共振,共振响应峰值最大时刻与自旋转速和临界转速重合时刻相比延迟0.7 s；图10(c)中质量消耗，临界转速增加，趋向于自旋转速，导致尾部振幅逐渐增加。

3 结 论

以柔性自旋飞行器为研究对象，采用变质量Timoshenko梁为模型，基于有限元法和稳定模态基底法建立时变系统横向振动方程，通过算例仿真，分析变质量、推力作用和转速对飞行器稳定性响，采用自适应Newmark法，对系统横向振动响应进行分析，得到以下结论：

1)随着质量减少，系统固有频率、进动频率和临界转速逐渐增加，推力作用能够减小系统刚度，不考虑质量变化时，正进动和负反进动频率减小，推力和质量共同作用时，正进动和负反进动频率增大，说明质量消耗对进动频率影响大于推力作用。

2)当自旋转速小于临界转速时，受质量影响振幅减小；靠近临界转速时，振幅增加，等于临界转速频率时发生短暂共振，共振响应峰值最大时刻与转速重合时刻相比稍有延迟。