多元工具助推思维演进 以生为本构建深度学习

马骏　吴世彬

[摘 要]深度学习是一种学生学习动机深、参与程度深、思维层次深、运用水平深的学习模式。以小学数学“小数的性质”一课为例，提出了以核心知识和核心知识所蕴含的核心范式为载体，以给予学生充分的平台和空间为前提，遵从知识重演性、课堂发展性、习题的梯级性为指引，来说明和展示深度学习的教学设计的程序和方法。

[关键词]深度学习;小学数学;多元工具;验证反思;思维演进

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）05-0036-03

深度学习是在理解性学习的基础上，运用高阶思维学习新的思想，从而达成知识之间的整体性联通，是形成和发展学生核心素養的有效途径之一。对此，笔者设计了深度学习视域下的“小数的性质”一课，以课例来探讨深度学习的模式和路径。

一、探寻“学生起点”，明晰“理论脉络”

一方面，学生在学习小数的意义后，从小数的数位和计数单位的角度，丰富了对小数数域的理解，并通过数位顺序表将小数与整数进行了有效对接。这些都标志着学生的数的概念已从原本离散型的整数，扩展到具有稠密性的有理数。另一方面，学生已经具备了使用货币、长度单位等生活经历，以及用方格纸、数轴等直观数学模型来理解和表示小数与十进分数关系的能力。这些都是本课教学设计的“学生起点”。

深度学习的理念是本节课设计的“理论脉络”。深度学习区别于浅层学习被动、机械、以记忆为主的学习方式，是借助具有整合作用的实际问题来激活深层动机，展开切身体验和高阶思维，促进深度理解和实践创新，进而对学习者产生深远影响的学习样态。深度学习之“深”主要体现在学习动机深、参与程度深、思维层次深、运用水平深。

为了实现深度学习，笔者制订了这样的教学设计策略：分析知识形态的学科内容，捕捉核心知识和核心知识所蕴含的核心范式，并以此为载体，给予学生充分的发挥空间。例如，“小数的性质”的核心知识为小数的末尾添上“0”或去掉“0”，小数的大小不变;所蕴含的核心范式为，通过不完全归纳法，引导学生经历从具象到抽象，再到数学本质的过程，探索归纳出小数的性质。在教学过程中开展对学生探究精神和协作精神的培养，使之感受数学的理性之美和严谨之美，实现数学抽象素养的提升和逻辑推理素养的发展。

二、发现生活中的问题，多元工具开阔思路

深度学习讲求充分调动学生进行积极主动且批判性的学习。而从学生熟悉的领域里发现问题，如从末尾添1个“0”开始，逐步深入探讨，体现知识获得的重演性，是开展深度学习的妙法之一。

师：你们知道这是什么吗？（呈现微信红包的图片）你们抢过微信红包吗？昨天老师在发红包时遇到了这样的情况。（PPT显示：金额输入的是0.3元，系统显示的实时金额是0.30元）

师：这里的0.3和0.30相等吗？谁来证明？

生1：相等。可以通过元、角、分或长度单位的换算来证明，也可以通过画方格图来证明。

师：从这个例子中，你有什么发现？

生2：小数的末尾添上1个“0”，小数的大小不变。

师：数学是一门讲求严谨的学科，仅凭这一个例子，就代表所有的小数，大家觉得合理吗？应该怎么办？

生3：再多举几个例子。

师：我们刚才证明了0.3与0.30相等，你还想证明哪些小数相等？请大家借助锦囊里的工具来证明。

（学生举的例子以及证明方法如图1、图2、图3、图4、图5所示）

深度学习内容的设计要以学生为主体，找准学生的认知起点，给予学生充分的空间和平台，让不同水平的学生都深度参与到课堂活动当中。上述教学环节主要围绕小数的末尾添上1个“0”，小数的大小是否不变这个议题展开，教师引导学生运用了多种方法进行证明，目的在于：

1.让学生通过不完全归纳法来验证自己的猜想，体验科学的问题论证过程，感受数学学科严密的逻辑性，从而培养学生的严谨意识和质疑精神。

2.让学生通过自主化、多元化的实践操作来充分验证猜想，并在此过程中实现育人的理念，让学生感受到学习共同体的优势。

3.让学生在展示过程中实现依据生活经验举例证明，到借助直观的方格纸、数轴模型，再到抽象的数位顺序表的过渡，实现数学抽象思维逐步深化。

三、由点及面拓展深化，反思过程聚焦核心

要想有效拓展课堂的思维层次，促进学生深度学习的产生，就要建构发展性的课堂，引导学生从已知或已证明的理论中进行横向的拓展或纵向的深化，生成更加高位的结论。

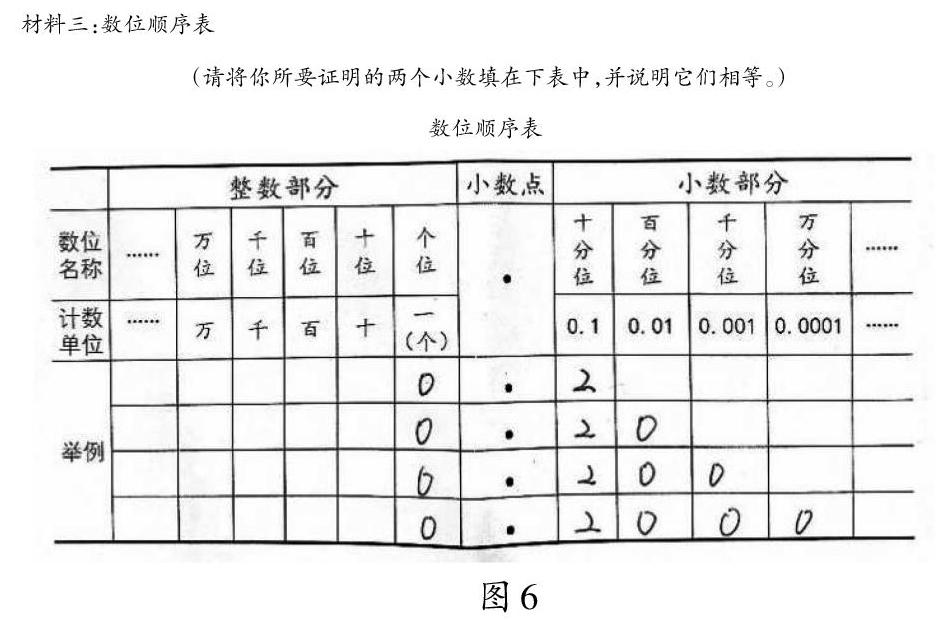
师：刚才我们证明了在小数的末尾添上1个“0”，小数的大小不变。有一位同学还试着证明了在小数的末尾添上多个“0”的情况（如图6）。

生1：我发现无论在0.2的末尾添上多少个“0”，2所在的数位都是十分位，也就是说，0.2表示2个0.1，0.20表示20个0.01，0.200表示200个0.001，等等，这些小数的大小都等于2个0.1，所以我觉得无论在小数的末尾添上多少个“0”，小数的大小都不变。

生2：小数的末尾添上 “0”，小数的大小不变。

师：数学的方法是多样的，观察的角度也是多样的，再仔细观察，你还有什么发现？

生3：我发现，正向看是添上“0”，反过来就是去掉“0”。可以总结为：在小数的末尾添上或去掉“0”，小数的大小不变。

师：大家所得出的这个结论就是小数的性质。

教师在得出在小数的末尾添上1个“0”，小数的大小不变后，趁热打铁由1个“0”拓展到多个“0”，由添上“0”，拓宽到去掉“0”，从而由零散的发现整理形成完整的结论。学生由此体会到了深入研究和多位思考的意义，为今后的学习积累了经验。

师：回顾一下，我们是如何发现小数的性质的呢？

生4：用了多种方法来证明，然后一步步推导出来的。

师：请大家评价一下用元、角、分换算和用米、分米、厘米换算这两种方法，你觉得怎么样？

生5：虽然好用，但不能表示所有的小数，特别是元、角、分。

师：那利用方格纸和数轴这两种方法呢？

生6：一目了然，都是图形，但我们手中的方格纸和数轴都不能表示所有小数。

师：那数位顺序表呢？

生7：用数位顺序表可以方便地表示出任意一个小数，而且可以方便地从数位和计数单位的角度发现，在小数末尾添上或去掉“0”，小数的大小不变。

数学方法的多元化，核心目的在于更好地实现知识的聚焦。学生在回顾比较的过程中再次经历了从生活化到抽象化的过程，并借助数位顺序表中的数位和计数单位，领悟到了小数具备这种性质的实质原因。同时，通过对各种证明方法的比较，让学生体验到科学的论证不仅要追求正确的结论，更要总结和反思证明的过程，要在多种方法中探寻更优的方法，这也是对学生方法论意识的渗透，真正达到了深度学习所追求的培养学生高阶思维的目的。

四、由“应用”到“运用”，设置梯级化习题

能够深入实践运用所学内容，是实现深度学习的重要一环。按照学生的实际学情，练习环节的设置要注重层次性、科学性、开放性和趣味性，既要围绕核心知识“循规蹈矩”，也要适当“推陈出新”。例如，笔者设计了下面的练习：

第一关：小数连连看。

第二关：小数来减肥。

第三关：小数点回家。

第四关：红包猜猜看。

提示1：它是一個两位小数，且小数部分有数字“8”。

提示2：红包里的钱只包含两个“0”，且只有1个“0”去掉后，大小不变。

提示3：所有数位上的数相加的和是10。

第一关和第二关是从正向的角度，考查学生对小数性质的理解与应用。第三关和第四关要求学生灵活运用小数的性质解决问题，而开放性的答案在提高了题目的难度和挑战性的同时，还提升了思维的深度。

在“小数的性质”一课中，笔者依据知识重演原理，引导学生从生活出发，对小数的末尾添上1个“0”小数的大小是否改变的问题，开展了基于经验的推理、基于图形直观的推理、基于小数意义的推理，并在此基础上，进一步延伸推导出小数的性质，体现了知识发展原理。再利用阶梯性的习题设置，引导学生运用所学知识，深化学习效果。

整个教学过程，由学生的发现而来，由学生的实践而证，由学生的交流而得，将深度学习的理念渗透其中。而多元方法的比较既是对过程的反思总结，又是对科学方法论的启发点拨。整节课经历了问题的发现，再到提出猜想—验证猜想—拓展结论—总结方法—运用结论的完整过程，体现了深度学习之要义，实现了面向全体学生、生成立体知识、建构活体方法，促进深度思考的教育教学目标。

[ 参 考 文 献 ]

[1] 付亦宁.深度学习的教学范式[J].全球教育展望，2017，46（7）：49-56.

[2] 马云鹏.深度学习的理解与实践模式——以小学数学学科为例[J].课程·教材· 教法，2017，37（4）：60-67.

[3] 喻平.小学数学深度学习的路向[J].教育视界，2019（4）：4-7.

（责编 吴美玲）