递归模型视角下数学概念理解的研究

方娜　吴华

[摘 要]数学概念理解是提升问题解决能力和高阶思维能力的基础，在数学教育领域至关重要。数学理解的递归模型为揭示概念理解过程提供了新视角。基于递归模型，遵循客观抽象与直观具体、历史顺序与“超回归”倒序、证伪与证实、行为实践与表达证明的设计准则，重构数学概念教学模型，促进数学概念理解。

[关键词]递归模型;数学概念理解;融通;分数概念教学

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）05-0024-03

在数学研究或数学教育中，数学概念理解一直是国内外讨论的重要话题。1989年全美数学教师理事会（National Council of Teachers of Mathematics，简称NCTM）明确提出：“数学课程的重点应该是‘数学概念和理解，数学教育研究者和教学设计者要将数学理解作为数学研究的首要重点。”《普通高中数学课程标准（实验）》指出：“在教学中应强调对基本概念和基本思想的理解和掌握，对一些核心概念和基本思想要贯穿高中数学教学的始终，帮助学习者逐步加深理解。”数学概念理解在数学学习活动中至关重要，但当前的概念教学却存在形式化的现象：引入概念时背景着墨不够，导致学习者对教学的内容、方法和意义知之甚少;以解题教学代替概念教学，本末倒置。

数学概念教学，关键是要细化数学概念的理解层级，揭示学习者对数学概念的理解进程，同时遵循客观抽象与直观具体、历史顺序与“超回归”倒序、证实与证伪、行为实践与表达证明有机融合的原则。课程开发者和教师可以根据数学概念理解的层级与原则来设计课程或组织教学。下面通过数学概念理解的递归模型和分数概念的实例分析，探索理解过程的新视角和概念教学的新策略。

一、数学概念理解及其递归模型

1.数学概念理解的内涵

在《辞海》中，“理解”是指了解、领会，深入解释为对新事物的认识是通过揭露事物间联系的过程。《全日制义务教育阶段数学课程标准（实验稿）》将“理解”解释为“能描述对象的特征和由来;能明确地阐述此对象与有关对象之间的区别和联系”。

数学学习中的概念理解，应由学习者對已学东西的意义不断更新、改造、组织、整理，建构有序的整体，从整体内部进行正逆向、交叉、跳跃式的联系，从总体中认识局部的、孤立的概念之间的内部联系，以抓住本质属性。数学概念理解的递归模型以崭新的视角，直观形象地揭示学习者进行数学概念理解的层次及条件。

2.数学概念理解的递归模型

（1）数学概念理解的递归模型简介

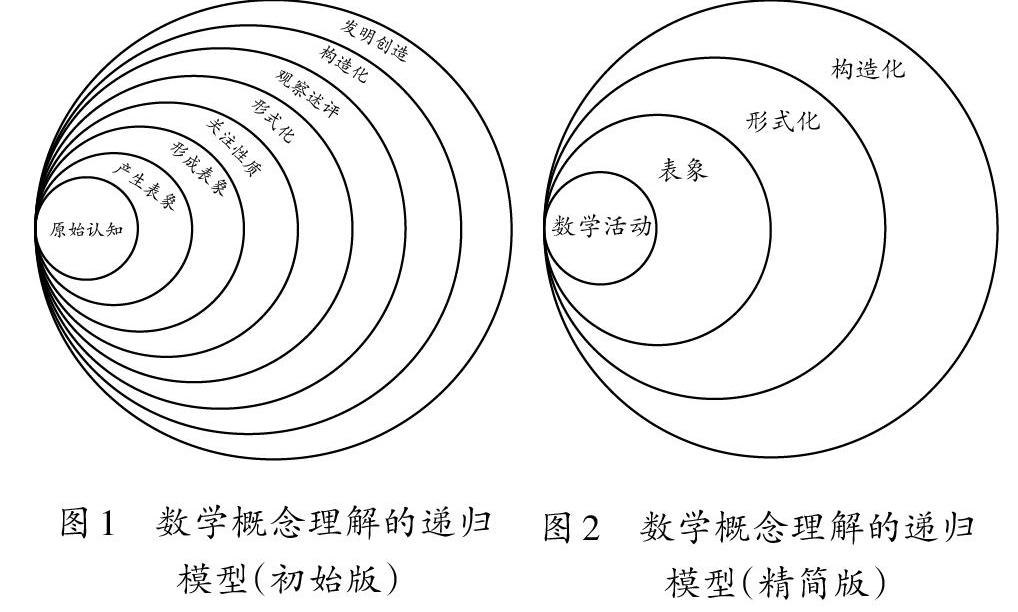
1989年，Pirie和Kieren结合认识与认识论障碍、概念定义与概念表象、多元表征、操作性概念与结构性概念等理论，提出了数学概念理解的递归模型。数学概念理解分为八个水平，分别为：“Primitive Knowing（原始认知）”“Image Making（产生表象）”“Image Having（形成表象）”“Property Noticing（关注性质）”“Formalising（形式化）”“Observing（观察述评）”“Structuring（构造化）”“Inventing（发明创造）”（如图1）。后继研究者又将八个理解水平精简为四个：数学活动、表象、形式化、构造化（如图2）。模型各个水平间“超越回归式”的相互包含，从认知的观点认为数学概念理解的增长非直线式的发展，而是一种整体的、有层次的、超越回归的心理过程，在这个过程中获得并应用一个静态的数学概念。

（2）数学理解的递归模型特点

超越性：外层理解水平包含和发展内层理解水平，并将内层理解水平协调统一。内层理解是外层理解的基础，外层理解是内层理解的升华。

回归性：这是数学概念理解的关键组成部分和核心特征。它揭示了理解过程的非线性，当在任何层级遇到不能立即解决的问题时，学习者需要返回到原有的、内在的层级，重建和完善对内在层级的理解，以支持、加深对外在层级的理解。这种返回的认知活动与最初的认知活动不同，它的水平更高、更有效。回归行为在深化数学概念理解的过程中并非都必要，回归的有效性取决于学习环境和学习者个人，特别是当学习者被鼓励折回内层收集特定的信息时，这种回归变得更有效，因为它带有目的性。

行为与表达的互补性：这是层次本身的结构特征，出现在“产生表象”“形成表象”“关注性质”三个层级中，超越原始认知的每一个层级都是由行动与表达的互补组成的。“参与”“回顾”“观看”“表达”“预测”和“记录”是数学概念理解由内层向外层的发展和过渡。

（3）概念数学理解的递归模型误区

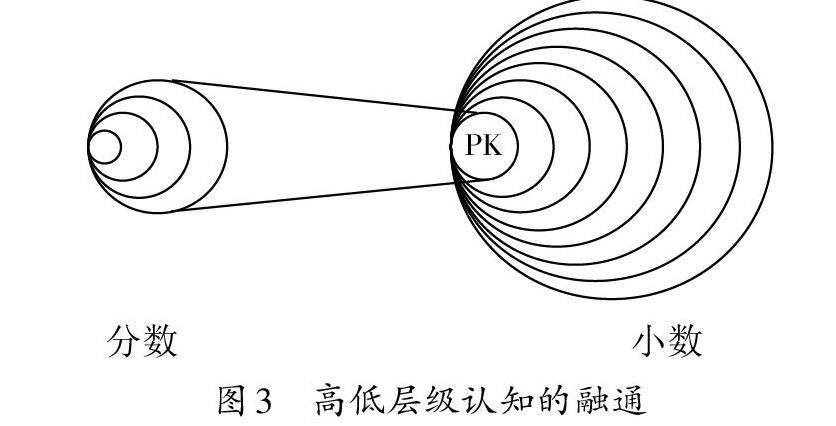
学习者对某一个数学概念的原始认知并非是最低级认知。在没有掌握基本概念之前积累的知识将被嵌入新的理解层次中。如图3，学习者掌握分数概念后，会将对分数概念的高层次认知作为理解小数的原始认知。

数学概念理解的递归模型的最外层被称为“发明创造”，并非学习者在其他层面上无“发明创造”：在“产生表象”层级，学习者能够根据学习内容，建构具有数学意义的实际情境，并对实际情境有合理的考量，这种“发明创造”更符合学习者的心智与认知。

二、递归模型视角下数学概念教学模型的重构

1.数学概念教学的策略

（1）数学概念教学体现客观抽象与直观具体的融通

数学概念从数量关系或空间形式来反映事物的本质特点，多以定义的形式表述，具有简洁性、概括性、抽象性。学习者在接触某个新的概念时，最佳的学习方法是通过模型直观和实践参与，产生和形成相关知识的表象。引入一个与原来概念相关的新概念时，灵活地把上一种概念的表征方式作为下一种概念呈现的表象，可提升对数学对象的关联性理解，实现概念不同表征方式间的融通，优化概念形成和概念同化过程。

（2）数学概念教学体现历史顺序与“超回归”倒序的融通

历史发生原理指出，个体知识的发生过程遵循人类知识的发展过程。近年来，将历史发生原理应用于数学教育，更是得到众多实证研究的肯定。“超回归”倒序，是指每当引入新的概念意义时，都应“超回归”到已学习过的原有概念的意义。为了使学习者理解数学概念的多种意义，教材编写和教学既要以数学知识发展为主线，将学科体系有机地融入教学设计中，又要兼顾个体对概念意义的理解具有“超回归”倒序的特点，允许存在学习上的反复，使学习者有时间、有机会对自己的思维活动进行反省，加深对新知识的理解。在进行外层次教学时要为学习者设计折回的机会，凸显新旧知识间的联系，引导学习者获得对数学概念的正确理解。

（3）数学概念教学体现证实与证伪的融通

证实就是证明一个问题的真实性。证伪思想则来源于波普尔的证伪主义。客观地说，证实只是部分解决了“是什么”和“为什么”，却不揭示“真”和“伪”之间的界限，而这一界限对学习者真正理解数学概念本质是十分必要的。在概念教学中，如何兼顾证实与证伪是研究者应当慎重思考的问题，适度设置伪命题，能使学习者明确真假命题的界限，掌握概念的性质。但过度设置伪命题，可能会诱导学习者的思维朝错误的方向发展。证伪与证实的融通将促进学习者理解概念的本质，推动理解进程向更高层发展。

（4）数学概念教学体现行为实践和表达证明的融通

理解和掌握数学概念需要花费大部分时间参与活动，发现、概括活动的规律，合作交流，解决相关问题。欧内斯特曾说：“数学知识的基础是对话，数学证明是一种特殊的叙事……证明是用来说服数学共同体中其他成员接受一个陈述或一组陈述为数学知识的一个文本。”根据数学概念理解的递归模型，“参与”“回顾”“观看”“表达”“预测”和“记录”是数学理解层级由内而外发展的过渡，在学习数学概念时，教师可给出数学表达式，由学习者设计具体情境下符合该数学表达式的问题并动手操作，实现数学意义与实际情境的双向建构，促进数学概念理解由最初的原始认知向最后的发明创造过渡。

2.数学概念教学模型的重构

基于数学”理解的递归模型和数学概念教学的策略，重构数学概念教學进程（如图4），即数学活动阶段、表象阶段、形式化阶段、构造化阶段。

三、 分数概念教学设计

1.递归模型视角下分数概念教学模型的重构

近20年，研究者对分数学习的关注点主要在分数基本概念的理解。在目前的研究中，有的学者着眼于分数定义研究，有的学者从教学与数学两个层面来探讨分数本质。不管从哪个角度展开研究，最终都要回到对分数意义理解这一基本问题上。因此，就小学分数的理解与教学而言，首先应探讨其意义。

J.Pack等学者根据分数意义的历史演变，将分数分为“部分/整体”“测量”“除法” “集合论”这四种意义（“集合论”的意义在小学阶段几乎不提及）。王光明等学者借鉴 Nurgul Duzenli-Gokalp和 Manjula Devi-Sharma 的思想，基于数学概念理解递归模型的内涵，构造出分数意义理解的数学概念理解模型（如图5），并指出分数的外层意义是建立在内层意义基础上的，综合与发展了内层意义，对内层意义的及时回顾，将有助于学习者学习新的分数意义。借鉴上述学者观点，笔者建构了融通历史顺序和“超回归”倒序的分数教学模型，如图6。

2.分数概念教学的策略

（1）创设数学与学习者生活结合点情境，感悟分数意义

在北师大版教材中，分数的学习最早出现在三年级上册，通过对“平均分割月饼”的认识，让学习者体会“部分/整体”的意义;在五年级，利用“丈量物体”的方式，让学习者初步感知分数的“测量”意义;在六年级，通过对“乘法的逆运算”等内容的学习，让学习者建立乘法与除法之间的运算关系，从而引出分数的“除法”意义。

（2）融通历史顺序和“超回归”倒叙，内化分数概念

分数意义演变的历史顺序，是指从低年级到高年级依次引入“部分/整体”“测量”“除法”三种分数意义。分数意义的“超回归”倒序表现为，在引入“测量”意义时，又对“部分/整体”意义进行了严格定义和再学习。在六年级引入“除法”意义时，又回归到了“部分/整体”与“测量”意义。例如，对“部分/整体”意义的回顾，主要运用数学实践活动（把一张纸的4/5平均分成2份），有助于增强学习者对“除法”意义的理解。这种顺序与倒序的融通，符合学习者对数学概念的理解进程与认知规律，从而更好地理解分数的概念。

（3）兼顾“证实”与“证伪”， 凸显分数本质

动态的数学观认为，数学教学应是由不确定知识到确定知识的渐进过程，在探寻结论的过程中，“证伪”起着非常重要的作用，在确定结论的时候，“证实”又发挥着不可替代的作用。在分数概念教学中，可适度设置如图7所示的问题，融通“证实”与“证伪”， 凸显分数本质。

（4）融通数学与生活，形成分数概念体系

分数概念可以表征多种相关但不同的意义，掌握分数概念的重要标志是不同层级意义的融通。在教学小数概念时，教师可引导学习者思考小数与分数的联系与区别，进行“超回归”倒序学习，更好地实现分数概念的高层次认知向小数概念认知的过渡，从而加深分数概念的理解，促进小数概念的获得。只有融通相关概念，融通数学与生活，才能形成数学概念体系，实现数学概念理解由原始认知层级向发明创造层级的过渡。

四、结语

数学概念理解的递归模型详细刻画了学习者进行概念理解的过程，为开展数学概念教学提供理论依据和策略引导。基于递归模型，实现数学概念的客观抽象与直观具体、概念意义的历史顺序和“超回归”倒序、概念逻辑的证伪与证实、概念体验的行为实践和表达证明之间的融通，就能促进学习者对数学概念的理解。

（责编 金 铃）