基于PSO-GRNN模型的夜光藻密度经验算法

李瑞东，宋金玲，刘 建，李警波

(河北科技师范学院数学与信息科技学院，河北 秦皇岛，066000)

赤潮是海洋中的浮游植物在特定条件下大量聚集并导致海水变色的一种生态灾害。近海赤潮的频繁暴发给海洋相关产业造成了巨大的经济损失，严重破坏了海洋环境，甚至危及人类的健康。因此，对赤潮开展预测研究有重要意义和实际应用价值[1]。赤潮形成的机理复杂，受环境影响较大，各因子之间表现出的关系为非线性关系，并且有关赤潮的样本数据较为缺乏，这些因素给赤潮的预测研究带来了一定的困难。由于神经网络对非线性函数有较强的逼近能力，近年来神经网络被广泛应用于赤潮的预测研究中[1～6]，其中，文献[1～4]根据海水理化因子数据建立了赤潮生物密度与环境因子的神经网络模型，间接实现对赤潮的预测，文献[5,6]根据影响赤潮发生的气象因素数据建立了赤潮等级预测模型。但是上述神经网络赤潮预测模型都存在对样本质量和数量要求高、预测稳定性差等问题，针对赤潮样本数据相对较少的情况适应性较差，因此有必要对基于神经网络的赤潮预测模型进行进一步的研究。

广义回归神经网络(GRNN)在样本数据量较少的情况下有着较好的回归预测效果，而且广义回归神经网络结构简单，只需要设定一个平滑因子σ，因此，广义回归神经网络的预测性能在很大程度上取决于σ的选择。一般情况下平滑因子σ作为先验知识或者凭借个人经验来手动设置，导致模型受人为主观影响较大、精度较差，如何优化平滑因子σ成为提高广义回归神经网络模型性能的关键问题。本次研究采用粒子群算法来获取广义回归神经网络的最优平滑因子，降低人为主观影响，提高广义回归神经网络的预测精度，得到改进后的PSO-GRNN模型；并根据夜光藻密度与环境因子的关系构建PSO-GRNN模型；最后通过实验对PSO-GRNN模型和其它模型的预测效果进行对比分析。实验结果证明，该模型对预测夜光藻密度具有一定的可行性。在实际应用中，根据夜光藻密度的预测值，对比赤潮发生时的夜光藻密度阈值，可以间接实现对赤潮的提前预测。

1 相关算法

1.1 广义回归神经网络(GRNN)

GRNN在结构上由4层构成，分别为输入层、模式层、求和层和输出层[7](图1)。

图1 GRNN网络拓扑结构

输入层的节点个数等于输入样本的特征维度，其作用是将训练样本的输入直接传递到模式层。

模式层的作用是对从输入层传递过来的训练样本进行学习，其节点个数等于训练样本的个数。学习函数见式(1)，其中X为模型的输入；Xi为第i个节点对应的训练样本；Pi为第i个节点的输出；σ为GRNN模型的平滑因子。

(1)

求和层的作用是对模式层的数据进行求和与加权求和，分别见式(2)和式(3)。其中SD为分母节点函数，SNj为分子节点函数，yij为连接权值。

(2)

(3)

输出层的节点数为训练样本中输出的特征维度，节点输出按照式(4)计算。

(4)

1.2 粒子群优化算法(PSO)

PSO是一种群体智能优化算法，其思想源于对鸟类捕食行为的模拟[8]。PSO用一群粒子来表示待寻优问题，每个粒子都有位置和速度两个属性，其中，每个粒子的当前位置代表问题的一个解。粒子的位置是不断变化的，粒子当前位置的好坏由适应度函数的值来衡量。

PSO算法首先初始化一群具有随机速度和位置的粒子和最大循环次数。然后执行如下循环：比较每个粒子当前位置与其自身历史最优位置pbest的适应度值，如果当前位置的适应度值较高，则把当前位置作为新的pbest；然后比较所有粒子的pbest与全局最优位置gbest的适应度值，如果某个粒子的pbest适应度值高于gbest适应度值，则把该粒子的pbest作为新的全局最优位置gbest。之后，每个粒子按照式(5)更新自己的速度、按照式(6)更新位置。当循环达到最大次数时，输出的全局最优位置gbest就是该问题的最优解。

Vi+1=wVi+c1r1(pbest-Xi)+c2r2(gbest-Xi)

(5)

Xi+1=Xi+Vi+1

(6)

式(5)中，Vi为第i次循环时当前粒子的速度；Vi+1为第i+1次循环时当前粒子的速度；式(6)中Xi为第i次循环时当前粒子的位置；Xi+1为第i+1次循环时当前粒子的位置；r1,r2分别为[0,1]之间的随机数；c1,c2为学习因子；w为权重因子。

2 基于PSO-GRNN的赤潮预测模型

GRNN模型通过MATLAB函数net=newgrnn(P,T,σ)来创建，其中P为训练样本的输入，T为训练样本的输出，σ为平滑因子。一般情况下平滑因子σ根据个人经验手动设置，导致模型学习效率低下、受人为影响较大。实际上平滑因子σ的选择可以看作寻优问题，即找到一个最优的σ，使得样本的输出值与实际值的误差最小。因此，可以采用PSO算法来选取GRNN模型最优的平滑因子σ，即将σ值视为粒子群中一个粒子的位置，从而找到σ的最优值。减少人为因素对GRNN模型预测结果的影响，提高GRNN模型的泛化能力。PSO-GRNN模型流程如下：

①设置粒子群的规模、最大循环次数等参数，随机初始化各粒子的速度和位置。其中，把GRNN模型的平滑因子σ作为粒子的位置，将GRNN模型看作适应度函数，将模型的决定系数作为PSO算法的适应度函数值。因此，适应度函数值越高，表示该模型输出的预测值与实际值的误差越小。

重复执行②～④步，直到达到最大循环次数为止。

②计算当前各粒子当前位置的适应度值，然后与其自身历史最优位置pbest的适应度值进行比较，如果当前位置的适应度值较高，则把当前位置作为新的历史最优位置pbest。

③比较当前所有粒子的历史最优位置pbest的适应度值，找出对应最高适应度值的位置，将其作为全局最优位置gbest。

④根据式(5)(6)更新粒子的速度和位置。

⑤当达到最大循环次数时，将搜索到的全局最优位置gbest作为平滑因子σ构建的GRNN模型即为PSO-GRNN模型，见式(7)。

net=newgrnn(P,T,gbest)

(7)

3 实验及结果分析

3.1 PSO-GRNN模型构建

为了验证PSO-GRNN模型的预测效果，采用文献[3]中的样本数据(表1)，通过夜光藻密度和海水各种理化因子之间的相关性[9]构建PSO-GRNN模型，其中将水温、溶解氧、盐度、总氮、可溶性无机磷、浮游植物密度作为模型输入，将夜光藻的密度作为模型输出。

表1 实验采用的样本数据

(8)

首先，利用PSO算法找出GRNN模型最优的平滑因子σ。初始化种群数量为30，权重因子=0.5，最大速为0.01，最小速度为-0.01，学习因子c1=c2=2，最大循环次数为20，粒子位置的区间为(0,1)，随机初始化各粒子的速度和位置。将表1中第1～24组归一化样本数据作为GRNN模型的训练样本，按照前述本次研究的PSO-GRNN模型流程的②～④步不断循环更新σ值，直到循环次数达到最大为止。

开始优化时，适应度值很低，当循环到第3次的时候，曲线开始迅速上升(图2)。随着进化次数的增加，曲线变得越来越平滑，当循环到第12次之后，PSO的适应度值达到了最高并趋于稳定，说明此时模型已经达到了最优，此时对应平滑因子σ的值为0.083 3。

图2 PSO优化平滑因子σ的过程曲线

然后，采用表1中前24组归一化样本数据和上一步中挑选出来的最优平滑因子0.083 3训练GRNN模型，即得到训练好的PSO-GRNN模型。最后，将表1中第25～28组归一化样本数据作为预测样本导入训练好的PSO-GRNN模型中进行预测。实验结果表明，PSO-GRNN模型的预测值和实际值比较接近，最大误差为12.45，最小误差仅为1.04，平均误差为6.605(表2)，预测样本的均方根误差(RMSE)为7.99。

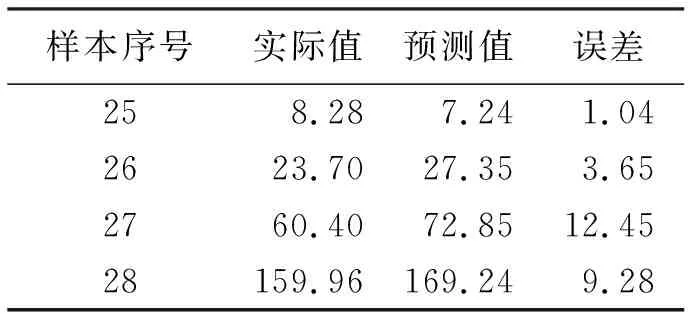
表2 PSO-GRNN 模型预测结果

3.2 PSO-GRNN模型预测效果与其它模型预测效果对比

为了进一步验证PSO-GRNN模型的预测效果，采用目前使用最广泛的BP模型、RBF模型、GRNN模型与其进行预测效果对比分析。本次依然使用表1中第1～24组样本作为训练样本，分别对各个模型进行训练，然后利用25～28组数据进行预测。实验结果表明，BP模型和RBF模型都存在个别预测值与实际值相差悬殊的情况，GRNN模型虽然没有相差悬殊的情况，但整体误差依旧较大，说明PSO-GRNN模型的预测结果相对BP模型、RBF模型、GRNN模型误差更小、更加精确(图3)。

图3 各模型预测值和真实值的对比

表3 各模型的均方根误差

(9)

4 结 论

针对传统神经网络模型对样本的质量和数量要求高、预测稳定性差等问题，笔者使用对样本质量和数量要求不是特别高且相对稳定的广义回归神经网络来建立夜光藻密度预测模型，并采用粒子群算法来获取最优的平滑因子，可减少人为因素对预测结果的影响。通过实验得出PSO-GRNN模型的均方根误差值仅为7.99，远低于BP，RBF和GRNN模型的均方根误差值，为赤潮的预测研究提供了新的解决方案。