最大度为5的哈密顿图的星边色数

王 莹，申玉发，肖 宏，周 雪

(河北科技师范学院数学与信息科技学院，河北 秦皇岛，066004)

图的染色理论是图论中很重要的研究课题。应解决实际问题的需要，在经典图的顶点染色和边染色的基础之上，衍生出了一些带有限制条件的边染色问题，如图的强边染色和星边染色等问题。

定义1[1]图G的一个正常k-边染色是指一个映射φ∶E(G)→{1,2,…,k}，且对E(G)中任意两条相邻的边e1,e2都满足φ(e1)≠φ(e2)。

以下介绍两种有约束条件的边染色的定义。

定义2[2]图G的一个强k-边染色是G的一个满足任意两条距离至多是2的边染不同颜色的正常k-边染色。若图G有一个强k-边染色，则称G是强k-边可染的。图G的强边色数是使G有一个强k-边染色的最小非负整数k，用χs′(G)来表示。

定义3[2]图G的一个星k-边染色是G的一个满足任意长度是4的路或圈至少用3种颜色染色的正常k-边染色。若图G有一个星k-边染色，则称G是星k-边可染的。图G的星边色数是使得G有一个星k-边染色的最小非负整数k，用χst′(G)来表示。

根据定义可知，图G的星边色数与强边色数之间有如下关系式[2]：

χst′(G)≤χs′(G)

强边染色的概念是Fouquet等[3]在1983年为解决无线电通信网络中的信道分配问题而提出的。1989年，Erdös等[4,5]提出了一个关于图的强边色数上界的猜想：对于任意的图G，当图的最大度Δ为偶数时，有χs′(G)≤1.25Δ2；当Δ为奇数时，有χs′(G)≤1.25Δ2-0.5Δ+0.25。之后，学者们围绕着这个颇具挑战性的猜想做了大量的研究工作，也取得了一系列的成果。2015年，Zang[6]证明了下面的引理。

引理1每个最大度是5的图都是强37-边可染色的。

由于到目前为止，关于最大度为5的图的星边色数的上界还没有相关结果，因此想要确定这种图的星边色数，就只能借助上面的星边色数与强边色数的关系式和引理1，由此两者可知，最大度为5的图是星37-边可染的。

星边染色是刘信生等[7]在星点染色的基础上于2008年定义的。同时，他们给出了一般图的星边色数的一个上界：若图G是Δ≥7的简单图，则有χst′(G)≤[16(Δ-1)3/2]。因为星边染色的概念比强边染色概念的提出晚了20多年，所以人们目前对于星边染色的研究并没有强边染色研究的深入，围绕图的星边染色的结果相对较少。

2013年，Mohar等[8]研究了完全图、子立方图等的星边色数，并证明了下面的引理。

引理2每个最大度为3的图都是星7-边可染色的。

2019年，王莹[2]证明了最大度是4的图都是星14-边可染的。

本次研究主要围绕图的星边染色问题展开，通过对图的结构进行分析，再运用边分解的方法，证明每个最大度为5的哈密顿图是星22-边可染的。

首先，笔者给出证明中所用到的术语和定义。本次研究考虑的图是有限简单图。设V(G)表示图G的顶点集、E(G)表示G的边集，而Δ(G)，δ(G)分别表示G最大度和最小度[9]。通常用u和v表示G中的两个点，用e表示G中的一条边，若e可以用等式e=uv表示，则称点u和v是边e的端点，也可以叫做u和v相邻[2]。如果两条边与同一个点关联，此时就把两条边叫做相邻的。用NG(v)表示与点v相邻的点集合，用dG(v)=|NG(v)|表示点v在G中的度。用dG(u,v)表示连接2个点u和v的最短路的长度，即它们在G中的距离。在不引起混淆的情况下，分别将Δ(G)，NG(v)，dG(v)，dG(u,v)简记为Δ，N(v)，d(v)，d(u,v)。一个k-点是一个度数为k的点。对i≥1，用ni(v)表示与点v相邻的i-点的个数。图中两条边的距离是指对应线图中相应两点之间的距离。若两条边相邻，则称这两条边的距离为1。若两条边不相邻，但这两条边有公共邻边，则称这两条边的距离为2。

对于图G的一个非空的边集E′⊆E，通常用F-E′表示从G中删去E′中所有的边而得到的子图[10]。G的一个由边集E′导出的边导出子图G[E′]是以E′为边集，以至少与E′中一条边关联的点的全体为点集的图。

一个含图G的每一个顶点的圈被称为G的一个哈密顿(Hamilton)圈[1]。显然，G的一个哈密顿圈是G的一个生成圈。一个含有哈密顿圈的图称为哈密顿图[9]。由定义可知，圈Cn是哈密顿图，完全图Kn是哈密顿图。

若将G分解成子图G1,G2,…,Gm使得E(G)=E(G1)∪E(G2)∪…∪E(Gm)，且当i≠j时，有E(Gi)∩E(Gj)=∅，则称其为图G的一个边分解。

以下笔者将重点研究最大度是5的哈密顿图的星边染色问题。

定理1若G是一个最大度为5的哈密顿图，则有χst′(G)≤22。

证明设G是Δ(G)=5的哈密顿图，根据定义可知G必是连通的。用G2表示G的一个哈密顿圈，显然，G2⊂G。这样，图G中的边就被分成了两类：哈密顿圈上的边和不在哈密顿圈上的边(哈密顿圈的弦)。将不在哈密顿圈G2上的边组成的集合的导出子图记为G1，则有E(G)=E(G1)∪E(G2)，E(G1)∩E(G2)=∅且Δ(G1)≤3。用C={1,2,…,22}表示一个颜色集合。按如下方法给出图G的一个星22-边染色φ。

步骤1用C1={1,2,…,7}中的7种颜色对G1中的边进行星边染色。

根据引理2，由图G1满足Δ(G1)≤3，得G1是星7-边可染的，因此，这个染色是可行的。

步骤2用C2={8,9,…,22}中的15种颜色对G2中的边进行星边染色。

在这一步骤中，将用颜色集合C2对G2中的边进行贪婪染色。设|E(G2)|=n，对G2的边按逆时针顺序进行如下标号：e1,e2,…,en，并且将e1,e2,e3的顶点分别记为b,,a,c,d。为使叙述简洁，在考虑对边ei∈E(G2)，i=1,2,…,n，进行染色时，将与ei距离为2的且有弦作为公共邻边的边称为ei的禁用边，将ei的禁用边上所染的颜色组成的集合记为F(ei)。e1′,e2′,e3′,e4′,e5′,e6′既是边e1的禁用边，也是边e2的禁用边(图1)。因为，对于任意的边ei至多有12条禁用边，所以|F(ei)|≤12。

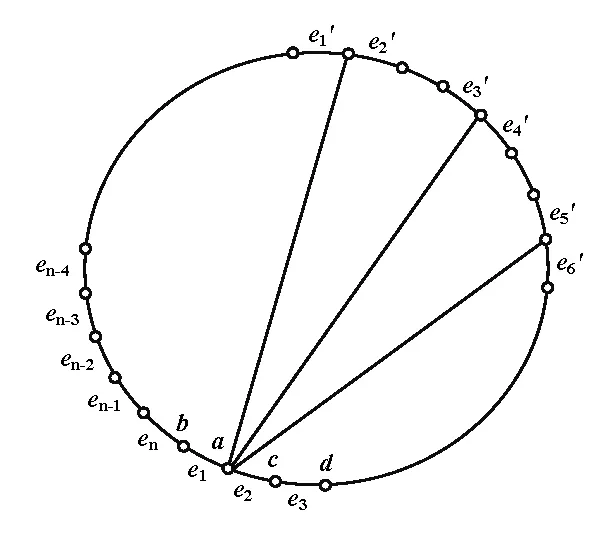
图1 哈密顿图

现在按角标顺序对G2中的边进行染色：

先染色边e1，此时，由于e1的禁用边都没有染色，用颜色8来染e1，即φ(e1)=8。

再染色边e2，只需回避e1所染的颜色，不妨用颜色9来染色边e2，即φ(e2)=9。

再染色边e3，只需回避e1和e2所染的颜色，不妨用颜色10来染e3，即φ(e3)=10。

…

再染色边ei(4≤i≤n-2)时，只需回避|F(ei)∪φ(ei-1)∪φ(ei-2)|≤14种颜色，由|C2|=15，知边ei可以染好。

再染色边en-1，需回避|F(en-1)∪φ(en-2)∪φ(en-3)|≤14种颜色。

最后，染色边en，根据φ(en-1)和φ(e1)是否相等分别进行讨论：

情况1φ(en-1)≠φ(e1)

染色边en时，只需要回避|F(en)∪φ(en-1)∪φ(e1)|≤14种颜色，就可以得到图G的一个星22-边染色。

情况2φ(en-1)≠φ(e1)=8

令A=F(en)∪φ(en-2)∪φ(e1)∪φ(e2)=F(en)∪φ(en-2)∪{8,9}，根据在染色时边en是否有可用色，分以下两种情况进行讨论：

情况2.1A≠C2

用C2-A中的颜色染色边en，就可以得到图G的一个星22-边染色。

情况2.2A=C2

此时|A|=15且集合中的任意两条边都染了不同颜色，再考虑是否可以改染边e1：

情况2.2.1若F(e1)∪φ(e1)∪φ(e2)∪φ(e3)=F(e1)∪{8,9,10}≠C2，则可以用在C2中却不在F(e1)∪{8,9,10}中的某颜色改染边e1，改染后即回到情况1。

情况2.2.2若F(e1)∪{8,9,10}=C2，则|F(e1)∪{8,9,10}|=15，先用颜色10改染边e1，并且将改染后的颜色记为φ′(e1)，再考虑如何染色边en。若F(en)∪φ′(e1)∪φ(en-1)∪φ(e2)=F(en)∪{8,9,10}≠C2，此时，就回到了情况2.1。若F(en)∪{8,9,10}=C2=A，即φ(en-2)=10。此时，用颜色α∈C2-(F(e2)∪{9,10})改染边e2，再将边e1改染为9，即可回到情况1。

为了进一步说明运用以上方法得到的染色φ是图G的一个星边染色，下面运用反证法来进行证明。

假设图G中有一条长度为4的路(或者圈)上的连续的4条边分别染色为αβαβ，其中α,β∈C。根据以上方法制订的染色规则，颜色α和β不能同时属于集合C1或C2。不失一般性，不妨假设α∈C1，由距离为2的两条禁用边一定染不同染色，知β∈C2必不成立。证毕。

结论每个最大度为5的哈密顿图都是星22-边可染的。