基于软件无线电与神经网络的频谱监测识别系统

覃远年，谢旭锋，刘 申

(桂林电子科技大学，广西 桂林 541000)

0 引言

随着5G即将投放市场，频谱监测工作也将面临海量无线数据的严峻考验。现有的城市频谱监测主要依赖于固定监测站，由于设备启动成本高和信号识别依赖人工等因素，只能在某些时间段监测频谱使用情况，这种方式缺乏对频谱环境的持续性监测，并且只能对有限的热点区域监测。因此如何解决频谱监测成本高、持续性差和信号识别依赖人工等问题已经迫在眉睫。

针对频谱监测成本高、持续性差的问题，目前许多学者提出可利用软件无线电平台，搭建低成本小型可移动监测站，方便手持或无人机装载[1-5]。李晓光等利用GNURadio软件无线电平台搭配USRP设备，解决了信道色噪声造成噪底不平坦条件下的宽带信号检测问题[6]。但是软件无线电平台自身很难承担繁重的计算任务，无法进一步深入开发。刘玉军等利用无人机对空中频谱进行监测，并设计了一种根据频谱环境，无人机自主规划路径的方法[7]，但没有提及如何处理无人机采集的频谱数据。

而针对信号识别依赖人工的问题，目前信号识别主要通过无线电信号特征(中心频率、带宽、码率和调制方式等)，利用模式识别的方法进行信号识别。且现有的信号识别对象都是调制信号，没有考虑到实际更为复杂的无线通信环境对信号产生的影响以及信号的其他编码和发送信息等的差异对信号频谱的干扰等[8]。因此，需要结合实际通信环境综合考虑研究信号识别方法。同时现有检测站在对异常频谱判定方面依然依赖于人工或仪器。而深度学习神经网络在面对不断更新变化的无线通信环境时，其强大的“学习能力”无疑具有较大优势[9-14]。无线电监测系统采集到的大量数据，可以经移动网络或WLAN传输至云端，通过云端服务器中搭建的神经网络，对其进行训练，即可识别不同环境下的各种信号类型或频谱状态。冯浩等利用Hadoop云计算平台和HBase分布式数据库，对无线电频谱监测数据进行管理和存储[15]。但没有对频谱数据进行识别分析。方宁等针对现有的时域模态参数识别方法大多存在难定阶和抗噪性差的问题，提出一种无监督学习的卷积神经网络(CNN)的振动信号模态识别方法[16]。蒋兵等利用PNN神经网络解决了雷达信号调制类型多样且识别成功率较低的问题[17]。但这些方法大多也都是针对单一类型的信号进行识别，而并非对某段频谱进行识别，反应其状态信息。

本文利用软件无线电和BP神经网络，设计了一套无线电监测系统。首先运用GNURadio软件无线电平台，采集实时的固定区域某一频段的频谱波形，通过无线网络传输给云端，利用云端服务器的神经网络和主成分分析(PCA)等算法做进一步的信号识别处理[18-19]。

1 GNURadio频谱扫描

目前，常用的软件无线电软件有GNURadio，LABVIEW，Vanu Software Radio等。本文选择使用开源并拥有强大交互社区的GNURadio作为系统开发平台。

利用GNURadio自带程序以及NI公司提供的扩展包中的实时扫频程序进行频谱检测工作，程序框图如图1所示。该程序可以扫描50 MHz～6 GHz的频谱，并采集指定频段的时域I/Q数据，再通过 FFT转换获得频域数据。

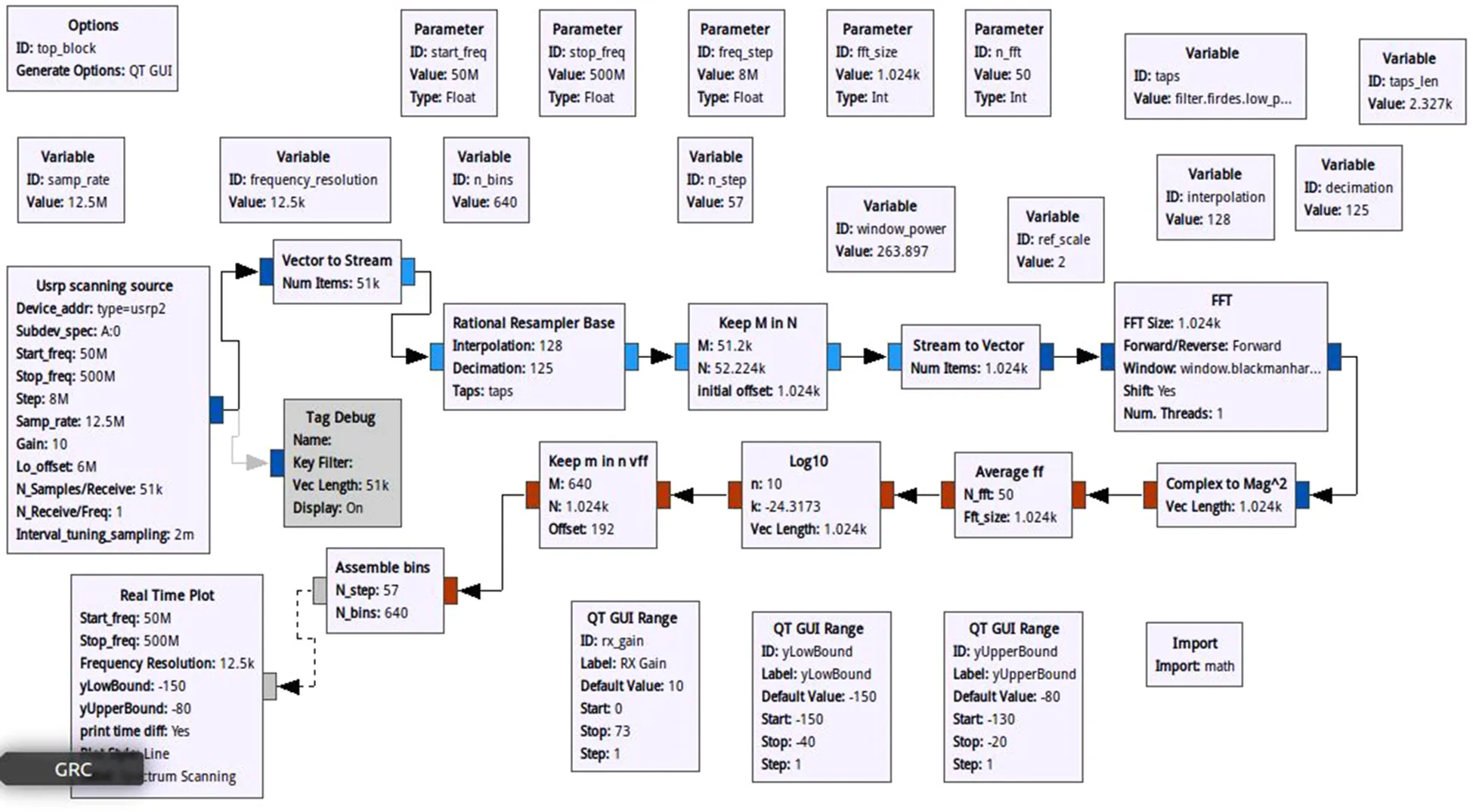
图1 GNURadio实时扫频程序框图Fig.1 GNURadio real-time scanning spectrum block diagram

之后，经FFT转换的频谱数据通过数据类型和单位转换可以实时显示，如图2所示。图2中心频率为2 440 MHz、功率为-28 dBm的信号。

图2 实时频谱图Fig.2 Real-time spectrogram

2 训练样本预处理

2.1 训练样本分类

2.4 GHz公有频段信号种类繁多，常见的有WiFi，Bluetooth，ZigBee等。目前该频段被分为14个信道，每个信道带宽为22 M。一般常用1,6,11三个信道，原因是这3个信道没有频率重合，互不干扰。为了构建神经网络频谱识别系统，以20 M，40 M带宽的2种不同WiFi信号进行实验，频谱数据作为训练样本，人为制造出6类频谱状态，如表1所示。

表1 6种不同的频谱状态
Tab.1 Six different spectrum states

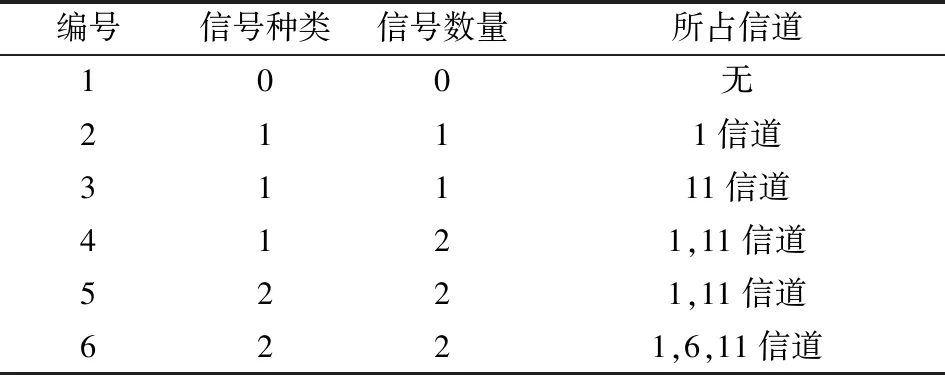
编号信号种类信号数量所占信道100无2111信道31111信道4121,11信道5221,11信道6221,6,11信道

每种信号采集500个样本，6类波形共3 000个样本作为训练集。再以不同于训练集且不同时刻的这6类波形，每类波形200个样本，作为测试集。

在构建神经网络之前，需要对导入的数据进行预处理，采用PCA+归一化处理的组合预处理方法，以便神经网络能以更高的效率进行训练且拥有更高的识别率。

2.2 监测设备前端预处理

需要说明的是，扫频程序不能在一个时间节点完成整个2 400～2 490 M频率区间的扫描工作，也就是说，单个时间节点(本程序中，样本的产生频率不与采样率挂钩，而是由模块底层程序和硬件决定)的数据无法还原频谱此时刻的完整信息。

取相邻10个时间节点的数据组成一个完整的频谱，频谱中每个频点的取值为这10个时间节点中该频点的概率密度极大值，样本数据如图3所示。

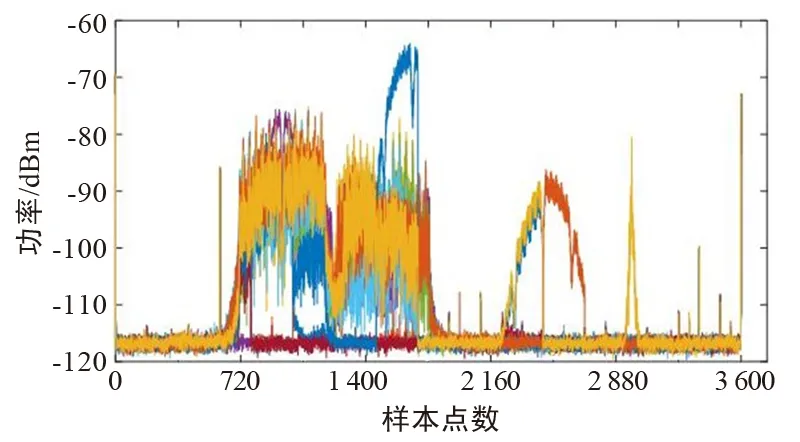
图3 未预处理的频谱数据图Fig.3 Unpreprocessed spectrum data map

图3中的频谱数据量较大，同时频谱状态较为杂乱，存在个别持续时间极短的信号。通常在干扰排查工作中，这种占用信道时间极短的信号可以忽略不计。如果直接用此数据训练，会影响神经网络计算效率和识别效果。因此设计了一种针对此频谱数据的预处理算法，具体步骤如下：

① 减少样本的数据量，利用ksdensity函数求出横坐标上每个采样点的概率密度曲线；

② 求出该曲线各个极大值点的横坐标和概率；

③ 设定概率阈值为0.1，以滤除占用信道时间极短的信号；

④ 保留每个采样点中拥有最大功率的极大值点。

经过预处理后的频谱数据如图4所示。虽然由于阈值的设定使信号有所失真，但大体保持了原有信号的波形和带宽，不会对神经网络的识别工作造成太大的影响。同时，样本数据量减少90%，且消除了个别持续时间极短的信号，提取了主要的有效信息：波形、信号带宽和信号频率。对比图3和图4，可以发现图3中第1 400～第1 800个采样点处有一段不完整的信号波形，通过预处理算法后成功滤除。

图4 预处理过后的频谱数据图Fig.4 Spectrum data after pre-processing

由于此算法没有较大的计算量，因此决定借鉴边缘计算的思想，将其计算任务安排在监测设备前端。目前，大部分软件无线电设备都搭载了FPGA或ARM芯片，具有一定的计算能力。这样既降低了云端计算的压力，又能减少数据传输所带来的时延。

在神经网络训练之前，还需要对导入的数据做进一步预处理，采用PCA+归一化处理的组合预处理方法，以便神经网络能以更高的效率进行训练且拥有更高的识别率。

2.3 主成分分析

PCA的原理是以损失次要信息为代价，通过低维表征的向量和特征向量矩阵，重构出所对应的原始高维向量。

本文需要神经网络进行识别的频谱状态共有6种，每种频谱状态以10份不同的波形数据作为训练样本，每个样本由其功率值组成一个向量xi，则样本的采样点数量为xi的维数，采样的频点数为3 600，可得训练样本集为{x1,x2,…,xM}，平均向量为：

(1)

对训练样本集进行去均值，即：

(2)

再求出对去均值后的训练样本集的协方差矩阵：

(3)

之后求出协方差矩阵的特征向量ui和对应的特征值λi，并将协方差矩阵的特征值按大到小排序，选择其中最大的k个，将其对应的k个特征向量分别作为列向量组成特征向量矩阵Wk。最后，计算xnew·Wk，即将数据集xnew投影到选取的特征向量，得到已经降维的数据集P=xnew·Wk。选取最大的前k个特征值λi，即维数从3 600减少至k，k最佳取值将在实验部分给出。这样既保留了数据的主特征，又能大大提高神经网络的训练效率。

但这些特征数据的单位、数量级并不相同，使神经网络收敛慢且训练时间长。因此还需要对P做归一化处理。

2.4 归一化处理

除了加快神经网络的训练速度，归一化还可避免可能出现因数据范围原因导致输入作用变化的情况。同时，神经网络输出层的激活函数设计也要符合要求，其值域受到制约，输出数据值域要与其保持一致。若采用对数S形激活函数，其值域是(0,1)，输出的数据也必须在(0,1)，所以归一化到[0,1]区间。同时，S形激活函数在值域之外过于平缓，丧失了区分能力。在做归一化处理之前，将所有整理好的数据集P重新组合成一个新的矩阵：

H=P={x1·u1x2·u2…xk·uk}。

(4)

对每一行相同数据类别的数据进行归一化处理，同时也减少了之后神经网络输入端的数量。选用mapminmax函数对之前得到的数据集P做归一化处理。mapminmax函数的计算公式为：

y=(ymax-ymin)*(x-xmin)/(xmax-xmin)+ymin，

(5)

式中，ymin，ymax为归一化的值域范围，其值取决于输出层的神经网络激活函数。本文选取的输出层神经网络激活函数为双曲正切 S形函数，其值域范围分别为[-1，1]，设ymin=-1，ymax=1。

对于之前得到的输入矩阵H，mapminmax函数逐行计算，如计算一行任意数据{z1，z2，...，z60}时，假设此行中最小值为z1，最大值为z2，归一化z60时的计算公式可化为：

y=2*(-z2)/(z1-z2)-1。

(6)

3 搭建BP神经网络

目前，搭建神经网络的软件平台日趋成熟且专业化。如TensorFlow，NeuroSolutions，Matlab等。虽然TensorFlow在各方面都显得更为优秀，但Matlab的优势在于支持GNURadio采集到的数据格式。由于基于信号频谱数据的识别系统并不复杂， 选用较为简单的BP神经网络，从而减少相应的计算复杂度。

BP神经网络训练过程中会产生反馈信号，在分类过程中数据向前传送，直到到达输出层，不同于复杂的后馈网络，层间没有向后的反馈信号，因此被称为前馈网络。

图5为构建的前馈神经网络，其中第1层为输入单元，第2层为隐含层，第3层为输出层。由于输入的数据是一个经过归一化二维矩阵，所以输入向量的最小值为-1，最大值为1。基于分类的要求，隐含层被设计为一层；输出层的神经元数量和分类数量保持一致，为6个。输入层和隐含层的神经元数在实验部分进行讨论。

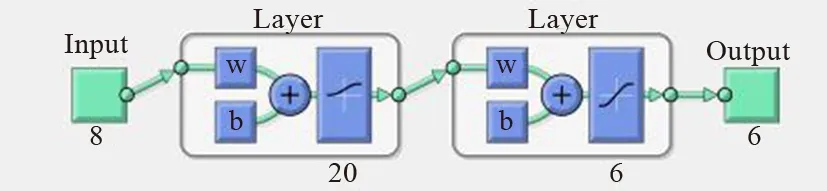
图5 神经网络结构Fig.5 Neural network structure

在神经网络中，神经元是最基本的单位，图6中x1～xn为从其他神经元或输入单元传来的输入信号，wiv表示从神经元v到神经元i的连接权值，θ表示一个阈值。神经元i的输出与输入关系为：

(7)

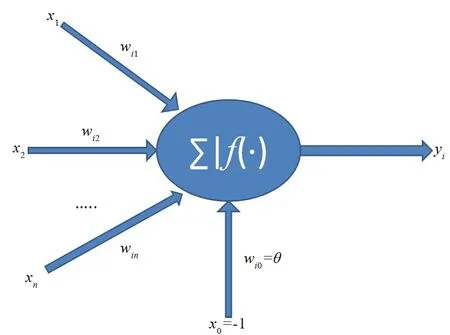
图6 神经元结构Fig.6 Neuron structure

图6中，yi表示神经元i的输出，函数f称为激活函数，net称为净激活。激活函数是神经网络中重要的一环，一般常用的有线性函数、斜面函数、阈值函数和S形函数等。由于对数S形函数与双曲正切S形函数具有可导的性质，适合于BP神经网络，因此选用对数S形转移函数作为隐含层神经元的激活函数，双曲正切S形转移函数作为输出层神经元的激活函数。这2种激活函数的公式如下：

(8)

在开始训练之前，还需要设置一些其他的参数。训练的最大迭代次数Epoch为1 000；初始训练学习率lr为0.1；训练性能学习目标goal为0.001；常用的MSE作为性能指数。

学习函数选用traingdx函数。traingdx是一个网络训练函数，它根据梯度下降动量和自适应学习速率来更新权重和偏置值。traingdx将自适应学习率与动量训练相结合，其动量系数mc作为附加的训练参数。traingdx可以训练任何网络，只要其权重，净输入和激活函数可导。反向传播用于计算相对于权重或偏差变量X的性能指数pref的导数。每个变量根据具有动量的梯度下降进行调整。

(9)

式中，mc默认取值为0.9，dXprev是之前权值或偏差的变化量。对于每次迭代，如果性能指数pref朝着目标减小，则学习率因子lr_inc增加。如果性能增加超过因子max_perf_inc=1.04，则学习速率由因子lr_dec调整，且不会增加性能；并设置内置sim函数作为网络预测输出函数。

4 实验与讨论

本文中设置3组测试实验，第1组为验证PCA算法保留的最佳特征维度，设置常用的波幅分析作为对比组；第2组则为了体现出本文中预处理方法的性能优势，仿真实验分为PCA+归一化数据预处理组和仅归一化组两组，作为对照实验。以隐含层的神经节点数作为自变量，对比二者的识别率。

如图7所示，以100个样本为测试集，对训练完成的BP神经网络进行了测试，此时PCA算法处理后的样本特征维度为17，隐含层神经节点数为20。可见此次识别效果极好，识别率高达97%。

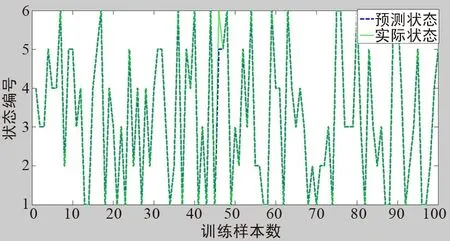
图7 BP神经网络识别率测试Fig.7 BP neural network recognition rate test

对于第2组实验，选择在隐含层设置20个神经节点。在Matlab中，PCA函数在处理样本数据后给出了17个主成分特征维度。对于文中识别的6类波形数据，数据特征的差异主要存在于信号数量、信号带宽、信号频率和信号强度4个方面。相对于PCA算法，波幅分析借鉴判决树的思想，分析和抓取最主要的数据特征。

如图2所示，检测设备的底噪约为-97 dBm，因此本次仿真中将-80 dBm作为判定频谱波形是否为信号的阈值。对于本文的数据集，选择了以下8项具有区分能力的特征：功率方差、最大功率、最大功率点频率、平均功率、功率超过阈值采样点总数、功率超过阈值频点频率平均值、功率超过阈值连续区域个数以及功率超过阈值连续区域所有采样点频率之和。当然，每项特征之间的区分能力是有差异的，实验随机选取n项作为特征维度。

由图8分析可得，在所用特征维度较小时PCA算法优势明显，波幅分析识别率较低。在特征维度为5时，PCA算法和波幅分析的识别率曲线斜率趋近于0。因此，使用PCA算法后只需保留前5项特征值即可。相较于波幅分析，虽然PCA算法在达到一定维度后的性能优势不算明显，但在实际中面对复杂的频谱波形时，泛用性明显强于需要区分特征的波幅分析。

图8 信号识别率随特征维度变化曲线Fig.8 Signal recognition rate as a function of dimensional dimension

在第3组实验中，如图9所示，隐含层神经节点数对2种预处理方法识别率的影响几乎相同，在一定范围内识别率随神经节点数的增加而增加，在神经节点数等于14时，再继续增加神经节点数，识别率则基本保持在一定水平没有太大波动。未处理的数据特征维度高达3 600，虽然识别率略高于经PCA处理后的数据，但时间复杂度方面，则明显要高出PCA许多。

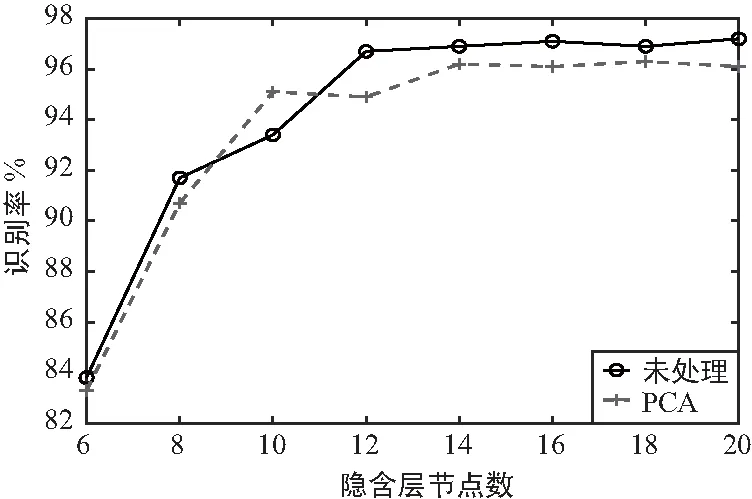
图9 信号识别率随隐含层节点数变化曲线Fig.9 Signal recognition rate as a function of the number of hidden layer nodes

值得一提的是，未经PCA处理的数据训练时，在少数情况下会陷入局部最优，导致性能指数无法达到学习目标，同时性能梯度变化也不明显，从而使学习函数 traingdx只能通过达到最大迭代次数停止，也就是说这会使神经网络的运算时间达到最大，且无法获得正确的识别结果。尽管加上这种情况时，识别率依旧保持在一个很高的水平。

5 结束语

通过利用软件无线电和神经网络，搭建了一套数据驱动的频谱监测识别系统，可以持续性获取某一固定频段的频谱数据，并在监测设备前端完成数据预处理。再通过PCA、归一化和BP神经网络，实现该频段频谱状态的识别分类，从而达到区域无线电环境的监测或智能干扰排查的目的。本系统主要依托于BP神经网络，频谱状态的识别率高达96%左右。目前此系统经过训练后能反应复杂的频谱现有状态，未来可根据指定的异常训练样本，对异常情况作出智能判定。本文完成的主要工作和创新点在于：

① 将GNURadio软件无线电平台和BP神经网络相结合，形成一套从频谱信息实时采集到分析识别处理的完整系统，解决了传统频谱监测系统持续性较差的缺陷。

② 对某一固定频段的频谱状态进行识别，而并非对单个调制信号进行识别。同时针对复杂不易训练的频谱波形创造了一种预处理算法。在本文的实验中，神经网络被训练以识别2.4 GHz公用频段的短时间内频谱状态，反映整个频段的信号数量和信号类型。

③ 根据采集到的频谱数据特点，制定了相应的神经网络识别方法。利用信号特征数据和PCA算法有效提高了神经网络的识别性能与效率。