一种基于物理层加密的OFDM系统设计与实现

孙艺夫，李 为，雷 菁

(国防科技大学 电子科学学院，湖南 长沙 410000)

0 引言

5G无线通信技术迅猛发展，正交频分复用技术(OFDM)也日益受到重视，其在抗多径码间串扰、多径衰落以及多普勒频移等难题上有着其他技术难以比拟的优势。但是，传统OFDM系统的安全传输问题也日益严重，当前主要依靠基于计算量的传统加密体制以保证安全性，而超级计算机的快速发展和量子计算机的出现，使其安全性受到严峻挑战。因此，兼具安全性、低复杂度、低功耗和低时延的物理层安全技术逐渐引起了研究者们的广泛关注，也积累了丰硕的理论知识与实践成果。当前的无线物理层安全传输技术研究主要分为2条主线展开[1]：以Wyner[2]为代表的基于信道窃听模型、无密钥的物理层安全传输技术，包括多天线波束成形技术[3-5]、人工噪声[6-9]、协同干扰技术[10-13]等；以Maurer[14]为代表的基于密钥的物理层安全传输技术。本文主要研究5G无线通信系统中基于密钥加密的物理层安全传输技术，提出在OFDM系统中使用物理层加密技术增强安全性，设计一种基于物理层加密的OFDM系统。

1 系统模型

本文主要考虑的系统结构如图1所示。将以前提出的一种基于等距变换的物理层加密(Physical Layer Encryption，PLE)[15]引入基于IEEE.802.11d标准的OFDM系统中，即在原OFDM系统的发送端调制之后引入基于密钥的物理层加密模块，对应合法接收端引入匹配的物理层解密模块，从而构建基于物理层加密的OFDM系统(PLE-OFDM)，以实现保密通信。其中核心模块-物理层加密模块框图如图2所示。

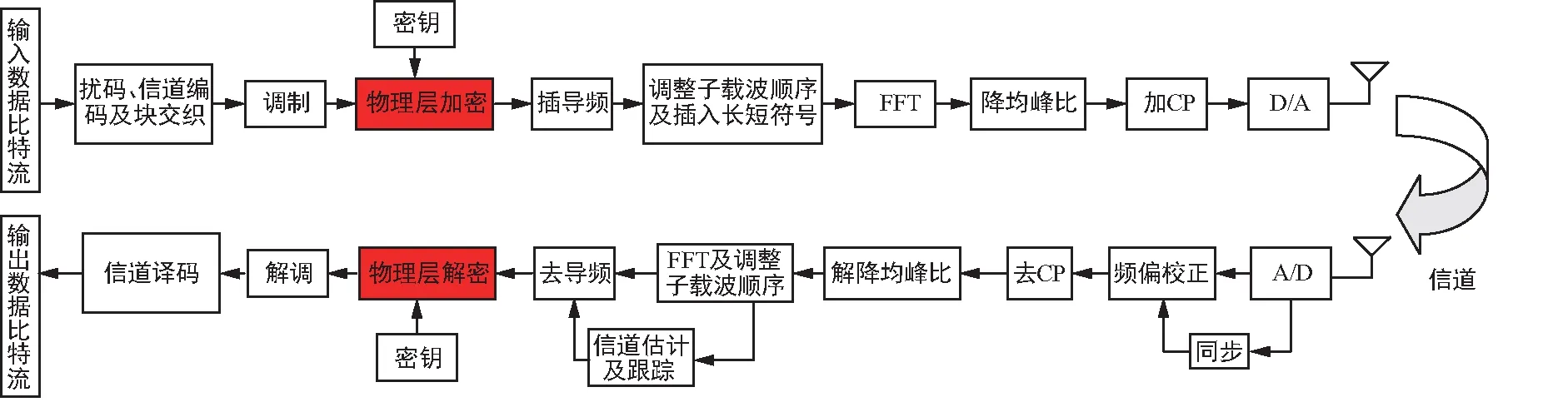
图1 PLE-OFDM系统结构框图Fig.1 System model of PLE-OFDM

图2 物理层加密模块框图Fig.2 Block diagram of physical layer encryption

物理层加密模块包含3个步骤：比特变换、调制及数据块变换。在物理层加密不同阶段采用不同的密钥，这些密钥是从原始密钥K派生而来的，将短主密钥K扩展为相对不同的扩展密钥(K1，K2，K3)，以便在加密算法中使用[16]。具体如下：

① 比特变换阶段：可以采用交织、置换、排列等布尔函数[17-18]。通过K1可以将二进制向量数据流S变成数据块S′。

② 调制阶段：采用 BPSK,QPSK,16QAM等常见调制方式，也可以设计新的多维调制方式，即：

式中，M为比特长度，N为星座符号数。

③ 数据块变换：作为最核心的部分，将调制复数序列X加密变换为密文信息Y，本质上是复数向量空间的映射函数设计，即：

X={X1,X2,…,XN}→Y={Y1,Y2,…,YN}。

在此使用等距变换作为映射变换函数，所谓等距变换，其定义如下：

设P和Q两个度量空间，其度量标准为dp和dQ。如果对任何a,b∈P都有一个映射f：P→Q，如果有：

dQ(f(a),f(b))=dP(a,b)，

则称之为等距变换。而等距变换在通信系统中不会改变平均解调误码率，相关证明如下：

假设等距变换后，原来信号S={S1,S2,…,SM}变成了Y={Y1,Y2,…,YM}，根据等距变换的定义，对任意i,j≤M，有

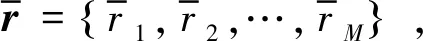
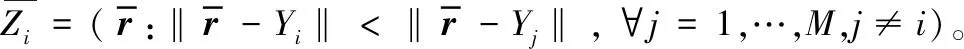
接收的Si和Yi的ML误码率可以表示为：

而在数学中，P和Q之间的所有等值面可以用N×N酉矩阵U来表示，即等距变换可以用酉矩阵来表示：

UUH=UHU=ΙN，

式中，(·)H为共轭转置，I为单位矩阵。

显然，|det (U)|=1，U矩阵的所有行和列向量都是标准正交基。事实上，任何N×N酉矩阵U都具有N2独立的实相参数。因此，可以根据密钥K给定的旋转方向Φ∈N，然后生成N×N的酉矩阵U，生成N×N酉矩阵的方法由文献[19]给出。

以N=2为例，2×2酉矩阵的一般表达式为：

其取决于4个参数Φ={φ,φ1,φ2,θ}，并且Φ={φ,φ1,φ2,θ}可以作为通信的密钥。还可以拓展U矩阵的维度去获取更强的安全性。综上所述，基于等距变换生成酉矩阵U，并且可以用一个密钥生成多个酉矩阵，对每个符号使用不同的酉矩阵，增加其随机性，实现复数域上的“一次一密”。综上所述，数据块变换可表示为：

Yn=XnU，

其中，U为等距变换的酉矩阵。而对应的解密模块可以推导为：

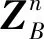
2 仿真实现与分析

本节使用Matlab对基于物理层加密的OFDM系统进行仿真实现。由于本文是对物理层加密和OFDM系统的结合，故要从物理层加密的可行性和安全性角度来进行仿真分析。物理层加密的可行性，即加入物理层加密后对原来OFDM系统除安全性以外的其他指标不会降低，且复杂度与时延较已有的物理层安全算法有着明显的降低；而安全性即提升了原始OFDM系统的安全性。

2.1 可行性分析

2.1.1 误码率

对不同信道及调制方式下，PLE是否对误码率性能有影响进行仿真，仿真结果如图3所示。从图中分析可得，在瑞利信道与多径信道下，无论哪一种调制方式，PLE并不影响OFDM的误码率指标与对抗多径性能，可行性得到验证。

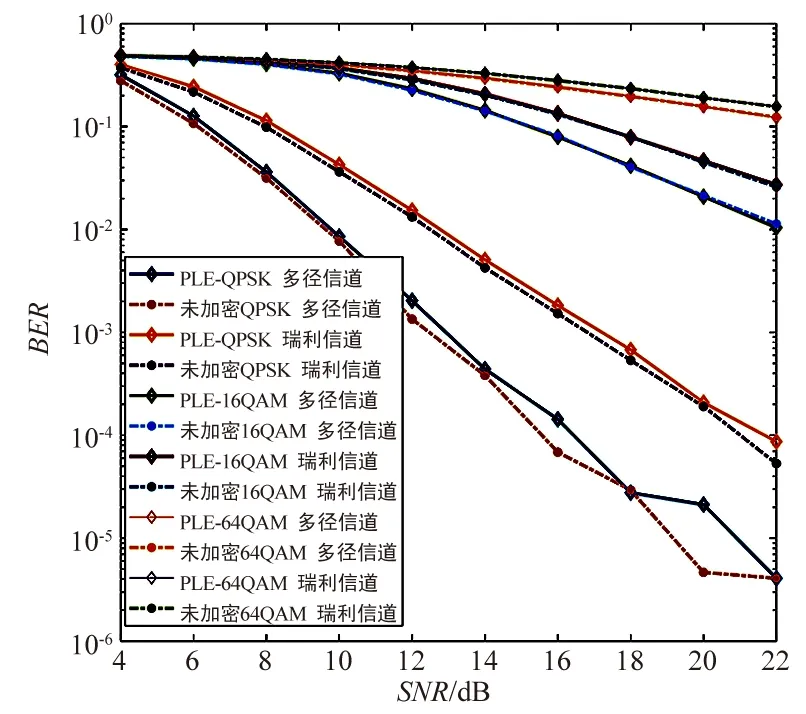
图3 不同信道及调制方式下误码率随信噪比变化图Fig.3 BER-SNR under different channels and modulation modes

2.1.2 复杂度与时延

该系统的运算主要包括两部分：安全矩阵的生成与数据块变换。安全矩阵的生成过程是非实时的,不需要每次传输数据时都运行。而数据块变换为实时加密模块，需要每次传输数据时都运行。所以系统的运算复杂度和时延主要由数据块变换模块产生。数据块变换算法的复杂度为分别在发送端和接收端增加了1个N2的复数矩阵乘法。而已有的较低复杂度的算法为O(N2.37)，此处的N不是数据长度而是块的大小，在实际系统中N取值并不大，可以取4或8，所以本系统的复杂度并不高，能够降低当前物理层加密通信系统复杂度和时延。实际上已经有很多成熟的矩阵乘法的硬件实现方案，具有较低复杂度和延时，故所研究的系统很容易硬件实现，故有很高的可行性。

2.2 安全性分析

加入PLE到现有的OFDM系统中，其最主要目标就是提升其安全性，而安全性可从理论及仿真结果分析，接下来从两方面对其安全性进行分析。

2.2.1 理论分析

仅密文攻击：由于采用密码学基础中的各种公私钥对算法生成公私钥，其中数学问题难以解决。并且密钥通过物理层加密算法转换后变成复数空间，其空间大小几乎是无穷的，可以防止暴力破解，所以足够大的密钥长度即可保证安全性。

已知明文攻击和选择性明文攻击：针对已知明文和选择性明文攻击，考虑在加性高斯白噪声信道情况下，窃听者接收信号为：

ZE=U(X)+nE。

式中，ZE为窃听者接收到的信号，由于U(X)加入了随机性，并且窃听者窃听到的信号叠加了噪声nE，即使X不变，在不同时刻得到的ZE也不同，所以即使已知X,也无法得到变换函数U(·)对应的密钥K。故可以对抗已知明文攻击。

由于酉矩阵具有N2个矩阵元素，即使针对方程Yn×1=Un×nXn×1窃听者也无法通过已知Y和X求解出U。而且对于不同信息符号，加密酉矩阵U会发生变化，窃听者也无法通过累积一定量Y和X来分析求出U，所以可以对抗选择性明文攻击。

2.2.2 仿真结果分析

通过图4对比可以发现，16QAM调制通过物理层加密后，将原始信息的星座图的幅度和相位特征完全改变，星座图被混淆，近似为噪声信号。而在接收端，由于信道中的噪声影响，星座图被进一步混淆，形成一个比原来加密后的星座图更加集中的星座图。在接收到加密的信号后，窃听者仍不能恢复信息，星座图仍然是一个接近噪声的信号，而合法通信方可以使用解密算法进行正确解密。

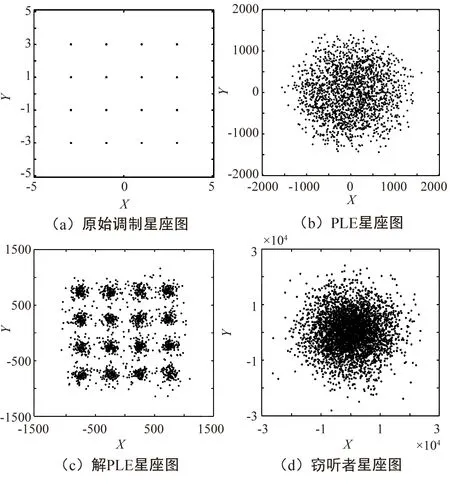
图4 16QAM-PLE-OFDM系统各阶段星座图对比Fig.4 Comparison of constellation diagrams atvarious stages of 16QAM-PLE-OFDM

为了衡量混淆程度以量化安全性程度，引入联合星座熵,其定义为：

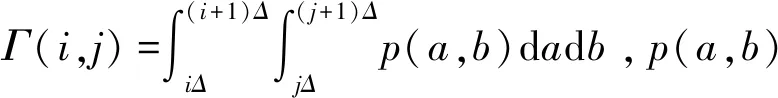
星座熵仿真如图5所示，可见星座熵随星座坐标量化长度的增加而增加，将本文研究的PLE方法引入OFDM系统，较以往方法星座图的混淆度有显著提升，安全性提升程度更高。并且还可以看到调制方式的改变会使得星座图混淆度改变，这是因为欧氏距离和星座图点数所导致的。原来的QPSK每个星座点的欧式距离大于16QAM，每个星座点的欧式距离和QPSK点数少于16QAM。显然根据熵的定义，16QAM的混乱度更高，即安全性更高，不过这会以牺牲误码率为代价。 结果表明，在OFDM系统中加入PLE可以显著提高星座的星座熵，意味着PLE-OFDM可以使星座高度混乱并且星座信息的泄漏较少。

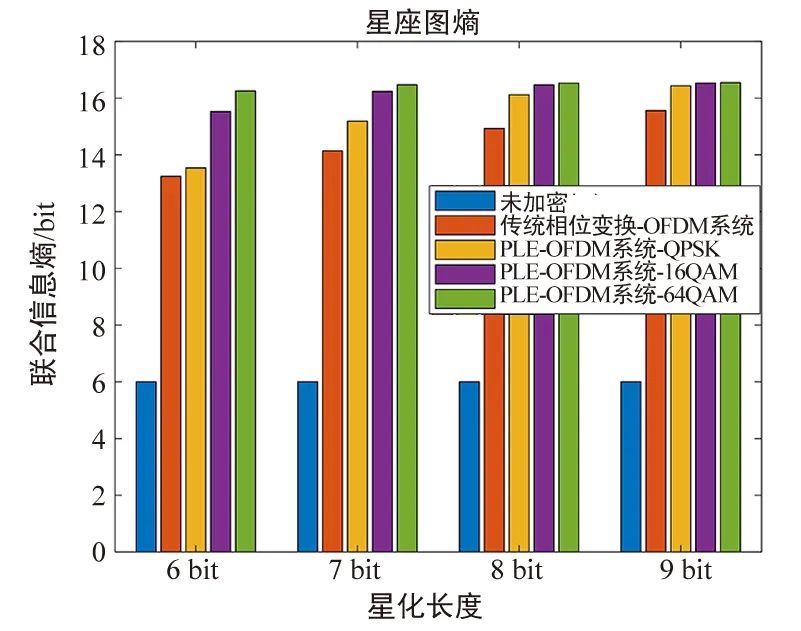
图5 星座熵Fig.5 Constellation entropy

综上所述，PLE几乎不会影响各个参数的设定、作用及规律，所以它相当于独立于其他模块存在。并且在各种仿真中，都可以看到PLE并不影响整个系统在各种信道下的误码率等通信指标，并且PLE后的星座图基本近似成噪声，混淆程度比较高，合法者可以通过解密恢复信息，窃听者却无法解密信息，安全性有着显著提升。同时，物理层加密技术可以实现低延时、低功耗等要求，故PLE-OFDM可行性很高。

3 结束语

针对当前5G无线通信系统中的安全问题，从物理层角度出发，提出了一种基于等距变换的物理层加密的OFDM系统，该系统通过利用密钥对调制后的复数序列进行等距变换，得以实现物理层加密。仿真结果表明，该系统兼具OFDM系统抗多径效应与物理层安全性能，且复杂度与时延较现有的物理层安全系统均有下降，未来可大规模应用于无线通信系统。