考虑尺寸影响的箍筋约束混凝土轴压本构模型

金浏，李平，杜修力

(北京工业大学 城市减灾与防灾防护教育部重点实验室，北京 100124)

约束混凝土力学性能的研究表明，箍筋的约束作用能够显著改善混凝土的强度和延性。学者们对箍筋约束混凝土柱轴心受压性能开展了大量研究，并提出了考虑箍筋间距、箍筋形式及混凝土强度等多种参数影响的本构模型。Kent等[1]提出的应力-应变曲线的上升段采用分数方程，下降部分采用线性函数表示。Saatcioglu等[2]提出的应力-应变模型包括抛物线形式的上升段，线性下降段和等于20%峰值强度的残余强度。Mander等[3]、Razvi等[4]、Chung等[5]、赵作周等[6]、史庆轩等[7]也分别提出了不同的约束混凝土本构模型。然而，上述箍筋约束混凝土应力-应变关系模型多针对试件尺寸小于工程中实际应用的构件，难以考虑试件尺寸对混凝土力学性能的影响。

在证实混凝土材料存在尺寸效应的基础上[8-12]，研究者也对箍筋约束混凝土构件的轴心受压性能进行了试验研究[13-17]，结果表明：箍筋约束混凝土的轴压强度存在明显的尺寸效应，且随约束作用的增强而减弱。另外，Kim等[13]基于试验提出了箍筋约束混凝土尺寸效应公式，并且得出尺寸效应的强弱受体积配箍率的影响，即随着体积配箍率的增加而逐渐减弱，当体积配箍率达到某一临界值时，混凝土尺寸效应将消失。Du等[17]也得出了相同的研究结论，他们还研究了不同箍筋形式下约束混凝土抗压强度的尺寸效应，结果表明：由于圆形箍筋约束作用较方形箍筋强，圆形箍筋约束混凝土柱的尺寸效应较弱。实际上，一些传统的本构模型对尺寸效应已有考虑，如Park等[18]和Legeron等[19]的工作，采用强度折减系数(如取值为0.85)的方式来考虑试件尺寸的影响。这是一种粗糙的处理方法，不能科学地体现构件的承载力、变形能力随尺寸变化而产生的非线性变化特性。宋佳等[20]在Kim等[21]提出的峰值应力(强度)尺寸效应公式基础上，建立了可考虑尺寸影响的箍筋约束混凝土轴压本构关系模型。尽管如此，Kim等[20]的强度模型不能描述箍筋约束作用对约束混凝土柱轴压强度尺寸效应的定量影响。

近年来，Jin等[22]结合材料层次经典的尺寸效应律及箍筋约束作用机制，建立了约束混凝土柱轴压强度(峰值应力)的半经验-半理论公式。笔者在该研究工作的基础上，进一步考虑试件尺寸、体积配箍率、箍筋形式对箍筋约束混凝土峰值压缩应变的定量影响，并建立考虑尺寸影响的箍筋约束混凝土峰值应变的计算公式。进而，结合峰值应力(强度)和峰值应变计算公式，建立能考虑尺寸影响的箍筋约束混凝土轴压应力-应变关系模型。与现有的考虑尺寸效应的箍筋约束混凝土本构模型相比，模型中峰值应力公式的力学机理清晰，能够定量地描述箍筋率以及结构尺寸对峰值应力及峰值应变的影响。

1 箍筋约束混凝土的受压性能及尺寸效应分析

1.1 箍筋约束混凝土轴压力学性能

文献[22-23]在箍筋约束混凝土轴压破坏试验[17,24]的基础上，深入开展了三维细观数值模拟与研究，考虑了试件尺寸、体积配箍率及箍筋约束形式的影响，分析了箍筋约束混凝土柱轴压破坏力学性能及尺寸效应规律，最终建立了能反映箍筋率定量影响的约束混凝土轴压强度尺寸效应半理论-半经验公式。表1为箍筋约束混凝土圆柱[22]及方柱[23]的试件几何参数及部分模拟结果。试件编号如Y-0-S、F-0-S中，首字母为箍筋约束形式，“Y”代表圆形，“F”代表方形；0为体积配箍率；“S”、“M”、“L”、“U”分别表示小、中、大、特大4种尺寸，圆柱及方柱的模型尺寸见表1。试件详细设计参数见文献[22-23]。其中，混凝土试件的峰值应力σcc定义为

(1)

式中：Pu、As、Ac分别为峰值荷载、纵筋截面面积及混凝土截面面积。

1.2 应力-应变曲线影响因素

1.2.1 试件尺寸 图1为文献[22-23]模拟获得的具有相同体积配箍率、不同试件尺寸的圆形及方形箍筋约束混凝土柱应力-应变曲线。图1中，方形截面柱所采用的材料参数(骨料、砂浆及界面过渡区等细观组分的本构模型力学参数，详见文献[22-23])比圆柱大，所以，方柱的峰值强度比圆柱高。由图1可知，不同尺寸试件的曲线上升段几乎重合，初始切线模量基本一致，然而峰值应力、峰值应变以及峰值后软化曲线有较大差别。随着试件尺寸增大，约束混凝土柱的峰值应力显著降低，峰值应变也有所减小，但变化不明显。同时，随着试件尺寸增大，箍筋对混凝土的约束作用减弱，混凝土试件破坏脆性增强，应力-应变曲线下降段越来越陡。

表1 试件几何参数及模拟结果

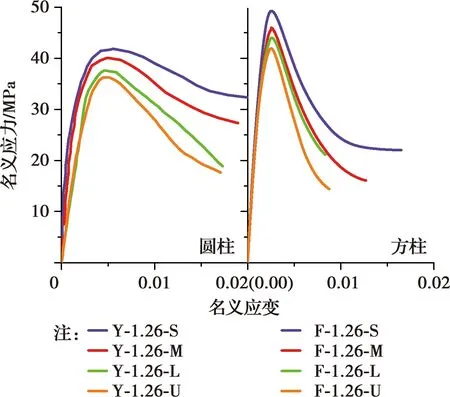
图1 试件尺寸对应力-应变曲线的影响

1.2.2 体积配箍率 图2为文献[22-23]模拟获得的圆形及方形箍筋约束混凝土柱在相同尺寸不同配箍率下的应力-应变曲线。从图2中可以看出，随体积配箍率的增大，约束混凝土的峰值应力增大，下降段的坡度变缓，试件破坏时延性有所提高。这是因为体积配箍率的增大，箍筋对混凝土的约束作用增强，混凝土的脆性程度降低。

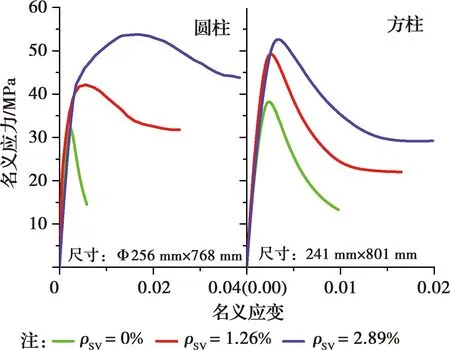
图2 配箍率对应力-应变曲线的影响

1.2.3 箍筋约束形式 由图2中的曲线可知，箍筋约束形式对约束混凝土的应力-应变曲线有显著影响。两种曲线的区别主要体现在峰值点附近以及曲线的下降段。圆形箍筋约束混凝土柱的峰值点附近曲线比方形箍筋约束试件更加圆滑，没有明显的尖峰。另外，圆形箍筋约束混凝土柱的应力-应变曲线下降段较平缓。这是因为方形箍筋在四个角部处的约束力较大，截面边长中部的箍筋约束力小，对混凝土的约束不均匀，而圆形箍筋对混凝土的约束力分布均匀，约束作用较强。

2 考虑尺寸影响的峰值应力和峰值应变

2.1 峰值应力

文献[22-23]分别基于圆形和方形箍筋约束混凝土柱轴心受压试验，结合三维细观数值模拟分析，探讨了箍筋的约束作用对混凝土柱轴压破坏及尺寸效应的影响机制。归纳总结出箍筋的约束作用一方面可以提高混凝土的强度，另一方面可以削弱混凝土的尺寸效应，这两方面的作用分别由强度提高系数φ和尺寸效应削弱系数β来表征。

此外，文献[22-23]基于Bažant材料层次尺寸效应律，提出了可反映箍筋约束作用的钢筋混凝土柱轴压破坏峰值应力(强度)尺寸效应公式，见式(2)。

(2)

式中：对于圆柱，fc为Φ150 mm × 300 mm混凝土圆柱体试件的轴心抗压强度，对于方柱fc取150 mm× 150 mm×300 mm混凝土棱柱体试件的轴压强度；B、D0为依赖于结构的几何常数，通过对不同尺寸素混凝土试件的抗压强度模拟值进行回归分析得到，对于圆柱B=1.017、D0=800，对于方柱，B=1.176，D0=714；D为试件尺寸(圆柱为截面直径，方柱为截面边长)；φ为箍筋对混凝土强度的提高作用，β为箍筋对混凝土尺寸效应的削弱作用。由于约束机理不同，方形及圆形箍筋对核心混凝土的约束应力分布存在较大区别，式(2)中φ和β的确定也有所不同。

2.1.1 强度提高系数φMander等[3]考虑体积配箍率、箍筋形式、箍筋间距等因素建立了箍筋约束混凝土的应力-应变关系模型。模型中包含的核心混凝土峰值强度的计算方法常被后人借鉴，如Mirmiran等[25]、Fam等[26]在研究FRP约束混凝土时采用了该方法。该模型用有效约束系数ke来表征箍筋的有效约束力，ke为横截面有效约束面积与混凝土核心区面积的比值。

对于圆形截面，根据Mander等[3]的理论研究可知，约束混凝土柱强度提高系数为

式中：fc为混凝土的轴心抗压强度；fl为箍筋对混凝土的侧向压应力；fl/fc表示约束应力比；fyh为箍筋的屈服强度；s′为相邻箍筋净距；ρcc为核心区纵筋配筋率；ds为箍筋中心线包围的截面直径。

对于方形截面，强度提高系数可通过图3查得。其中，箍筋对核心混凝土区域的有效侧向约束力计算公式为

(6)

(7)

式中：c为边缘箍筋中心间距；As为箍筋各肢在柱边长方向投影面积之和；wi为第i个相邻纵筋的净距。对于方形截面柱，分别计算截面x、y方向上的有效侧向压应力，fl1、fl2分别为方形截面x、y两个方向有效侧向约束力的较小值和较大值，强度提高系数可通过图3查得。

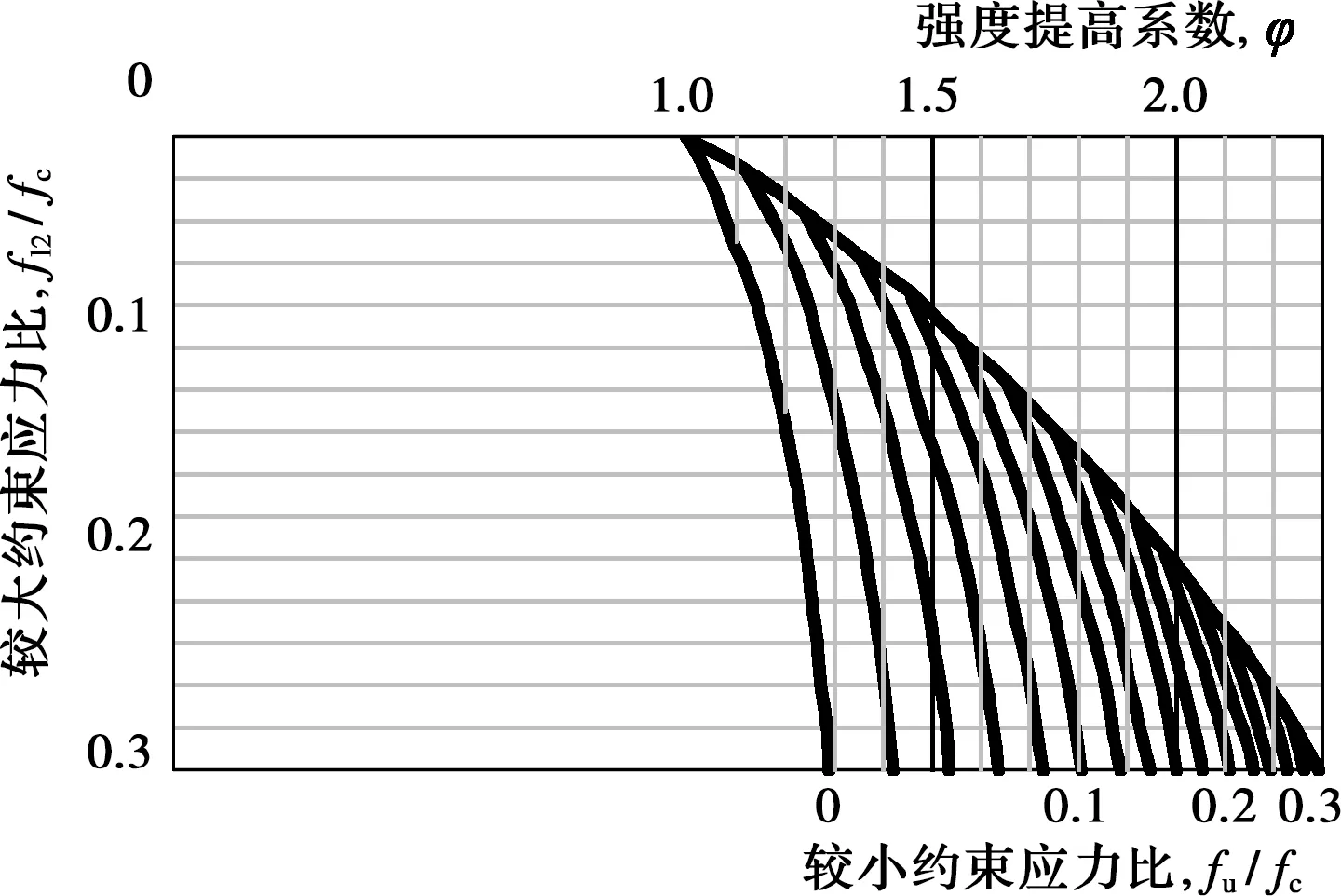
图3 方形箍筋约束混凝土强度提高系数的确定

2.1.2 尺寸效应削弱系数β由于箍筋的约束作用，柱的延性能力增强，脆性程度降低，约束混凝土柱的尺寸效应逐渐削弱，该行为可用尺寸效应削弱系数β来表示。当箍筋率很小时，箍筋的存在对柱轴压破坏尺寸效应无影响，此时β=1；箍筋率ρsv越大，强度尺寸效应的削弱作用越显著，削弱系数β越大。

图4给出了削弱系数β随配箍率ρsv变化的近似关系曲线，图中3条曲线表示β随ρsv变化的快慢，且曲线上限和下限具有明确的物理意义和力学意义。尺寸效应削弱系数β表达式为

(8)

式中：α为调节系数，反映削弱系数β随箍筋率变化的快慢。根据《混凝土结构设计规范》(GB 50010—2010)[27]，体积配箍率下限值ρsv,min建议取为0.25%。对于圆形箍筋约束混凝土柱，α建议取值为8.0；对于方形箍筋约束试件，α建议的值取为1.0。具体确定方法详见文献[22-23]。

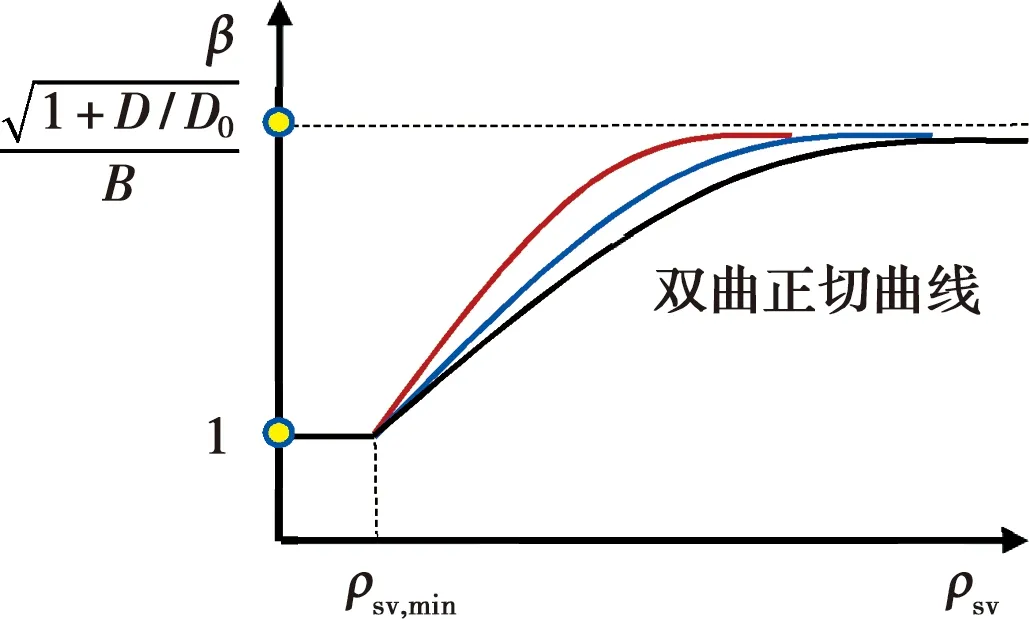
图4 尺寸效应削弱系数β的确定

2.1.3 峰值应力公式的验证 为了验证所提出的箍筋约束混凝土峰值应力尺寸效应计算公式的准确性，选取了文献[16,28-30]中15根圆形箍筋约束混凝土柱试件和36根方形箍筋约束混凝土柱试件，对试验数据进行了整理，如表2所示。统计试件的截面尺寸范围为200～600 mm，抗压强度范围为25～51 MPa，配箍率范围为0.6%～4.5%。图5分析了搜集的Mander等[28]、Li等[16]、钱稼茹等[29]、胡海涛等[30]的试验峰值应力值与本文公式计算值的对比情况，可以看出，峰值应力公式能较好地预测约束混凝土的峰值应力。此外，关于圆形箍筋约束混凝土柱的轴压试验较少，已有的试验数据显示峰值应力的计算值略显保守。总体来说，所提出的峰值应力计算公式具有较高的精确度。

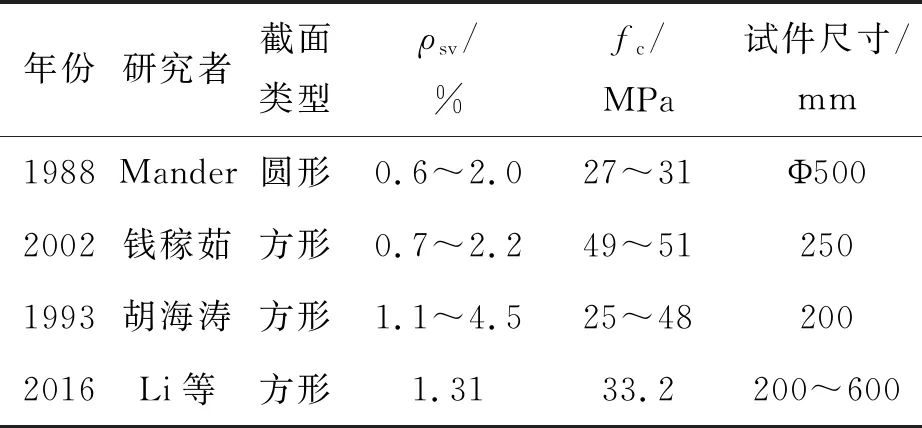
表2 箍筋约束混凝土柱轴压试验数据Table 2 Test data of stirrups-confined RC columns under axial compression

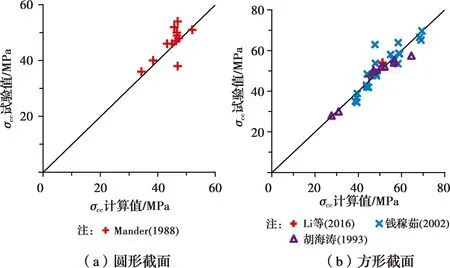
图5 峰值应力公式计算值与其他试验值对比

2.2 峰值应变

箍筋约束混凝土柱试件在轴心受压破坏时，除峰值应力存在尺寸效应外，对应的峰值应变也在一定程度上受试件尺寸的影响，其尺寸效应问题不容忽视。然而，目前约束混凝土尺寸效应的研究主要集中于峰值应力，约束混凝土的峰值应变尺寸效应的研究相对较少。因此，关于箍筋约束混凝土的峰值应变尺寸效应的研究，缺少相关的试验数据及理论分析模型。

鉴于无法通过理论分析得到峰值应变的尺寸效应规律，考虑约束比(fl/fc)和试件尺寸的影响，采用非线性最小二乘法对文献[22-23]模拟结果进行回归分析，得到圆形箍筋约束混凝土和方形箍筋约束混凝土的峰值应变计算公式。

圆形箍筋约束混凝土柱

(9)

方形箍筋约束混凝土柱

(10)

式中：εco为非约束混凝土的峰值应变，取为0.002；fl为侧向压应力，圆形箍筋混凝土试件通过式(4)和式(5)计算，方形箍筋混凝土试件根据式(6)和式(7)计算。

从式(9)和式(10)中可以看出，约束混凝土的峰值应变与试件尺寸成反比，即随着试件尺寸的增大，峰值应变逐渐减小，这与试验结果一致。此外，还可以看出，随着约束比的增大，峰值应变也增大，即混凝土变形能力增强。

图6为式(9)和式(10)计算值与文献[22-23]中部分箍筋约束混凝土试验及模拟结果的对比。从图6可以看出，当体积配箍率相同时，随着截面尺寸的增大，试件的峰值应变逐渐变小，箍筋约束混凝土柱的峰值应变存在明显的尺寸效应。总的来说，式(9)和式(10)能够较好的预测文献[22-23]中约束混凝土试件的峰值应变尺寸效应规律。

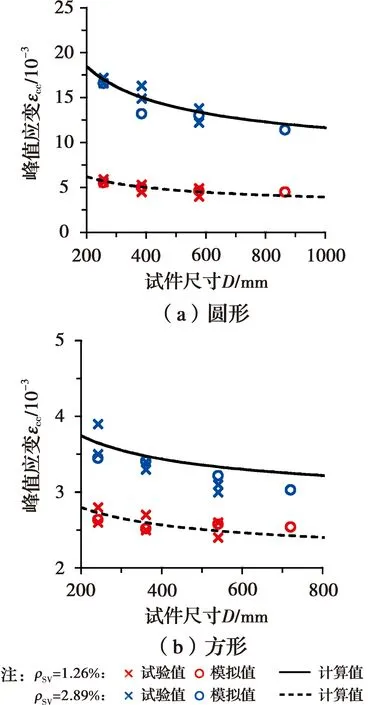
图6 峰值应变计算值与文献[22-23]试验及模拟值对比

另外，图7分析了箍筋约束混凝土峰值应变公式计算值与文献[16,28-30]中试验结果的对比情况。由图7可见，大部分峰值应变的计算值与文献中试验值拟合较好，圆柱峰值应变计算值与试验值之比的平均值为0.94，变异系数为0.15；方柱峰值应变计算值与试验值之比的平均值为0.93，变异系数为0.20。由于应变测量的敏感性，相较于峰值应力，峰值应变试验结果具有较大的离散性。

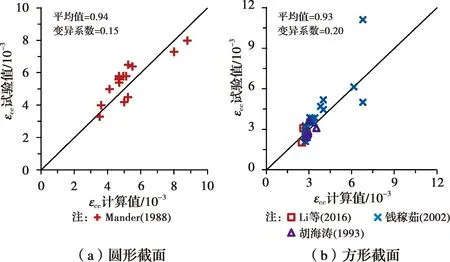
图7 峰值应变公式计算值与其他试验值[16,28-30]对比

3 箍筋约束混凝土轴心受压本构模型

在箍筋约束混凝土柱轴压试验及模拟结果的基础上，通过考虑尺寸对约束混凝土峰值应力和峰值应变的影响，提出考虑尺寸影响的箍筋约束混凝土轴压本构模型。

3.1 上升段

Hsu等[31]、Cusson等[32]以及Hoshikuma等[33]建立的箍筋约束混凝土应力-应变模型均采用Popovics[34]方程形式，Mander[3]约束混凝土应力-应变模型也采用了该方程，该公式预测准确度高，应用性较好，因此，上升段采用式(11)表示。

(11)

式中：σcc和εcc分别为约束混凝土峰值应力及峰值应变；r为混凝土脆性相关系数，表达式为

式中：Ec为混凝土的初始弹性模量，N/mm2。

3.2 下降段

在《混凝土结构设计规范》[27]素混凝土本构模型基础上，考虑箍筋的约束作用对曲线下降段趋势的影响，根据试验及模拟结果对混凝土应力-应变曲线下降段的相关参数进行了调整，下降段曲线的表达式为

3.3 计算步骤

根据提出的峰值应力、峰值应变尺寸效应计算公式，建立考虑尺寸影响的箍筋约束混凝土应力-应变关系模型，主要计算步骤如下：

1)指定箍筋约束混凝土柱的初始应变εi；

2)采用式(2)～(5)、式(8)或式(2)、式(6)～式(8)计算出约束混凝土圆柱或方柱的峰值应力σcc；

3)采用式(9)或式(10)计算出约束混凝土圆柱或方柱的峰值应变εcc；

4)当εi≤εcc时，由式(11)～式(13)计算得到应力-应变曲线上一点；

5)不断增大εi，重复步骤(4)，当εi>εcc时，由式(14)～式(16)计算得到应力-应变曲线上一点。

3.4 模型验证

采用本文模型计算箍筋约束混凝土的应力-应变曲线，并与文献[17,22-23]中部分试验及模拟曲线进行了比较，如图8、图9所示。从图8、图9可以看出，不论是箍筋约束混凝土圆柱还是方柱，建议的应力-应变模型与试验及模拟曲线吻合较好，能够反映不同设计参数的箍筋约束混凝土柱的应力-应变规律。另外，从图8(c)、(d)及图9(c)、(d)可以看出，本文理论模型曲线的软化下降段与试验曲线还存在差异，这是由于未考虑约束混凝土极限应变及破坏应变的影响所造成的。

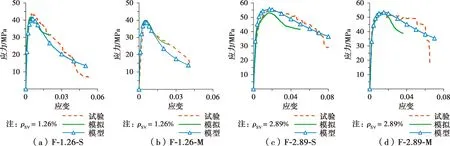
图8 模型计算曲线与圆柱试验[17]及模拟[22]曲线的对比

图9 模型计算曲线与方柱试验[24]及模拟[23]曲线的对比

图10中同时给出了本文模型对文献[22]中试件的预测曲线与Mander模型预测曲线(未考虑尺寸的影响)，可知:本文模型考虑了尺寸的影响，不同尺寸试件的峰值应力和峰值应变有较大差别。试件尺寸较小时，本文模型与Mander模型相差较小，但随着试件尺寸的增大，考虑尺寸影响的模型与传统本构模型差别愈发显著。总体来说，考虑尺寸影响的轴压本构模型能够更加准确地预测大尺寸约束混凝土试件的轴压性能，而未考虑尺寸影响的应力-应变模型高估了大尺寸试件的峰值应力和峰值应变，这大大降低了工程设计的可靠度。

图10 模型计算曲线与Mander模型[3]的对比

4 结论

在前期研究的基础上，分析箍筋约束混凝土柱轴心受压应力-应变曲线的影响因素，提出了考虑尺寸影响的箍筋约束混凝土本构关系模型，主要结论如下：

1)试件尺寸是箍筋约束混凝土柱轴压力学性能的重要影响因素，随着试件尺寸的增大，峰值应力和峰值应变均有减小的趋势，在建立箍筋约束混凝土本构关系时应考虑试件尺寸的影响。

2)对箍筋约束混凝土轴压试验中峰值应变数据进行回归分析，提出了约束混凝土的峰值应变计算公式，该公式能够较好地描述试件尺寸及约束比对峰值应变的影响。

3)建立了考虑尺寸影响的箍筋约束混凝土本构关系模型，该模型与试验及模拟曲线吻合较好，能够较准确地反映大尺寸试件的应力-应变关系。

本文仅探讨了箍筋率、箍筋形式(方形箍筋及圆形箍筋)和试件尺寸对约束混凝土轴压力学性能的影响，尚未考虑箍筋间距、混凝土强度及长细比等因素的影响，后续仍需对此进行深入的分析。若要提出具有更广泛适用性的计算方法，尚需根据更多参数的试验数据调整已有模型。