基于邻域粗糙集组合度量的混合数据属性约简算法
盛 魁 卞显福 董 辉 马 健
1(亳州职业技术学院信息工程系 安徽 亳州 236800)2(中国科学技术大学软件学院 安徽 合肥 230051)
0 引 言
属性约简[1]是一种重要的数据挖掘方法,它通过对样本数据中的属性进行选择,从而达到了知识发现的效果,同时它也是一种有效的数据维度约简工具,有助于提高机器学习等相关算法的学习性能,是目前数据分析领域的一个研究热点。
属性约简是粗糙集理论的一个重要应用。目前的属性约简已经适用于离散型[2]、连续型[3-4]以及混合类型的信息系统[5],其中基于混合信息系统的属性约简算法通过邻域粗糙集模型进行实现。Hu等[5]学者通过邻域依赖度在混合信息系统中构造属性约简算法。Zhao等[6]通过条件熵在混合不完备信息系统构造属性约简算法。Zhang等[7]利用模糊熵也构造出了相应的属性约简算法。因此,目前基于混合信息系统的属性约简方法逐渐受到学者们的广泛关注。
然而,Liang等[8]指出,传统的属性约简通过单一的度量方法不能够得到更好的属性约简结果,通过多个方法共同评估属性可以提高属性约简算法的性能,因此近年来也提出了一些组合度量的属性约简方法[9-10],在这些方法中,很少有对混合信息系统的属性约简进行相关研究,这促使我们在混合信息系统构造出基于组合度量的属性约简算法。
邻域依赖度是混合信息系统属性约简中一种常用的启发式函数[5,11],知识粒度是描述属性对信息系统粒化能力的一种常用度量[12]。因此,本文将知识粒度在混合信息系统中进行推广,提出邻域知识粒度,然后将邻域依赖度与邻域知识粒度进行结合提出邻域组合度量,并将该度量方法作为启发式函数来构造属性约简,最后通过一系列实验来验证该算法的性能。
1 基本理论
混合数据是一种复杂的数据类型,通常是由离散型和连续型数据共同构成的数据集,在属性约简的研究中,混合数据被定义为混合信息系统的形式,混合信息系统可表示为IS=(U,A),其中U为对象集,即该数据集的样本空间,每个样本称之为对象,A为属性集,即该数据集的特征集,若属性集A=C∪D,且C∩D=∅,其中,D为数据集的类标记特征属性,那么此信息又被称为决策信息系统,C、D分别称为条件属性和决策属性。
在混合信息系统中,邻域粗糙集模型是一种常用的处理模型,即通过构造邻域关系来进行模型计算。
定义1[5]设混合信息系统IS=(U,A),属性集B⊆A,那么B在样本空间U上确定的δ邻域关系为:
(1)
这里的δ称为邻域半径,ΔB(x,y)为广义的距离度量函数,即对于B={a1,a2,…,am},广义距离度量ΔB(x,y)可表示为:
(2)
当属性ai为离散型属性时:
(3)
当属性ai为连续型属性时:
(4)
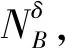
(5)
性质1[5]对于混合信息系统IS=(U,A),若P⊆Q⊆A且0≤δ1≤δ2,那么:
对象的邻域类相当于该对象在样本空间中给定邻域半径下的相近样本集。图1为对象邻域类的示意图。
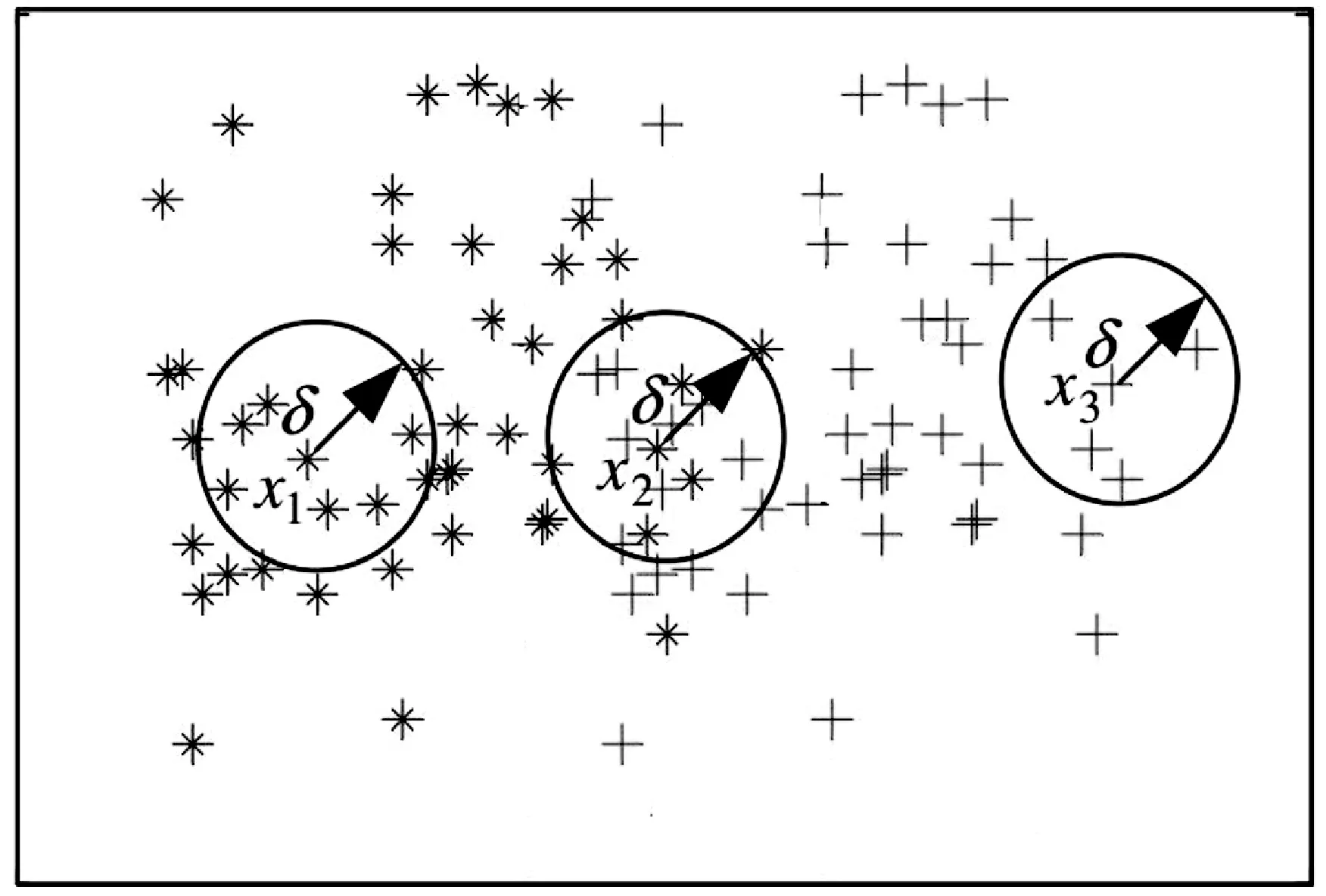
图1 对象的邻域类示意图
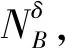
(6)
(7)
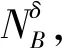
(8)
邻域依赖度满足0≤γB(D)≤1。
邻域依赖度反映的是混合信息系统中决策类下近似样本占据所有样本的比例,也是描述条件属性集和决策属性之间关系程度的一种度量,因此该度量可作为一种启发式函数来进行混合信息系统的属性约简。
2 混合信息系统的邻域组合度量方法
在文献[5]中,学者们通过邻域依赖度提出了相应的属性约简算法,均能够对混合信息系统进行有效的维度约简。Liang等[8]提出,通过单一的度量方法不能够达到较好的属性集评估效果,尤其是对于依赖度度量,结合其他视角的度量方法可以进行更优的属性约简。
Liang等[8]通过将传统的依赖度和粒计算视角下的知识粒度进行结合,提出一种新的粒度属性集评估方法,并通过实验验证了该方法的优越性。本节将这种方法推广到混合信息系统下,提出一种新的组合度量方法。
在提出组合度量方法之前,首先将粒计算模型中传统知识粒度在混合信息系统中的邻域关系下进行改进与推广,提出邻域知识粒度。
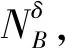
(9)
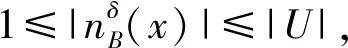
邻域知识粒度表示的是邻域关系对样本空间中每个对象的粒化能力的一种评估,邻域知识粒度越大,表明样本空间中每个对象的邻域类越小,说明该属性集对样本空间的粒化能力越强。

NGKδ2(B)≤NGKδ1(B)
(10)
证明当邻域半径满足0≤δ1≤δ2时,根据定义1中邻域关系的定义,对于∀x,y∈U,若ΔB(x,y)≤δ1必有ΔB(x,y)≤δ2。因此:
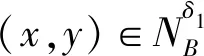
进一步:
即NGKδ2(B)≤NGKδ1(B)。

NGK(P)≤NGK(Q)
(11)
证明当属性集满足P⊆Q⊆A时,根据定义1中邻域关系的定义,对于∀x,y∈U,若ΔQ(x,y)≤δ则ΔP(x,y)≤δ。因此:
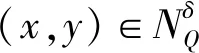
进一步:
即NGK(P)≤NGK(Q)。
在邻域知识粒度的基础上可以将邻域依赖度和邻域知识粒度进行结合,提出混合信息系统下的邻域组合度量方法。
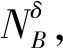
NMMB(D)=γB(D)·NGK(B)
(12)

NMMP(D)≤NMMQ(D)
(13)
证明根据文献[5],当属性集满足P⊆Q⊆A,那么邻域依赖度有:
γP(D)≤γQ(D)
同时根据性质3,有NGK(P)≤NGK(Q),因此可以得出NMMP(D)≤NMMQ(D)。
性质4表明,随着属性的逐渐增加,其邻域组合度量也是逐渐增加的,这满足了属性约简中度量函数的一个很重要的条件,因此根据邻域组合度量作为启发式函数,可以构造出混合信息系统的属性约简算法。
3 启发式属性约简算法
信息系统的属性约简是粗糙集理论在数据挖掘领域中的重要应用,是降低复杂数据维度的一种重要方法,本节将第2节中提出的邻域组合度量作为启发式函数,提出一种混合信息系统的启发式属性约简算法。
定义7对于混合决策信息系统IS=(U,C∪D),若属性集B⊆C是整个条件属性集C的属性约简,那么必须同时满足:
NMMB(D)=NMMC(D)
(14)
∀b∈B,NMMB-{b}(D) (15) 定义7表示的是基于邻域组合度量属性约简算法的定义,其中:式(14)表明最终属性约简结果必须和整个属性全集保持一致的邻域组合度量结果;式(15)表明这个属性约简结果不能再包含其他冗余的属性,即对属性约简集中剔除任意一个属性,式(14)都不成立,因此式(15)保证了最终约简结果是最精简的。 根据定义7中关于邻域组合度量属性约简的定义,本文按照一般启发式属性约简的构造方法,提出本文的属性约简算法。 算法1混合信息系统的邻域组合度量启发式属性约简。 输入:混合信息系统IS=(U,C∪D),邻域半径δ。 输出:属性约简结果red,其中red⊆C。 1. 初始化red=∅,NMMred(D)=1; 2. for ∀ai∈C-reddo 3. 计算 sai=NMMred∪{ai}(D)-NMMred(D); 4. end for 8. 返回Step2; 9. else 10. returnred; 为了验证本文所提出的邻域组合度量启发式属性约简算法具有更优的性能,本节将通过实验来比较分析,相关的实验主要包括两个方面,分别为比较算法的属性约简效率和比较算法的约简结果性能。 实验所运用的数据集如表1所示,这些数据集全部来自于UCI数据集,每个数据集都为包含离散型属性和连续型属性的混合类型数据。本实验进行比较的算法分别为:(1) 基于邻域依赖度的混合信息系统属性约简[5];(2) 基于最大决策的邻域粗糙集属性约简[13];(3) 基于邻域区分度的属性约简[14]。所有算法用Java语言编程实现,并通过Windows7旗舰版CPU i5 7500 3.2 GHz平台进行运行。 表1 实验数据集 在本文提出的属性约简算法中,邻域半径是一个输入参数,目前的研究结果表明[5],邻域半径取值不恰当可能会对属性约简的结果产生一定的负面影响,因此,本节将研究邻域半径的设定问题。 按照其他文献的研究方法[3-4,9,13],将邻域半径选取一系列的值分别进行实验,这样每个邻域半径下都会得到对应的属性约简结果。然后将得到的属性约简结果利用支持向量机(SVM)和朴素贝叶斯(NB)两种分类器分别进行分类训练,评估出该属性子集对应的分类精度,利用多种分类器进行分类精度评估,使得结果更具一定说服力,从而验证实验结果的稳固性。最后,对每个数据集的结果进行观察,选择出属性约简结果较小且分类精度较高的约简集作为最终的属性约简结果,其对应的邻域半径作为最佳的属性约简邻域半径。本实验设定邻域半径在区间[0.05,0.5]内以0.05为间隔分别取值进行实验,得到属性约简结果和对应的分类精度结果如图2所示。 (a) Heart (b) Hepatitis (c) Horse (d) German (e) Sick图2 邻域半径与属性约简分类精度结果 观察图2可以发现,随着邻域半径逐渐增大,其选择出的约简集也逐渐增大,这主要是由于随着邻域半径的增大,其每个对象的邻域类也逐渐增大,这种增大弱化了对属性的区分能力,因此约简后的属性会逐渐增多。然而,属性增多的同时,分类精度表现出了另一种变化规律。一开始分类精度逐渐增大,达到一定值后不再增大或逐渐减小,这主要是由于一开始属性增多时,进行分类的性能越好,当属性增加到一定程度时,新加进来的属性可能会影响数据的分类,因此数据的分类精度反而降低。所以邻域半径选择过高或过低都不能得到很好的实验结果。分析图2可以看出邻域半径选择为0.2左右最佳,因此本实验将邻域半径设定为0.2进行实验。 图3为三种对比算法和本文算法的属性约简效率比较结果图,横轴为实验数据集,纵轴为时间(单位s)。观察比较结果可以发现,参与比较的文献[14]算法具有较大的属性约简用时,而文献[5]算法、文献[13]算法和本文算法的用时较少一些,其中文献[13]算法的用时稍高,文献[5]算法用时稍低,本文算法的用时位于二者之间。这主要是由于文献[5]算法是基于邻域依赖度的属性约简算法,而本文算法是邻域组合度量属性约简,在文献[5]算法的基础上增加了邻域知识粒度,因此约简时的计算量会稍高一下,但是整体的差距不是特别大。 图3 各算法属性约简时间比较 表2所示的是3种对比算法和本文算法的属性约简集大小的比较结果,观察可以发现,本文的算法得到的约简集大小整体上比其他3种算法的约简集要小一些,例如数据集Horse、German和Sick。这主要是由于多种度量方法对属性的选择方面更加严格,同时对属性的分类性能评估得更加精准,从而使得选择出的属性更加的少。 表2 各算法属性约简结果比较 表3为三种对比算法和本文算法的属性约简集在SVM和NB两种分类器下分类性能比较结果。观察表3可以发现,在大部分数据集中,本文所提出的属性约简算法的分类精度提高了2%~3%,例如数据集Hepatitis、German和Sick。这主要是由于多种度量方法的组合度量能够对属性的各方面能力进行性能评估,从而可以对分类更为关键的属性进行有效的鉴别,因此本文算法得到的约简结果具有更高的分类精度。 表3 各算法属性约简结果分类精度比较 % 综合实验的各方面比较可以看出,本文所提出的邻域组合度量方法在混合信息系统中具有更好的属性约简效果。 属性约简是一种重要的数据挖掘方法,同时也是一种有效的数据维度约简工具。由于现实环境下数据类型复杂,本文提出一种混合信息系统下的属性约简方法。首先在混合信息系统下提出邻域知识粒度用于对信息系统属性集粒化性能进行评估,然后将邻域知识粒度与混合信息系统下的邻域依赖度进行结合,提出邻域组合度量,并将该度量作为启发式函数来构造属性约简算法。实验结果表明,所提出的属性约简算法具有更好的属性约简效果。
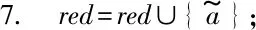
4 实验分析
4.1 实验准备
4.2 参数设定
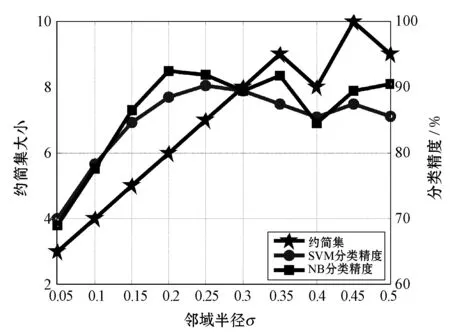
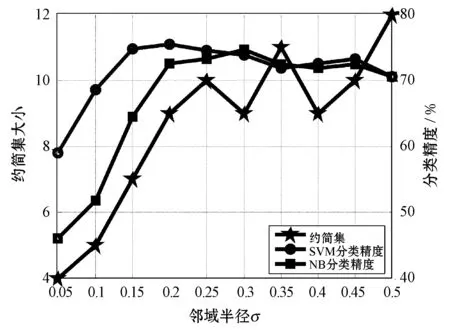
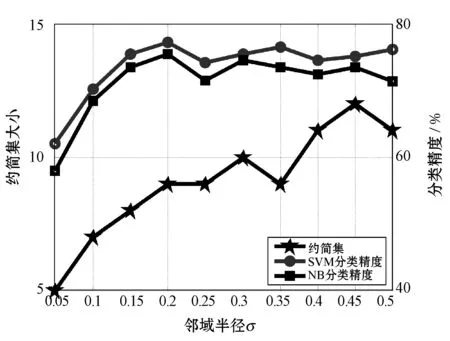
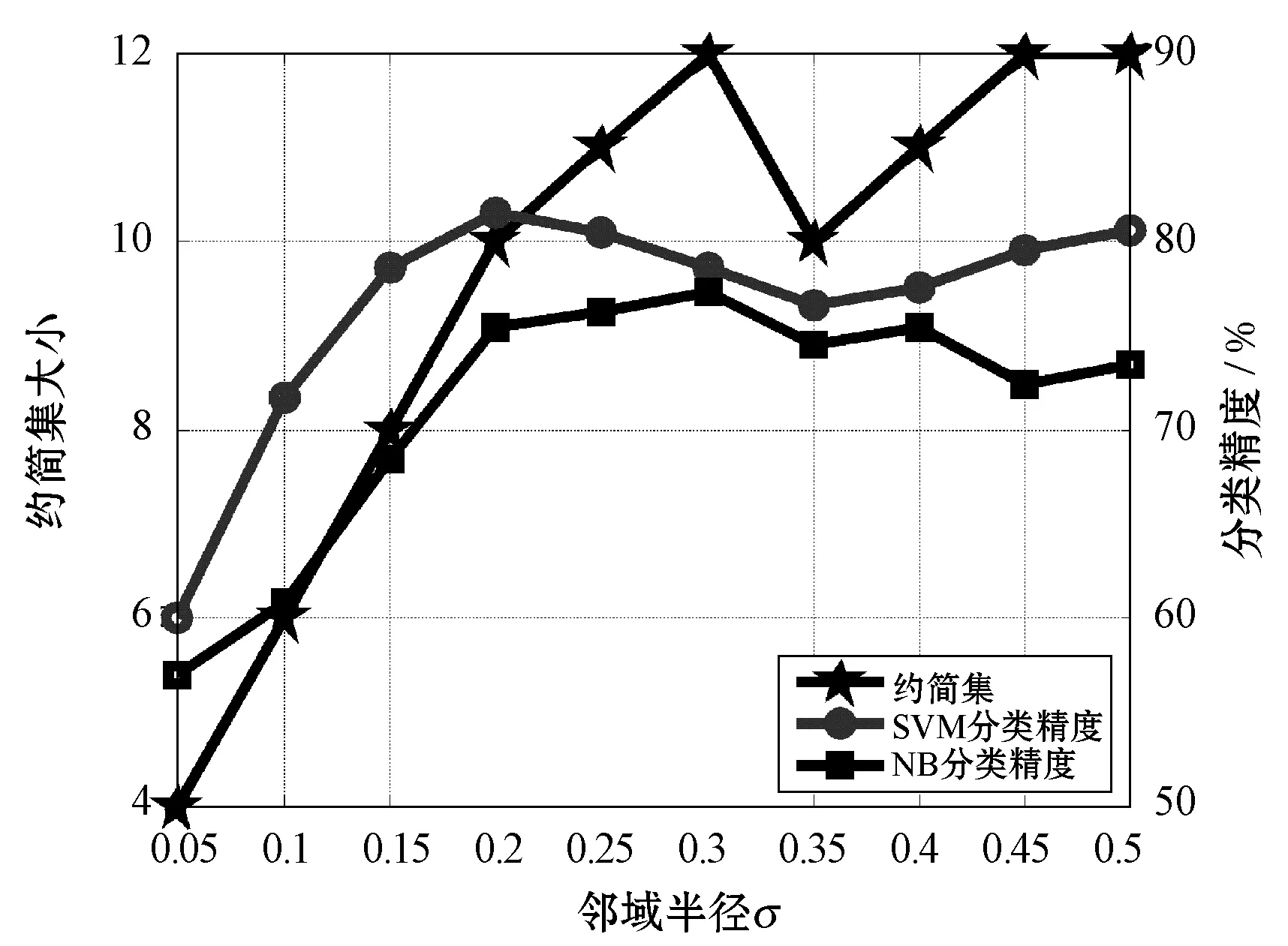
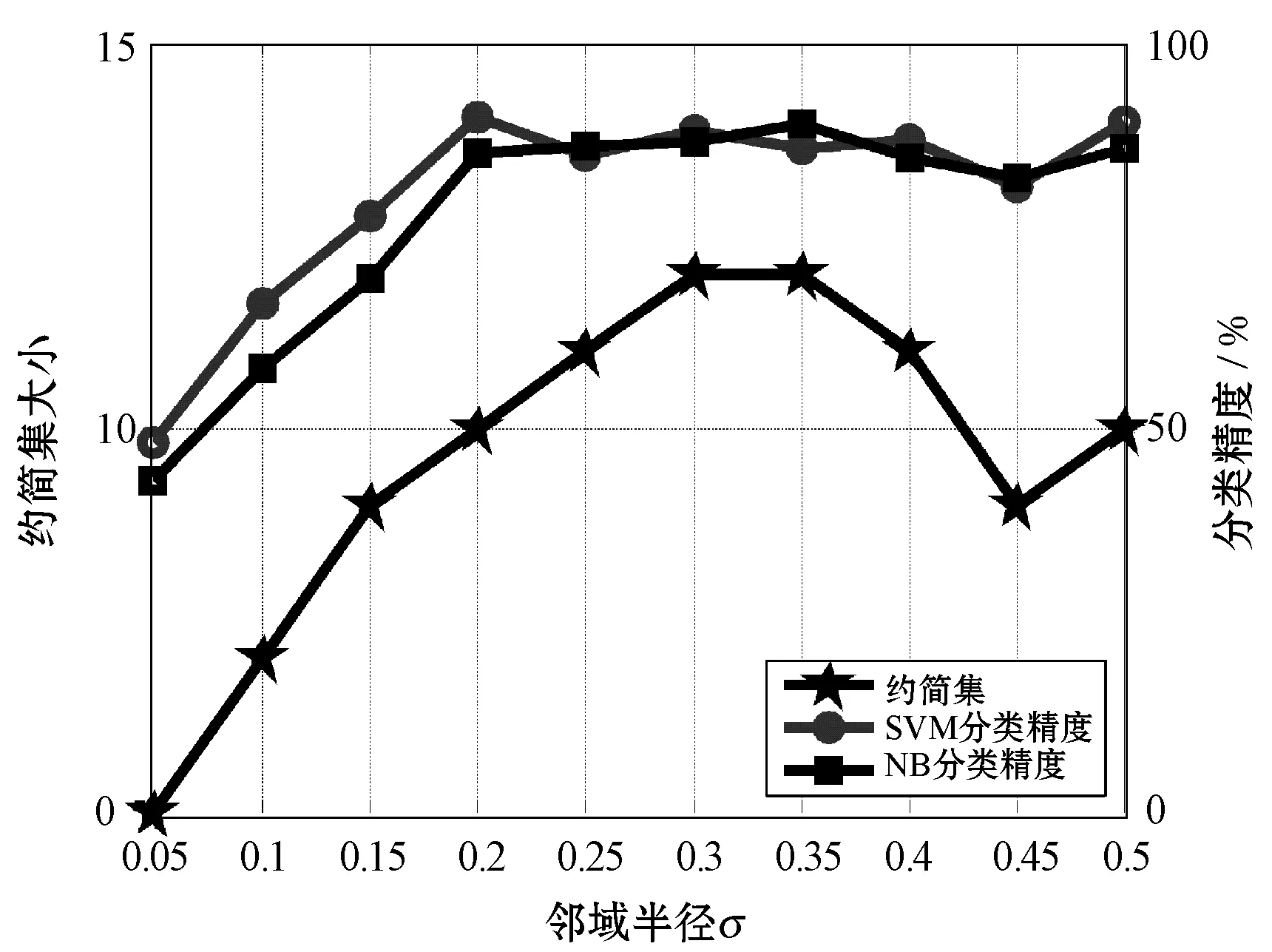
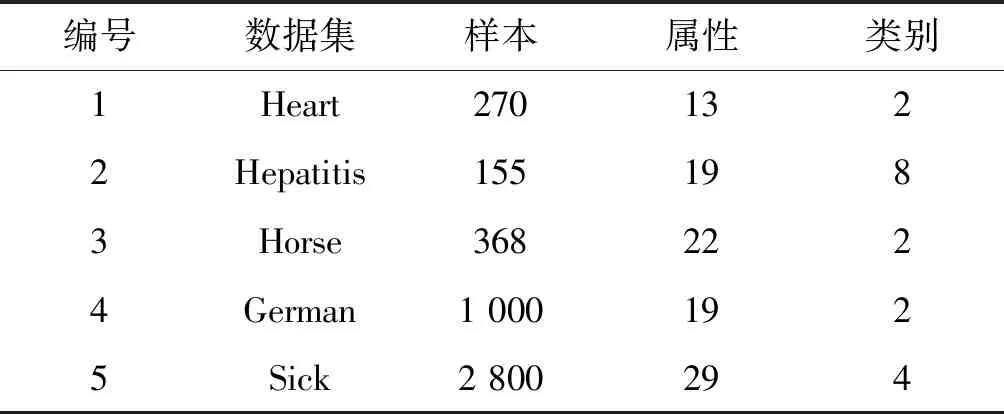
4.3 属性约简效率比较
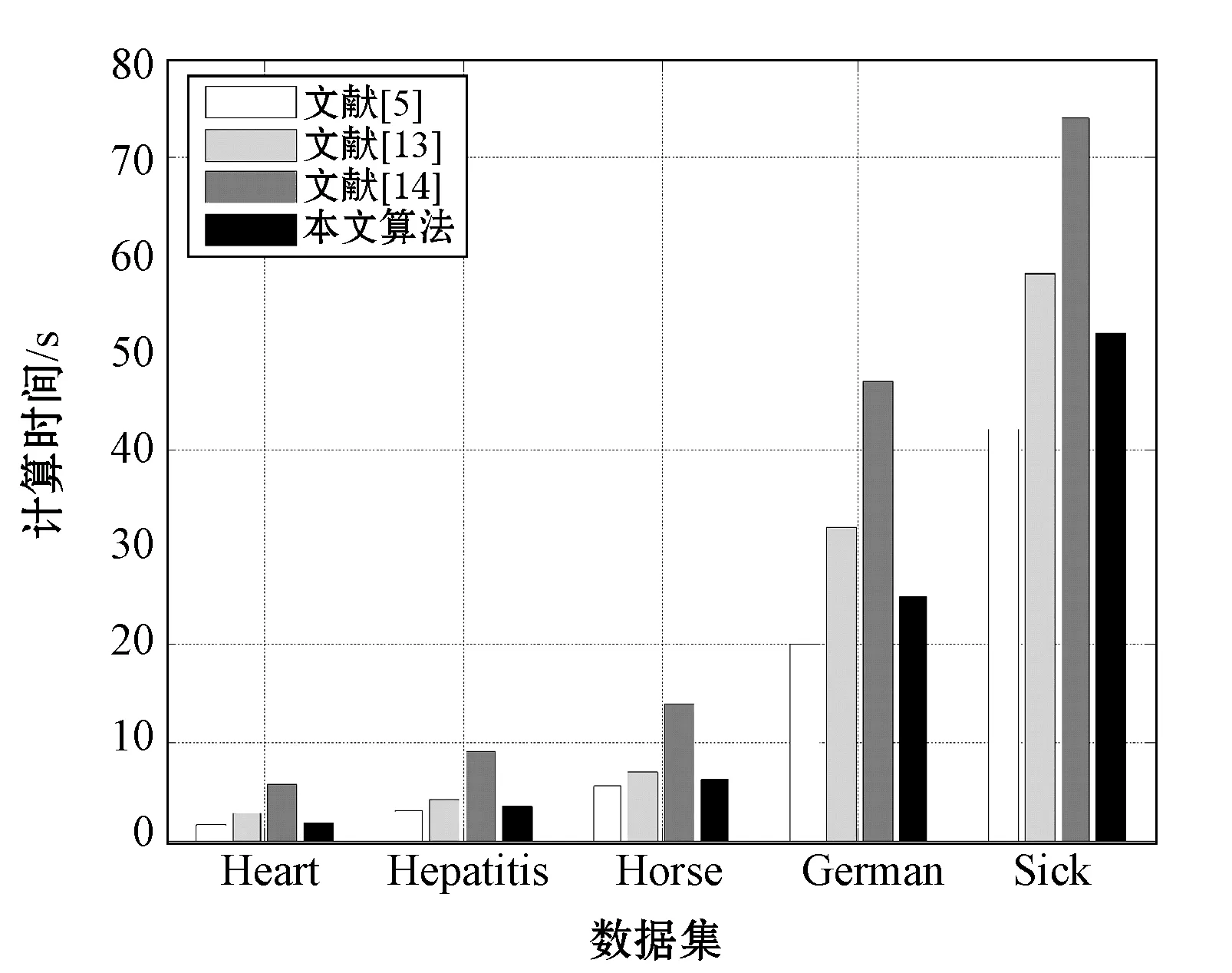
4.4 属性约简结果比较


5 结 语

