超声检测机械臂的系统设计与优化研究

臧艺凯 许剑锋

（1 华中科技大学无锡研究院，江苏无锡，214174；2 华中科技大学机械科学与工程学院，武汉，430074）

0 引言

超声探测技术从20 世纪30 年代左右开始作为金属物体内部检测缺陷检测的一种重要手段，在工业检测领域得到快速发展。目前在国内外，超声检测技术已成为使用最频繁、发展最迅速的一种检测技术[1]。现代工业金属零件的发展，要求超声检测技术有以下几个特点：高速、高精度、高分辨率、高可靠性[2]，可实现自动化检测和数字成像。目前诸如航空发动机叶片、船舶用水轮机叶轮、叶片等复杂曲面的零件均有很大的超声检测需求。在该类零件的检测过程中，为保证精度，需要超声探头的中轴线与被检工件的曲面法线具有较高的重合度，如此对于携带超声探头的机械臂的灵活性提出了较高的要求。在国外，借助于研制专用的检测机械臂，实现超声检测的自动化，仍然是现在的主流趋势[3]。

目前，典型的产品有美国通用公司的超声波检测机器人、英国Ultrasonic Sciences 公司研发的Twin 6 Axis Robots 等。但由于国外严厉的技术封锁，国内对于复杂曲面类零件自动化检测方面的研究仍处于起步阶段，高精度的超声检测自动化设备仍然严重依赖于进口，这给国内相关应用企业带来了巨大的成本压力[4]。另外，人工检测不仅效率低、重复精度低，而且劳动强度高。所以，将机器人和超声检测结合起来进行超声检测机械臂系统的研发十分必要。

英国Ultrasonic Sciences 公司开发的一套双机器人协作检测系统（Twin 6 axis robots[5]）如图1 所示，该系统主要用于叶片等大型零件的超声检测。该检测系统包含2 个六轴机械臂，通过增加移动轴，还可以扩展移动向自由度，检测范围可以达到3.5m×2.5 m。

图1 超声检测机器人（Ultrasonic-Sciences）

美国McDonnell Douglas 公司开发了一套自动化的超声检测系统[6]，该系统专为飞机零部件中的复杂曲面构件研制，可实现9 自由度的运动，并且可以在脉冲发生器检测的运动过程中保持与工件表面的垂直度。

北京理工大学的邹志刚等人研制了一套双机器人超声检测系统[7-8]，如图2 所示。其机器人均采用六关节型，为了实现由复合材料制成的一端封闭回转体曲面类零件的自动检测，为机器人特别扩展了一个移动轴。北京理工大学的李信良利用PC-PMAC 运动控制卡开发了一套运动控制系统，借助于MOTOMAN MA1400 产品的6 自由度机械臂的硬件结构[9-10]，并进行了仿真实验。

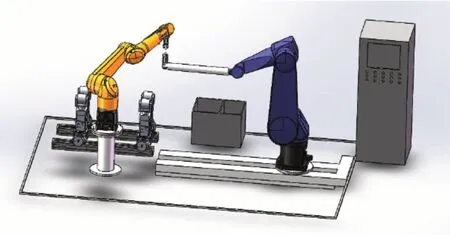
图2 双机械手超声无损检测系统

相比于在商用工业机械臂的末端直接集成超声检测模块和采购进口自动检测设备，自主研制精度可靠、性价比高的超声检测机械臂系统更具有实际意义。本文工作共分4 部分：第一部分介绍客户具体检测自动化的需求，确定超声检测机械臂系统的设计参数和总体方案。第二部分分析机械臂的关键承载部件，并进行拓扑优化，选取最危险受力为分析工况进行分析，得到各部件的应力和位移云图，并评价机械臂局部刚度。第三部分建立机械臂关节坐标系并分析得到机械臂的运动学正逆解、雅可比，仿真并得到各连杆关节的位移、速度和加速度曲线以及机械臂末端xyz方向位移曲线和空间运动轨迹。第四部分利用Newton-Euler 法求解机械臂的动力学方程，利用Matlab 软件分析机械臂动力学并绘制各关节的驱动力（矩）曲线。

1 超声检测机械臂系统设计

1.1 需求分析

如图3 所示，多自由度机械臂系统主要用于特定区域内工件的自动化检测，机械臂系统主要由以下几个模块组成：

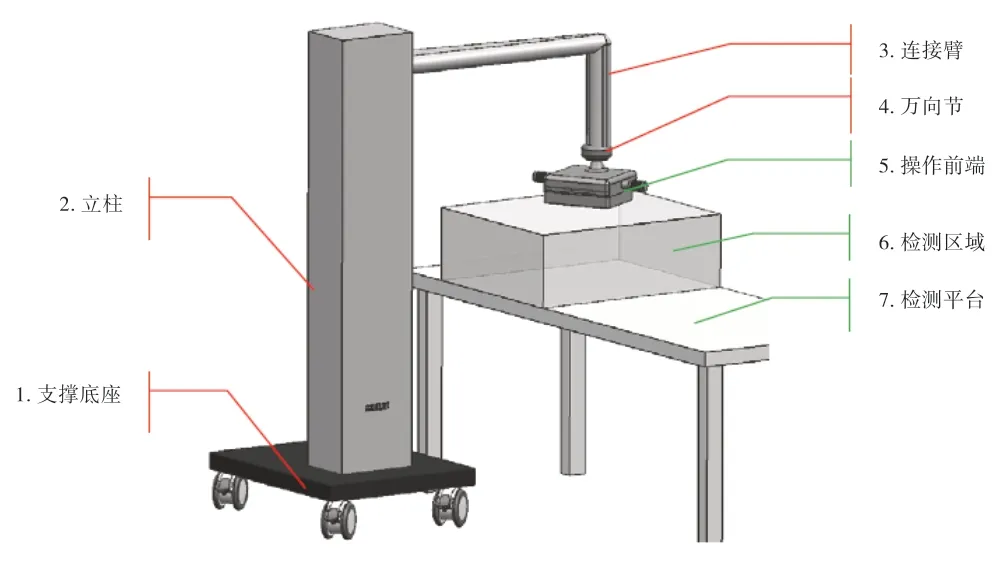
图3 多自由度机械臂系统

1）支撑底座；

2）立柱；

3）连接臂；

4）万向节；

5）操作前端。

机械臂系统主要实现该操作前端在扫描路径中的任意位置的停止和运动。

该机械臂系统的关键参数有：

1）操作前端的上提下压力小于10N；

2）万向节的圆锥顶角不小于60°，且具有自控锁止功能；

3）万向节锁止状态下，操作前端的转动扭矩需大于2.5Nm，所知操作前端的重量为(5.0±0.5)kg。

1.2 系统方案

本机械臂系统携带的操作前端为超声脉冲发生器，其设计是基于脉冲反射法。根据操作前端的操作原理，本文提出如图4 所示的超声检测机械臂的系统方案。本系统中机械臂结构作为数字超声探伤仪的载体，将探伤仪与工控机、机械臂及其相应的驱动系统、位置检测系统有机结合起来。

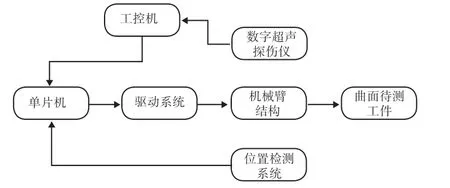
图4 超声检测机械臂系统方案

其主要工作方式如下：根据检测工件的不同，本系统选择相应的扫描路径程序，工控机将命令发送给单片机系统后，单片机根据指令控制驱动系统、自控万向节等驱动装置对零件进行路径点扫描，位置检测系统可以反馈机械臂前端所在的位置坐标，与此同时，超声探伤仪在操作前端加压稳定后，读取该位置的超声图像，并将数据发送至工控机处理并显示。

1.3 方案设计

为实现系统方案设计中的要求，本文针对超声检测机械臂系统结构进行了详细设计。经细化分析，将机械臂总体结构划分为5 大块：

1）机架模块；

2）主被动升降模块；

3）臂关节模块；

4）自控锁紧万向节模块；

5）机械臂控制系统。

根据以上模块设计出的机械臂结构方案模型如图5所示。

图5 UTArm 超声检测机械臂本体

针对检测区域以及相关需求分析，本文确定了机械臂系统UTArm 的详细技术参数，如表1 所示。

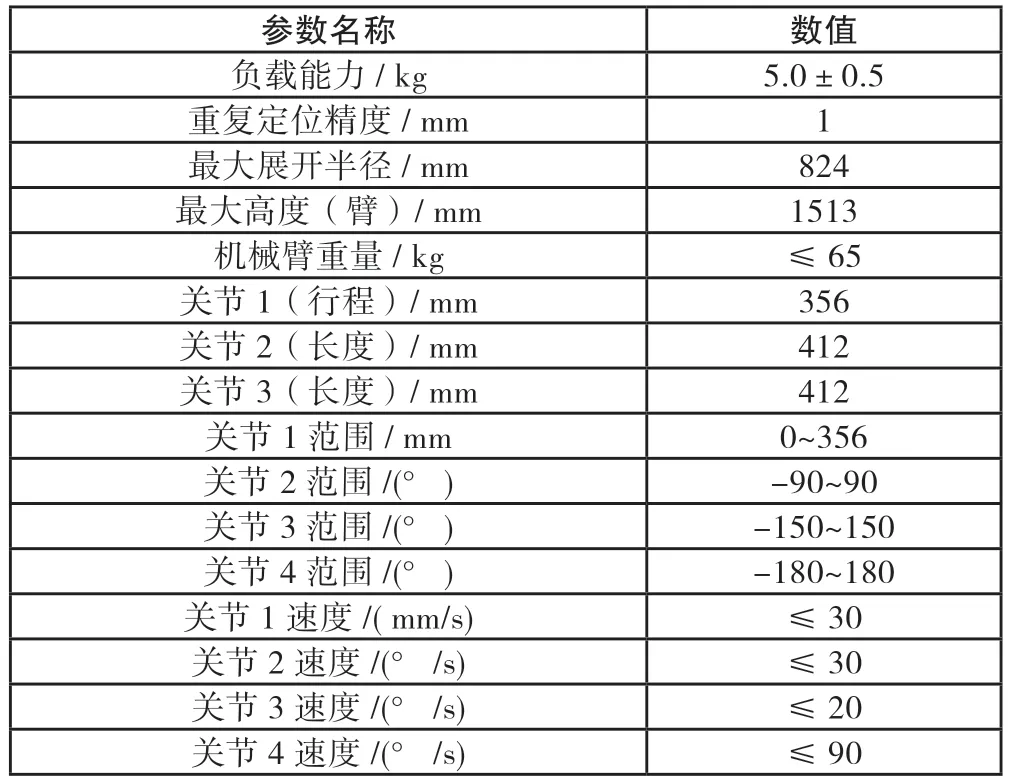
表1 UTArm 机械臂的主要技术参数

1.4 控制系统

UTArm 机械臂控制系统如图6 所示，其主要由驱动和检测元件组成，包括：计算机，单片机与辅助硬件电路，显示面板，关节1～3 步进驱动器，升降定位控制器，电推驱动器，压力传感器及相关限位开关等。关节1～3 步进驱动器是三个关节轴电机的驱动。

图6 UTArm 机械臂控制系统组成

超声检测机械臂UTArm 样机如图7 所示，机械部件安装完成后，笔者团队测试自控锁紧万向节的响应速度和锁紧力矩均满足设计需求。压力传感器可以实时反馈压力值至控制系统并且显示到监控面板上。机械臂的控制模块集中安装在背部的控制柜内，这既提高了整体走线的合理性，又提升了控制系统的整体抗干扰能力。经样机测试证明，超声检测机械臂系统的设计合理。

图7 UTArm 样机

2 UTArm 关键部件优化

在机械臂整体结构的设计中，本团队对其关键部件进行了优化设计，目的是在保证设计的刚度和轻度情况下，尽可能地优化结构设计，减轻整体的自重，以改善机构和设备的整体性能。

为了减轻升降电机的负载，提升其动态性能，本团队对机械臂的大臂基座进行了优化设计：将机械臂关节的4 个极限位置的等效力和力矩作为最危险工况进行仿真分析和拓扑优化，经过统计得到的臂基座的极限载荷工况如图8 所示，而这4 种工况下机械臂关节对于基座的等效力和力矩如表2 所列。

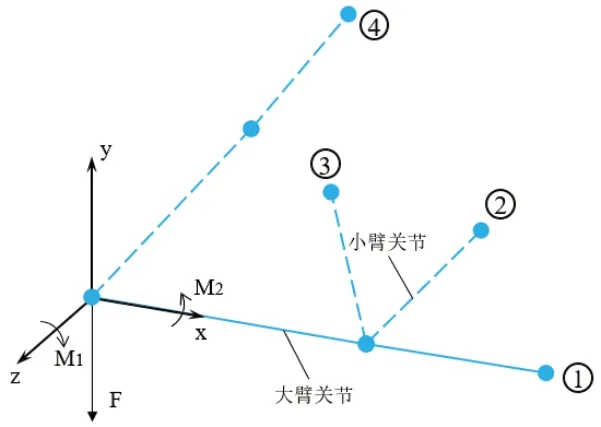
图8 臂基座极限位置

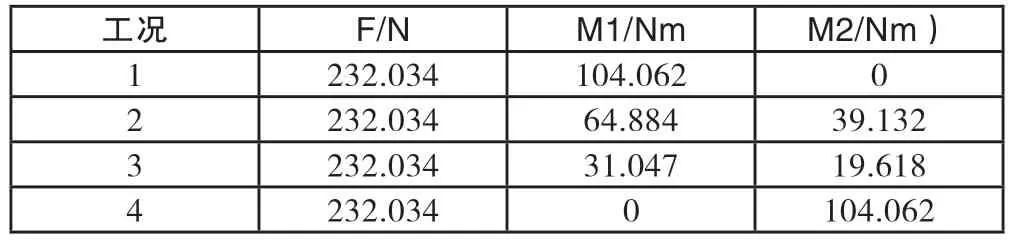
表2 臂基座等效力矩（力）

将优化前的臂基座模型导入至ANSYS Workbench中，设定目标，减少材料60%，约束条件为4 种极限危险工况。输出结果如图9 所示。其中，零件红色部分为应力较小的部分。基于此结果，本团队利用三维软件对臂基座进行重新设计，作为下一步静力学分析的准备。

图9 臂基座4 种工况优化结果

根据图9 中的臂基座拓扑优化结果，本团队在模型上开设减重槽，模型优化后，经测量，基座质量从原始的3.401 kg 降至2.032 kg。重新将模型导入ANSYS Workbench 进行静力学分析，加载的边界条件依然是4种极限位置的危险工况。经过分析，得到臂基座在4 种极限工况下的应力与变形结果如图10 种所示。

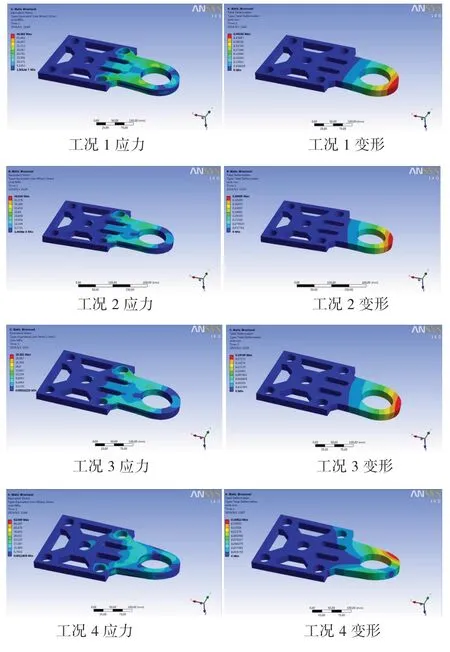
图10 臂基座应力与变形云图

从图10 可以发现，优化后的臂基座所受到的最大应力和变形都是发生在工况1 时，最大应力为46.668 MPa，6061 铝合金的屈服强度为276 MPa，最大应力处远小于屈服强度。最大的变形0.491 mm，位于图10 红色区域，变形量相对较小。其他的三组极限工况下的最大应力与变形值见表3。

表3 臂基座仿真最大应力与变形

为了进一步改善臂基座的局部变形，本团队将该零件设计为分体式。即：基座板和关节套筒分别加工，再用螺钉装配，如图11 所示。如此方法可以降低加工成本和加工难度，又可以通过螺钉的预紧力减小整体变形。安装测试表明，本优化在应力和变形方面改善明显。

图11 臂基座实物图

3 UTArm 运动学建模

3.1 UTArm 的正运动学求解

超声检测机械臂UTArm 是串联型机械臂，包含4 个自由度：移动副1 个和转动副3 个，这与传统的SCARA机械臂不同，因为UTArm 的移动副在机械臂的基部。

参考D-H 坐标系，分别建立UTArm 的各关节坐标系，如图12 所示。

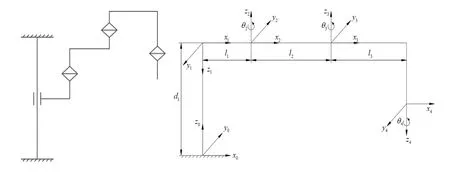
图12 超声检测机械臂UTArm 连杆坐标系

由图12 可得到UTArm 的各连杆的D-H 参数，具体见表4 所示。

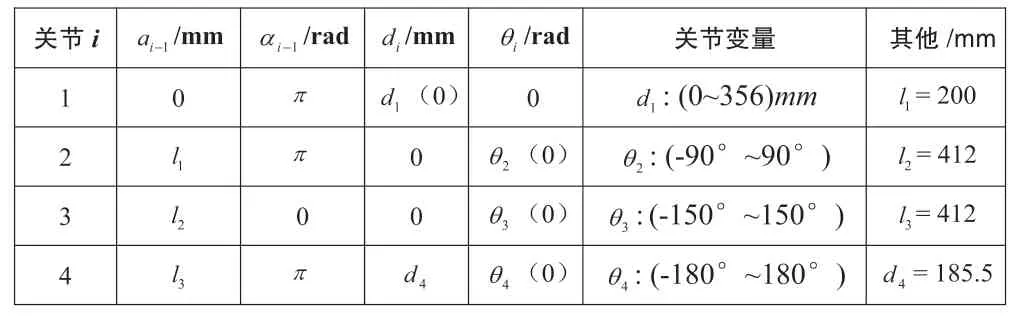
表4 超声检测机械臂UTArm 的D-H 参数表

UTArm 的运动学正解是为了求出其手臂变换矩阵，以描述机械臂的末端连杆坐标系相对于基坐标系的位姿。由D-H 法建立坐标系的规则和连杆描述的4 个参数，可以表示出两连杆间的坐标变换通式。

求解超声检测机械臂UTArm 的正运动学目的是：求出其机械臂的位姿变换矩阵，得到机械臂的末端连杆坐标系与基坐标系间的数学关系。

根据D-H 法坐标系的建立规则以及表4 中的连杆参数，可以表示出两连杆间的坐标变换通式如公式（1）所示：

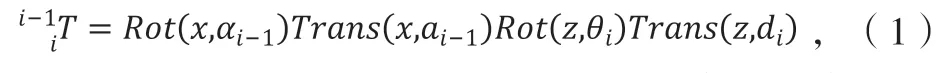
可得末端连杆{n}相对于基坐标{0}的位姿矩阵变换式为：

由表4 中UTArm 各连杆的参数，即可得出超声检测机械臂UTArm 的“机械臂臂变换矩阵”

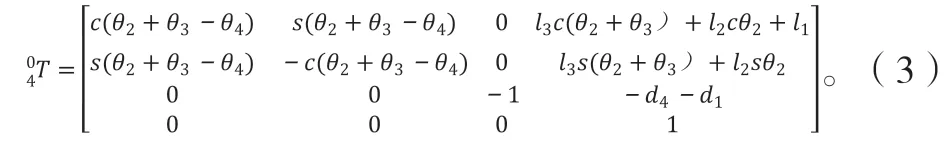
超声检测机械臂UTArm 的工作空间可以通过Matlab进行数值仿真得到。如图13 所示，把基座标作为原点，从此关节向末端设定固定的步长，即可得到超声检测机械臂UTArm 的工作空间云图，图13 的右侧是机械臂工作空间的俯视图，通过工作空间绘制，可确认设计的机械臂连杆参数满足检测区域的需求。

图13 机械臂工作空间三维图（左）和平面图（右）

3.2 UTArm 的逆运动学求解

超声检测机械臂UTArm 的逆运动学研究的目的是得到机械臂的关节参数、末端执行器TCP（Tool Center Point）位姿矩阵和各关节运动变量之间的数学关系。即通过位姿求得关节变量值，驱动器就可以计算每个关节到达该位姿需要的脉冲数。

UTArm 计算的具体过程如下。

压汞孔隙分析是目前测量孔隙分布的经典方法，适合测试干燥试样的孔隙分布。初始压实状态下的试样孔隙分布特征如图6所示。

将超声检测机械臂UTArm 的运动方程写成：

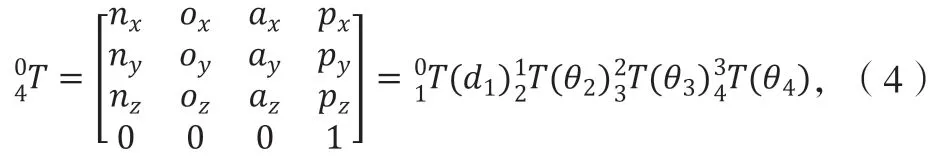
由矩阵中元素(3，4)对应相等可求得：

由公式（5）中的矩阵元素(1，4)和(2，4) 分别对应相等，可解得：

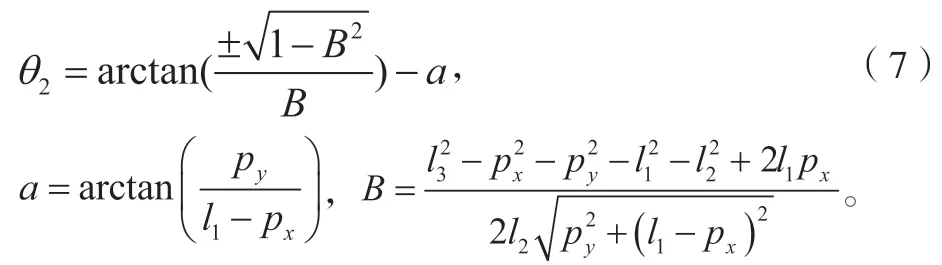
3）解关节变量θ3：

由式（5）中的矩阵元素(1，4)和(2，4) 分别对应相等可解得：

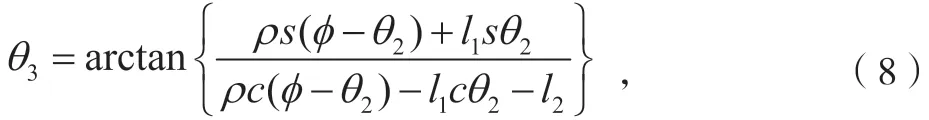
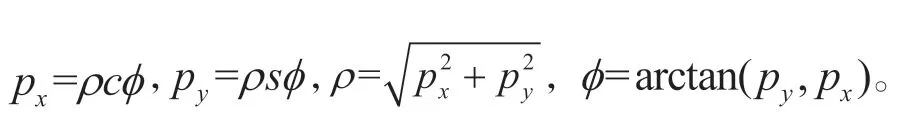
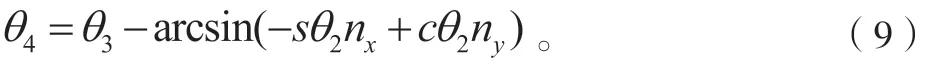
3.3 UTArm 的雅可比矩阵

求解超声检测机械臂UTArm 的雅可比矩阵，目的是获得操作速度与关节速度的数学关系，也可以理解为从关节空间到操作空间的传动比[11]，可通过如下公式计算。

微分变换法是以微分运动和广义速度之间的映射关系建立起来的，本文也用此法来构造UTArm 的雅可比矩阵。该法的微分运动矢量方程如下所示：

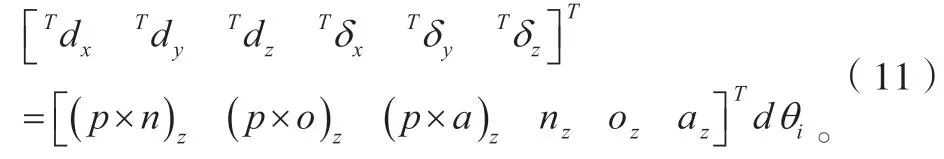
雅可比矩阵表示为：

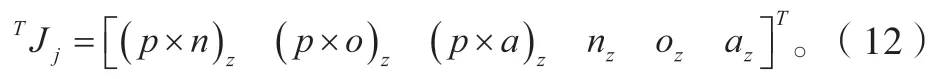
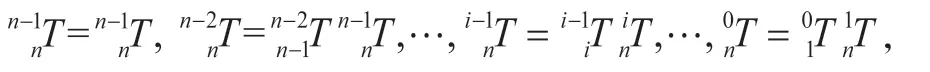
再由式（12）可得出UTArm 的雅可比矩阵，各列如下：

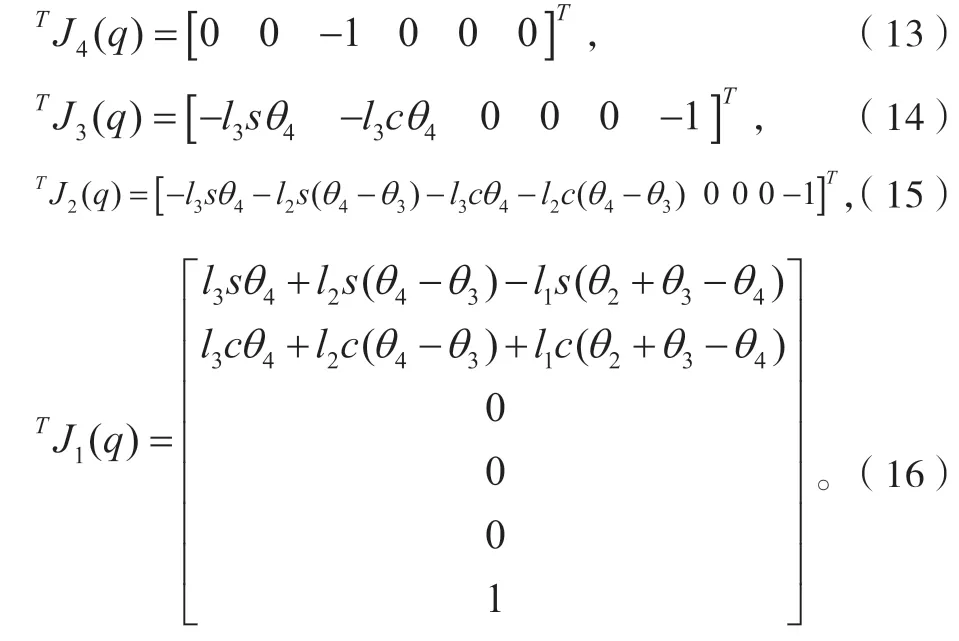
最终求得超声检测机械臂UTArm 雅可比矩阵为：

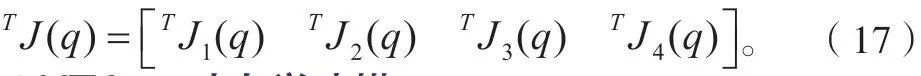
4 UTArm 动力学建模

分析超声检测机械臂UTArm 的动力学，目的是根据各关节的质量、连杆末端的负载和传动机构的特征进行动力学计算与仿真，以确定传动机构的合理性。在操作前端以设定的速度和扫描轨迹进行检测任务时，确定各驱动器、电机所提供的驱动力（力矩）的大小是否满足使用需求。分析结果也可以为驱动器的选型和控制程序的编写提供参考依据。

为了建立机械臂的动力学方程，要先计算出相关的参数，包括：相邻关节连杆坐标系间的原点矢量、关节连杆的质心坐标等等。首先，通过超声检测机械臂UTArm 的坐标系得到相邻连杆的坐标系原点矢量，如表5 所示。

表5 相邻连杆的坐标系原点矢量

再由三维设计软件Solidworks 中设计的模型和材料属性，可以在软件中建立相应的坐标系。通过软件中的测量工具，可以得到机械臂各关节连杆的质心在连杆坐标系中的坐标，惯性张量、质量。具体测得的各参数值见表6。

由于机械臂结构复杂，为便于进行动力学方程求解，需要对机械臂进行必要的简化，简化后的示意图如图14所示。

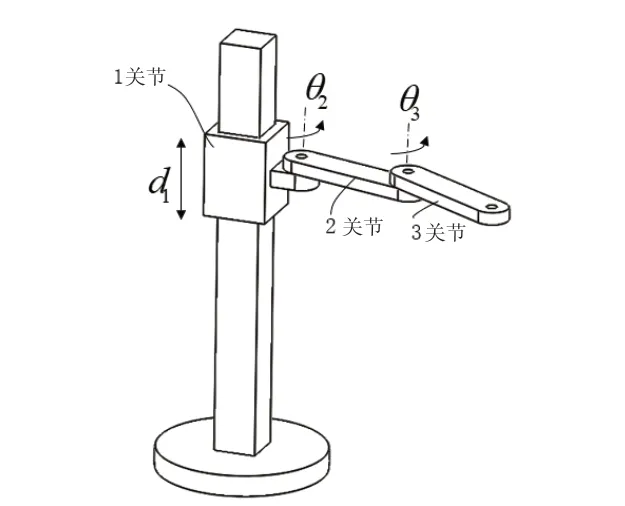
图14 机械臂关节简化图

本文进行动力学计算采用的是牛顿欧拉法，结合上述运动学方程，可以求出机械臂连杆1、2、3 的如下参数：角速度；角加速度；线加速度；质心线加速度；质心惯性力；质心惯性力矩等。最后求得各关节转速与力矩间的关系，如此求得各关节的驱动力（矩）如下所示。

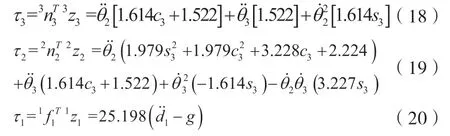
将上式（18）、（19）、（20）在Matlab 对机械臂进行逆向动力学仿真，结合其正向的动力学相关参数，可以得到如图15 所示的仿真结果，即机械臂1#关节的输出力曲线，和2#3#关节的输出力矩曲线。

图15 三关节力和力矩曲线

从以上仿真结果可知，机械臂移动关节1 的负载力范围为247.8N～ 246.2 N，与折算到丝杆上的负载合力387.5 N 相比，仿真负载力较小，证明了该关节轴的电机选型合理。由关节2 和3 的力矩曲线可知，关节2 的力矩值分别在0.8 s 和3.2 s 左右达到约2.8 Nm 和1 Nm（反向），关节3 负载力矩在0.8 s 达到约2 Nm，在3.2 s 达到约1.5 Nm（反向），曲线平滑。仿真结果证实了升降电机和臂关节电机选型的合理性。

5 结语

本文设计了一款UTArm 超声检测机械臂，用以满足特定检测需求的超声检测机械臂系统，并分析了超声检测机器人的国内外现状，完成了机械臂的机械结构本体和控制系统设计。本文在对系统机械和控制部分详细设计的基础上，根据机械臂的具体参数，系统地研究了机械臂的运动学和动力学，建立了机械臂的运动学和动力学模型，并对机械臂运动学及动力学模型进行仿真分析并验证。本方案为实现超声检测的自动化提供了新的思路。