基于含双对称矩形短柱MIM波导的Fano共振及其传感应用的研究*

陈剑峰，戚大伟,田 赫

(东北林业大学)

0 引言

传统光学的衍射极限极大限制了如集成光学、纳米光学等现代光学的发展.而表面等离极化激元(Surface Plasmon Polaritons)的提出，则给光子器件的发展带来更多可能[1-3].SPPs由金属表面的自由电子与入射光子相互耦合产生.其沿金属-界面传播，且能在亚波长范围内实现对光操控[4-6].在众多基于SPPs的波导器件中，金属-绝缘体-金属(Metal-Insulator-Metal)型光波导是其中最突出的一种.这种光波导结构紧凑、成本较低且对SPPs束缚性较强.迄今为止，已有多种MIM型表面等离激元光波导被设计及制造.如滤波器[7-8]，波分复用与解复用器[9-11]，耦合器[12-14]以及布拉格反射器[15-17]等.与传统洛伦兹线型相比，Fano共振产生的谱线呈非对称型，具有显著的光谱对比度.由于Fano共振对几何参数和介质环境非常敏感，其多被应用于折射率传感器.因此，基于MIM型表面等离激元波导结构的Fano效应更是受到科研人员的广泛关注.2017年Yan等学者制作了由多个谐振腔结构干涉激发的Fano共振纳米传感器[18]；2018年Zhang等学者设计了由矩形谐振器和双侧耦合圆环谐振器组成的双MIM波导传感器[19]；2019年Qiao等学者设计了由M型腔和挡板构成的MIM波导传感器[20]；2020年Liu等学者设计了由D型腔构成的MIM波导传感器[21].在这些结果中，尽管许多结构具有良好的灵敏度和传感特性，但它们相对简单，可调参数较少.因此，Fano谐振的灵活可调性需要在不同结构中进行更多的讨论，多参数结构的出现可能有利于MIM波导器件在传感领域的发展.受文献研究结果的启发，该文设计了一种由双对称矩形短柱波导(DSRSW)耦合椭圆形开口环谐振腔(CSRRC)组成的表面等离激元MIM波导结构.CSRRC中的分裂环打破了结构的对称性，耦合DSRSW后，可以实现双Fano共振.利用有限元方法对结构的透射谱进行数值模拟.优化几何参数后，计算了结构的灵敏度及最大品质因数FOM.

1 结构与方法

1.1 结构

图1所示为结构的X-Y横截示意图.w是波导的宽度，L是CSRRC的开口宽度，a和b是CSRRC的长轴和短轴，s、h、d是矩形短截线的间距、高度和宽度，H是耦合间隙高度，g为银挡板的宽度.设计的结构为三维结构，但在Z轴方向上，结构的高度足够高时，可被看作二维结构.不仅计算结果相同，同时降低了计算的复杂性.示意图中橘色区域代表银，白色区域代表空气.为保证波导系统中仅存在横向磁模(TM0)在SPP波中传输，固定w=50 nm,a=150 nm,b=100 nm，且整体结构相对于参考线对称.

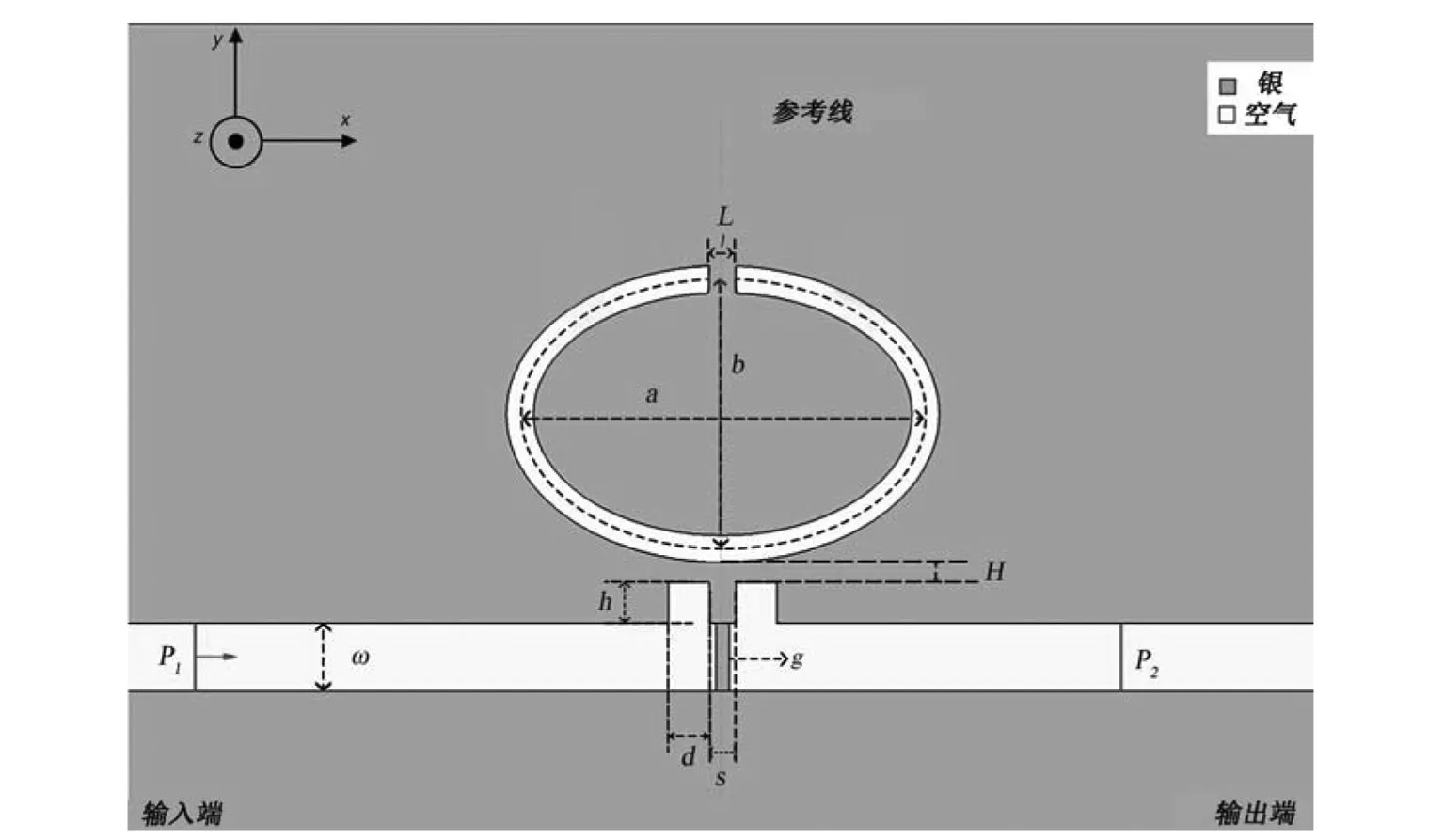
图1 DSRSW和CSRRC组成的表面等离激元波导结构的示意图

1.2 方法

为便于分析结构的光学传输特性，该波导结构的几何模型由COMSOL Multiphysics 5.4a建立，有限元方法(finite element method)进行数值模拟.为保证计算的精确性，选用超细网格保持收敛性.选用完美匹配层(PMLs)设计了如空气的折射率，银的相对介电常数以及结构参数等.PMLs可以隔离反射波进入结构，并且可以有效吸收结构内部的光波.经过模拟计算后，得到了该波导系统的透射光谱.透射率用T=(S21)2表示，S21为输入端p1至输出端p2的透射系数.空气的相对介电常数为1，而银的相对介电常数由Debye-Drude色散模型定义：

(1)

式中ε0=-9530.5为静态介电常数，ε∞=3.8344为无限频率介电常数，σ=1.1486×107s/m为银的电导率，τ=7.35×10-15s为弛豫时间，ω为输入波的角频率.

横向磁模(TM0)用下式定义：

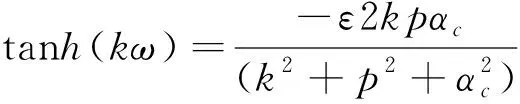
(2)

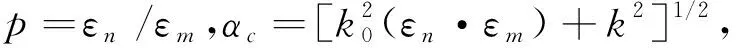
透射波长可由驻波理论得出：

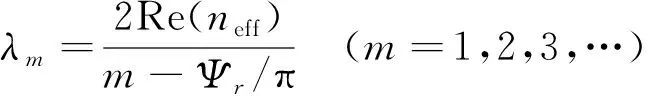
(3)

(4)

其中Re(neff)是波导中波长的有效折射率的实部.Ψr是腔的一端反射光束的相移.

此外，通常用耦合模式理论(coupled mode theory)分析等离子体共振系统中的单模耦合.但当涉及多模式耦合时，每个谐振模式的耦合相位和模量是不同的，这些都会影响传输.因此，采用多模干涉耦合模理论(multimode interference coupled mode theory)分析结构的传输谱：

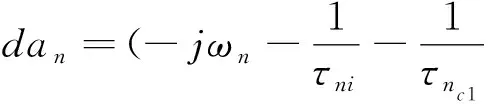
(5)

(6)

(7)

Sn,1+=γn1ejφn1S1+,Sn,2+=γn2ejφn2S2+

(8)

其中，其中an和ωn分别是第n-th个谐振模式的归一化幅度和谐振频率.τni是谐振器中第n-th个谐振模式的内部损耗的衰减时间，其中τnc1和τnc2是谐振器与波导间耦合的衰减时间.

2 结果与分析

为了明确所设计结构的传输特性，除上述固定值外，还设置了以下结构参数：L=20 nm,s=20 nm,g=10 nm,h=30 nm,d=25 nm,H=10 nm.

2.1 Fano共振线形成因

图2展示了整个结构、单DSRSW、单CSRRC的透射光谱.可以看出，整个结构的透射谱线(蓝色实线)具有明显的不对称尖锐峰.说明所设计的结构激发了由连续宽带状态和离散窄带状态相互作用引起的Fano共振.其中，DSRSW的透射谱具有较高的透射率，可被认为是连续的宽带状态.而单CSRRC的透射谱与洛伦兹线形类似，可认为是离散的窄带状态.该结构激发了两个Fano共振峰.与左侧共振峰相比，右侧共振峰的半宽度更大，此时结构的灵敏度更好.因此，下面将主要研究右侧的共振峰.

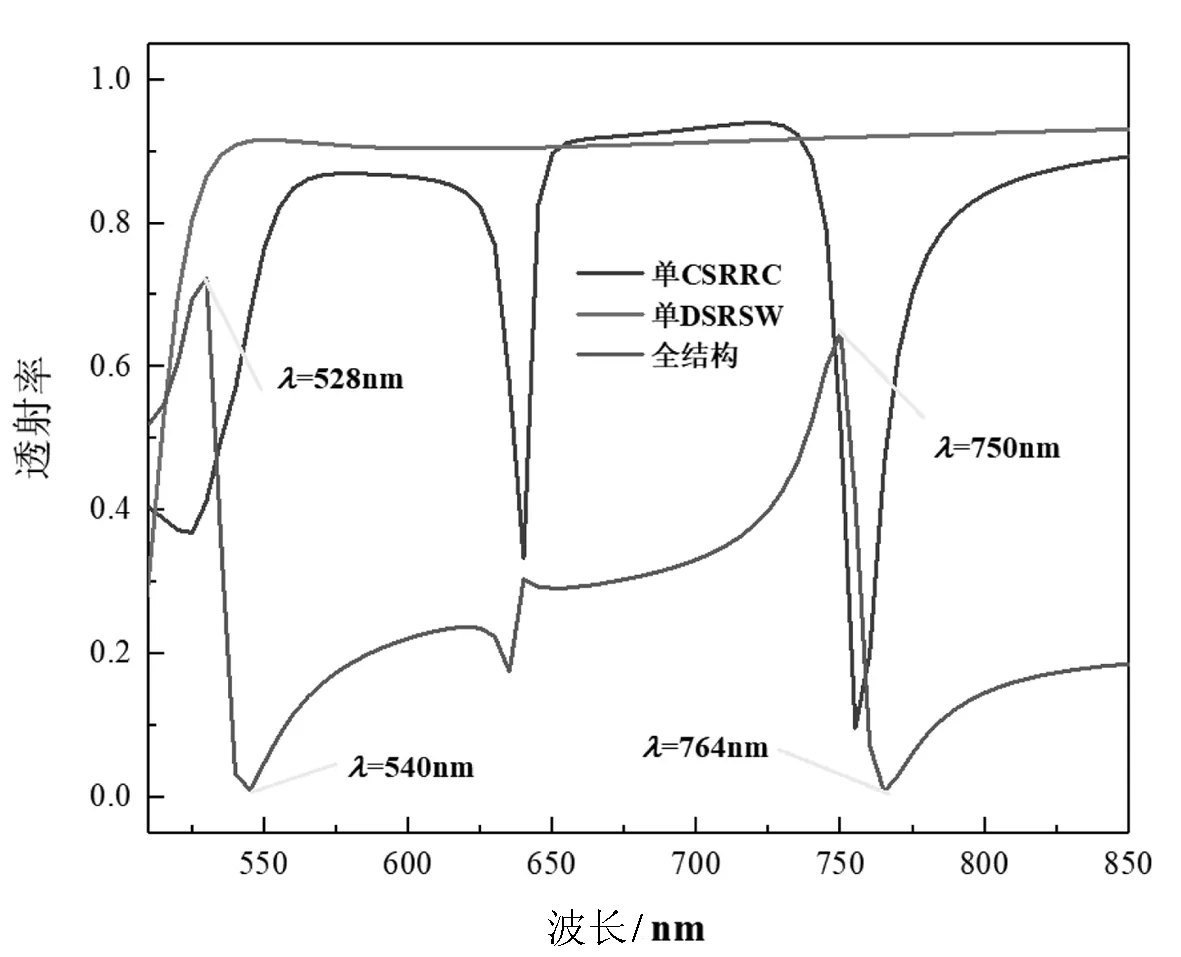
图2 单DSRSW、单CSRRC及整个结构的透射光谱

2.2 磁场分析

波长λ=528 nm(左侧峰)、λ=540 nm(左侧谷)、λ=750 nm(右侧峰)、λ=764 nm(右侧谷)处的磁场强度|Hz|2如图3所示.谐振器中磁场能量的分布关于参考线对称.从图3(a)～(c)可以看出，在Fano共振峰处，SPPs的大部分能量可以通过结构传输到输出端.而如图3(b)和3(d)所示，在Fano共振谷处，SPPs的能量集中在CSRRC中，不能传输到输出端.

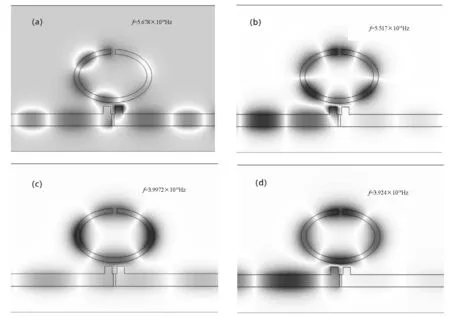
图3 磁场能量分布图

2.3 数值计算

Fano共振可被多种环境参数调谐，而介质折射率的变化对其影响较为显著.接下来，将研究结构的Fano共振在折射率传感中的应用.灵敏度(S)可以衡量传感器的传输特性，通常由公式(9)表示：

(9)

其中，λ为共振波长，n为折射率.

图4(a)展示了不同折射率下结构的透射光谱，折射率变化范围为1.00～1.10RIU，间隔为0.02.可以看出，随着折射率的增加，Fano共振具有明显的红移.图4(b)展示了右侧峰的共振波长与结构折射率之间的关系.值得注意得是拟合直线的斜率表示灵敏度.此时，结构的灵敏度约为821nm/RIU.

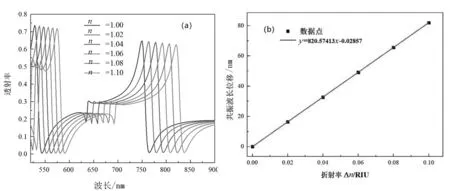
(a)不同折射率下结构的透射光谱 (b)右侧Fano峰共振波长与折射率的关系图4

从图3磁场能量的分布可以看出，SPPs的能量多集中在CSRRC中.因此，将改变CSRRC的几何参数观察Fano共振线形的变化.固定其他参数不变，将CSRRC的开口宽度从10 nm增加到30 nm，间隔为5 nm.从图5(a)可以看出，Fano共振谱线此时具有明显的红移和蓝移.这是由于Fano共振的共振波长由CSRRC激发的窄带离散态决定.改变CSRRC的开口宽度可以做到调谐Fano共振谱线的峰位置及共振波长.图5(b)展示了改变开口宽度后结构的灵敏度变化，可以看出，此时结构的灵敏度变化较小.

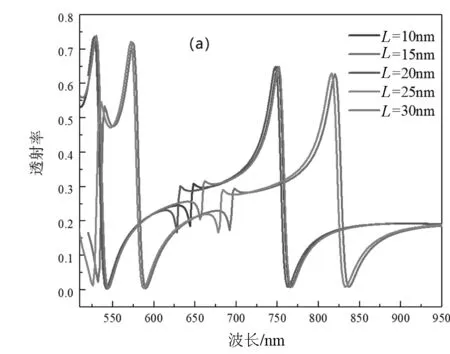
(a) 改变开口宽度后不同折射率下结构的透射光谱

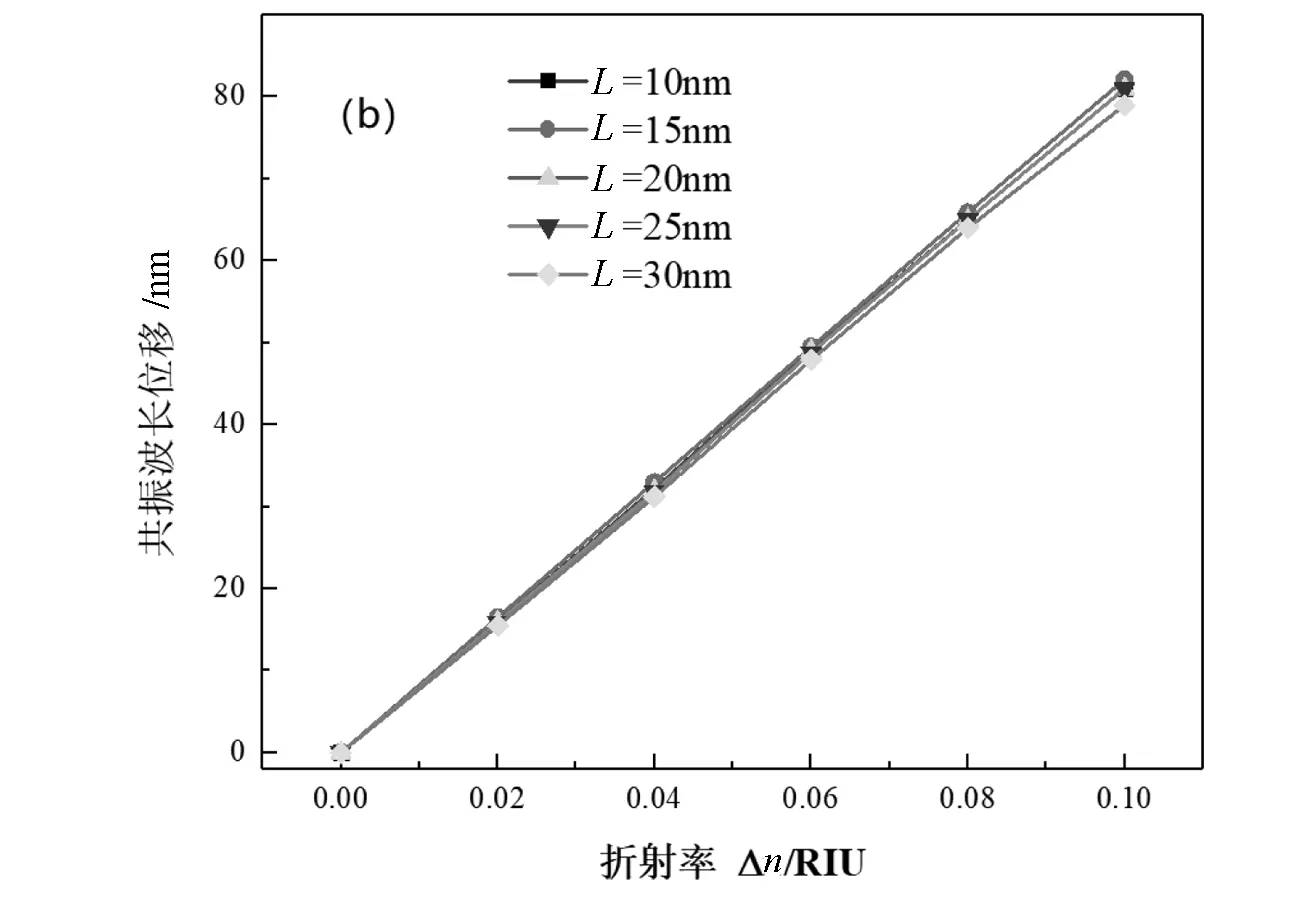
(b)右侧Fano峰共振波长与折射率的关系图5

另一方面，品质因数FOM(figure of merit)也是评价Fano共振传感特性的一项重要指标.在传感应用方面，高FOM值也是首选.其可用式(10)表达：

(10)

其中T(λ)是透射率，而dT(λ)/dn(λ)是折射率引起的透射率变化.由此知道，指数变化引起的超尖峰和超低谷将会获得高FOM值.优化几何参数后，计算了所设计结构的FOM值.当几何参数为：L=20 nm,s=20 nm,g=10 nm,h=30 nm,d=25 nm和H=10 nm时.如图6所示，在λ=524 nm,λ=580 nm,λ=822 nm时，结构的FOM值分别为1462，2001，967.

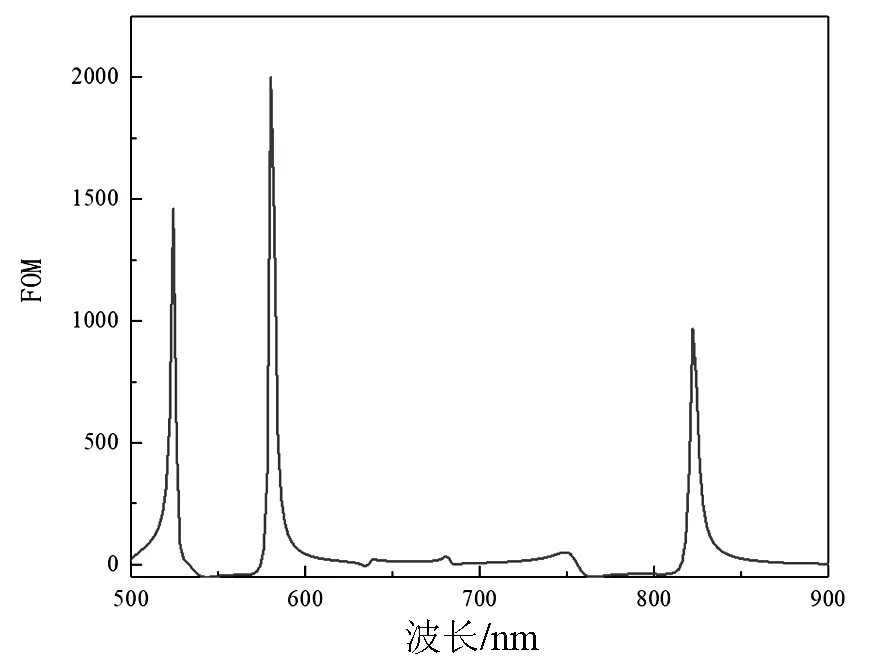
图6 结构的FOM值

3 结论

该文设计了一种由DSRSW和CSRRC组成的MIM型表面等离激元光波导结构.通过多模干涉耦合模理论分析后发现，该结构的Fano共振由CSRRC激发的窄带离散态和DSRSW激发的宽带连续态耦合形成.仿真结果表明该结构支持双Fano共振.共振波长可以通过结构的几何参数进行调整，其主要由CSRRC的开口宽度调谐.优化结构的几何参数后，灵敏度达到821nm/RIU，FOM达到2001.基于这些结果，该种MIM波导结构在纳米折射率传感器，纳米全光开关等领域具有潜在的应用前景.