K-复数的矩阵的性质分析与应用*

蔺 琳,杨 鑫

(大连财经学院)

0 引言

回顾数系的历史发展及数系的扩充，既有在旧的数系之中添加新的元素，也有在旧的数系之外去构造一个新的代数系[1].K-复数是复数的一个重要延伸，即形如a+kbi(k∈R、k≠0)的复数称为z=a+bi的K-复数，记为z(k)它具备复数的所有性质[2].同时，复数与矩阵两大数系之间存在许多共同性，包括数值的转变，矩阵转置以及四则运算等[3].因此，K-复数的矩阵表示方式成为数系研究中的热点之一[4-5].为更深一步的了解矩阵的性质和K-复数的性质，根据现有矩阵的基本运算及其性质，引入了线性变换和线性代数的概念[6-7].该文的重点在于研究K-复数的基本运算与矩阵的基本运算之间的关系、矩阵的其它运算在K-复数性质上的应用和灵活应用K-复数的矩阵表示来解决数学问题.讨述K-复数与矩阵的关系，不仅具有数学理论方面的意义，而且具有较强的现实意义.

1 K-复数相关定义和引理

1.1 K-复数相关定义

K-复数具备复数所具有的性质，所以在该文中关于K-复数的定义和性质是可证明的是具有意义的，在该文中主要给出所要涉及的定义和定理以及一些已经熟知的结果，以便在后文定理的证明及应用中使用.

定义1[2]将a+kbi(k∈R,k≠0)的复数称为z=a+bi的K-复数，记作z(k).

定义2[2]形如a+kbi(k∈R,k≠0)中当a=0、b≠0时，把z(k)=kbi叫作纯K-虚数.

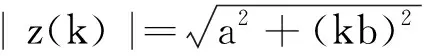
即N是二阶方阵集合，其元素由主对角线元相同、次对角线元上互为相反数的数值组成.

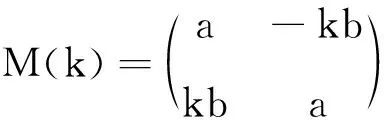
定义5[4]矩阵的加(减)法:设A=(aij)mn，B=(bij)mn是2个m×n矩阵，则矩阵C=(cij)mn=(aij+bij)mn称为A与B的和(差)，记为C=A±B.

定义6[6]矩阵的数量乘法:设A=(aij)mn,是m×n矩阵，λ是一个常数，则λ(aij)mn=(λaij)mn称为矩阵A=(aij)mn与数λ的数量乘积，记为λA.

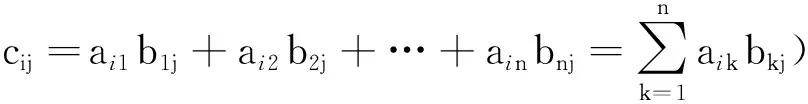
定义8[4]把一矩阵A的行列互换，所得到的矩阵称为A的转置，记为A′或者AT.

定义9[7]如果n阶方阵A满足AT=A，则称矩阵A为对称方阵，这时aij=aji.

定义10[7]如果n阶方阵A满足AT=-A，则称矩阵A为反对称方阵，这时aij=-aji.

定义11[6]在行列式

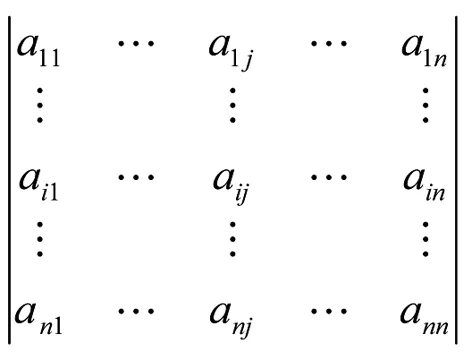
中划去元素aij所在的第i行与第j列，剩下的(n-1)2个元素按原来的排法构成一个n-1 级的行列式称为元素aij的余子式，记为Mij，再把Aij=(-1)i+jMij称为代数余子式.

定义12[4]设Aij是矩阵 (aij)mn中元素aij的代数余子式，矩阵

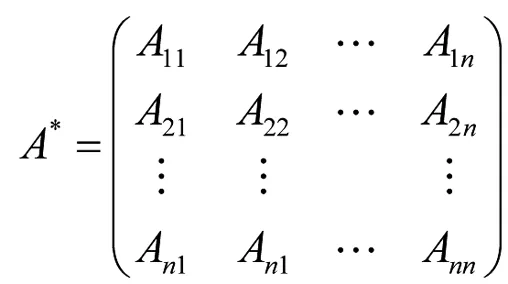
称为A的伴随矩阵.

定义13[4]数域P上的n×n矩阵A如果

|A|≠0，称为矩阵A是非退化的.

1.2 K-复数的相关引理

引理1[5]z1+z2=(x1+y1i)±(x2+y2i)=(x1±x2)+(y1±y2)i.

引理2[8]λz=λ(x+yi)=λx1+λyi.

引理3[9]z1×z2=(x1+y1i)×(x2+y2i)=(x1x2-y1y2)+(x1y2±x2y1)i.

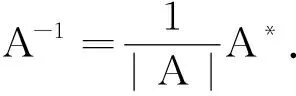
2 K-复数的运算和矩阵运算的关系

2.1 K-复数的基本运算

K-复数的矩阵表示打破了一直以来复数的代数表示、几何表示、指数表示的数学思维，K-复数的基本运算也可以通过矩阵的基本运算来完成.

(1)K-复数的加法与减法运算

二阶矩阵之间的加(减)法运算是封闭的，于是集合V中的任意两个矩阵可以做加(减)法运算，所得到的和(差)仍在集合V中.

定理1 任意两个K-复数z1(k)、z2(k)相加(减)所得到的K-复数z(k)可唯一构造一个K-矩阵M(k)，则该K-矩阵M(k)等于K-复数z1(k)、z2(k)所构造的K-矩阵M1(k)、M2(k)相加(减)，即

ρ:(z1(k)±z2(k))→M1(k)±M2(k)

(1)

证明设

z1(k)=a1+kb1i,z2(k)=a2+kb2i.

根据定义4可得

根据引理1可得

z(k)=z1(k)±z2(k)=(a1±a2)+

(kb1i±kb2i)=(a1±a2)+k(b1±b2)i,

所以

再根据定义5可得

M1(k)±M2(k)=

所以M(k)=M1(k)±M2(k),

即

ρ:(z1(k)±z2(k))→M1(k)±M2(k).

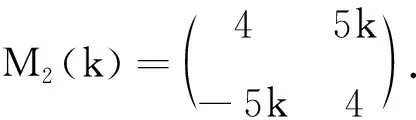
求: (1)z1(k)+z2(k) 的K-矩阵；

(2)z1(k)-z2(k)的K-矩阵.

解因为

所以根据式(1)得

(2)K-复数的数量乘法运算

定理2 任意实数λ与任意K-复数z(k)相乘所得到的K-复数z′(k)可唯一构造一个

K-矩阵M′(k)，其中M′(k)=λM(k)，即

ρ:(λz(k))=λ[ρ:z(k)]→λM(k)

(2)

证明设

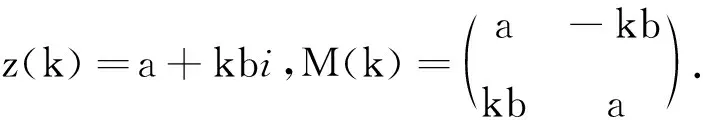
根据引理2可得

z′(k)=λz(k)=λa+λkbi,

所以

根据定义6可得

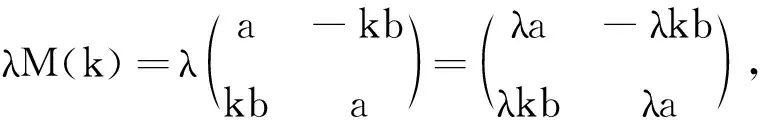
所以

M′(k)=λM(k),

即

ρ:(kz(k))=λ[ρ:z(k)]→λM(k).

例2 设z(k)=2+3ki，求λz(k)的K-

矩阵.

所以根据式(2)得λz(k)的K-矩阵为:

(3)K-复数的乘法运算

定理3 任意两个K-复数z1(k)、z2(k)相乘所得到的K-复数z(k)可唯一构造一个K-矩阵M(k)，该K-矩阵M(k)等于K-复数z1(k)、z2(k)所构造的K-矩阵M1(k)、M2(k)相乘，即

ρ:(z1(k)×z2(k))→M1(k)×M2(k)

(3)

证明设

z1(k)=a1+kb1i,z2(k)=a2+kb2i.

根据定义4可得

根据引理3可得

z(k)=z1(k)×z2(k)=(a1+kb1i)×(a2+kb2i)=(a1a2-k2b1b2)+k(a1b2+a2b1)i,

所以

根据定义7可得

所以

M(k)=M1(k)×M2(k),

即

ρ:(z1(k)×z2(k))→M1(k)×M2(k) .

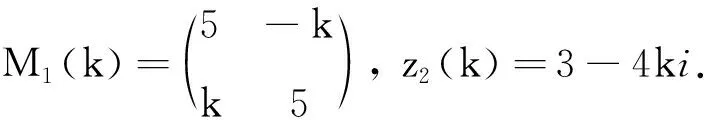
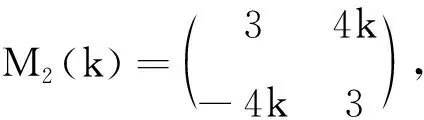
(4)K-矩阵的转置与共轭K-复数

(4)

证明设

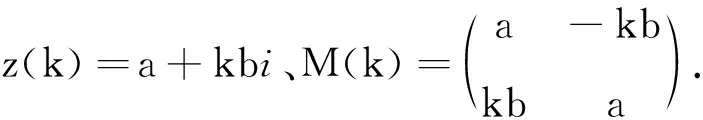
根据定义2可得

根据定义4可得

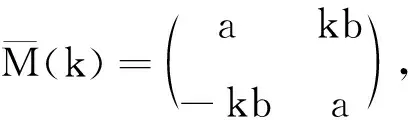
再根据定义8可得

所以

即

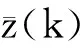
矩阵.

解根据定义4可得

根据定义8可得

再根据公式(4)

(5)对称方阵、反对称方阵与K-矩阵的关系.

定理5对任意K-复数z(k)=a+kbi，当a=0、b=0时，z(k)=0所构造的K-矩阵既是对称方阵又是反对称方阵.

证明设

根据定义8可得

所以

MT(k)=M(k)=-M(k).

则M(k)既是对称方阵又是反对称方阵.

(6)伴随矩阵与K-矩阵的关系

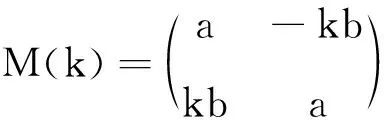
ρ:(z(k))→M(k)=M*(k) .

(5)

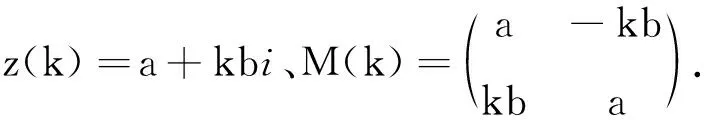
根据定义11可得

A11=a、A12=kb、A21=-kb、A22=a,

再根据定义12可得

所以

M(k)=M*(k),

即

ρ:(z(k))→M(k)=M*(k).

例5 设z(k)=3-7ki，求M*(k).

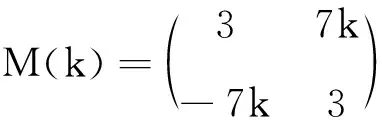
根据公式(5)可得

(7)可逆矩阵与K-矩阵的关系

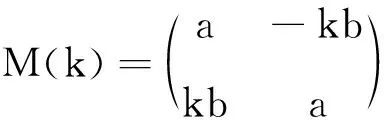
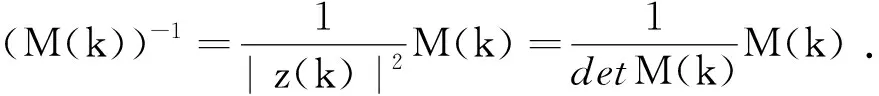
(6)

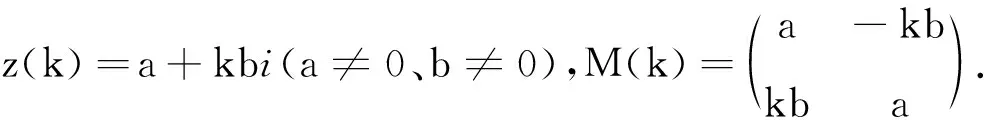
由定义13可得，当a≠0、b≠0时，z(k)=a+kbi的K-矩阵是非退化的，

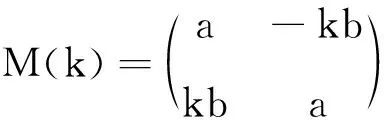
由引理4可得

所以

例6 设z(k)=3+7ki，求M-1(k).

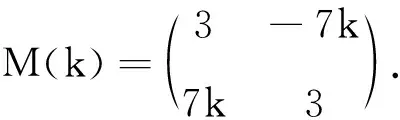
再根据公式(6)

可得

3 结论

通过研究K-复数的矩阵表示、K-复数的矩阵表示的基本运算与矩阵的基本运算之间的关系，以及矩阵的其它运算在K-复数上的应用.熟悉掌握K-复数的矩阵表示，能够灵活运用K-复数的矩阵表示及其相关性质来解决数学问题.K-复数的矩阵表示不仅让复数的表示方法多样化，而且还把复数与矩阵的性质紧密结合起来，对于解决K-复数的数学问题具有极大的参考作用.