基于改进遗传算法的AGV路径规划

孙 波，姜 平+，周根荣，董殿永

(1.南通大学 电气工程学院，江苏 南通 226019；2.南通大学 图书馆，江苏 南通 226019)

0 引 言

随着自动引导运输车(automated guided vehicle，AGV)[1]在工业生产中的广泛应用，其路径规划也成为目前的热点问题之一。路径规划算法主要有传统算法(如Dijkstra算法[2,3]、A*算法[4,5])和智能优化算法(如蚁群算法[6,7]、粒子群算法[8]和遗传算法[9-12]等)之分。由于遗传算法具有较好的并行性和鲁棒性，被广泛应用于AGV路径规划中，但算法本身却有早熟收敛和局部搜索能力较弱等缺点。针对遗传算法的这些缺点，已经有不少的改进方案被提出，如文献[9]提出了一种将障碍物凸化处理的地图模型建立法，方便了遗传算法的初始种群生成；文献[10]对自适应算子进行新的修改，提高了算法初期进化的能力；文献[11]提出了一种结合禁忌搜索算法的初始种群生成方法；文献[12]提出了一种多次随机交叉法来维持种群的多样性。虽然上面的各种改进操作提升了遗传算法的部分性能，但是算法仍然存在一些缺点需要优化：首先，算法的选择操作并没有实质性的改进；其次，算法的设计没有结合实际运行环境。

本文结合AGV路径规划的特点，对基本遗传算法进行了相关改进操作，首先将模拟退火思想引入到算法的种群选择操作中，并对交叉、变异的方法进行改进优化，增加了种群中个体的差异性，让算法可以更好跳出局部最优解。此外，在建立适应度函数时，引入路径曲折度、繁忙度和车辆负重度等规划指标，使得规划出来的路径更符合实际情况。

1 环境模型的建立

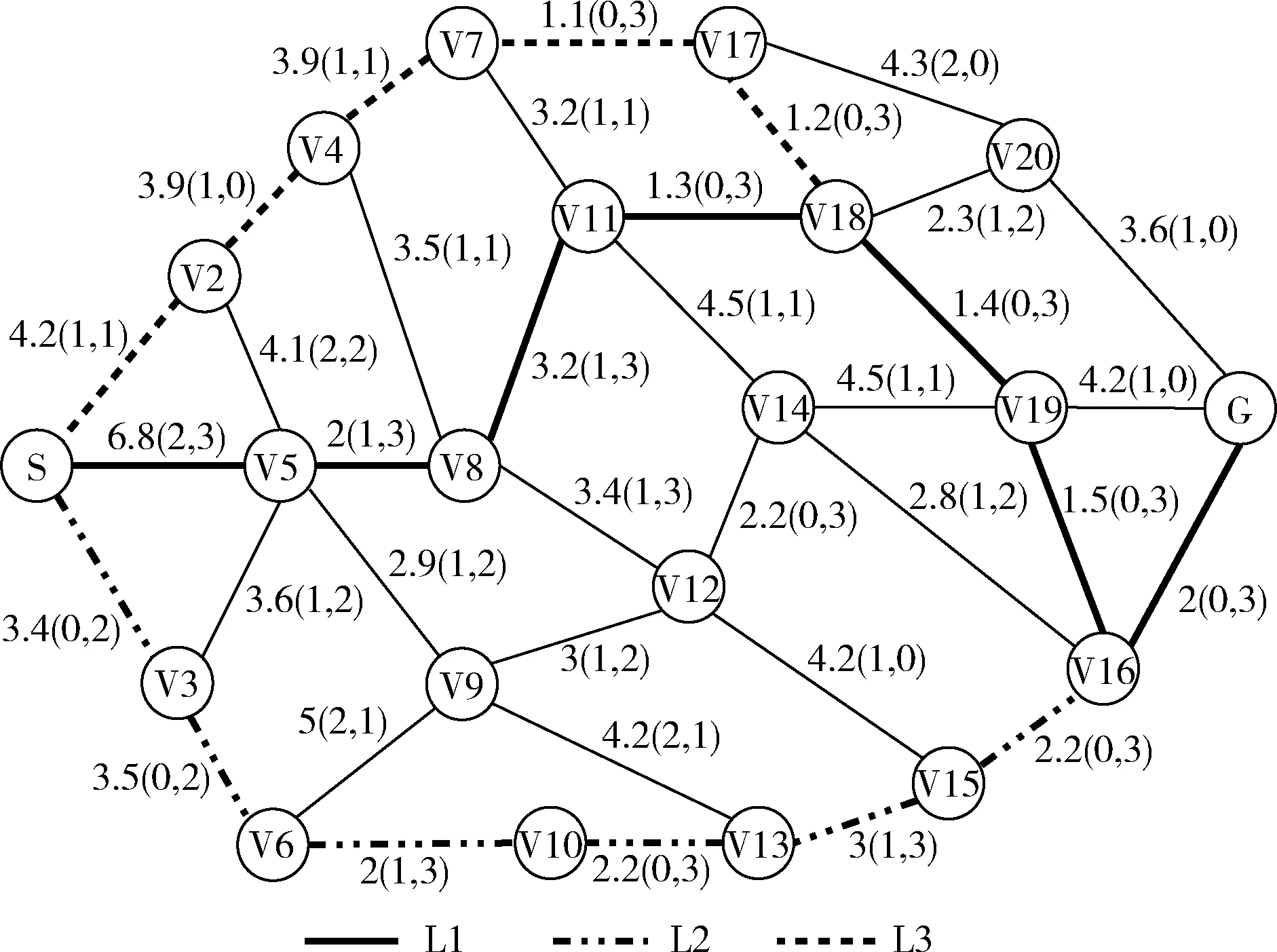
在路径规划前，首先要对AGV的运行环境进行合理的地图建模，本文采用拓扑地图法对AGV的运行空间进行环境建模。图1为本文采用的地图模型，其中S，V2，…，V20，G等称为节点，表示实际工厂中的AGV工作站；节点之间的数据称为路径权值，表示AGV行走路径的相关信息，采用Dis(α,β) 的形式表示，其中Dis为两节点间的实际距离，α表示路径的曲折度等级(最大为10级)，β表示路径的繁忙度等级(最大为10级)；S为路径规划起始点，G为路径规划的目标点。

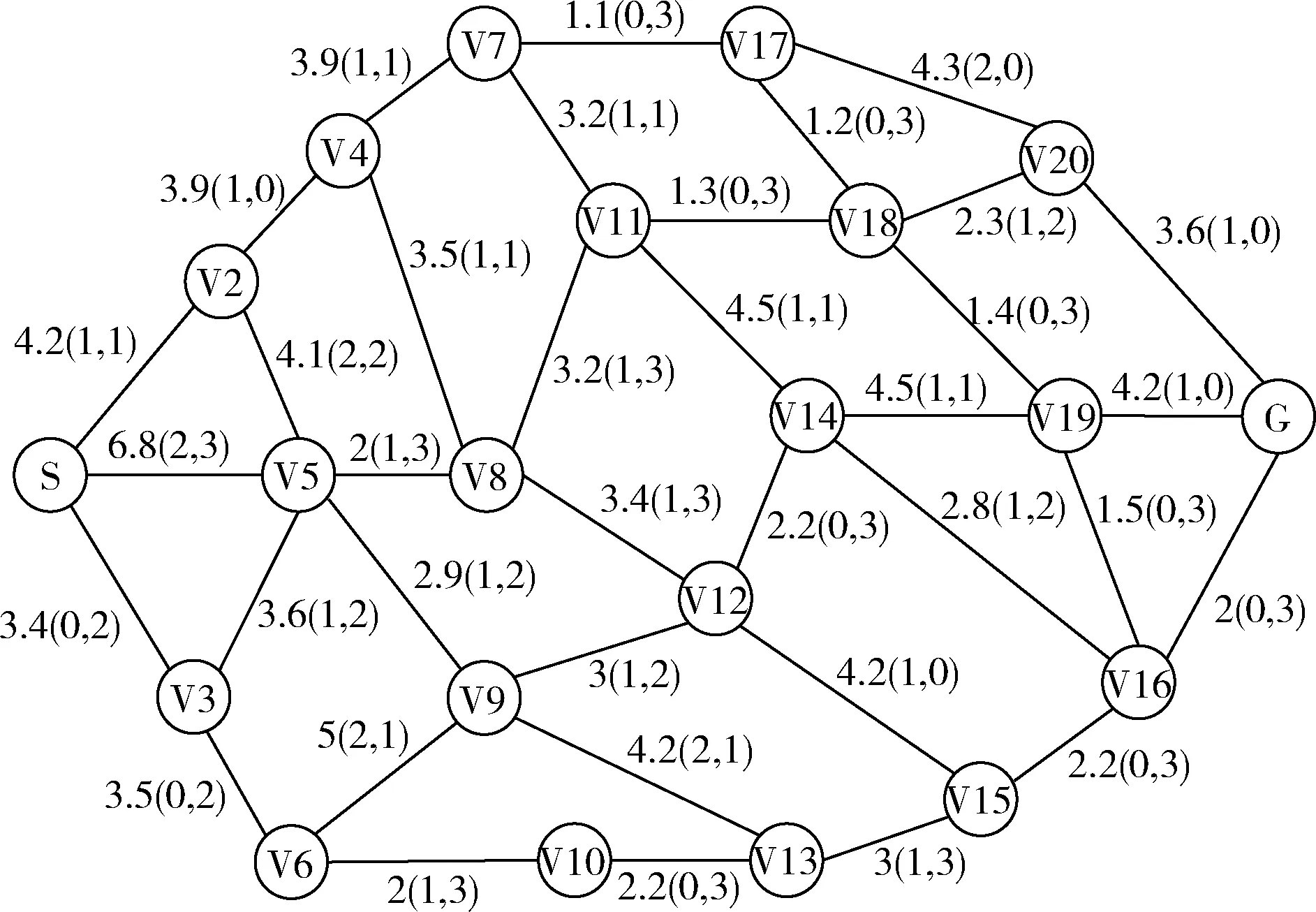
图1 AGV路径规划地图模型

2 路径规划算法

2.1 编码方式

在AGV的路径规划中，可以将AGV自起始点到目标点的运行路径作为遗传算法中的一条染色体。由于本文的环境模型为拓扑地图模型，故采用变长度的符号编码方式[13]，将地图模型中的节点号对应于染色体中的基因，当然相邻的基因必须是地图中的相连节点。如图1中，一条可行路径可以表示为：S→V5→V8→V12→V14→V19→G。

2.2 适应度函数

为提高AGV在运行过程中的安全性，减少AGV间或AGV与障碍物间碰撞的发生，本文引入AGV负重度、路径曲折度和路径繁忙度等规划指标，对AGV的运行速度进行如下制约

(1)

其中，Vt为小车在无规划指标下的运行速度(本文默认为0.5 m/s)，μ为AGV的负重系数(1≤μ≤2，无负载时为1，满负载时为2)，α为路径曲折度等级(等级数为1-10级，等级数越大，路径越曲折)，β为路径繁忙度等级(等级数为1-10级，等级数越大，路径中可能同时存在的车辆数越多)，D为最大等级数(本文取10)。

本文把路径规划的评价依据设定为AGV从起始点行驶到目标点所花费的时间，在车辆负重度、路径曲折度和路径繁忙度等规划指标下，结合式(1)，可得适应度函数为

(2)

式中：Dis(Xij) 为个体Mt中节点i和节点j之间的路径长度，μij为AGV在该段路径中的负重系数，αij为该段路径的曲折度等级，βij为该段路径的繁忙度等级，D为最大等级数。从式(2)中可以看出：规划出的最优路径对应的适应度函数值也将最小。

2.3 初始种群

在初始种群的产生过程中，生成的个体不能存在断路和环路状况，并且初始种群中，应该尽量避免重复的个体产生，初始种群的具体产生步骤如下：

(1)将起始点S放在集合C中；

(2)随机选取与起始点相连的一个节点按顺序放在集合C中；

(3)判断集合C中最后一个节点是否为目标点，如果是则执行步骤(7)，否则执行步骤(4)；

(4)取出与集合C最后一个节点相连的所有节点于集合N中；

(5)去掉集合N中与集合C重复的节点；

(6)随机选取集合N中的一个节点按顺序放在集合C中，执行步骤(3)进行判断；

(7)判断种群中与本个体重复个体数量，如果重复个体少于2个，则本个体生成成功(即为集合C内容)，执行步骤(8)，否则执行步骤(1)，重新生成一个新个体；

(8)判断是否达到种群规模，如果达到种群规模则初始种群生成成功，否则执行步骤(1)，进行新一轮的个体产生。

2.4 遗传操作

2.4.1 选择操作

由于轮盘赌选择方式会使后代产生的个数与父代个体的适应度大小成正比，容易造成“早熟”现象[14]。为了兼顾种群的多样性和避免优秀个体被破坏，在进行选择操作时，不采用传统的轮盘赌选择法，改引用模拟退火算法的选择思想进行种群选择，然后对新产生的种群执行改进后的精英保留策略，即按一定比例淘汰种群中较差个体，同时复制一些优秀个体并使它们不经过交叉和变异操作而直接保留到下一代，以保证种群个体的合理性。

模拟退火算法来源于固体的物理退火原理，给定固体一个较高的初始温度，让其按一定的降温速率衰减，在降温过程中结合概率选择特性，在解空间中寻找最优解，直到温度降到设定的最低温度时退火结束。模拟退火操作主要采用式(3)的形式来确定算法产生新解的接收概率，由于其可以很好跳出局部最优，被广泛地应用于其它算法的改进工作之中[15]

(3)

式中：f(m)、f(n) 分别为进化前和进化后的适应度函数值，T为系统的当前温度值，并随时间衰减。其计算公式如下

T=T0×qt

(4)

式中：T0、q和t分别为系统的起始温度、降温速率和迭代的次数。

2.4.2 交叉操作

交叉操作采用单点交叉法，具体步骤如下：

(1)取出父代个体V1和V2中除起始点和目标点外的共同节点于集合Nc中，如果集合Nc非空则执行下一步，否则执行第(5)步；

(2)任选集合Nc中一节点i作为交叉点；

至此，矩阵Φ中的每个向量都是非标准正交的，需使这些向量除以对应的得到标准正交基函数{φ1,φ2,…,φN}，即POD模态。将瞬态速度场投影到POD基函数上，求出各模态的系数。通过计算得到所有POD模态及对应的模态系数，可线性重构任意时刻的速度场，有

(3)对V1和V2执行关于i节点的交叉操作，其过程如图2所示；

(4)判断交叉后的两个子个体中节点i前后是否存在相同节点，如果不存在则本次交叉完成，否则执行下一步；

(5)若两个父代个体没有交叉点或交叉操作生成的新个体不是一个完整的路径，则认为本次交叉失败，此时将父代个体中较优的一个作为子个体1，而子个体2则重新生成。

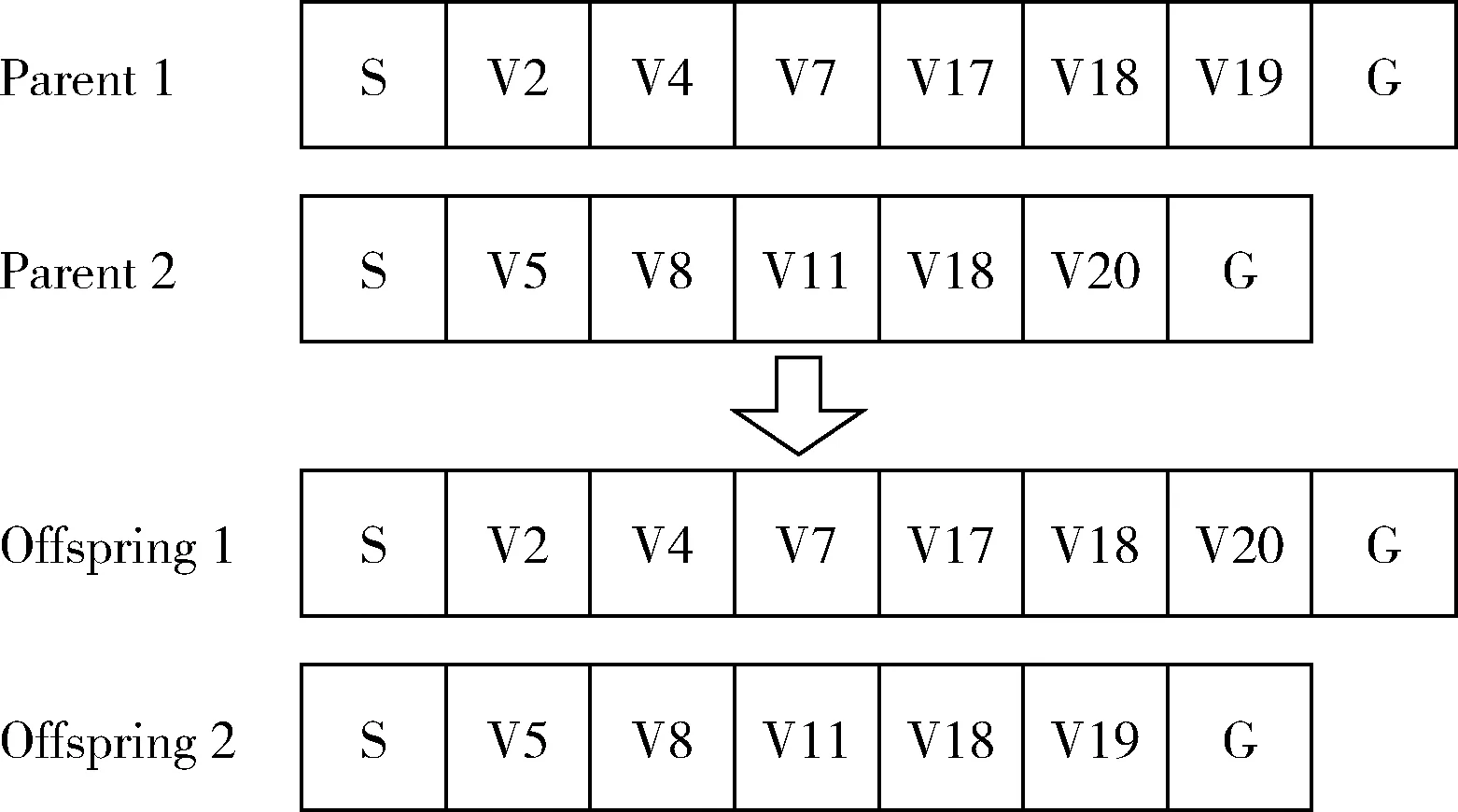
图2 交叉操作

2.4.3 变异操作

变异操作的具体过程为：

(1)从待变异父个体V中随机选取一个节点i(不包括起始点和目标点)作为变异节点，将父个体V分成两条路径r1和r2；

(2)按类似于初始种群产生的方法生成两条路径，一条为从起始点S到节点i的路径R1(要求R1中不包含r2的其它节点)，一条为从节点i到目标点G的路径R2(要求R2中不包括r1的其它节点)；

(3)若步骤(2)可以实现，则将R1和r2，r1和R2组成两个新的个体，否则执行步骤(5)；

(4)计算步骤(3)产生的两个个体的适应度函数，选取较优的一个个体作为变异操作产生的子个体，变异操作完成，如图3所示；

(5)生成的子个体存在断路或环路情况，视为变异操作失败，按交叉失败中子个体2产生法重新生成一个新个体。

图3 变异操作过程

2.4.4 交叉和变异算子自适应调整

在遗传算法中，算法的收敛速度和搜索结果很大情况下会受到交叉概率Pc和变异概率Pm的影响。如果交叉概率Pc较大，则可以很快地产生新个体，但适应度较高的个体可能会被破坏，若Pc值取的较小，则会拖慢系统的进化速度；如果变异概率Pm的取值太大，则不利于算法的收敛，Pm取的值太小，则新个体的产生困难，种群多样性变差[16]。在文献[17]中Srinvivas等提出一种自适应遗传算法，其表达式如下

(5)

(6)

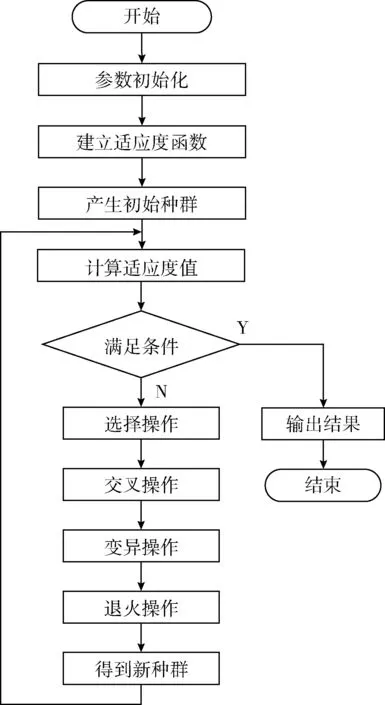
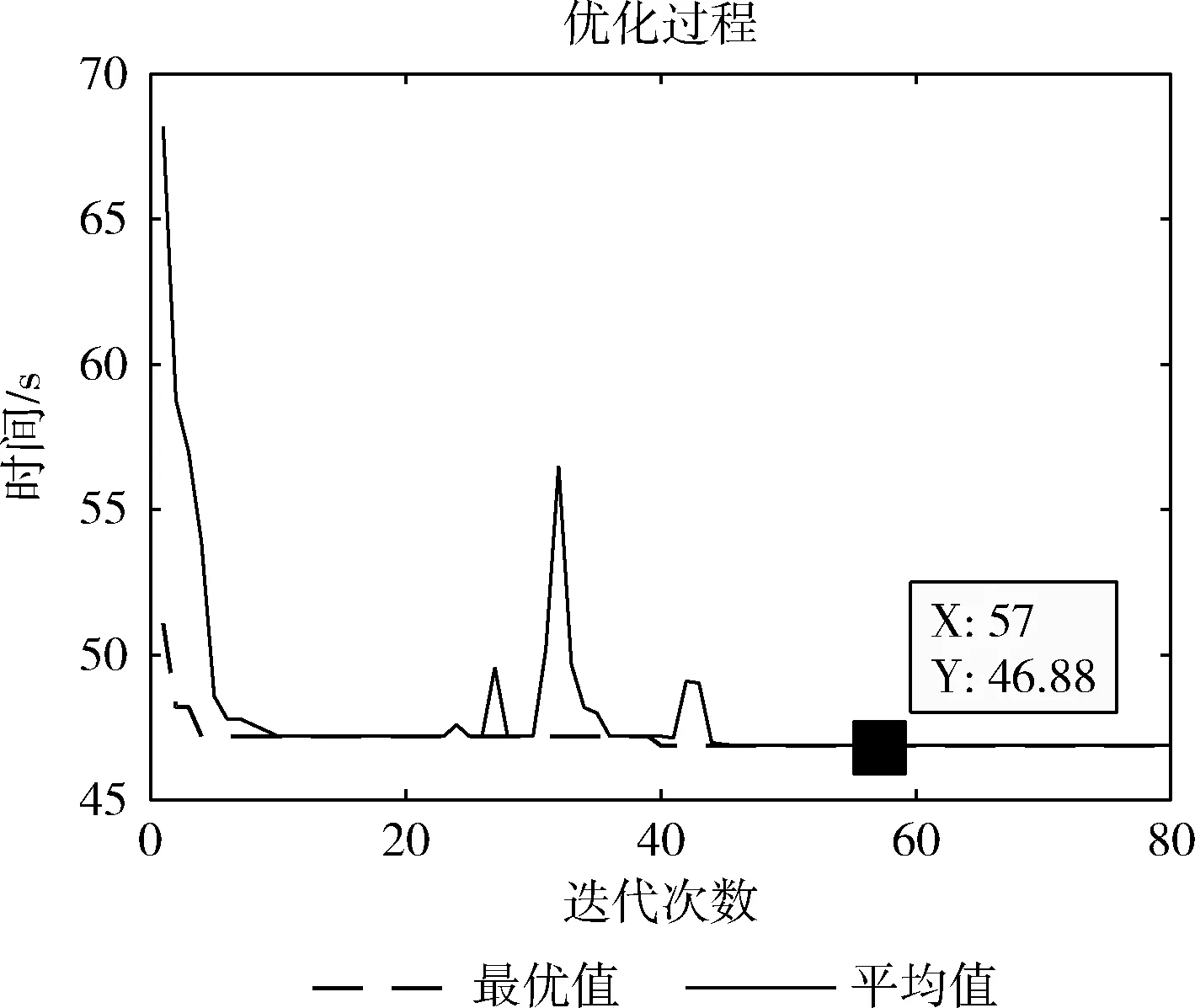
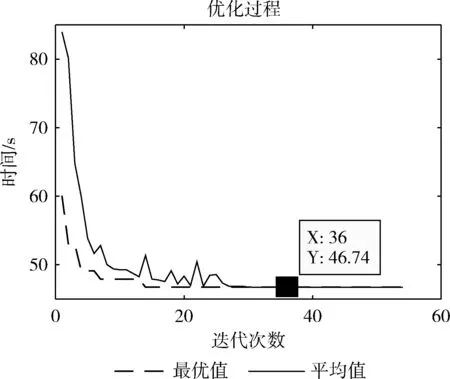
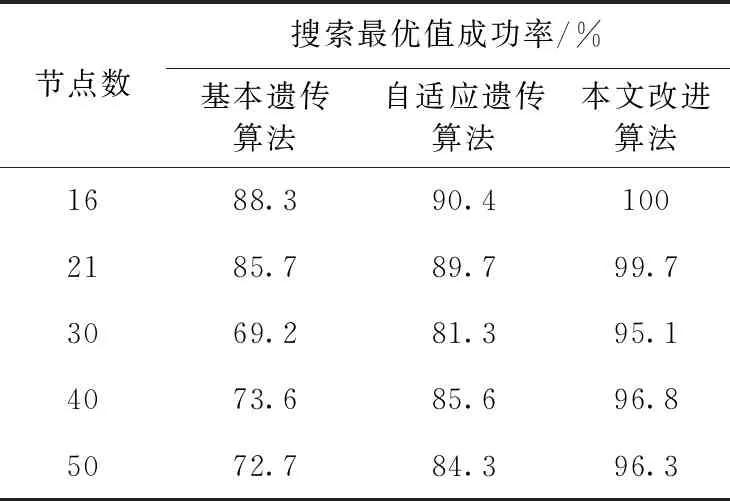
式中： 0

从公式分析中可以看出，这种调节方法不利于进化初期时种群中较优个体的变化，容易导致进化出现早熟收敛现象，又加上该调整方式是针对求最大适应度值的方法，所以按式(7)和式(8)进行修改，使种群中最小适应度的个体的交叉变异率不为0，分别提高到了Pc2和Pm2，提高了种群中较优个体的交叉概率和变异概率，加快了进化的进行[18]

(7)

(8)

式中：fmin、favg、f′、f分别为最小适应度值、平均适应度值、交叉操作中小的适应度值以及变异个体的适应度值，由于在种群选择中采用了模拟退火法的选择操作和改进后的精英保留策略，所以这里的交叉、变异概率可以取较大值，Pc1=0.9，Pc2=0.6，Pm1=0.3，Pm2=0.1。

2.5 算法流程图

算法流程图如图4所示，算法的终止条件为：最优解在连续40次的进化中都没有改变或进化的次数达到系统预设的上限。式(4)所示的为系统最大的进化次数计算公式

(9)

式中：T0为初始温度，q为降温速率，Tend为终止温度。在本文中，取初始温度T0=5000℃，终止温度Tend=0.0005℃，降温速率q=0.9，则最大进化次数tmax=153。

图4 算法流程

3 仿真结果分析

3.1 仿真结果对比

采用MATLAB软件对图1所示的地图模型进行路径规划的编程验证，适应度函数为式(2)，运行速度Vt=0.5 m/s，负重系数μ=1。为增加合理性对比验证，分别对基本遗传算法、自适应遗传算法和本文改进遗传算法进行多次实验，最后用Dijkstra算法规划出最短路径进行实际验证，得最优路径为：S→V2→V4→V7→V17→V18→V19→V16→G，适应度函数值为46.74 s。

在基本遗传算法中，种群规模、交叉概率和变异概率分别选择为：M=10、Pc=0.6、Pm=0.1，选择方式为轮盘赌选择，终止条件为进化次数达到tmax或连续40代最优解不变，找到的最优路径为：S→V3→V6→V10→V13→V15→V16→G，进化曲线如图5所示。

图5 基本遗传算法进化曲线

自适应遗传算法在基本遗传算法的基础上按式(7)、式(8)进行交叉和变异概率自整定，为保证优良个体不被破坏，加入改进后精英保留策略，其它条件不变，找到的最优路径为：S→V2→V4→V7→V17→V18→V19→G，进化曲线如图6所示。

图6 自适应遗传算法最优解进化曲线

本文改进遗传算法在自适应遗传算法的基础上引入模拟退火的选择思想，退火参数如式(9)中所示，其它条件不变，得到最优路径为：S→V2→V4→V7→V17→V18→V19→V16→G，进化曲线如图7所示。

图7 改进遗传模拟退火算法最优解进化曲线

从图5到图7可以看出，平均值曲线波动越大，说明种群的差异性越大，算法跳出局部最优解的可能性就越大。最优解收敛速度越快，说明算法的执行效率越高。基本遗传算法不仅种群差异性非常小，算法收敛的速度也非常慢，并且因为没有应用精英策略，导致种群中的优良个体遭到破坏，使算法陷入局部最优，不利于算法的运行。自适应遗传算法相较于基本遗传算法，种群差异性和算法的收敛速度都有明显改善，但是由于轮盘赌的选择方式会使后代产生的个数与父代个体的适应度大小成正比，导致种群中个体的多样性被破坏，容易造成“早熟”现象。本文改进的遗传算法采用Metrolpis接收准则来接收交叉、变异后的新解，所以种群中不同个体的数量比较多，易跳出局部最优解。如图7所示，即使初始产生的最优解不是很好(比图5、图6的初始最优解都要差)，但是由于种群差异性大，算法也可以很快找到最优解。

为验证本算法的通用性，把本算法应用于5种不同的自制地图，每张地图各进行1000次仿真，为对比本文改进算法的有效性，分别与基本遗传算法，自适应遗传算法(加入精英保留策略)进行平均搜索速度和搜索成功率的比较。对比结果见表1和表2。

表1 平均搜索时间对比

5张自制地图信息如下：地图1有16个节点，24条路径；地图2即为本文地图，21个节点，36条路径；地图3有30个节点，55条路径；地图4有40个节点，77条路径；

表2 3种算法的搜索成功率对比

地图5有50个节点，102条路径。对于算法的相关参数，除种群规模改为20外，其它参数保持不变。

从表1和表2中可以看出：随着节点数的增加，改进遗传算法的搜索速度和搜索成功率比基本遗传算法和传统自适应遗传算都有很大的提高。在地图3的设计上，故意设计了多条干扰路径，但本算法仍能较为准确地规划出最优路径，改进后的算法在实际应用中有很好的通用性。

3.2 不同指标下的规划结果

图8所示的分别是：在AGV小车速度Vt=0.5 m/s，负重系数μ=1的情况下，不考虑路径曲折度和繁忙度规划出的路径L1，路径为：S→V5→V8→V11→V18→V19→V16→G；只将路径曲折度作为规划指标规划出来的路径L2，路径为：S→V3→V6→V10→V13→V15→V16→G；路径曲折度和繁忙度都作为规划指标规划出来的路径L3，路径为：S→V2→V4→V7→V17→V18→V19→V16→G。

图8 不同规划指标下的最优路径

3条路径在不同指标参数下的适应度值见表3。从图8和表3中我们可以看出：在不同参数下，本文改进后的遗传算法均能正确规划出系统的最优路径；在路径规划过程中需考虑到诸多环境因素，这样规划出的路径才更高效，也更贴近实际情况，如表3中，无规划指标，一个规划指标和两个规划指标规划出的路径是不同的，虽然AGV负重系数μ的改变不会影响规划出路径的结果，但可以较为准确的规划出AGV从起始点到目标点的运行时间，这样对多AGV系统的调用，输送系统的时间规划都有非常重要的意义。

表3 3条路径在不同规划指标下的适应度值

4 结束语

针对AGV在路径规划存在的问题，对自适应遗传算法进行相关修改优化，在多次实验对比验证后，表明了本算法在AGV路径规划方面的应用是高效的。其主要特点如下：

(1)对交叉、变异方法进行相关改进，提高了种群中新个体的产生能力，加大了种群个体的差异性。

(2)对自适应交叉、变异算子进行改进，同时将精英保留策略应用于选择操作中，提高了算法的求解效率。

(3)引入模拟退火思想，使得初期种群个体差异性大，易于跳出局部最优解。

(4)适应度函数中引入路径曲折度、路径繁忙度以及车辆负重度等评价指标，使得规划出的最优路径更安全可靠、更切合实际。

本算法若要实际应用到工业生产中，还需考虑一些问题：首先是搜索速度和稳定性，仍有待提高；其次是本算法只是静态路径规划，对AGV运行过程中的突发情况没有考虑，所以静态和动态的组合路径规划也是进一步的研究方向。