高中数学函数解题思路多元化的方法举例分析
李 皓
(广东省珠海市斗门区第一中学 519100)
一、高中数学函数的学习误区
在高考中,数学占据很高的分值,也是拉分的重要科目之一,故而高中生及教师均给予数学学科较高重视.但是纵观全局,多数高中生在数学考试中取得高分,还有部分学生在数学知识学习中投入较多时间与精力,但是结果不甚理想.究其成因,最根本的是学生对数学学习方法的认识上存在偏差,特别是在解题思路上.很多学生片面地认为,只有通过“题海战术”才能完善函数解题思路.这不仅能加重学生的压力,也会削弱他们学习的积极性,最终造成他们长期不能突破瓶颈,仅能取得基础分数.
二、高中数学函数解题思路多元化的意义分析
函数课程教学实质上是探究因变量和自变量之间的关系,并以不同的基本条件为基础,联系数学理论而应用于现实问题中的一种方法.可以把解题思路细化为“审题→联想→思考→解题”,审题是了解题目内容,并以问题为基础在理论层面上进行拓展;联想即分析数学理论和函数性质间的相关性;思考是建立已知与未知条件的关系,并明确题目限制条件的内容后进行有效排除;最后是联合使用各种条件,并以基础公式等为支撑,解决问题,特殊情况下需关联图象与函数之间的关系.
三、高中数学函数解题思路多元化的举例
1.发散性思维
数学属于一门抽象性很强的学科,学生通常采用演练大量习题的形式掌握知识点.但是,在课时与课本资源不充足等条件的约束下,部分教师讲解数学习题时,多是只讲一种解题方法,或学生通过教材掌握一种单一的解题方法.这样的教学模式,学生会处于被动解题的状态中,思维的深度与广度不能实现有效拓展,知识整合效果整体偏低.为解除以上现状,教师在讲解函数习题时,应尽量做到“一题多解”,进而协助学生能从不同角度去了解函数思想,积极和具体问题相结合去处理问题.
比如,在《导数在研究函数中的应用》课程教学中,教师组织学生共同探究“用导数求函数的单调区间有哪几个步骤”的问题.学生1:第一步,求函数导数;第二步,建立导函数不等式,使f(x)>0的区间为原函数的增区间,使f(x)<0的区间为函数的减区间;第三步,回答单调区间.并组织学生以小组合作学习的形式解答如下问题:求函数f(x)=x2eax的单调区间.有学生作出如下解答过程:
函数的定义域为R.对函数求导f′(x)=2xeax+ax2eax=eax(ax2+2x).
当a=0时,函数的单调增区间为(0,+∞),函数的单调减区间为(-∞,0);
当a>0时,函数的单调增区间为(-∞,-2/a)和(0,+∞),函数的单调减区间为(-2/a,0);
当a<0时,函数的单调增区间为(0,-2/a),函数的单调减区间为(-∞,0)和(-2/a,+∞).
2.创新性思维
在高中函数课程教学中,教师要实时将创新思维的培养融合其中,尝试采用新的解题方法解答函数问题,引导学生在不断练习中逐渐突破重难点,并积极使用多元化方法及不同知识点优化解决问题.为达成以上教学目标,就要求教师在实践中积极对与函数问题相关的理论知识进行整合讲解,引导学生采用不同思路去处理问题.
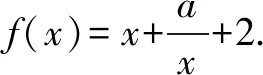
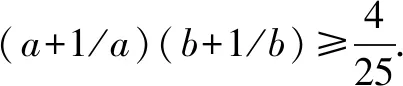

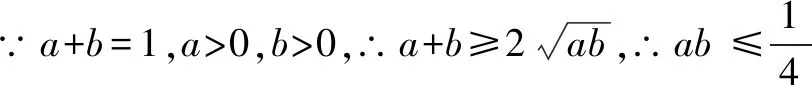
3.逆向思维
即在高中函数课程教学中,教师依照个体思维方向的不同,依照题目中出示的线索探寻答案,这是正向思维,而若依照题目中给定的要求,假设其成立,继而循序渐进推导中题目中已知条件,则该种解题思维被称之为逆向思维.正向、逆向思维是一题两面、密切相关、相辅相成的.
总之,学生在解答函数问题过程中,教师应加强对其函数多元化解题思维及思路的引导,并以现实问题为基础,突破常规思维的局限性,协助学生在不断练习的过程中能扭转传统固有的解题思路,实现对数学函数解题思维模式的有效开发,提升自身的学科素养.

