基于田口法定子冲片优化研究

邱瑞林，华青松，史成龙

（青岛大学 机电工程学院，青岛266071）

0 引 言

永磁同步电机由于采用稀土永磁材料代替了传统电机的励磁绕组，具有无滑环和电刷结构、噪声低、输出转矩高、效率高等优点［1］，因此被广泛应用在新能源汽车、航空航天、医疗等领域。转速超过10 000r／min的电机即可定义为高速电机，高速电机和普通的低速电机相比，在相同输出功率的条件下，具有电机尺寸较小、占用空间小、电机功率密度较高的优点。但是在高速运行下，电机的转矩脉动会增大电机的振动和噪声，影响电机的使用寿命，同时更高的电磁场交变频率也带来了更高的定子铁耗和电机温升过高的风险，降低电机的输出效率［2］。因此，在高速永磁同步电机设计和优化过程中，需要考虑对电机的转矩脉动、齿槽转矩和定子铁耗优化，以期达到减小高速运行时的噪声和振动、提高电机效率的目的［3］。大量文献对永磁同步电机转子进行优化设计，但鲜有对定子铁心进行优化设计的研究。文献［4］给出了永磁同步电机定子齿宽度和定子轭部厚度与磁密的关系，并给出了计算定子铁耗的理论计算公式。文献［5］提出了一种基于遗传算法的定子齿形优化方法。文献［6］采用田口算法对电机的转子结构进行优化。

本文对一款额定功率10kW，额定转速40 000 r／min的表贴式内转子永磁同步电机定子冲片进行优化研究。以往对永磁同步电机的优化都是选取电机一个或多个需要优化的参数，针对不同的参数点进行有限元仿真，依据仿真结果选取最优的参数组合，该方法操作简便，只需对仿真结果进行比较，即可选出最优的参数组合。但是该方法需要的仿真时间过长，效率比较低，而且仿真了大量无用结果，浪费了大量计算机内存资源。

田口法是日本著名的质量管理专家田口玄一提出的，它原本是应用于产品质量管理工程的方法［7］。田口法采用正交化实验的方法，在需要优化的参数中选取几个不同的水平数，设计正交实验表，对产品依据正交实验表进行实验，将实验结果中不同因子的实验结果分离出来，经过数据处理，得到不同因子对优化参数的作用程度，选取并验证最优的参数水平组合。

表贴式永磁同步电机定子结构中，定子槽的形状是影响电机性能的重要因素，本文以定子槽口高度、定子槽口宽度、定子槽高度为优化参数，以降低转矩脉动、齿槽转矩和定子铁耗为优化目标，以电机输出扭矩满足最高转速时输出扭矩为基本要求，通过ANSYS Electronics Desktop有限元仿真软件进行仿真实验，将实验参数通过田口法优化后，比较电机在优化前后的性能变化，研究田口法对定子冲片优化的效果。

1 永磁同步电机模型和参数

本文优化的对象为一款24槽4极表贴式内转子永磁同步电机，电机的结构尺寸如表1所示，结构如图1所示。

表1 永磁同步电机基本结构参数

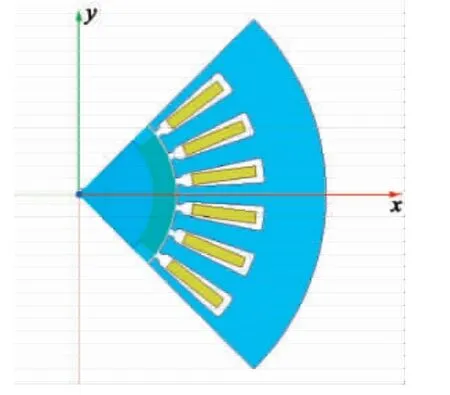
图1 表贴式永磁同步电机结构示意图

在永磁同步电机中，定子槽的形状尺寸在电机设计中有着重要的地位，影响着最终的整机性能。图2为定子槽型参数示意图，其参数分别是定子槽口宽度bs0、定子槽口高度hs0、定子槽楔高度hs1和定子槽高度hs2。

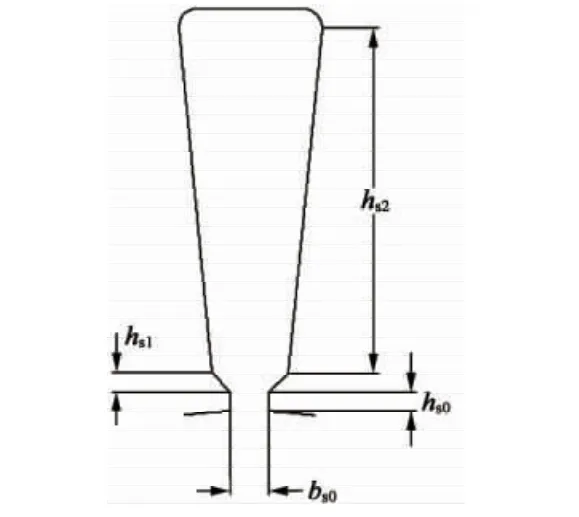
图2 定子槽型参数示意图

2 基于田口法的定子冲片优化

田口法将不同因子建立正交组合，使实验结果具有均匀统一的特点。虽然田口法是一种局部优化实验，但仍具有代表性，而且其优化的过程能够大大减少实验次数［8］。采用田口法能够缩短优化所需要的时间，加快电机电磁设计的优化速度。

田口法正交实验由以下部分组成：

1）确定可能影响电机性能的优化因子，确定电机最优方案可能的水平，确定预计的优化目标；

2）建立不同优化因子与不同水平组成的正交表，并对正交表中不同的实验进行电磁有限元仿真；

3）利用平均值和方差对不同的实验结果进行分析，分离出不同因子对实验结果的影响程度，选择最优的实验参数组合［9］。

电机壳体在设计时需要考虑电机外壳尺寸的限制、冷却散热接触面积的要求，电机转子在设计时需要考虑护套的强度、转子动力学的性能要求。如需对电机壳体和转子进行改动，设计周期过长，时间成本高。本文仅考虑在定子内、外径不变的情况下，对定子冲片进行优化研究。对不同的优化因子选取了5个不同的水平取值，表2即为不同优化因子与不同水平正交表，其中考虑到定子槽满率的要求，希望不改变绕组的接线方式，这样对电机绕组铜耗的影响较小，所以槽面积应尽量保持不变，且定子槽槽顶宽度和槽底宽度的比例不改变。表3即为不同槽高度下槽底宽度和槽顶宽度的取值。

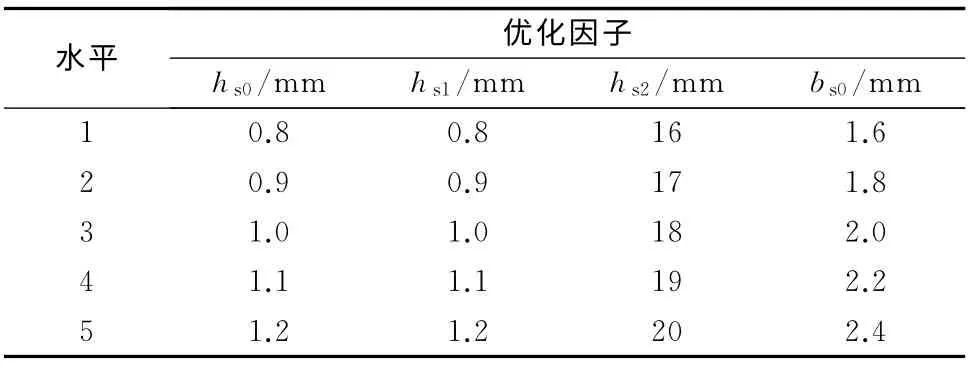
表2 不同优化因子与不同水平正交表

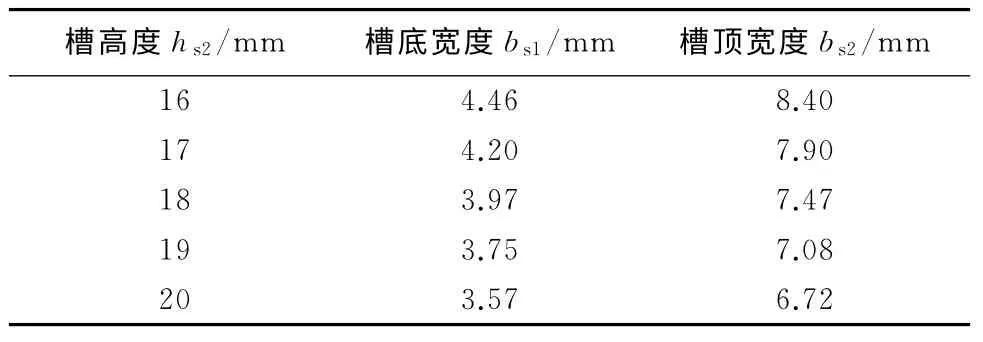
表3 不同槽高度hs2下的槽底宽度和槽顶宽度

选取的优化目标：峰值电流下的转矩脉动Tpp、齿槽转矩Tc、定子铁耗pFe。

2．1 正交实验结果

本文设计的实验因子个数为4，水平数为5，若采用传统的全因子优化方法，即将所有不同水平的组合都做一次有限元仿真并进行比较选出最优设计方案，需要54＝625次有限元仿真。若采用田口法优化设计方法，建立正交实验表，仅需要52＝25次计算，计算时间节约96%［10］。

表4给出了不同因子对应不同水平的正交实验表及有限元仿真结果。其中，T为峰值电流下对应的峰值转矩，Tpp为峰值电流下对应的转矩脉动，Tc为齿槽转矩，pFe为峰值电流下对应的定子铁耗。

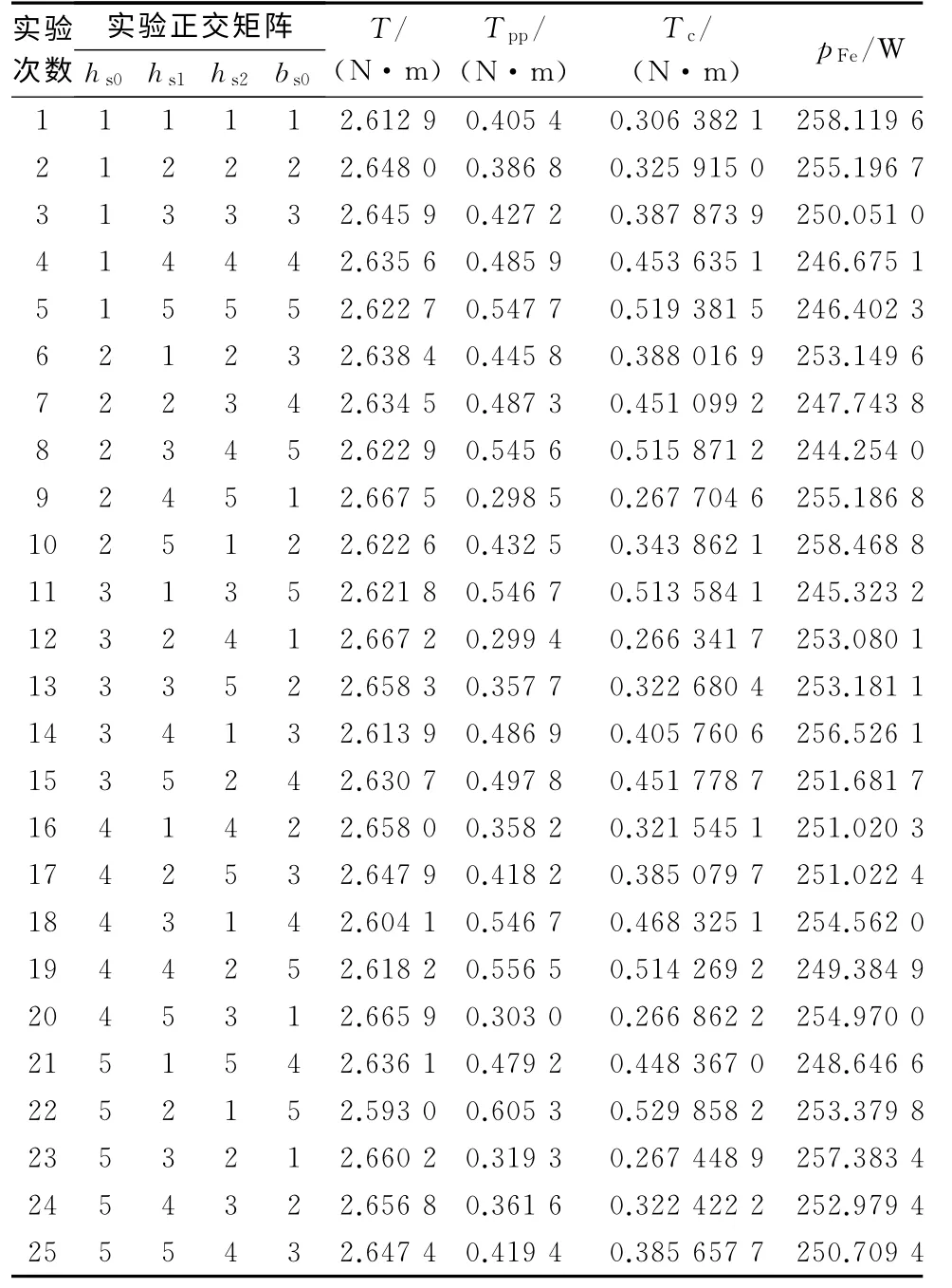
表4 正交实验表及实验结果

2．2 实验结果处理

按照田口法优化的方法，依靠表4的数据，从中获得不同电机性能的平均值，同时获取不同水平的电机性能值，之后获得不同优化目标下对应不同水平的最优组合。

其中计算平均值的公式如下：

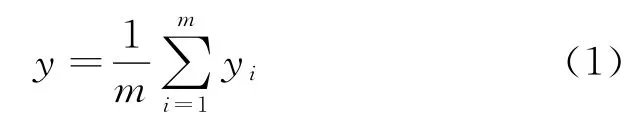
式中：y为因子F的不同电机性能的平均值；m为正交实验总的次数；yi为第i次实验时对应实验结果数值。

表5 各优化目标全体实验平均值

下面利用平均值公式，将不同因子对不同优化目标的影响程度分离出来。其中因子hs2不同水平的定子损耗平均值公式如下：

利用式（2）也可以计算其他不同因子水平下的优化目标值。

从表6 中可以看出：峰值电流下的转矩T与hs0，hs2为正相关关系，与bs0为负相关关系，与hs1为先增大后减小的关系，且在水平4时为最大值；转矩脉动Tpp与bs0为正相关关系，与hs2为负相关关系，与hs0，hs1为先减小后增大的关系，且都在水平4时为最小值；齿槽转矩Tc与bs0为正相关关系，与hs0，hs1为负相关关系，与hs2为先减小后增大的关系，且在水平3时为最小值；定子铁耗pFe与hs0，hs1为正相关关系，与bs0为负相关关系，与hs2为先减小后增大的关系，且在水平4时为最小值。转矩输出均可满足额定输出转矩，因此可以得到转矩脉动Tpp最小、齿槽转矩Tc最小、定子铁耗pFe最小的参数水平组合：hs0（4），hs1（4），hs2（5），bs0（1）；hs0（5），hs1（5），hs2（3），bs0（1）；hs0（1），hs1（1），hs2（4），bs0（5）。通过这些组合可以看到，针对不同的优化目标无法直接统一成一个水平组合，这里我们就需要借助统计学分析手段，选择一个最优的水平组合。

表6 各因子水平下的优化目标值

我们利用方差公式，得到不同因子对电机性能的影响程度，方差计算公式如下：

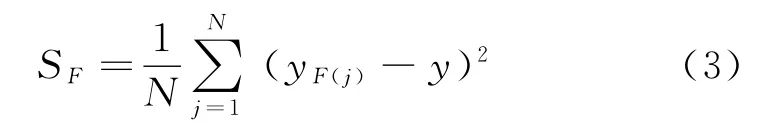
式中：SF为因子F对应不同电机性能的方差；N为实验选取的水平数量；yF（j）为因子F水平j在表6中不同电机性能的实验结果；y为因子F的不同电机性能的平均值。

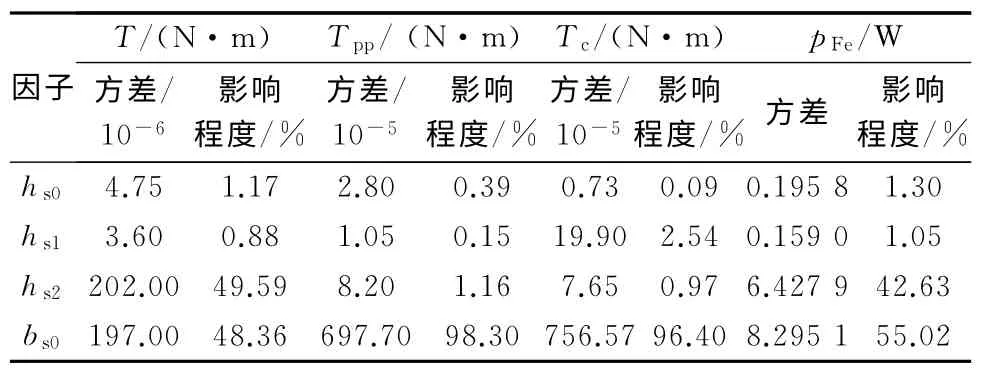
表7 不同因子对电机性能的影响程度

从表7可以得到，不同因子对不同电机性能的作用比例是不同的。根据表7可以得到，bs0对峰值电流下对应的峰值转矩T、转矩脉动Tpp、齿槽转矩Tc、定子铁耗pFe都有较大的影响，hs2对峰值转矩T和定子铁耗pFe影响较大。

2．3 确定优化后的因子水平组合

根据以上分析，在转矩满足电机额定输出扭矩的前提下，hs0，hs1，bs0的选取以降低齿槽转矩为优化目标，hs2的选取以降低定子铁耗为优化目标，最终确定的各因子水平的最优组合：hs0（5），hs1（5），hs2（4），bs0（1）。优化后各因子取值如表8所示。

表8 优化后各因子取值

2．4 优化前后对比

将最终确定的不同因子的最优组合在ANSYS Electronics Desktop软件中实验，表9 为优化后的实验结果，图3为优化前后转矩波形对比图，图4为优化前后定子铁耗波形对比图，图5为优化前后齿槽转矩波形对比图。与优化前的实验结果相比，优化后的实验结果在峰值电流下对应的峰值转矩提高了0．8%，转矩脉动降低了29．57%，齿槽转矩降低了30．69%，定子铁耗降低了1．05%。

表9 优化前后额定电流下的性能对比

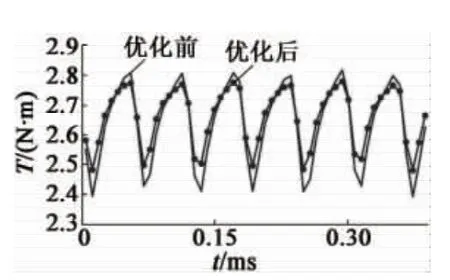
图3 优化前后转矩波形对比图

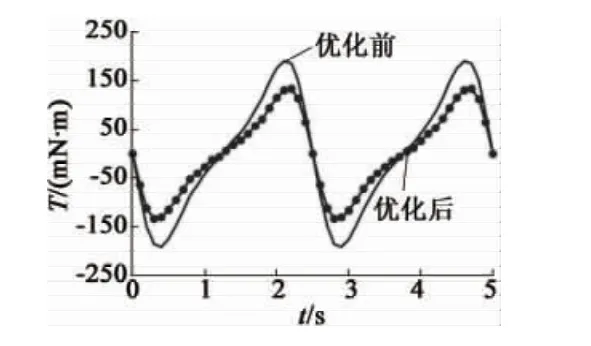
图5 优化前后齿槽转矩波形对比图

3 结 语

本文将田口法应用到永磁同步电机电磁优化设计中。相同额定电流和额定输出转矩时，以降低转矩脉动、齿槽转矩、定子铁耗为优化目标，在定子内外径不变、绕组接线方式不变的约束条件下，得到最优的定子冲片结构。优化后的结构对降低转矩脉动Tpp和齿槽转矩Tc的效果比较显著，对提高相同峰值电流下电机输出转矩T和降低定子铁心损耗pFe具有一定作用，但效果不太明显。

仿真结果表明在永磁同步电机电磁优化设计时，田口法具有方便性和快捷性，对实际电磁优化工作具有积极作用。