基于无人机激光雷达的银杏人工林有效叶面积指数估测*

吴项乾 曹 林 申 鑫 汪贵斌 曹福亮

(南京林业大学 南方现代林业协同创新中心 南京 210037)

人工林是森林生态系统不可或缺的一部分，不仅可为社会经济发展提供优质丰富的木材资源，而且在维持生态系统平衡以及减缓全球变暖等环境保护方面也发挥着重要作用(Brockerhoffetal.， 2008)。我国是世界上人工林面积最大的国家，约69.3万km2，超过世界人工林总面积的1/4(FAO， 2010)。银杏(Ginkgobiloba)在我国种植面积广、时间久，40年及以上银杏株数达28万株，仅果实年产量就达1.6万t(曹福亮， 2007)。近年来，随着银杏人工林种植面积的迅速增长，不仅保障了国家和社会对林木产品的市场需求，而且在森林可持续发展和生态环境重建等方面也具有重要价值。

森林冠层是植物进行蒸腾、呼吸和光合作用等生理过程的主要场所，叶面积指数(leaf area index，LAI)是描述冠层结构及叶片数量和分布情况的有效定量指标(Bequetetal.， 2011； Ryuetal.， 2012； Gonsamoetal.， 2014)，实时、快速、精确估测人工林叶面积指数并掌握其连续空间分布，是实现人工林可持续经营的前提，同时也是人工林生态循环的研究基础(Wulderetal.， 2010； Thomasetal.， 2011)。精确估测银杏叶面积指数并充分掌握其冠层结构特点，是预测银杏人工林地上生物量的重要参考依据(Runningetal.， 1988)，同时也有助于掌握银杏人工林的竞争与生长、评价其立地质量及理解人工林生态系统的功能和生产力(Turneretal.， 2000； 张佳华等， 2002)。

传统以地面实测为主的叶面积指数测量主要通过直接法和仪器测量，可以获得较为精确的叶面积指数； 但地面实测存在效率低、费时费力等问题，且往往只能获得样地尺度的叶面积指数，较难获得林场尺度及更大范围的叶面积指数连续分布信息； 此外，某些直接法(如鲜重打孔法、描形称重法)可能会在一定程度上破坏森林冠层结构(程武学等， 2010)。激光雷达(light detection and ranging，LiDAR)作为一种主动遥感技术，其原理是通过发射激光脉冲到物体表面，然后接收并分析其返回信号，利用LiDAR可以获得高精度的地表及地物的垂直结构信息，如地形和植被等的理论垂直精度可达到15～30 cm(李增元等， 2016)。相较于传统的光学遥感技术，LiDAR数据获取不易受天气及光照条件影响，在获取森林三维结构方面具有独特优势(李德仁等， 2012； 曹林等， 2014； Wulderetal.， 2010； Thomasetal.， 2011)。近年来，随着无人机(unmanned aerial vehicle，UAV)遥感技术的迅速发展，无人机激光雷达在估测林分结构参数方面的研究也逐渐增多(Linetal.， 2011； Wallaceetal.， 2012)。Nagai等(2009)将低频激光扫描仪(SICK LMS-291)和单反相机(Canon EOS 10D)搭载在无人直升机上用于提取冠层数字表面模型(DSM)和纹理特征，制图平均误差为3～10 cm； Jaakkola等(2010)将激光扫描仪(Sick LMS151)、CCD相机(AVT Pike F-421C)、光谱仪(Specim V10H)和热红外相机等搭载在轻巧型多旋翼无人机激光雷达系统上(FGI Sensei)用于估测芬兰针叶林树高，其标准差为13 cm，R2=0.92； Wallace等(2014； 2016)研制出一款低成本激光雷达系统(TerraLuma)，该系统合成了低频扫描仪(Ibeo LUX)和高清录像机，用于澳大利亚东南部桉树(Eucalyptus)单木探测和树木高度估测，单木探测准确率达98%，树木高度估测的R2=0.69～0.84，RMSE=0.92～1.3 m。

目前，基于LiDAR数据估测叶面积指数的方法可归纳为2类。一类是“统计模型法”，即利用LiDAR数据提取的冠层结构特征变量与地面实测LAI构建统计模型，再采用该统计模型进行估测。如Lim等(2003)利用LiDAR点云计算的特征变量与49块地面样地的有效叶面积指数【effective leaf area index，eLAI，即未考虑到叶片的聚集度(clumping index)】实测数据进行回归分析，估测了加拿大北部阔叶林的eLAI； Roberts等(2005)使用LiDAR数据结合多元非线性模型方法，预测了火炬松(Pinustaeda)人工林单木尺度的eLAI(R2=0.61，RMSE=0.23 m2·m-2)。另一类是“孔隙度模型法”，即通过计算激光点云的穿透率，根据比尔-朗博定律(Beer-Lambert law)计算叶面积指数。如Morsdorf等(2006)使用LiDAR数据结合Beer-Lambert定律估测瑞士石松(Lycopodiumjaponicum)的eLAI，通过机载小光斑离散点云数据冠层回波数与地面回波数的比值来遥测eLAI，同时对样地尺度圆形(样地半径2～25 m)进行敏感性测试，结果发现在样地半径为15 m时，LiDAR估测eLAI的效果最佳，其中R2达到0.69，RMSE仅为0.01 m2·m-2； Sasaki等(2008)也利用机载LiDAR数据点云和近红外高光谱数据估测了位于日本大阪府秀塔市温带常绿阔叶林的有效叶面积指数和冠层孔隙度，通过点云的冠层孔隙度计算得到eLAI，结果发现LiDAR估测eLAI的精度(R2=0.76～0.83，RMSE=0.23～0.28 m2·m-2)优于光学数据估测值； Zhao等(2009)对比LiDAR点云数据、光学影像数据以及2种数据融合3种方式来估测eLAI，得出LiDAR估测效果更好，更能满足样地到区域不同尺度eLAI制图的要求。

综观以往研究，大多为单独利用孔隙度模型法或统计模型法估测有效叶面积指数，且多针对欧美北寒带、温带的天然林，而关于人工林方面类似的研究较少。鉴于此，本研究以我国具有典型性和代表性的成片实生银杏林为对象，利用无人机激光雷达获取的高密度LiDAR点云数据，结合45块地面实测样地数据，使用孔隙度模型法和统计模型法对研究区内样地尺度的有效叶面积指数进行估测并验证精度。具体内容包括： 1) 分别使用孔隙度模型法和统计模型法估测eLAI并评价精度； 2) 在通过LiDAR高度特征变量预测eLAI的基础上，逐步引入冠层密度变量、冠层容积比特征和强度特征变量，并评估几组无人机LiDAR高密度点云特征变量对eLAI预测的效果。

1 研究区概况与研究方法

选取江苏省邳州市铁富镇银杏人工林为研究区(34°33′49″—34°34′23″N，118°05′1″—118°06′06″E)，该区气候属半湿润温带季风气候，年降雨量约903 mm，总面积约5 400 hm2(本研究从中选取2 197 hm2银杏人工林)，林下有部分大豆(Glycinemax)等林农复合经营的低矮植被作物。基于八旋翼无人机平台(UAV)获取的高密度激光雷达点云数据和样地实测有效叶面积指数(eLAI)，结合孔隙度模型法、统计模型法估测样地尺度eLAI。步骤如下： 首先，对LiDAR原始点云数据进行去噪、分类处理，通过插值方法得到数字高程模型(digital elevation model，DEM)，利用DEM进行高度归一化以获得归一化点云LiDAR数据； 然后，将样地实测eLAI与提取的多组LiDAR特征变量结合多元逐步回归方法构建eLAI估测模型(统计模型法)，同时，根据比尔-朗博定律(Beer-Lambert law)结合LiDAR点云提取的孔隙度(P)估测eLAI(孔隙度模型法)； 最后，利用样地实测有效叶面积指数对模型的精度和实用性进行评价。研究技术路线如图1所示。

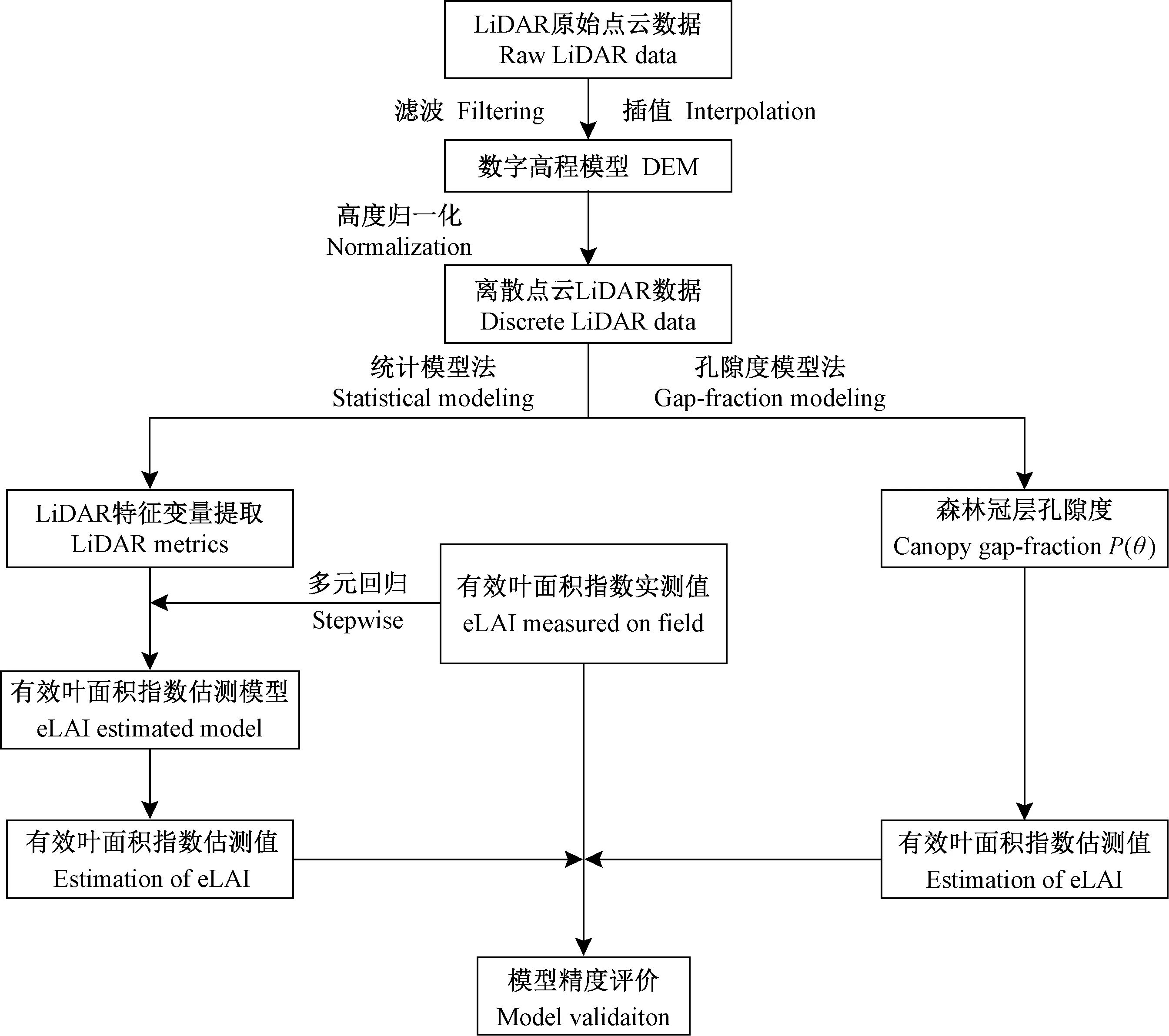
图1 研究技术路线Fig.1 Technological route of this research

1.1 样地选取

基于森林资源二类调查数据、林场种植历史记录数据和高分辨率影像数据，在研究区银杏核心分布范围选取5块1 km×1 km的正方形无人机采样区，按照典型选样方法在5块样地内布设圆形小样地各9块(半径为15 m)，样地中心坐标由Trimble GeoXH6000 Handhelds手持GPS获取，并通过JSCROS广域差分系统进行位置校正以获取亚米级精度的坐标信息。研究区及样地分布如图2所示。

1.2 地面数据采集

地面调查时间为2016年10月，在研究区设置45块圆形样地(半径为15 m)。样地调查过程中，对胸径超过5 cm的单木逐一测定其胸径、树高、枝下高和冠幅，并将测量所得单木信息统计得到样地尺度林分统计特征，即平均胸径(cm)、Lorey’s平均树高(m)、样地株数、样地密度(hm-2)和有效叶面积指数(m2·hm-2)。根据提取的激光雷达Cover特征量(即首次回波中高于1 m的激光返回点占所有返回点的比例)大小将样地划分为3组(第1组Cover： 0.08～0.20； 第2组Cover： 0.21～0.31； 第3组Cover： 0.32～0.83)。通过对比h95(森林冠层首次回波高度垂直分布的95分位数)、hcv(归一化点云高度的变异系数)和Cover这3个激光雷达特征变量的分组效果发现，Cover分组对叶面积指数的估测精度最高，可以用来评价样地的树冠覆盖度以表示样地内单木生长程度。比较分组估测模型与总体估测模型的精度发现，总体模型估测精度高于分组模型。研究区样地分组及参数汇总如表1所示。

图2 研究区正射影像及样地空间分布Fig.2 The orthophoto of study area and the spatial distribution of the plots

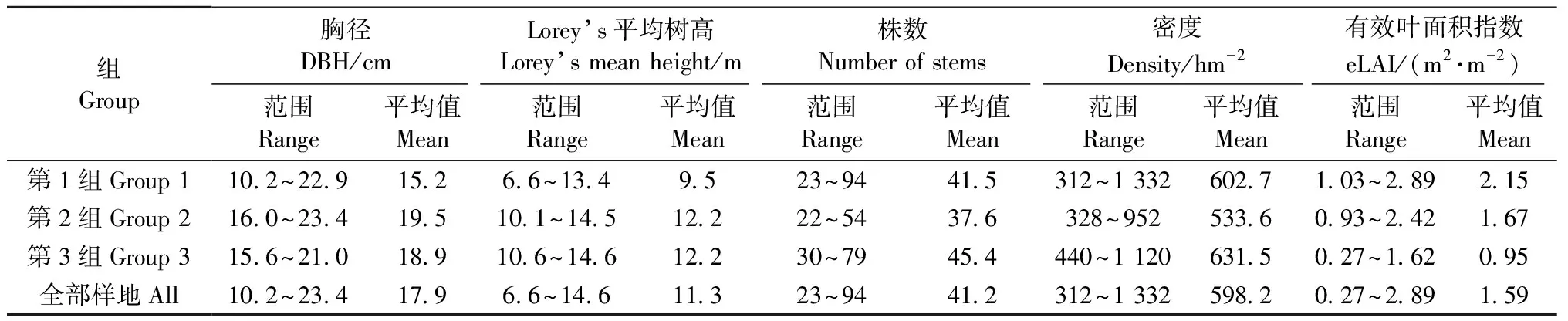
表1 研究区样地林分参数调查信息汇总Tab.1 The summary of plot-level stand characteristics

有效叶面积指数(eLAI)通过LAI-2200测量获得，考虑天顶角A的最外圈数据可能存在地物遮挡以及蓝光多次散射效应的影响，使用1～4内圈数据计算有效叶面积指数。具体操作方法如下： 在样地内选取2条平行的长度30 m测线(方向垂直于太阳光照)，2条测线中点分别距样地中心7.5 m。将LAI-2200置于距离地面1 m高的位置进行测量，以防止低矮植被的影响。测量前在空旷的林窗下匹配2支探杆的时间和测量参数，并保证视角盖均为90°且方向一致； 匹配后，其中一支探测杆置于林窗下每隔10 s自动采样1次(A)，另一支在样地内沿着测线每隔4 m采样1次(B)； 测量结束后，A和B通过时间匹配，联合计算eLAI。每个样区内16个测点的eLAI平均值作为该样区的eLAI。有效叶面积指数地面实测方法如图3所示。

1.3 LiDAR点云获取及预处理

LiDAR数据由八旋翼无人机平台搭载的Velodyne激光扫描仪(VLP-16)于2016年10月13—17日获取。无人机平台飞行高度60 m，飞行速度4.8 m·s-1，条带之间间隔50 m，LiDAR扫描仪激光波长903 nm，扫描角设定±30°，发散度3 mrad，地面光斑直径18 cm，脉冲发射频率21.7 kHz，扫描频率16 s-1，最终获取的LiDAR点云平均点密度约159 pts·m-2。对于获取的原始数据， 首先根据阈值法对噪声点进行识别并删除，同时对点云地面点进行识别分类； 然后通利用反距离加权法(inverse distance weighted，IDW)结合分类的地面点插值以生成DEM； 最后利用DEM对点云进行高度(z)归一化以获得高度归一化点云数据。

1.4 LiDAR特征变量提取

使用DEM将离散点云归一化后，计算样地尺度的激光雷达特征变量。本研究共计算6类(4组)特征变量，特征变量及描述如表2所示。

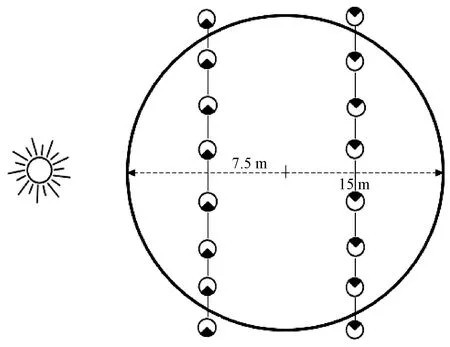
图3 有效叶面积指数地面实测方法示意Fig.3 The sketch of eLAI measured on ground

表2 LiDAR特征变量及其描述Tab.2 The description of LiDAR metrics

枝叶剖面(foliage profile，FP)是树木枝叶在垂直空间结构上的分布状况，描述了冠层内叶面积指数随着高度增长的变化情况(Lovelletal.， 2003)，FP值为树木冠层指定高度上单位体积内的枝叶面积之和(Riaoetal.， 2003)。FP与LAI 在垂直高度上的分布密切相关(Radtkeetal.， 2011)，其表达式为：

(1)

式中：L(z)为在高度z处的累积有效叶面积指数；z1、z2为冠层高度。

采用Weibull函数拟合FP，本研究Weibull参数不是根据胸径算出的表示样地径阶的参数(模型因变量)，而是利用LiDAR垂直枝叶剖面的Weibull拟合计算的特征变量(模型自变量)，公式如下：

(2)

式中：Hmax为最大树高；α为尺度参数；β为形状参数(Coopsetal.， 2007)。

Weibull函数中，α和β通常通过最大似然估计法(maximum likelihood estimation，MLE)解算求得。先前研究表明，MLE在预测森林Weibull分布函数时拟合效果较好(Gorgosoetal.， 2007)，其计算公式如下：

(3)

(4)

式中：n为样本个数；xi为每株单木的冠层容积。

1.5 孔隙度模型法估测有效叶面积指数

根据光传输特性，当光通过某种介质后，能量会有所减弱。如果将森林冠层当成一种均匀介质，那么影响光穿透后衰减的重要原因是冠层“孔隙度”，可通过Beer-Lambert定律算出。该定律假设光进入冠层前的初始入射能量为I0，通过距离为m的均匀介质后，衰减后的能量为I，公式如下：

I=I0exp(-m)。

(5)

植物冠层消光系数直接决定其对辐射的截获量，因为穿过的介质为均匀介质。若设消光系数为a，介质浓度为C，那么有：

(6)

将式(4)、(5)合并，得：

I=I0exp(-aCm)；

(7)

(8)

式中：I0/I表示光的穿透率，设为P。

消光系数G(θ)是与叶倾角密切相关的系数，P可以用下式表示：

P(θ)=e-G(θ)L/cosθ。

(9)

根据激光雷达计算叶面积指数：

(10)

式中：θ为激光雷达扫描角。

本研究区内为银杏纯林样地，利用19块单木定位样地(使用Postex林木定位仪确定每株银杏单木位置)，通过最近邻体分析法(nearest neighbor analysis，NNA)计算研究区内树木水平分布情况，结果表明银杏单木在水平方向上均呈随机分布(胡艳波等， 2014； 赵中华等， 2016)。因银杏为喜光阔叶树种，为了最大化提高光能利用率进行光合作用，冠层中的叶片会向各方向生长，整体叶倾角在空间上近似为球形分布。假设激光垂直入射冠层，因此可将消光系数设为0.5(Weissetal.， 2004； Morsdorfetal.， 2006)。P(θ)可通过下式算出：

(11)

式中：n为LiDAR发射的总光点数；nground为LiDAR穿透森林冠层后到达地面的光点数。

基于以上公式，可通过孔隙度模型法算出有效叶面积指数，使用地面实测有效叶面积指数对孔隙度模型法估测的有效叶面积指数进行精度评价。

1.6 统计模型法估测有效叶面积指数

通过逐步回归法构建的线性方程预测有效叶面积指数，模型形式如下：

y=c0+c1q1+c2q2+…+cnqn+ε。

(12)

式中：y为因变量；q为自变量；c为常数；ε为误差。

本研究中，地面实测有效叶面积指数为因变量，LiDAR提取的多个特征变量组为自变量，将自变量逐个引入模型，每引入1个自变量都进行F检验(P<0.05)，当原先引入的自变量由于后面自变量的引入变得不再显著时，则将其删除，直到将所有自变量筛选完为止，最终筛选出与有效叶面积指数相关性最高的3个自变量(自变量的数量并未增加)进行建模(Nssetetal.， 2008； Breidenbachetal.， 2010)。采用决定系数(R2)评价模型拟合效果，采用均方根误差(RMSE)、相对均方根误差(rRMSE)和赤池信息量准则(AIC)评价回归模型精度(Akaike，1974； Getisetal.， 2004)。计算公式如下：

(13)

(14)

(15)

AIC=-lgL+2k。

(16)

在模型参数已确定的情况下，对45块地面实测样地全部进行交叉验证(cross-validation)，首先随机选取任意1块样地的eLAI作为验证数据，将其余44块样地的eLAI进行建模，然后利用拟合的模型与随机选取1块样地的eLAI进行检验，如此重复进行直到所有样地全部验证完毕。

2 结果与分析

表3为选取不同LiDAR特征变量组合参与建模估测eLAI的模型形式及精度评价。由表可见，仅使用高度特征变量建模预测eLAI时精度最低(R2=0.44，rRMSE=48.3%，AIC=202.5)，逐步引入其他特征变量后，预测精度明显提升。使用所有LiDAR特征变量建立模型估测eLAI时精度最高(R2=0.78，rRMSE=22.1%，AIC=158.3)，高于使用高度和密度变量建立模型估测eLAI的精度(R2=0.67，rRMSE=43.2%，AIC=172.1)，再其次是使用高度和冠层容积变量建立模型变量预测eLAI的精度(R2=0.65，rRMSE=43.8%，AIC=175.2)。

表4为不同Cover分组的有效叶面积指数估测模型比较及交叉验证精度评价。由表可见，通过Cover将45块样地分为3组后，每组模型交叉验证精度相比于总体样地模型都有所提升。

表3 不同特征变量组合作为预测变量的有效叶面积指数估测模型比较及精度评价Tab.3 eLAI model by different metrics and their accuracy assessments

表4 不同Cover分组的有效叶面积指数估测模型比较及交叉验证精度评价Tab.4 eLAI models by different Cover and cross-validation results

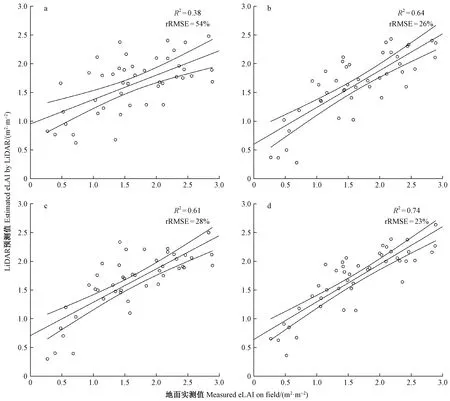
图4 地面实测eLAI与统计模型法预测eLAI交叉验证结果Fig.4 The cross-validation results of the filed-measured and statistical model predicted eLAIa为基于高度特征变量建模； b为基于高度+密度特征变量建模； c为基于高度+冠层容积特征变量建模； d为基于所有提取的特征变量(含强度特征变量)建模。a is modelled by height percentile； b is modelled by height percentile and density metrics； c is modelled by height percentile and canopy volume metrics； d is modelled by all metrics(contain intensity metrics).

统计模型法预测有效叶面积指数模型交叉验证结果如图4所示。仅通过LiDAR高度特征变量参与建模的精度最低，R2为0.38(rRMSE=54%)(图4a)； 使用高度和密度特征变量组合参与建模的精度为R2=0.64(rRMSE=26%)(图4b)； 通过高度和冠层容积特征变量组合与地面实测eLAI建立模型的精度为R2=0.61(rRMSE=28%)(图4c)； 当使用所有LiDAR特征变量(包括强度特征变量)建模时精度最高R2为0.74(rRMSE=23%)(图4d)。加入其他类型特征变量后，比仅通过高度特征变量建立模型的预测效果都有不同程度提高，其中，基于所有提取的特征变量建模预测效果最佳，通过高度和密度特征变量组合估测eLAI效果次之，最后是通过高度和冠层容积特征变量组合估测eLAI的精度。

根据Cover分组后，不同组统计模型法预测有效叶面积指数估测模型交叉验证结果如图5所示。分组后模型估测精度皆优于不分组估测精度(R2=0.74，rRMSE=23.0%)(图5d)； 在分组估测模型中，第2组估测有效叶面积指数精度最高(R2=0.88，rRMSE=12.6%)(图5b)，其次是第1组(R2=0.86，rRMSE=15.6%)(图5a)，第3组估测有效叶面积指数精度最低(R2=0.79，rRMSE=21.9%)(图5c)。

孔隙度模型法预测eLAI精度如图6所示。相较于4种点云特征变量统计模型法估测精度，孔隙度模型法估测精度(R2=0.71，rRMSE=32.0%)高于仅通过高度百分数建模估测、高度和密度特征变量组合建模估测以及高度和冠层容积特征变量组合估测eLAI的精度，但比通过所有特征变量(包括强度特征变量)建模预测精度低。

根据激光雷达算出的银杏人工林Cover特征量，将45块样地分为3组，选取3组中具有典型代表性样地如图7所示。对比3组样地正射影像，第1组样地密度最高，第2组样地密度最低，第3组样地密度较第2组有所增高(a1—c1)； 对比3组样地球面镜影像，第1组样地天空所占比例最大，第2组样地次之，第3组样地天空所占比例最小(a2—c2)； 观察3组样地激光雷达点云及点云剖面图，第1组样地平均树高最低(约8.14 m)但激光雷达点密度最高，第2组样地平均树高比第1组样地更高(约11.52 m)但激光雷达点密度降低，第3组样地平均树高最高(约12.76 m)但激光雷达点密度比第2组高(a3—c3，a4—c4)。

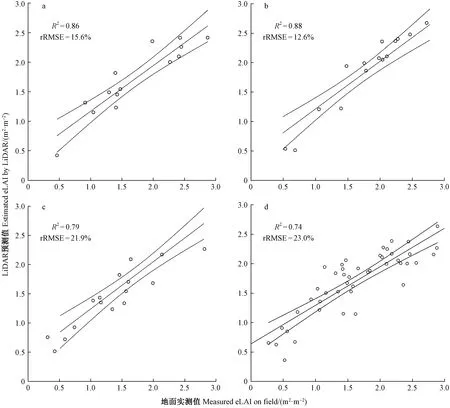
图5 不同Cover组地面实测eLAI与统计模型法预测eLAI交叉验证结果Fig.5 The cross-validation results of the filed-measured and statistical model predicted eLAI indifferent Covera为第1组结果； b为第2组结果； c为第3组结果； d为所有样地结果。a is the result of Group 1； b is the result of Group 2； c is the result of Group 3； d is the result of all plots.

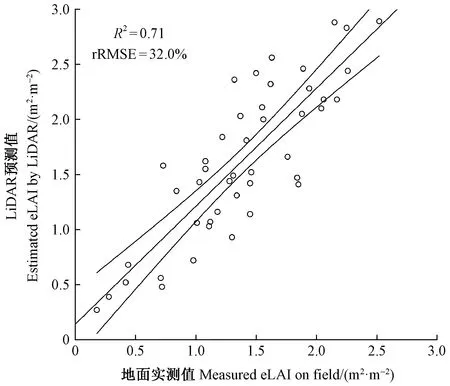
图6 孔隙度模型法估测eLAI与地面实测eLAI拟合精度Fig.6 eLAI estimated by gap-fraction model

3组样地冠层垂直结构分布剖面【计算方法详见Coops等(2007)】如图8所示。由3组典型样地冠层高度分布(canopy height distribution，CHD)可知，第1组样地激光雷达点密度最高处在3～5 m之间，第2组样地激光雷达点密度最高处在7.2～10.5 m之间，第3组样地激光雷达点密度最高处在3～11 m之间，3组样地平均树高依次增高，冠幅增大(a1—c1)； 由3组样地枝叶剖面(FP)随冠层高度变化情况可知，第1组样地枝叶剖面峰值最大在约3.5 m树高处，第2组样地枝叶剖面峰值最大在约8.5 m树高处，第3组样地枝叶剖面峰值最大在约9.0 m树高处，3组样地最大峰值在冠层中的高度分布依次增高，表明冠幅最大的枝叶的高度变高(a2—c2)，且CHD和FP分别与Weibull函数曲线拟合形式较好； 由3组样地的有效叶面积指数累积曲线可知，最高处的eLAI为该样地的eLAI，第1组样地eLAI为0.48 m2·m-2，第2组样地eLAI为1.8 m2·m-2，第3组样地eLAI为2.3 m2·m-2。

3 讨论

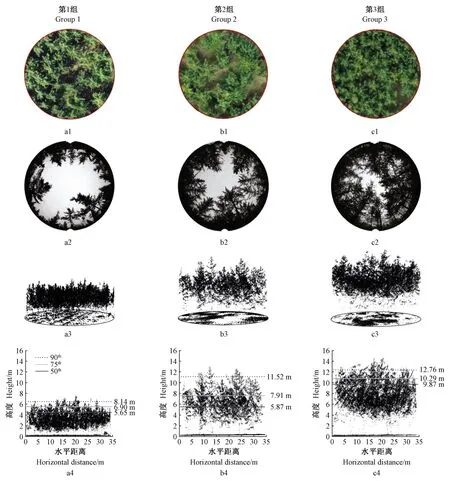
图7 3组典型样地正射影像(a1—c1)、球面镜影像(a2—c2)、激光雷达点云(a3—c3)及激光雷达点云剖面(含50、75、95高度分位数位置)(a4—c4)Fig.7 The orthophotos(a1—c1), spherical HemiVeiw photos(a2—c2), point clouds (a3—c3)and profile(contain 50th, 75th, 95th height percentiles)(a4—c4)of three typical plots

本研究基于无人机激光雷达数据并结合45块地面银杏人工林样地实测数据进行eLAI估测，结果发现，使用统计模型法构建eLAI估测模型时，引入多种变量(密度、冠层容积和强度特征变量)后，估测精度高于仅使用高度特征变量建立模型的精度。Nsset(2002)利用机载激光雷达反演挪威不同林龄森林结构参数，通过提取激光雷达点云冠层高度和冠层密度变量，得出高度和密度变量组合的估测精度优于仅通过高度或密度变量估测精度； Cao等(2016)通过激光雷达估测亚热带森林地面生物量时，利用激光雷达点云特征变量和强度相关信息联合建模精度高于仅通过点云特征变量建模的精度； Morsdorf等(2006)通过建立离散小光斑激光雷达不同尺度(圆形半径2～25 m)的冠层回波数和地面回波数的比值与基于半球影像估测的LAI进行回归分析，建立LAI估测经验方程，发现光斑半径为15 m时效果最好，决定系数为0.69，其孔隙度模型法估测eLAI精度与本研究相近； Peduzzi等(2012)利用多回波LiDAR数据计算样地尺度的LAI以及不同高度处的覆盖度等变量与LAI地面实测值进行回归分析，并用于卡罗莱纳州和弗尼吉亚州北部松树林LAI估测，决定系数最高达0.77，RMSE为0.42，与本研究统计模型法估测eLAI精度相近。利用统计模型法估测eLAI时，引入多种特征变量后的估测精度高于仅通过高度特征变量估测精度，这是因为在引入其他点云特征变量后，新的特征变量组合对冠层结构刻画更为全面，从而提升了有效叶面积指数估测精度。本研究选取强度特征变量估测有效叶面积指数，取得了较高精度(R2=0.74，rRMSE=23%)，与前人研究结果相似。Mariano等(2010)利用机载LiDAR的高度和强度特征变量估测地中海地区的森林生物量，结果发现使用高度和强度变量组合建模的精度明显优于仅通过高度特征变量建模的精度，同时，预测模型也选取了较高的强度特征变量作为预测因子(I95)。本研究中由于无人机飞行高度恒定，且研究区处于平原地区； 同时，样地大多处于无人机激光雷达扫描的下方，避免了能量因为传输距离增大(扫描角增大)的损耗，因此使得未校正的强度变量适用于本研究有效叶面积指数的估算(Kiddetal.， 2016； Brunaetal.， 2019)。

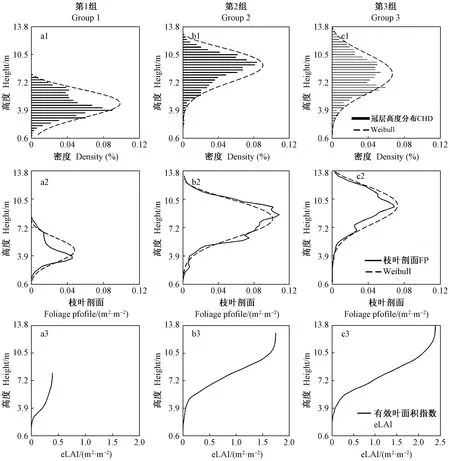
图8 3个典型样地冠层高度分布(CHD)(a1—c1)、枝叶剖面(FP)(a2—c2)与Weibull拟合曲线及有效叶面积指数(eLAI)累积曲线(a3—c3)Fig.8 Canopy height distribution(a1—c1)and foliage profile(a2—c2)fitted with Weibull function, and eLAI accumulate(a3—c3)

对比图7中的 3个组别，第1组树高较低，但种植密度较大，激光雷达点云多集中在冠层中上部，结合银杏人工林的生长情况，第1组为幼龄林； 相对于第1组，第2组密度有所降低，但是树木高度增大，此组类型为随着树木生长发育进行一系列抚育间伐，林分覆盖度有所增加，因此激光雷达点云也多集中在冠层中上部，穿透到地面的点云数量较少； 第3组中，树高较前2组有所增大，密度与第2组相比较为相近，但覆盖度增加，根据银杏生长规律，银杏属于强喜光树种，随着树龄增加，对光照的要求也愈加迫切(曹福亮， 2007)，其中上部冠层会因为趋光性而逐渐向有阳光照射区域生长，冠幅变大，只有极少部分激光雷达点云可以穿透树冠到达地面，此组银杏为成熟林，相较于前2个生长阶段，激光雷达点云分布更偏于上层。综合3个生长阶段激光点云分布情况，与模型选取的75%、95%高度分位数来估测eLAI的情况一致。

从冠层枝叶以及非光合作用组织在垂直高度上的点云分布情况(图8)可知，3组样地树木依次增加，所对应的生长时期也不同。第1组样地内平均树高较低，栽植密度大，中下部点云密度较多，由于是幼龄林，银杏的粗壮枝叶集中在中层。第2组样地内平均树高较第1组增加，密度降低，随着银杏生长，进行抚育间伐，主枝变大并朝上生长，因此冠层中上部点云分布较多。第3组样地平均树高比第2组样地增加，但冠层中高密度点云向下偏移，冠层中部点云密度最大，这是由于银杏林逐渐成长为成熟林，主枝不再随着树高增长而升高，因银杏趋光性而向有光照区域生长，主枝变粗大，冠层中部枝叶覆盖度增加，所以在树高6～10 m范围内，激光雷达点云数分布较多。图8b1—b3为枝叶剖面(FP)，描述了在垂直高度上冠层枝叶面积的分布情况(Juppetal.， 2009)。随着树龄增长，银杏林分不断成熟，其枝叶剖面分布更加均匀且峰值向上偏移； CHD和FP与Weibull函数拟合较好(图8a1—a3、b1—b3)，基本可以得到分布的形状和范围。图8c1—c3反映了有效叶面积指数随高度的变化情况，3组样地中，冠层中部eLAI增长速度较快，底部和顶部增长速度较慢，这是由于银杏中部冠层生长较为茂盛，集中了较多的粗大枝。本研究利用无人机激光雷达数据对研究区内样地尺度的有效叶面积指数进行估测和方法比较及精度验证，未能进行尺度变换实现整个无人机数据获取区域(包含5个“无人机采样区”)的叶面积指数估测，在今后的研究中，可以尝试进行有效叶面积指数空间分布外推，实现整个研究区的有效叶面积指数空间分布估测。

4 结论

本研究利用多旋翼无人机激光雷达系统获取的点云数据，结合45块地面实测样地数据，使用孔隙度模型法(通过计算点云的冠层穿透率，根据Beer-Lambert 定律计算有效叶面积指数)和统计模型法(首先通过地面实测的有效叶面积指数和所提取的LiDAR特征变量建模，然后借助拟合的模型估测有效叶面积指数)对我国典型平原银杏人工林进行样地尺度的有效叶面积指数估测。结果表明： 统计模型法估测有效叶面积指数时，仅通过高度特征变量估测精度为R2=0.38(rRMSE=54%)，分别引入多种特征变量，即冠层密度变量、冠层容积比特征和强度特征后，估测叶面积指数精度有所提高，精度分别为R2=0.64(rRMSE=26%)、R2=0.61(rRMSE=28%)、R2=0.74(rRMSE=23%)； 利用Cover分组后建模结果表明，分组建模的精度优于不分组建模的精度； 孔隙度模型法估测有效叶面积指数的精度为R2=0.71(rRMSE=32.0%)。