基于FPGA的图像畸变矫正算法研究

毛昕蓉，刘铠铭，汪乐意，韩晓冰

（西安科技大学 通信与信息工程学院，陕西 西安 710054）

引言

当具有理想形状的透镜与图像传感器保持严格平行时，摄像头采集的图像不存在任何非线性畸变。但由于制造工艺、安装误差等原因，现实中不存在理想的透镜，而且将透镜和图像传感器平面保持严格平行是非常困难的[1]。因此，摄像头真实的成像效果往往会存在一定程度的非线性畸变[2]。含有非线性畸变的图像在一些定量分析，图像测量领域中会降低图像中物体的几何位置精度[3]，所以，在进行相关图像处理之前，需要完成畸变矫正这一预处理。基于传统的串行处理器实现图像畸变矫正的实时性会随着图像分辨率的提升而变差，不适合应用在实时性要求高的场景。相比之下，融合了ASIC 和基于处理器系统的最大优势的FPGA，既能提供硬件定时的速度与稳定性，其灵活性也与基于处理器系统上运行的软件相当[4]，非常适合实现图像的实时畸变矫正。因此，本文针对FPGA 实现图像畸变矫正算法做了相关的理论研究。

1 畸变矫正算法

基于图像映射的畸变矫正算法由两个基本操作组成：一是对图像平面上的像素点按照畸变模型进行重新排列；二是对空间变换后的像素点的灰度值重新赋值[5]。根据处理数据流向的不同，重新排列的方式可分为两种[6]：一是计算源图像任意像素点经映射后在目标图像中的坐标位置，即前向映射；二是计算目标图像任意像素点经映射后在源图像中的坐标位置，即逆向映射。前向映射和逆向映射的关系如(1)式所示：

式中：(u,v)是目标图像像素坐标；(x,y)是源图像像素坐标。相比前向映射，遍历目标图像的像素点的逆向映射不会出现空点像素问题，因此像素点的重新排列方式常选用逆向映射。逆向映射坐标的获取可利用相机的内参数矩阵H、畸变系数ki(i=1,2,3)和pi(i=1,2)来计算。假设(xp,yp)是目标图像上的像素点，(xs,ys)为像素点(xp,yp)对应的逆向映射坐标，则逆向映射坐标(xs,ys)计算如(2)式和(3)式所示[7]：

由于经逆向映射得到的坐标一般是非整数，即计算出的像素坐标不落在原图像的像素点上而是在其附近，故需要进行插值处理。考虑到不同插值算法的插值效果和硬件实现成本[8]，本文利用双线性内插值对空间变换后像素点的灰度值重新赋值，如图1 所示。

双线性内插值计算过程如(4)式所示，在两个方向分别进行一次线性插值后，可得到目标像素的灰度值I[9]。

2 基于FPGA 的图像畸变矫正算法优化

2.1 基于逆向映射表的图像畸变矫正

从(2)式和(3)式中可以看出，逆向映射坐标(xs,ys)的计算需要经过非常复杂的运算，主要包括多阶矩阵求逆，矩阵与坐标相乘，各种参数（浮点数）与坐标相乘等运算。若是直接利用FPGA 在线计算逆向映射坐标，将会耗费大量的乘法器等资源[10]，而FPGA 芯片上如乘法器之类的资源是有限的，FPGA 芯片越低端，数量越少，因此乘法器等资源需要节约使用。而且FPGA 本身也并不适合实现太复杂的运算，因此利用FPGA 进行在线计算逆向映射坐标是不可取的。

由于相机的内参数矩阵、畸变系数是固定不变的[11]，即目标图像到源图像的坐标映射是固定不变的，因此可先将目标图像的像素点遍历一遍，计算出各像素点的逆向映射坐标(xs,ys)，形成一个逆向映射表，然后将逆向映射表存入FPGA 的片上ROM 中。在进行逆向映射时，只需通过查找片上ROM 中的逆向映射表就可以获得较高精度的逆向映射坐标，这比计算一个参数模型快得多，避免了在FPGA 上耗费大量的逻辑资源去实现复杂的在线计算。该过程如图2 所示。

得到逆向映射坐标后，FPGA 还需实现目标像素点的重新赋值。此时可凭逆向映射坐标从帧缓存中获得对应的插值窗口的4 个角点的灰度值进行双线性内插值计算，并将计算得到的灰度值赋给目标图像的像素点即可。由(4)式可知，双线性内插值计算主要是小数与整数的乘法运算和加法运算[12]，因此FPGA 可以较小的逻辑资源直接实现双线性内插值计算。

图1 双线性插值Fig.1 Bilinear interpolation

图2 基于逆向映射表的逆向映射Fig.2 Reverse mapping based on reverse mapping table

综上所述，利用FPGA 实现矫正图像畸变算法的过程如图3 所示。

图3 矫正图像畸变算法的FPGA 实现Fig.3 Implementation of image distortion correction algorithms based on FPGA

图3 中，图像畸变矫正算法的FPGA 实现过程为：

步骤1：从逆向映射表（存储于片上ROM）中查找出与目标图像（经矫正的图像）当前像素点对应的逆向映射坐标 (xs,ys)；

步骤2：凭逆向映射坐标(xs,ys)从帧缓存中获取对应的插值窗口的4 个角点的灰度值并进行双线性内插值计算，将计算得到的灰度值赋给当前像素点；

步骤3：跳到目标图像的下一个像素点，重复步骤1 和步骤2，直到遍历完一帧图像中的所有像素点。

2.2 逆向映射表的存储优化

常见的FPGA 芯片的片上内存容量普遍较小，如型号为Cyclone IV EP4CE115F29 的FPGA 芯片有432 个M9K 内存模块，总大小约为3.79 Mb。而需要进行畸变矫正图像尺寸越大，则对片上内存的容量需求越大。以分辨率为640×480 像素的图像为例，其逆向映射坐标(xs,ys)中的xs（表示列）可由10 位整数位，7 位小数位的二进制表示；ys（表示行）由9 位整数位，7 位小数位的二进制表示，此时逆向映射表的大小如(5)式所示：

由(5)式可知，片上ROM 无法存储未经压缩的逆向映射表，针对这个问题，Akin 提出了将逆向映射表存进DRAM 中，而郑永瑞则将其固化在ROM 芯片中，开始矫正时缓存到DDR2 芯片中[13]。但这些方法会增加设计的复杂度并降低处理速度，为了发挥片上ROM 的硬件加速功能，需将逆向映射表压缩至合适的大小。映射坐标 (xs,ys)的获取方式如图4 所示。

图4 逆向映射坐标(xs,ys)的获取Fig.4 Acquisition of inverse mapping coordinates (xs,ys)

由于摄像头采集的图像因非线性畸变造成的变形存在着连续性，即目标图像中毗邻像素点的逆向映射坐标是平滑的且变化缓慢，因此可仿效图像缩放的原理[14]，对逆向映射表进行压缩。从计算的角度来看，最简单的压缩方式就是对逆向映射表进行降采样[15]，从而降低逆向映射表的分辨率，使其能够存进片上ROM，然后在FPGA 上通过插值来重建期望的逆向映射表。此时，图3 中逆向

1）基于降采样压缩逆向映射表

以分辨率为640×480 像素的图像为例，未经压缩的逆向映射表分辨率为640×480 像素。图5 所示为逆向映射表的一部分（n+1 行641 列，第641列为重建需要增加的一列）。

图5 中，k=640/n，增加的第641 列是为了保证第k个窗口在重建时有一个完整的插值窗口，第641 列复制了第640 列的数值（同理增加第481 行）。对逆向映射表进行降采样时，可在水平和垂直方向上每隔n-1 个存储单元采样一个存储单元存入新的逆向映射表，此时经过压缩的逆向映射表分辨率rcomp如(6)式所示，经压缩的逆向映射表分辨率rcomp与未压缩的逆向映射表分辨率rori的比例因子S如(7)式所示。

图5 逆向映射表的压缩Fig.5 Compression of reverse mapping table

从(7)式可以看出，当n越大，比例因子S越大，则压缩程度越大，逆向映射表对存储空间的需求越低。

2）基于插值法重建逆向映射表

不同的插值算法重建降采样后的逆向映射表，所需的采样点数量，消耗的逻辑资源也不同。3 次内插法所需的采样点数量较少，但算法复杂度高，在计算给定位置的映射时所需的逻辑资源较多，计算速度慢；双线性内插法所需的采样点数量虽然要多于3 次内插法，但由于双线性内插法较简单，在计算给定位置的映射时所需的逻辑资源较少，计算速度快。因此，本文采用双线性内插法来重建期望的逆向映射表，其原理如图6 所示。

由于逆向映射表中的一个存储单元同时存储了xs和ys，故xs和ys的值需分别计算。以计算xs为例，图6 中黑色的点I1、I2、I3和I4为降采样后的逆向映射表中的4 个xs，灰色点I和空心点都为重建逆向映射表时数值未知的xs。设点I1、I2、I3和I4之间的水平和垂直距离都为n，Δx为点I的水平方向权值，Δy为点I的垂直方向权值，利用双线性内插法去拟合4 个点I1、I2、I3和I4之间的(n+1)2-4 个xs的数值，以图中的点I为例，其计算过程如(8)式所示：

从(8)式可以看出，当在FPGA 上利用双线性内插法在线重建逆向映射表时，需要实现除数为n的除法运算。在FPGA 上实现除数不等于2i(i=1,2,3···)的除法会耗费较多的逻辑资源，但如果除数为 2i(i=1,2,3···)时，硬件实现上只需要做右移i位的操作便可实现除法，因此当n等于2i(i=1,2,3···)时，硬件实现双线性内插法计算的成本最小。而经降采样后逆向映射表的大小为原来的1/S。

3）优化后算法的分析

基于坐标映射的图像畸变矫正算法是目前最为成熟和有效的畸变矫正方法。但基于不同插值方法的映射算法在图像质量，资源消耗等方面都存在一定差[16]，这些差异会影响最终在FPGA 上实现的效果。常用的插值方法有最邻近元法和3 次内插值方法。最邻近元法虽然速度快，资源使用量小，但是矫正后的图像质量不佳，易产生锯齿失真。3 次内插值法能够得到较好的图像质量，但是算法代价过大，会消耗大量的加法器和乘法器资源，十分不适于在FPGA上进行实现。本文所采用的双线性内插方法结合了两者的优点，在保证图像质量的同时，有效降低了算法开销和逻辑资源占用，使之能更好地在FPGA 平台上进行实现。表1 给出了基于几种不同插值算法的畸变矫正算法的比较。

表1 3 种畸变矫正算法的比较Table 1 Comparison of three distortion correction algorithms

图6 双线性内插法实现逆向映射表的重建Fig.6 Reconstruction of reverse mapping table by bilinear interpolation

3 实验结果

为了验证本文提出方法的有效性，采用了一个含有枕型畸变的正交网格图作为待矫正图像，采用本文的方法对其进行矫正，其结果如图7 所示。从结果可以看出，相较于图7(a)中含有枕型畸变的正交网格线，经过本文方法矫正后的图像效果改善明显，说明了本文提出的方法能够很好地对图像畸变进行矫正。

为了进一步说明通过压缩逆向映射表来提高算法性能后对矫正结果的影响，本文在MATLAB上实现了逆向映射表（分辨率为640×480 像素）的压缩，n的值取4、8、16 和32，然后利用经双线性内插法在线重建的逆向映射表对一幅含桶型畸变的图像进行矫正，矫正效果如图8 所示。

图7 带有枕型畸变的正交网格图矫正结果Fig.7 Correction result of orthogonal grids with pillowtype of distortion

图8 矫正效果对比Fig.8 Comparison of correction effect

图8(a)的图像是一幅由摄像头采集的含有桶型畸变的原始图像。图8(b)中图像为使用不经压缩的逆向映射表进行矫正后所得的图像。对比8(a)和8(b)可以明显观察到经过矫正后图形中的桶型畸变已经消失，标定板的边缘已经由外凸变为水平，说明该矫正算法能够很好地对畸变图像进行矫正。

另外，对比图8(a)、8(c)、8(d)、8(e)几幅图片可以发现，当通过对参数n分别取n=4、n=8、n=16 时对逆向映射表进行压缩之后，使用本文中的算法对图像畸变进行矫正，其结果也较为理想。在图8(c)、8(d)、8(e)中桶形畸变都被明显矫正，且矫正后的图像效果清晰，证明了可以通过压缩逆向映射表的方式在得到清晰图像的同时节省FPGA 的硬件资源，并减小算法复杂度。

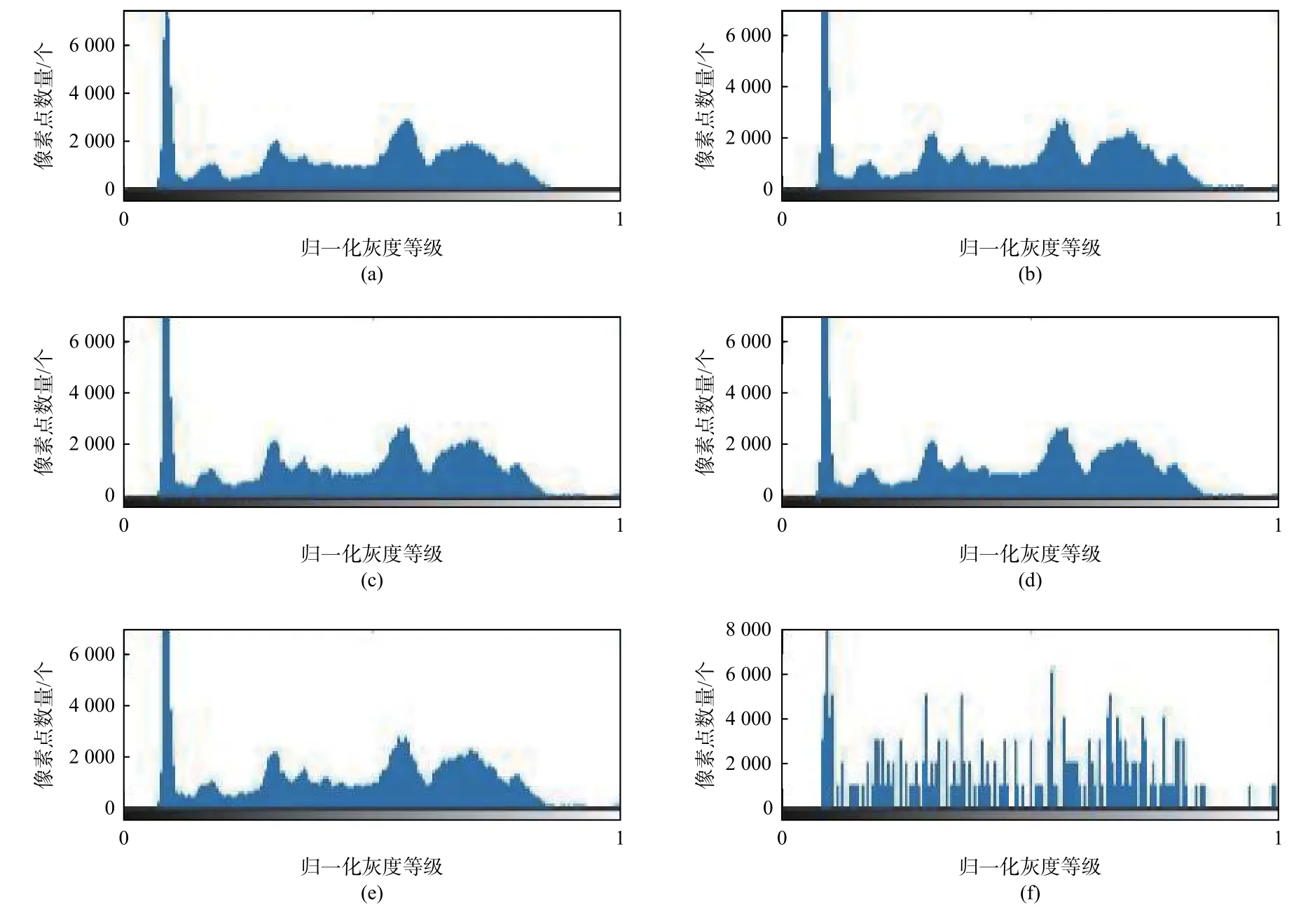
图9 灰度直方图Fig.9 Gray histogram

值得注意的是，在图8(f)中，当n=32 时图像出现了严重的失真。为了对该结果进行分析，绘制了图8 中图像的灰度直方图，如图9 所示。通过观察图9 中的直方图可以发现，由于畸变矫正只是矫正了图像的部分信息，矫正前后图像的基本特征是一致的。因此，畸变图像与经过有效矫正后的图像拥有近似的灰度直方图分布。但是当n=32时，矫正后图像的像素分布已经严重偏离原始图像，出现了马赛克现象，细节严重丢失。

为了分析压缩图像映射表对于矫正后图像的影响情况，以图8(b)中的图像作为标准图像，分别计算8(c)、8(d)、8(e)、8(f)中图像与8(b)中图像的PSNR 与SSIM。以此来衡量图像质量的变化情况，结果如表2 所示。

表2 中，当PSNR 高于40 dB 时，说明图像非常接近标准矫正图像，质量非常好；低于20 dB 时，说明图像质量很差，已不可接受。而SSIM 值越高，则表明图像失真越小。

由上述的仿真结果可知，适当降采样后的逆向映射表可以很好地实现图像畸变矫正，能够在保证图像清晰度的情况下将逆向映射表压缩为原来的1/16。但通过对逆向映射表进行降采样再利用插值重建并不能无限制地减小其分辨率，其分辨率的大小取决于逆向映射的平滑度和重建所需的精度。

表2 利用经压缩的逆向映射表矫正畸变图像的PSNR 和SSIMTable 2 Correction of PSNR and SSIM of distorted image using compressed reverse mapping table

通过搭建FPGA 双目视觉采集系统，验证本文算法的硬件可实现性。选用Intel FPGA Cyclone IV 系列EP4CE115F29C7 芯片作为图像采集及预处理系统的核心，如图10 所示。使用两颗CMOS 图像传感器进行采集，并在板上通过本文算法进行处理。输出结果显示，采用本文算法后，能够使得图像畸变得到矫正，提高图像质量以满足后续图像处理的需求，如图11所示。

图10 FPGA 双目视觉采集系统Fig.10 Binocular vision acquisition system based on FPGA

图11 双目视觉采集系统效果图Fig.11 Effect diagram of binocular visual acquisition system

4 结论

为了提高矫正含畸变图像的实时性，本文研究了如何在FPGA 上实现畸变矫正算法。针对FPGA 实现图像畸变矫正算法时，存在在线计算逆向映射坐标复杂和片上ROM 容量不够的问题，对图像畸变矫正算法进行了优化，即通过查找逆向映射表和对逆向映射表进行降采样再利用插值重建，降低了在线计算量和片上ROM 的容量需求。实验结果表明，在合适的分辨率下，优化后的畸变矫正算法具有良好的矫正效果，并具有广泛的实际应用价值。