基于改进CEEMDAN⁃熵方法的管道泄漏工况识别

李传宪，逯雯雯，石亚男，杜世聪，郑琬郁，李鹏宇

管道运输具有输量大、成本低、受环境影响小的优点，在石油天然气行业有着越来越重要的作用。管道腐蚀、施工破坏，以及人为破坏等因素使管道频繁发生泄漏，造成了严重的人员伤亡、巨大的财产损失和环境破坏[1]，因此提高输油管道泄漏检测的准确性十分必要。目前常用的输油管道泄漏检测方法主要有光纤检测法、实时模型法及负压波法[2]，其中负压波法具有精度高、投资少、原理简单的优点，应用最为广泛。在管道泄漏检测中，现场往往存在各种不同工况操作引起的干扰以及传感器本身的噪声干扰等，都会导致负压波的信噪比较低，进而影响管道泄漏检测的准确性。

针对管道泄漏引起的负压波信号的去噪研究，小波分析[3]和EMD分解[4]都是常用的方法，然而小波分析不具有自适应性，需要选择合适的小波基函数和阈值函数[5]，EMD分解方法虽然具有自适应性，但是分解过程会造成模态混叠和端点效应[6]，针对这一问题，本文提出了改进的添加成对白噪声的完全集合经验模态分解算法（改进的CEEMDAN）对负压波信号进行预处理，该方法不仅具有自适应性，克服了模态混叠，而且消除了辅助白噪声，提高了运算效率，使噪声信号和泄漏信号可以更好的分离开，提高了负压波信号的去噪效果。针对管道不同工况下信号的特征提取，能量特征[7⁃9]和峭度特征[10]常用于正常运行、泄漏以及调泵等差别较大工况的特征描述，而不适用于差别较小工况的特征描述，为了全面表征管道不同工况的压力信号特征，本文提出了基于熵的特征向量提取方法，计算负压波信号的能量熵、峭度熵以及排列熵，从能量、峭度、时间序列复杂性三个角度全面提取不同工况下的信号特征，并第一次将排列熵应用到管道不同工况的识别中。

1 EMD、EEMD与 CEEMDAN方法介绍及仿真模拟

1.1 EMD及EEMD方法

经验模态分解（EMD）是希尔伯特黄变换(HHT)方法的关键部分，它依据信号自身的时间尺度特征进行分解，而不依赖于任何基函数，具有自适应性[11]。EMD的实质是按照时间尺度由小到大的顺序把不同频率的分量逐步从原始信号中分离出来的过程，得到不同频率的分量称为固有模态分量(IMF)[7]。

原始信号x(t)经EMD分解后可表示为:

式中，IMFi(t)为包含不同时间尺度的固有模态分量，r(t)为残余分量，N为固有模态分量的个数。

实际检测到的信号具有复杂性，当信号中出现间断或跳跃性变化时，传统EMD分解无法将具有不同特征时间尺度的成分完全分离开来，会使不同时间尺度的信号出现在同一分量中，产生模态混叠现象，进而导致各IMF失去原来的物理意义。集合经验模态分解（EEMD）利用白噪声功率谱密度均匀分布的特点，引入辅助白噪声，在一定程度上削弱了模态混叠现象[12]。

EEMD的步骤为：

（1）在原始信号x(t)中添加标准差为kε的零均值白噪声 n(t)，得到混合信号 x（t）+kεn（t），其中，ε为原始信号的标准差，k为白噪声幅度系数。一般k取0.01～0.50较合适，经过大量实验，本文取其为0.20。

（2）利用EMD对上述混合信号进行分解。

（3）每次加入不同的n(t)，重复步骤（1）、（2）。

（4）最后计算同一特征时间尺度的所有分量的均值- -- --------IMFi(t)，并将其作为最终的IMFi(t)。

1.2 CEEMDAN及其改进算法

EEMD通过多次加入白噪声求均值的方法，在一定程度上减少了模态混叠现象的产生，但是加入的白噪声所带来的误差不会因为求均值的过程完全消除，并且随着重复加入白噪声次数的增多，导致运算量大大增加。针对这个问题，引入添加自适应白噪声的完全集合经验模态分解（CEEMDAN）[13⁃14]。

利用EMD进行分解得到的第i个模态分量用imfi()表示，利用CEEMDAN方法分解所得到的第i个模态分量记为- -- -- ------IMFi(t)，那么 CEEMDAN方法步骤如下：

（1）CEEMDAN方法第一个固有模态分量的获得与EEMD算法相同，即对混合信号x（t）+kεnj（t），j=1，2，…，M进行分解，并保留M次分解的第一个固有模态分量，将所得到的分量取平均值，作为CEEMDAN方法的第一个固有模态分量。

（2）白噪声经EMD分解得到的模态分量表示为imfi(kεnj(t))，将其与上一步计算得到的残余信号组合得到混合信号为 ri(t)+imfi(kεnj(t))，i=1。利用EEMD对得到的混合信号进行分解，保留每次分解的第一个固有模态分量，取平均值可以得到CEEMDAN方法的第二个固有模态分量。

（3）继续利用步骤（2）的算法对残余分量进行分解，可得第n+1个固有模态分量及其残余分量为：

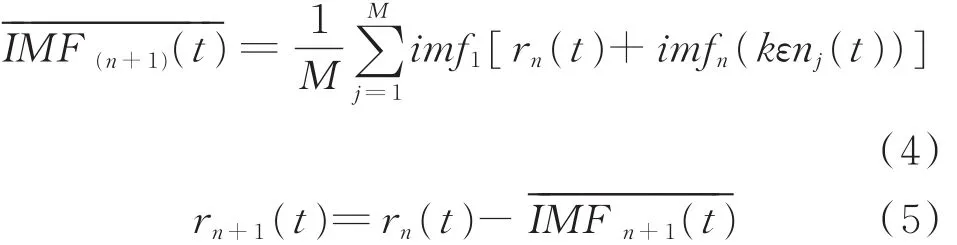
（4）当残余分量满足终止条件时，算法终止。

在CEEMDAN的算法步骤中可以发现，多次利用了EEMD方法计算每阶模态分量。在求得每阶固有模态分量时仍然需要重复大量运算以消除添加白噪声的影响，并且添加的白噪声很难被完全消除。针对这种现象，提出添加成对白噪声的方法，也就是将所加的每个噪声都采用正负成对的形式添加到信号中，如式（6）所示：

式中，S是原始信号；N是添加的白噪声；M1是原始信号和正噪声形成的混合信号；M2是原始信号和负噪声形成的混合信号。

通过添加成对白噪声进行辅助的方法，每添加一次白噪声所得到的固有模态分量中，其中一部分包含了正噪声的残余量，另一部分包含了负噪声的残余量，在利用均值求最终的固有模态分量时，大部分噪声会正负抵消，这样可以在运算量较少的情况下，较精确的去除添加辅助噪声的影响。

1.3 仿真模拟

以模拟信号为例对以上几种方法进行验证，对余弦信号x(t)=2cos(20πt)加入间歇性高频振荡信号，采样点数为2 000，得到如图1所示波形。

图1 合成模拟信号Fig.1 The synthetic analog signals

分别利用EMD、EEMD、CEEMDAN方法和改进的CEEMDAN方法对上述合成模拟信号进行分解，其中EEMD、CEEMDAN和改进的CEEMDAN三种方法都加入幅度系数为0.20的白噪声运算100次，得到如图2所示的4种方法分解结果。从图2（a）中可以发现，经典EMD方法无法完全把高频分量和低频分量分离开，出现了严重的模态混叠现象。而图 2（b）、（c）、（d）基本上都把高频分量和低频分量分离开了，说明EEMD、CEEMDAN和改进的CEEMDAN三种方法基本上消除了模态混叠现象。分别将EEMD、CEEMDAN和改进的CEEMDAN分解后的各个IMF分量重构，并计算原始信号能量与重构后的信号能量，Eo=4.040 7×103， EEEMD=4.043 8×103， ECEEMD=4.040 7 × 103，E改CEEMD=4.040 7× 103。发现EEMD的重构信号引入了很多噪声，重构信号的能量与原始信号的能量差别较大，影响后续处理，而CEEMDAN和改进的CEEMDAN几乎不引入噪声，重构信号的能量与原始信号的能量一样，保证了算法的完备性。

图2 四种方法对图1复合信号的分解结果Fig.2 The decomposing results of Fig.1 composite signal by four methods

对比图2（c）、（d）可以发现，CEEMDAN分解得到的前4个IMF分量以噪声为主，无法识别出其中的高频分量，而经过改进的CEEMDAN分解后，前4个IMF分量包含的噪声比较少，从第4个IMF分量开始已经明显包含高频振荡分量，并且IMF 5、IMF6分量的光滑性更好，说明加入成对噪声的方法，既可以克服模态混叠，又能消除大量噪声。对比CEEMDAN及改进的CEEMDAN方法计算每阶IMF分量的迭代次数，如图3所示，图中蓝色盒子里的红色短线代表迭代次数的中位数，而红色的“+”表示偏离中位数较大的点，其位置越靠上代表迭代次数越多，运算时间越长，可以发现改进的CEEMDAN方法的迭代次数明显降低，运算效率大幅提高。综合以上分析，改进的CEEMDAN方法，在克服模态混叠，消除辅助白噪声和提高运算效率三个方面明显好于其他三种方法，因此本文选择改进的CEEMDAN方法进行后续处理。

图3 CEEMDAN方法改进前后迭代次数Fig.3 Iteration times of CEEMDAN method and impr oved CEEM DAN method

2 现场数据中的应用

实验以西部某输油管线为研究对象，输油管线长52.6 km，管径557 mm，设计压力8 MPa。压力传感器安装在管线两端。在实验中，采取人工下油的方式模拟泄漏，将管道首末两端采集到的负压波信号作为检测对象。为了区别泄漏与其他正常工况操作引起的负压波，分别对切罐、切泵等工况引起的负压波进行采集，进行分析处理。对不同工况下的数据进行统一，下文所有用到的负压波信号数据均采用了式（7）进行标准化处理：

式中，x(t)代表原始信号；x′(t)代表标准化以后的信号；min(x(t))代表原始信号的最小值；max(x(t))代表原始信号的最大值。不同工况的时域波形如图4所示。

图4 泄漏、切罐、切泵三种不同工况下的时域波形Fig.4 Waveforms of leakage,cutting tanks and cutting pumps

2.1 信号预处理

除了不同的工况操作会对泄漏的识别产生干扰以外，现场环境噪声以及获取信号的软硬件设备的噪声都会导致采集到的负压波信噪比较低，影响泄漏工况的识别精度。因此需要对采集到的负压波信号进行去噪预处理，以提高工况识别准确性。

改进的CEEMDAN可以有效抑制模态混叠现象，并且可以最大程度地降低外加白噪声对信号分解的影响，但是实际管道泄漏信号中包含了大量的噪声，只有提取主要包含泄漏信号的分量即有效IMF分量，去除噪声影响，才能最大程度得到有意义的特征值。管道一旦发生泄漏，其产生的负压波会同时向管道上下游传播，本文提出利用管道上下游的两路信号进行相关分析的方法来提取有效IMF分量。在管道上下游采集到的负压波信号中，既包含泄漏信号又包含噪声信号，但是只有泄漏信号具有相关性，而噪声信号互不相关。利用这一规律，将一路信号分解得到的IMF分量分别与另一路信号进行相关分析就可以提取含有泄漏信号的有效分量[15]。

以一次实验获得的泄漏负压波信号为例进行分析，图5所示分别是管道上下游采集到的压力信号x1（n）和x2(n)。图6所示的IMF分量图是利用改进的CEEMDAN对上游负压波信号x1(n)进行分解得到的，可以发现前5个IMF分量以噪声为主，第6个IMF分量及以后包含的噪声明显减少，但是哪些是有效IMF分量不能进行明确判断，因此需要进一步分析。

分别计算各个IMF分量与x1(n)和x2(n)的相关系数，得到表1，表中r表示原始信号经过分解得到的最终残余分量。从表1可以发现，IMF 1和IMF2与x1(n)的相关系数明显偏低，而IMF3-IMF9与x1(n)的相关系数差别不大，这可能是因为IMF3-IMF9中包含了与x1(n)相关性较大的噪声部分，因此无法辨别哪些是相关分量，而IMF1-IMF5与x2(n)的相关系数较其他明显偏低，并且与图7所示的信息相吻合，因此前5个IMF分量以噪声为主，是应当去除的不相关分量，而IMF6-IMF11是应当与残余分量一起参与重构的有效分量。

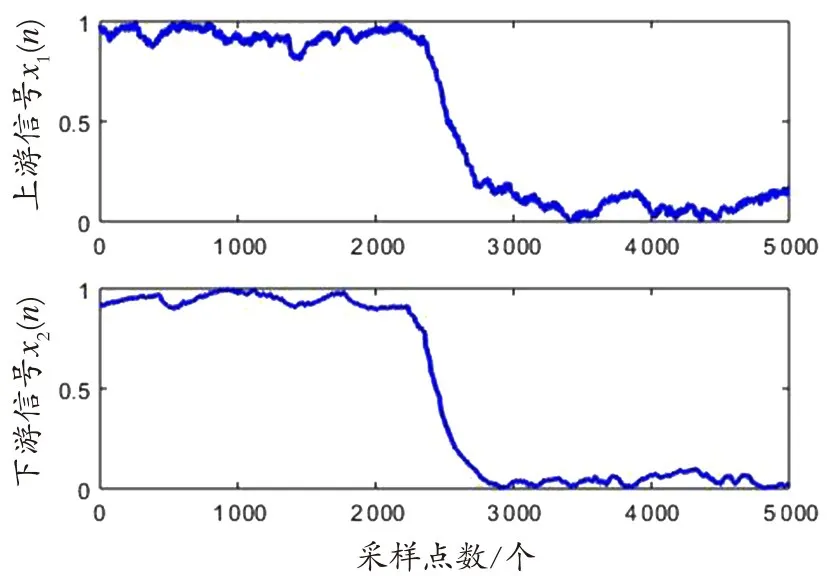
图5 管道上下游采集到的负压波信号Fig.5 Negative pressure wave signals collected fr om upstream and downstream pipes

图6 上游负压波信号的IMF分量图Fig.6 IMF components’diagrams of upstream negative pr essur e wave signal

2.2 特征向量提取

准确的特征向量提取可以大大提高输油管道泄漏检测的准确性。本文提出了基于熵的特征提取，Shannon提出的信息熵[16]是衡量系统随机性的指标，信息熵越大代表系统的随机性越大。系统X包括多个事件 X={x1，x2，…，xn}，并且事件发生的概率为 P={p1，p2，…，pn}。那么事件所携带的信息量：I(xi)=-pilg pi，全部事件的信息量累加为系

表1 各个IMF分量分别与x 1(n)和x2(n)的相关系数Table 1 Correlation coefficients between IMF components and x1(n)/x2(n)

当管道发生泄漏时，其负压波信号所携带的能量与其他工况相比有很大的差异性，并且在不同的频率段中能量分布情况会发生变化。因此，本文利用能量熵对管道泄漏工况进行识别。经过2.1信号预处理，已经获得了有效IMF分量，然后对其提取能量熵，其步骤如下：

（1）分别计算各个有效IMF分量的能量：

式中，N为信号的采样长度；xi为信号的幅值。

（2）计算有效IMF分量的能量总和：

式中，m为有效IMF的个数。

（3）用单个IMF的能量占总能量的比例作为其概率，按照Shannon信息熵的形式计算每个样本的能量熵：

图7所示为泄漏、切泵、切罐的22个样本的能量熵。

图7 泄漏、切泵和切罐的22个样本的能量熵Fig.7 Energy entropy of 22 samples of leakage,cutting pumps and cutting tanks

由图7可以发现，切泵产生的负压波的能量熵小于泄漏和切罐产生的负压波的能量熵，但是泄漏和切罐的能量熵没有明显区别。因此，能量熵可以一定程度上描述三种工况的负压波的特征，但是不够全面。

管道发生泄漏时，产生具有显著冲击特点的负压波。峭度可以描述信号的冲击特性，但是峭度值一般只能用来判断有没有泄漏发生，而不能用来区分其他工况。因此本文仿照能量熵提出了峭度熵的概念，既可以突出峭度对冲击信号灵敏度高的特点，又能考察不同频率下的冲击特性。峭度熵的求解过程如下：

（1）分别计算各个有效IMF分量的峭度：

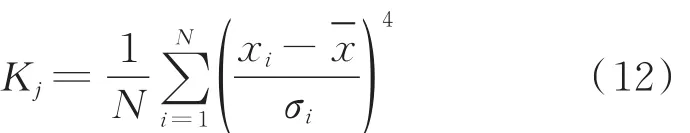
式中，xi为信号的幅值，为信号的均值，σ为信号的标准差，N为信号的采样长度。

（2）计算有效IMF分量的峭度总和：

式中，m为有效IMF的个数。

（3）将单个IMF的峭度占总峭度的比例作为其概率，按照Shannon信息熵的形式计算每个样本的峭度熵：

图8为泄漏、切泵、切罐的22个样本的峭度熵。

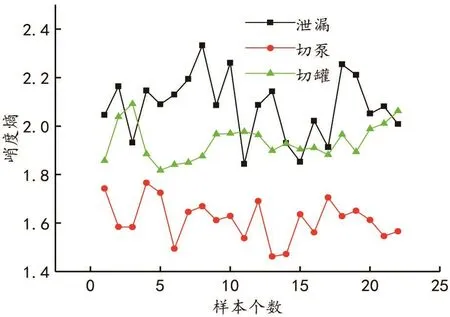
图8 泄漏、切泵和切罐的22个样本的峭度熵Fig.8 Kurtosis entropy of 22 samples of leakage,cutting pumps and cutting tanks

由图8可以发现，切泵产生的负压波的峭度熵最小，泄漏产生的负压波的峭度熵最大，而切罐产生的负压波的峭度熵处于中间大小，因此峭度熵可以在一定程度上用于三种工况的模式识别。

排列熵[17⁃18]（PE）不同于上文所述的能量熵和峭度熵，它是时间序列的复杂度的评价指标，其值越大，时间序列的复杂度越高，而且它对时间序列的突变现象具有很高的敏感性。输油管道发生泄漏或者进行其他工况操作时，压力波往往会发生突变现象，因此可以用排列熵表征不同工况的特征。其求解过程如下：

（1）将2.1中得到的有效IMF分量与残余分量一起重构得到新序列{s(n)，n=1，2，…，N}。

（2）对新序列进行相空间重构时，采用互信息法确定最优时延τ为17，采用伪近邻法[19]确定最优嵌入维数m为2，得到重构序列Xj=[s(j)，s(j+τ)，…，s(j+(m-1)τ)]， 其 中 下 标 j=1，2，…，N-(m-1)τ。

（3）以重构序列Xj为行向量构造矩阵X，并对矩阵X的每一行向量进行升序排列，得到s[j+(j1-1)τ]≤ s[j+(j2-1)τ]≤ … ≤ s[j+(jm-1)τ]。其中 j1，j2，…，jm表示重新排列后各个元素所在列的下标，是一组符号序列。

（4）矩阵X的每一行向量，经过重新排列后都可以得到一组符号序列 S（g）=（j1，j2，…，jm）。其中g=1，2，…，l，l≤ m!。统计每一组符号序列出现的次数，进而可以计算出每一种符号序列出现的概

（5）仿照Shannon熵的形式，定义时间序列{s(n)，n=1，2，…，N}的 PE为：

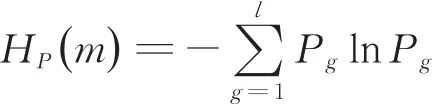
图9为泄漏、切泵、切罐的22个样本的排列熵，可以发现，泄漏产生的负压波的排列熵明显小于切泵和切罐产生的负压波的排列熵，而切泵和切罐产生的负压波的排列熵几乎重合。这说明，排列熵可以用于泄漏工况的识别，而对于其他工况的识别效果不好。

2.3 工况识别

2.2 中提出基于熵的特征提取，分别对能量熵、峭度熵、排列熵进行了研究，将能量熵、峭度熵、排列熵作为特征向量，可以全面刻画不同工况产生的负压波的特性，利于后续的模式识别，分别以三种工况下的一组信号为例展示特征向量如表2所示。由于支持向量机（SVM）适用于小样本数据的分类[20⁃21]，而现场实际输油管道能提供的泄漏样本很少，因此选用支持向量机具有较好的分类精度。构造两个支持向量机分类模型，分别用于区分泄漏和切罐，泄漏和切泵，将其命名为SVM 1和SVM 2。SVM 1输出值为1表示泄漏，-1表示切罐；SVM 2输出值为1表示泄漏，-1表示切泵。其中每种工况的22个样本用于训练模型，另外22个样本用于测试模型的分类效果。

图9 泄漏、切泵、切罐的22个样本的排列熵Fig.9 Permutation entropy of 22 samples for leakage,cutting pumps and cutting tanks

表2 改进的CEEMDDAN分解三种工况的特征向量Table 2 The eigenvectors of three working conditions decomposed by improved CEEMDDAN method

利用改进的CEEMDAN和EEMD方法分别对原始负压波信号进行分解，然后求其有效IMF分量的能量熵、峭度熵以及排列熵，利用支持向量机对三种工况进行分类，得到表3。

表3 改进的CEEMDAN⁃SVM（C⁃S）和EEMD⁃SVM（E⁃S）诊断结果Table 3 Diagnostic results of improved CEEMDAN⁃SVM(C⁃S)and EEMD⁃SVM(E⁃S)

由表3可知，改进的CEEMDAN得到的分类结果均为100%，而EEMD对于泄漏和切泵的分类准确率较高，但是对泄漏和切罐的分类准确率较低，说明本文改进的CEEMDAN方法效果较好。

为了验证所选特征向量的有效性，在利用改进的CEEMDAN分解后，分别单独利用能量熵和峭度熵，能量熵和排列熵，峭度熵和排列熵对三种工况进行分类得到表4。由表4可知，能量熵和峭度熵对泄漏和切泵的识别效果较好，对泄漏和切罐的识别效果较差，说明其对不同工况的适应性较差；能量熵和排列熵组合的工况识别结果均较差，峭度熵和排列熵组合的工况识别效果较好，但仍然不如能量熵、峭度熵和排列熵组合的诊断效果好，说明本文提出的特征向量可以全面描述不同工况的负压波特性，具有较强的适应性。

3 结 论

分别对EMD、EEMD、CEEMDAN和改进的CEEMDAN方法进行仿真模拟，并对现场实际输油管道不同工况下的负压波信号进行预处理，选用不同的特征向量进行分类。得到以下结论：

（1）通过对4种方法的仿真模拟研究发现，改进的CEEMDAN方法能有效抑制模态混叠，消除噪声，信号所包含的信息可以比较真实的通过IMF的特征来反映。将改进的CEEMDAN应用于输油管道泄漏检测中，发现基于改进的CEEMDAN的管道泄漏识别方法比基于EEMD的泄漏识别方法准确率更高。

（2）提出基于熵的特征向量，通过对不同特征向量的模式识别效果进行对比，发现能量熵、峭度熵、排列熵作为不同工况的特征向量可以全面地反映不同工况的特征信息，比任何单独两种熵组成的特征向量效果更好，对不同工况具有更强的适应性。