用赫尔德不等式和柯西不等式证明一类根式不等式
刘保乾
(西藏自治区组织编制信息管理中心,西藏 拉萨 850000)
用赫尔德不等式和柯西不等式对根式不等式进行证明是比较常见的做法,通常是用赫尔德不等式和柯西不等式得到根式表达式的一个估计,然后用这个估计式对欲证不等式进行放缩,从而达到证明不等式的目的.但实际上这只能证明一些较简单的不等式,对多数根式不等式直接证明会失效,此时得另想办法.本文借助于不等式自动发现与判定程序agl2012[1-3]对此问题进行探讨,提出了试探性解决算法并编写了应用程序,解决了大量不等式难题和遗留问题.
1 赫尔德不等式和柯西不等式
赫尔德不等式,又称为Hölder-Rogers 不等式,是指:设aij(i=1,2,…,n,j=1,2,…,m)是正实数,αi(j=1,2,…,m)是正实数,且α1+α1+…+αm=1,则

当(a11,a21,…,an1),(a12,a22,…,an2),…,(a1m,a2m,…,anm)成比例时取等号.当 m=n=3,时,就有下面的特例.
推论设 xi,yi,zi>0(i=1,2,3),则有
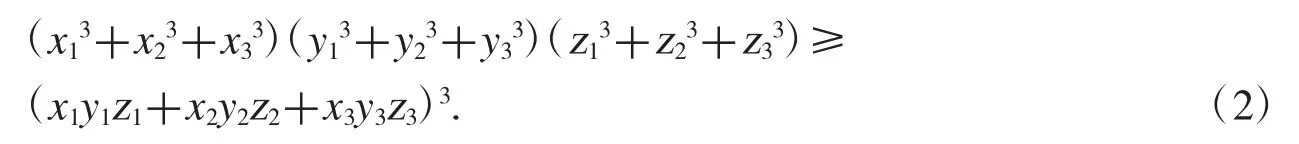

本文中主要应用(2)式和(3)式.
2 算法和程序
2.1 基于赫尔德不等式的算法
设 Ai,Bi>0(i=1,2,3),对于根式型不等式

由赫尔德不等式得
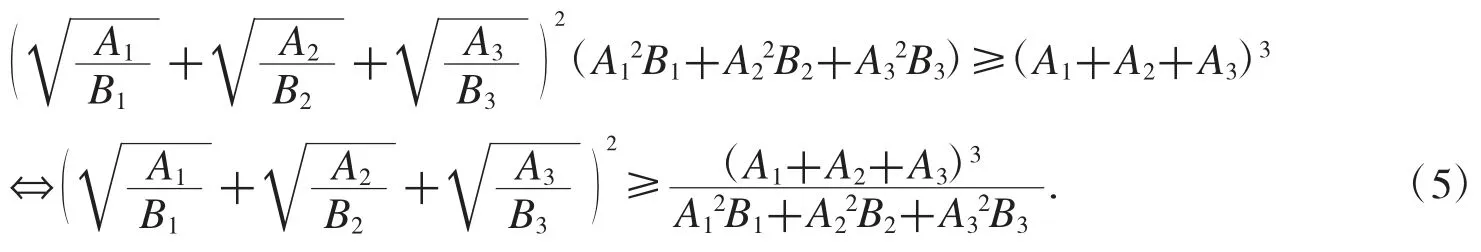
如果不等式

成立,则不等式(4)获证.如果不等式(6)不成立,此时可以通过给有关项乘以附加表达式的方法加以解决.例如,可以引入附加表达式Ci(i=1,2,3),由赫尔德不等式得

如果不等式
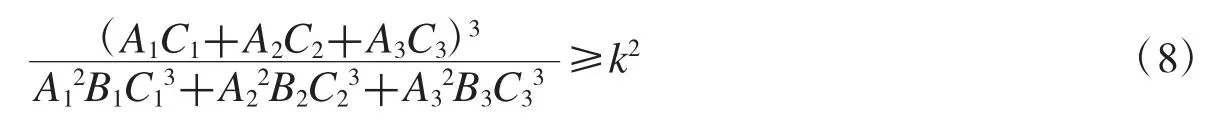
成立,则引入附加表达式成功,即要证根式不等式(4),只需证明不等式(8)成立就可以了.
或者引入附加表达式Ci(i=1,2,3),由赫尔德不等式得

故欲证根式不等式(4),只需证明不等式

而且不等式(8)或(9)的次数愈低,则认为引入的附加表达式愈理想.为叙述方便,以下称不等式(4)为欲证式,不等式(8)和不等式(9)为需证式.
由此可见,证明不等式(4)的关键是寻找附加表达式Ci,使需证式(8)或(9)成立,而这种寻找工作可以通过agl2012 程序的数据构造命令构造海量数据实现.调用agl2012程序的随机数验证模块otf 进行测试,找出满足(8)式或(9)式的附加表达式Ci.而且还可以在找到的附加表达式结果中,选出那些使需证式次数最低的附加表达式,从而得到最简洁的证法.根据这个思路可直接得到一个试探性验证算法,并编写出应用程序hldset.其命令格式为:
>hldset(ex,k,setj);
当setj 取为集合{1}时,表示附加表达式取为C1=C2=C3=1,此时(8)式退化为(6)式,表示不等式(4)可以直接用赫尔德不等式证明.
注1在实际编程时,可将待测试数据集setj 取为一个多项式通式,例如对于3 元4次多项式,这个通式可取为

然后设定系数ki在一定的范围内取值,用所得的多项式作为附加表达式逐一验证.如果验证不成立,再升高次数继续验证.
注2对于开3 次方甚至开n 次方的根式,算法是一样的.例如对根式不等式
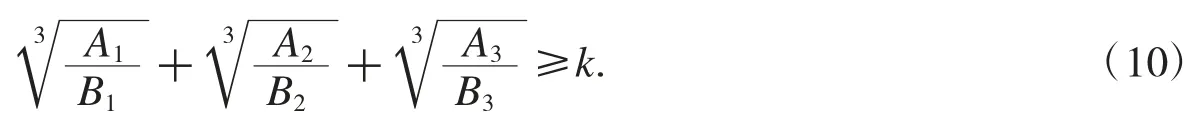
其需证式为
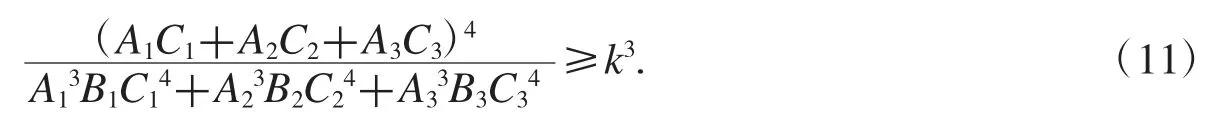
注3对于不等式(4),还有一些变式,利用这些变式的特点,就可能得到次数更低的不等式.例如,对不等式
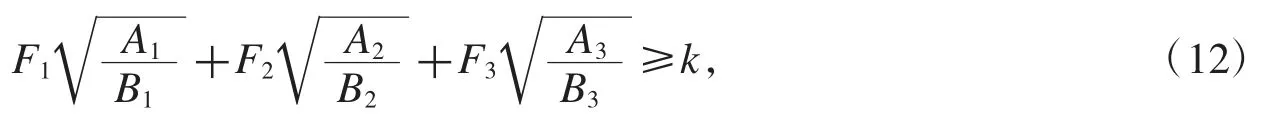
此时需证式可取为

即实际编程中要综合考虑各种可能的情形,以覆盖尽可能多的类型,以增加程序功能.
2.2 基于柯西不等式的算法
观察不等式(4)可以发现,它是下界型不等式.那么对于上界型根式不等式
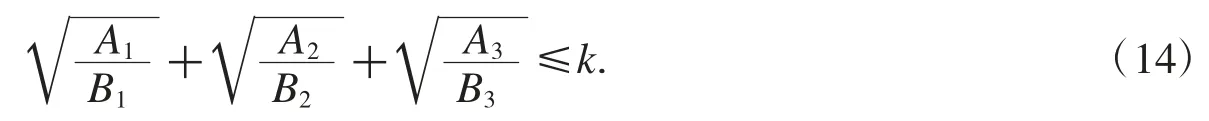
该如何破解根号呢?可以考虑用柯西不等式来解决.
对于不等式
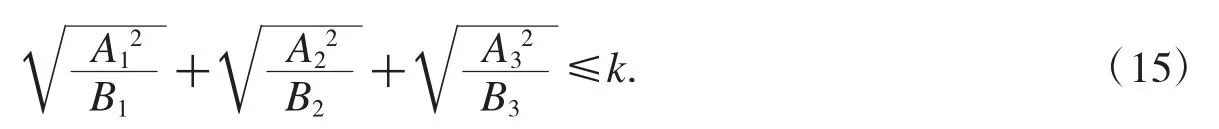
(注意不等式(14)总是可以化为(15)的形式),若引入附加表达式W={W1,W2,W3},由柯西不等式有

成立,则不等式(15)获证.
对于不等式(14),若引入附加表达式W={W1,W2,W3},由柯西不等式有

成立,则不等式(14)获证.由此得到证明不等式(14)的算法和程序.现用csset 表示这个算法和程序,其命令格式为:
>csset(ex,k,setj);
本文重点关注需证式的建立过程,尤其是附加表达式的寻找过程.由于需证式本质上是一个多项式不等式,而多项式不等式的证明目前已有多种证法可以选择,故需证式的证明不作为讨论重点.
3 应用举例
例 1(陈计,https://artofproblemsolving.com/community/c6h202843)设 x,y,z>0,证明不等式

其中Σ表示循环求和(以下均同于此).
证明不等式(18)已被陈计证明,他实际上引入了附加表达式

为了书写简便,可以对附加表达式进行简写,如这里的附加表达式可简写
为C={2x+y+z}.现用hldset命令进行测试.键入命令:
>read“zk.txt”;#调用提前构造好的数据集#
>hldset(sqrt((x^2+y z)/(y^2+z^2+y z)),sqrt(6),zk);
则输出一系列附加表达式及对应的需证式,以下用deg 表示需证式的次数.
具体输出结果如下:

可以看出,陈计所取的附加表达式最理想,对应的需证不等式为

次数为9 最低,且用配方法容易证明.
如果以(9)式为算法公式,则附加表达式可取为C=2x2+yz,需证式为

此时deg=12.
例22008 年,网友can_hang2007(越南著名不等式专家)在AoPS 上发布了主题为“hard cyclic inequality,I created it but I cannot solve it”的帖子:设 x,y,z>0,证明不等式

证明不等式(19)至今未见到解决.但用hldseta 命令很快找出附加表达式为C={x+2z},此时需证式为

不等式(20)可化为一个3 元11 次轮换对称多项式不等式,用agl2012 程序的配方命令容易证明.
如果按(12)式对应的算法做,则需证式为

此时deg=8,证明自然要容易的多.
注4找到理想的附加表达式,使需证式的次数最低,这是解题过程中追求的一个目标,但却没有捷径,只有逐个命令去验证.
例 3设 x,y,z>0,证明不等式(https://artofproblemsolving.com/community/c6t243f6h 1116690_xyzgt0hard_and_stronger)

证明在原贴中,网友Crazy_LittleBoy 给出不等式(21)的一种证明.其实用hldset 命令可找到附加表达式C=2x2+5xy+5xz+yz,此时需证式为

deg=9,用多种方法可以证明.
例 4设 x,y,z>0,x+y+z=1,证明不等式
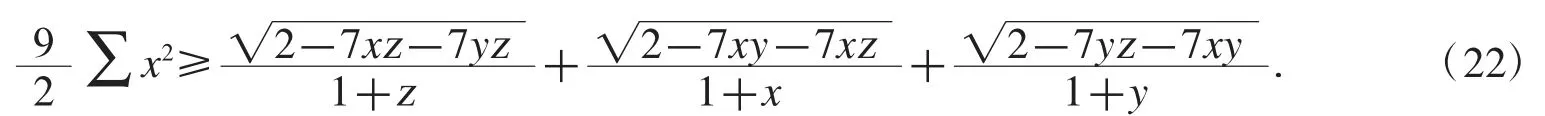
证明用csset 命令求出附加表达式可取为2x2+2y2+z2+2xy.由柯西不等式,要证(22)式,只需证
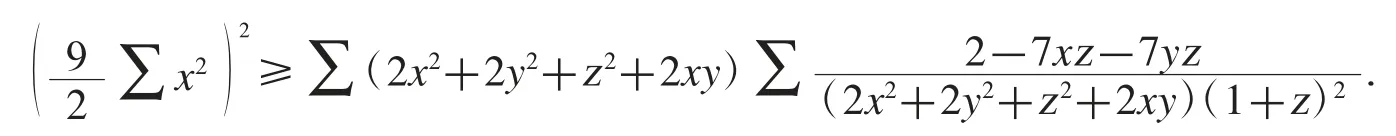
利用条件x+y+z=1 对这个不等式齐次化后,得到一个3 元16 次完全对称多项式不等式,且是差分代换平凡的,由此得证.
例 5ΔABC 中,有不等式(Hcx19,见文献[4])

证明将不等式(23)代数化,得等价式

由hldset 命令找出附加表达式为C={x+2y+2z},deg=21.
在(23)式的证明过程中,虽然得到的需证式次数高达21,但用差分代换方法(参阅文献[5]和文献[6])则容易证明,而不等式(23)本身是一个难度很大的不等式,用其它方法是很难证明的.
例6在ΔABC 中,证明不等式

证明 不等式(24)等价于代数不等式

取附加表达式为C={8x+y+z},则需证式为
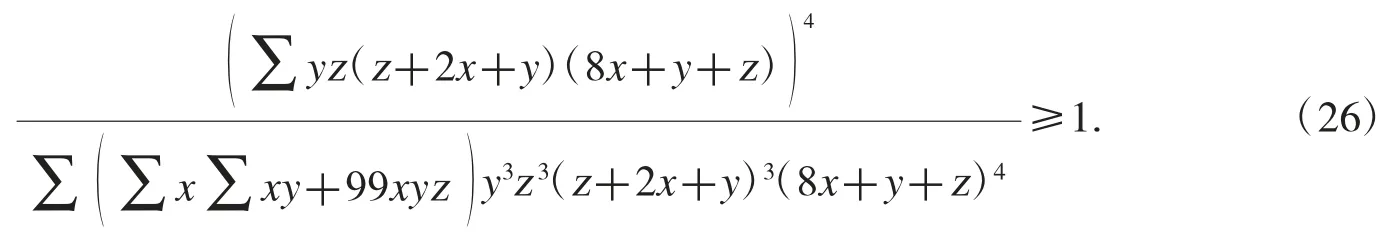
设 x=s-a,y=s-b,z=s-c,其中 s 是 ΔABC 的半周,此时(26)式等价于

用agl2012 程序可以很快给出bds 的非负分拆式,故不等式(24)获证.
例 7设 x,y,z>0,证明不等式

证明由命令csset 得到附加表达式为y+9z+2x,此时需证式为

这个不等式并不容易证明.但如果取附加表达式为W=yz+xy+xz+x2,则由柯西不等式,只需证

由于这是基本不等式的形式,立刻就获得了证明.
注5例7 给我们的启发是:同样是用柯西不等式证题,选用的附加表达式不同,使用柯西不等式的方式不同,效果大不一样.问题是,我们能否预先设出附加表达式的具体形式,然后通过待定系数的方法得到基本不等式的形式,或者其它我们希望得到的可以获得证明的形式,这才是一个值得重视的研究思路和方向.
例 8设 a,b,c,d>0,证明不等式

证明这是一个四元不等式,其算法和程序与三元的完全类似.由四元的程序hldset4可找出附加式为 C={bd+c(b+d)},需证式为

不等式(29)取分母后是一个4 元15 次对称多项式不等式,易用差分代换方法证明,从而不等式(28)获证.
4 agl2012程序证明功能补述
不等式自动发现与判定程序agl2012 的主要功能是自动发现不等式,其实它的判定证明功能也有不少,这里专门介绍如下:
1.用差分代换方法证明锐角三角形中的不等式,见文献[7];
2.配方(参阅文献[8-10]);
3.s-R-r 非负分拆证明(参阅文献[11]);
4.寻找已知不等式的局部对称式;
5.诱导解法;
6.用hldset 和csset 等命令辅助证明根式不等式,如本文中的诸例.
上述功能说明,agl2012 程序不仅是一个自动发现系统,而且也是一个判定和证明系统,是一个教学和研究应用辅助平台,极大地方便了各种应用.下面围绕agl2012 程序的诱导解法功能举两个例子.
例 9设 x,y,z>0,证明不等式
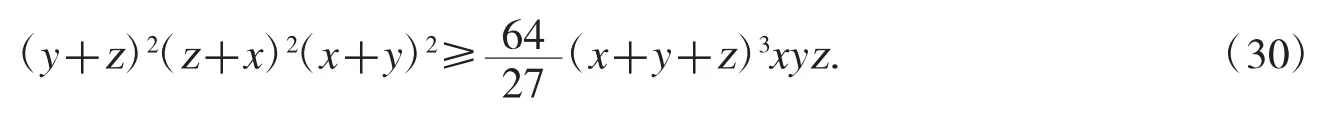
证明用诱导解法命令ydjf 可发现不等式(30)的如下隔离式

(a)式等价于

(b)式等价于
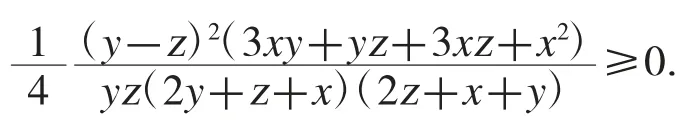
故不等式(30)获证.应该说这里对不等式(30)的证明是相当巧妙的.
例10在ΔABC 中,证明不等式
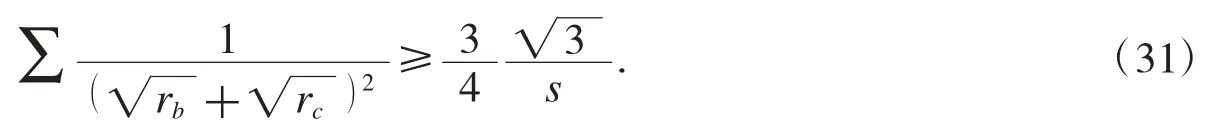
其中 ra,rb,rc是 ΔABC 的旁切圆半径.
证明不等式(31)代数化后为

作置换 x→x2,y→y2,z→z2,得

由柯西不等式,得

故要证(32)式,只需证

但由诱导解法命令ydjf 可发现不等式(33)的如下隔离式
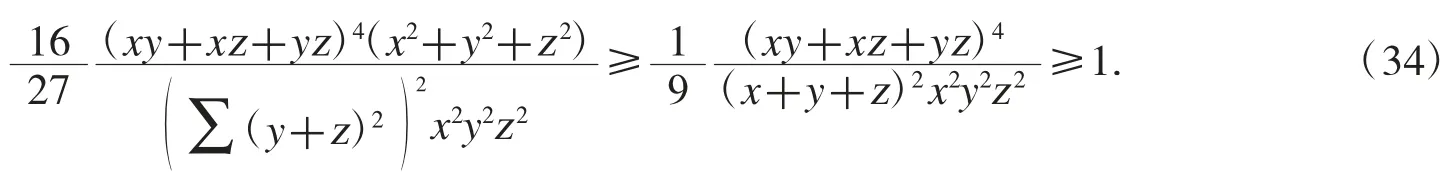
其中(34)式左边等价于 y2-xy+x2-yz-xz+z2≥0;(34)式的右边等价于

故不等式(32)成立,由此证得不等式(31).
5 结语
根式型不等式一直是不等式研究的热点和难点,而由本文的算法可知,根式型不等式最终可归结为多项式不等式的证明.自差分代换方法引入到机器证明以来,多项式不等式证明取得了很大进展,正像文献[5]指出的那样,“差分代换平凡规律的发现,可以说这是近期代数不等式研究最重要的成果之一”.另外配平方和,schur 分拆[12]等方法也极大地促进了多项式不等式的研究.也正因为如此,任何与有理化方法有关的研究结果格外受到关注.本文通过程序辅助寻找附加表达式的方式,利用赫尔德不等式和柯西不等式间接地实现了根式型不等式的有理化,从而对根式型不等式的证明有所突破.从上面的大量例子也可以看出,本文所解决的问题多数是多年遗留的难题.事实上,自本文中的算法出现之后,已经解决了数以百计的不等式难题.
最后再提两个问题:
1.对于有些根式不等式,我们一时还找不到附加表达式,使本文中的算法有效.例如网友dragonheart6 针对笔者的程序提供了陈计的如下不等式:设a,b,c>0,则

对于这类不等式,到底是附加表达式不存在呢,还是暂时找不到它,这个问题其实是有很深的理论意义的.
2.本文是通过试探验证的方法确定附加表达式的,因而效率不高,且算法被动消极有盲目性.能否像本文注5 所说的那样,通过预先设出附加表达式的形式,然后用赫尔德不等式和柯西不等式写出含有待定参数的需证式,对这个需证式的半正定性进行研究,从而得到参数值?这的确是一个值得重视的进一步研究思路.

