中心孔药型罩射流成型理论及仿真

韩 峰，张东辉，陈 放

(北京理工大学 爆炸科学与技术重点实验室，北京 100081)

中心孔药型罩是根据逆序起爆串联聚能战斗部的作用原理提出的特殊药型罩结构[1]，这种药型罩在轴线处开有一个通孔，用以保证后级射流通过。A.V.Malygin等[2]通过试验研究了飞片冲击起爆下中心孔聚能装药的侵彻能力；高靖[3-4]、王超等[5]对带孔椭圆药型罩聚能装药进行了数值模拟，研究了不同结构参数及起爆方式对射流成型的影响；李喜锋等[6]研究了中心圆柱高度对射流侵彻能力的影响；贾子健等[7]对带孔复合药型罩聚能装药的成型与侵彻钢靶过程进行了数值模拟研究；关荣[8]、张斐[9]等对带附加装置的中心孔药型罩的射流成型过程进行了数值模拟，研究了附加装置对射流成型的影响。上述学者的研究缺乏对中心孔药型罩射流成型的理论分析，同时关于罩顶药高及中心护管材料对中心孔药型罩射流成型的影响的相关研究也存在不足。

本研究在参考文献[10]的基础上，建立带中心孔药型罩压垮速度的计算公式，并利用AUTODYN-2D软件对不同结构的中心孔药型罩成型过程进行数值模拟，得出中心孔径、罩顶药高及中心护管材料等因素对射流头部速度的影响规律。本文研究结果可以为带中心孔成型装药提供设计依据。

1 中心孔药型罩射流成型理论计算模型

基本假设为：

1) 爆轰波到达罩面后，该罩微元立即达到压垮速度，并以不变的大小和方向运动；

2) 任意一个药型罩微元的压垮速度仅与装药及罩微元质量有关，内外罩壁不存在速度差；

3) 罩微元在爆轰产物驱动下向对称轴汇聚，运动过程中忽略微元间的相互作用，形成的射流仅沿轴向平动。

由PER理论可知，当中心孔聚能装药结构确定之后，射流头部速度只与药型罩的压垮角β、变形角δ以及压垮速度V0有关，但这3个参数无法直接通过PER理论得到。其中变形角δ和压垮角β可以用只含压垮速度V0作为变量的表达式表示，因此在计算射流头部速度时只需要补充药型罩的压垮速度V0的计算公式。

根据中心孔聚能装药的结构特点，建立中心孔药型罩压垮速度V0理论计算的模型如图1所示。图1中Cr和Cz分别表示罩微元对应的径向和轴向装药量；mi和mt分别指罩微元质量和对应的壳体质量；s和e分别表示罩顶药高和药型罩壁厚；R、Ri、Re分别为中心孔半径，罩微元到对称轴距离以及装药半径。

图1 药型罩压垮速度计算模型示意图

将药型罩的压垮速度V0分为径向速度Vr和轴向速度Vz两部分进行计算，其中径向速度Vr用管柱压垮公式[10]进行计算：

(1)

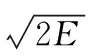
药型罩压垮的轴向速度通过平板压垮公式[10]计算，不过由于中心护管的存在，药型罩顶的装药并非全部作用在药型罩上，还有一部分装药消耗于中心护管的压垮过程上，因此在计算轴向速度时，作用在罩微元上的轴向装药量并非Cz，需要对其进行修正，修正后的药量用Cc表示。修正后的轴向速度计算公式如下：

(2)

Cc=ρ0·(V1+C·V2)

(3)

式中:ρ0为炸药初始密度;V1和V2分别为罩微元对应的轴向装药在罩壁范围内的体积和罩顶部分的体积;C为罩顶装药体积修正系数，由中心护管厚度决定。

对中心孔径为0.25Dk的药型罩形成的射流的头部速度进行计算，得出的计算值为8 216 m/s，通过数值仿真得出的结果为8 075 m/s，两者相差2%，证明理论计算结果与数值仿真吻合程度较好。本研究所提出的理论模型在一定程度上可以用于中心孔药型罩射流头部速度的工程计算。

2 中心孔药型罩射流成型数值模拟

2.1 中心孔聚能装药结构有限元模型

中心孔聚能装药结构主要有以下几部分组成：中心孔药型罩、中心护管、装药及壳体。药型罩材料为铜，中心护管材料根据研究内容的不同而改变，装药为8701炸药，壳体材料为铝。装药直径Dk=56 mm，装药长度L根据研究内容不同而改变；药型罩为带中心孔的等壁厚单锥型，厚度δ1=1.36 mm，锥角2α=50°；壳体厚度δ2=2 mm，起爆方式为装药顶部环起爆。

中心孔药型罩射流成型的数值模拟通过AUTODYN-2D软件实现。中心孔聚能装药为轴对称结构，且在射流成型过程中药型罩及装药都将发生大变形，故采用Euler算法并建立1/2模型进行求解，这样在保证计算精度的同时可以提高计算效率。在装药结构周围的Euler域填充空气，并将其边界定义为流出边界(Flow-out)，以消除爆轰波在边界处反射对射流成型的影响。在数值仿真的1/2模型中，环起爆通过设置一个偏心起爆点实现。建立的有限元模型如图2所示。

在图2所示的有限元模型中，药型罩和中心护管采用CU-OFHC材料，使用Shock状态方程及Steinberg Guinan本构模型；装药采用8701炸药，使用JWL状态方程，壳体材料采用AL7039，使用Shock状态方程及Johnson Cook本构模型。其中金属材料参数取自于AUTODYN-2D软件的材料库，8701炸药参数取自文献[11]，部分材料参数如表1～表3所示。

图2 射流成型有限元模型示意图

表1 CU-OFHC材料参数

参数名密度/(g·cm-3)Gruneisen系数C1/(m·s-1)参数值8.932.023 940参数名S1剪切模量/GPa屈服强度/MPa参数值1.48947.7120

表2 AL7039材料参数

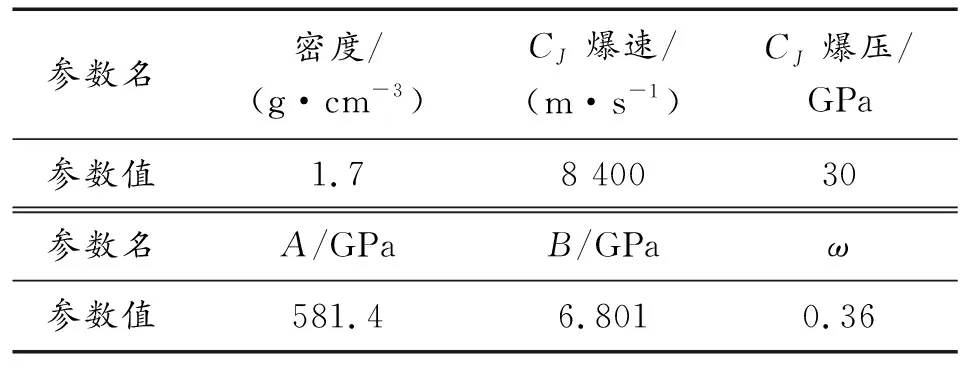
表3 8701材料参数

2.2 射流成型过程模拟

对中心孔径为0.25Dk，中心护管材料为铜，装药长度L=56 mm的中心孔药型罩射流成型过程进行数值模拟，中心孔药型罩在射流过程中的形成过程如图3所示。

由图3可以看出，装药起爆后，中心护管首先在爆轰波作用下压垮，t=6 μs时护管在轴线处完全闭合，护管尾部在爆轰产物的推动下形成类似于药型罩的反向空心结构；t=10 μs时护管尾部形成速度方向与射流头部相反的“反向射流”，“反向射流”头部以6 050 m·s-1的速度向后运动，同时射流头部以9 280 m·s-1的速度向前运动，整个侵彻体同时朝前后两个方向拉长；t=15 μs时侵彻体中部发生颈缩，出现独特的“双杵体”现象，同时“反向射流”头部出现断裂；t=20 μs时射流最前端断裂成数小段，剩余的射流头部速度达到8 624 m·s-1，且射流头部仍具有较大的速度梯度；t=30 μs时射流头部到达3倍炸高位置，射流拉伸得非常细长，此时射流头部速度为8 075 m·s-1，侵彻体尾部的“反向射流”剩余部分最大速度不足射流头部速度的10%。

图3 射流形成过程示意图

3 结构参数对射流成型的影响

3.1 药型罩中心孔径对射流的影响

定义药型罩中心孔径与装药直径的比值为λ。分别对装药长度L=56 mm，中心护管材料为铜，λ=[0，0.1，0.2，0.3，0.35，0.4，0.5]条件下的射流成型过程进行数值模拟，并分析λ对射流参数的影响。t=30 μs时不同λ值对应的射流头部速度与长度列于表4。

表4 不同中心孔径对应的射流参数

由表4可以看出，t=30 μs时，中心带孔的药型罩形成的射流头部速度与长度较无孔药型罩的射流而言均有所提高。而当λ≤0.35时射流头部速度及长度随着中心孔径增大而提高；λ=0.35时射流头部速度及长度达到最大，与无孔药型罩形成的射流相比，头部速度提高约23%，长度增大约28%；λ≥0.35时射流头部速度及长度随着中心孔径增大而降低。

3.2 罩顶药高对射流的影响

定义罩顶药高与装药直径的比值为μ。分别对中心护管材料为铜，μ=[0，0.15，0.25，0.3，0.5]条件下的射流成型过程进行数值模拟，并分析μ值对射流参数的影响。t=30 μs时不同μ值对应的射流头部速度与长度如图4所示。

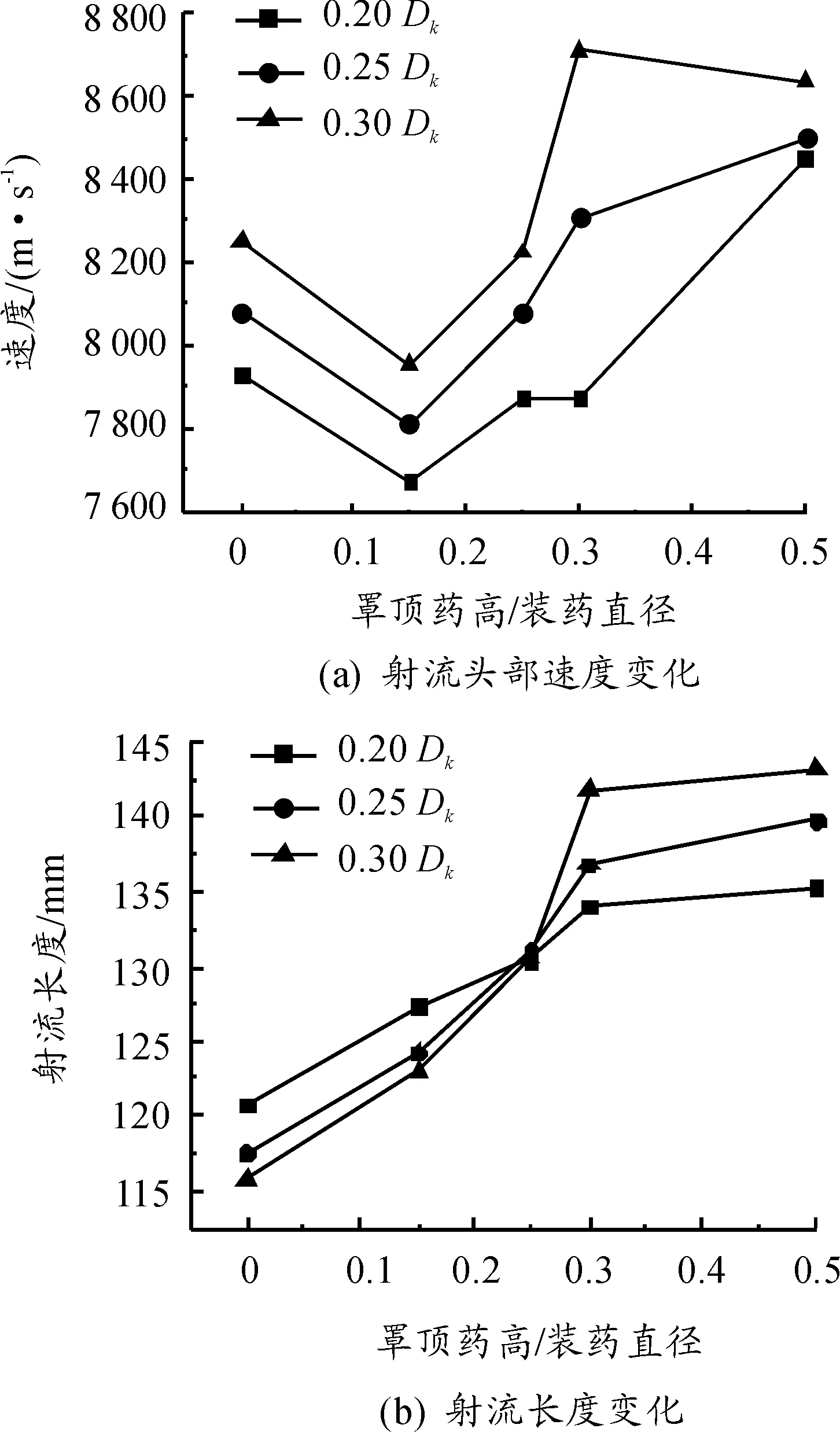
图4 罩顶药高对射流的影响

由图4(a)可以看出，对于3种不同孔径的药型罩，当罩顶药高大于零时，射流头部速度均随着罩顶药高的增加而增大，但当罩顶药高小于0.25Dk时的射流头部速度反而小于罩顶药高为零时的射流头部速度。通过分析可知，罩顶药高对射流头部速度的影响主要与作用在药型罩上的轴向装药量有关，罩顶药高增大使得作用在罩微元上的轴向装药量增加，提高了罩微元的压垮速度，从而使得射流头部速度增加。而当罩顶药高小于0.25Dk时，增加罩顶药高带来的轴向装药量的增益程度较小，此时从作用在药型罩壁上的爆轰波形(见图5)可以看出：罩顶药高为零时，爆轰波阵面与罩壁间的夹角更小，因而其射流头部速度更高；但随着罩顶药高增大到一定程度之后，增加轴向装药量给射流头部速度带来的增益效果超过了爆轰波阵面与药型罩壁面之间的夹角对射流头部速度的影响，所以之后的射流头部速度会超过罩顶药高为零时的射流头部速度。

由图4(b)可以看出，整体趋势上，3种不同孔径的药型罩形成的射流长度都随罩顶药高的增大而增长，但不同孔径下的射流长度的增长率却不同。出现这种现象的原因推断如下：当罩顶药高小于0.25Dk时，影响射流长度的主要因素是爆轰波入射角度的大小，中心孔径更小的装药结构的爆轰波入射角度更小，射流拉伸得程度更大，所以射流长度更长；而当罩顶药高超过0.25Dk之后，影响射流长度的主要因素变为罩微元闭合前运动距离的长短，中心孔径更大的药型罩的罩微元运动距离更长，因而形成的射流长度更长。

图5 不同罩顶药高下的爆轰波形

3.3 中心护管材料对射流的影响

分别对中心护管材料为尼龙、铝、钛、铜和钢的装药结构的射流成型过程进行数值模拟，并分析中心护管材料对射流参数的影响。t=30μs时不同中心护管材料对应的射流头部速度与长度如图6所示。

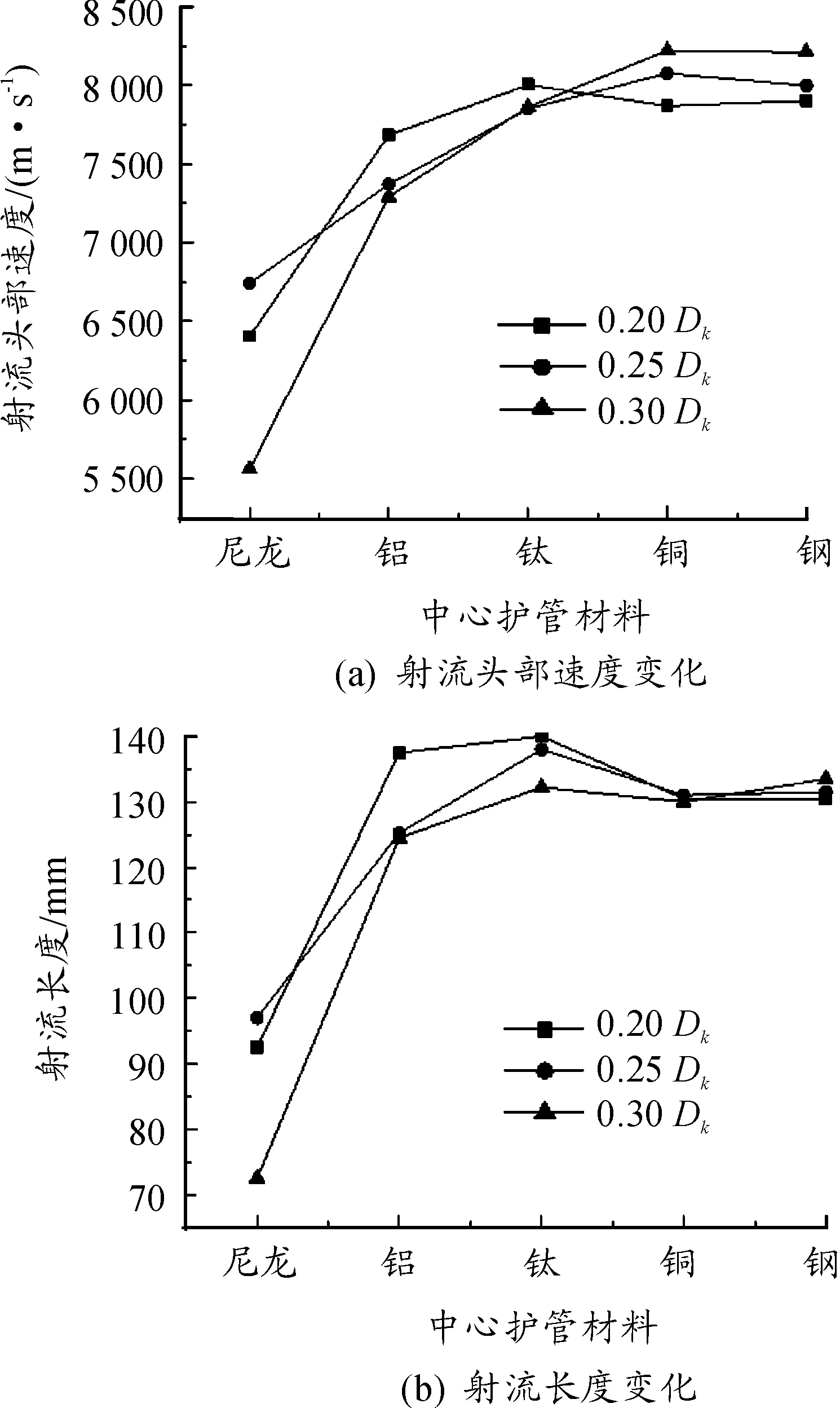
图6 中心护管材料对射流的影响

由图6(a)可以看出，总得来说，对于3种中心孔径的药型罩，射流头部速度都是随护管材料密度的增大而提高。但护管材料为钛时，药型罩中心孔径为0.2Dk时的射流头部速度反而更高，这是由于钛的密度比铜小，因而护管形成的射流速度比铜射流更大，这一部分钛射流出现对铜射流包覆的现象，两者形成一个连续的侵彻体，此时统计的射流头部速度其实是速度更高的钛射流头部的速度，故这种条件下的射流头部速度反而更高。

由图6(b)可以看出，射流长度总体上也是随着护管材料密度的增大而增长。但护管材料为铝和钛时的射流长度反而更长，出现这种现象的原因也是密度小的护管部分形成的射流会包覆在铜射流头部成为一个连续的侵彻体，此时统计的射流长度实际上是整个侵彻体的长度而非单纯的铜射流长度，故这种条件下的射流长度反而更长。

4 结论

1) 建立了中心孔药型罩射流头部速度计算的理论模型，并使用改进的PER理论对孔径为0.25Dk的药型罩形成的射流头部速度进行计算，计算结果与仿真结果较为吻合。

2) 孔径对中心孔药型罩射流的头部速度与长度有较大影响，存在最佳孔径0.35Dk，此时形成的射流头部速度与长度最大。

3) 罩顶药高会对中心孔药型罩射流的头部速度和长度产生影响。增大罩顶药高可以增加射流的头部速度和长度，但增益程度不如改变中心孔径的效果明显。

4) 射流头部速度及长度会随着中心护管材料密度的增大而增大；当护管材料密度较小时，中心护管形成的射流会对药型罩形成的铜射流产生包覆作用。