基于蚁群算法的测试用例优先排序*

张卫祥，齐玉华，魏 波，张 敏，窦朝晖

(北京跟踪与通信技术研究所，北京100094)

1 引言

随着信息技术的迅速发展，软件项目类型出现了很大变化，全新开发项目的比例不断下降，增强型软件项目所占比例不断增加。国际软件基准标准组ISBSG(International Software Benchmarking Stardards Group)发布的一项数据表明[1]，从1997年到2009年ISBSG搜集的5 000多个项目中，全新开发项目占比39%，而增强型项目占比59%。

增强型软件指的是，在原有软件功能、性能、接口等基础上，经过改造、优化和维护等技术手段，使其更好地适应新的使用目的或应用场景的软件。由于业务增长不断促进软件演化，软件产生速度远大于消退速度，软件迭代开发模式大行其道等原因，增强型软件项目近年来蓬勃兴起，在航天等诸多领域已占据主导地位。增强型软件的“增强”主要体现在3个方面：缺陷修复、功能扩充和软件优化。在增强型项目的软件测试中，不仅要验证和确认更动部分软件质量，还要保证软件原有的功能、性能和接口等没有因为更动而受到影响，测试难度大于新研软件。

对原有测试用例集进行有效维护(包括扩充、缩减和排序、优化等)是增强型软件测试的重要工作内容。一种最简单的维护策略是保持其不变，即重新执行已有的所有测试用例，但是往往存在项目预算或工程进度不允许、部分测试用例已失效、已有测试用例不能覆盖新增测试需求等诸多问题。为此，人们提出了一系列测试用例维护技术，包括测试用例集扩充、测试用例集缩减、测试用例选择、失效测试用例的识别和修复以及测试用例优先排序技术等[2]。

测试用例优先排序技术TCP(Test Case Prioritization)按照预先选定的测试目标，在特定排序准则指导下对测试用例重新排序，通过优化测试用例的执行次序来提高测试效率，是软件测试领域的一个研究热点[3]。在大规模软件的测试中，测试用例完全运行常常需要几周甚至几个月的时间，在这种情况下，测试人员希望对测试用例进行排序，使得优先级高的用例能够尽早地被执行，TCP技术应运而生。Wong等[4]较早进行了相关研究，结合测试用例历史覆盖信息和代码修改信息识别出冗余测试用例，并对非冗余测试用例根据其对代码的覆盖能力进行排序。Elbaum等[5]在2000年给出了TCP问题的一般性描述。Rothermel等[6]通过一系列有针对性的实验研究，证实了优先级技术在提高检错率方面的有效性。Tonella等[7]提出了一种机器学习的方法，利用测试者的经验对测试用例重要程度进行评估和排序。Shi等[8]引入Pareto效率方法，结合多目标优化来设置测试用例优先级。陈翔等[3]把TCP技术分为基于代码的、基于模型的和基于需求的TCP等3类，目前基于代码的TCP技术研究较为充分，基于需求的TCP技术的研究成果还不多见。

蚁群算法ACA(Ant Colony Algorithm)由Dorigo等[9]提出，是一种模拟蚂蚁群体觅食行为方式的仿生优化算法。ACA引入正反馈并行机制，具有较强的鲁棒性、优良的分布式计算机制、易于与其他方法结合等优点[10]，目前已成功解决了许多领域的复杂优化问题，成为智能优化领域的一个研究热点。Dorigo等[11]在基本蚁群算法的基础上提出了蚁群系统ACS(Ant Colony System)，让信息量最大的路径以较大的概率被选中，能够充分利用学习机制强化最优信息的反馈。Stützle等[12]提出了最大-最小蚂蚁系统MMAS(MAX-MIN Ant System)，将各个路径上的信息量限制在一个区间内变化，以避免算法过早收敛于非全局最优解。蚁群算法首先被应用于著名的旅行商问题，随后被广泛应用于网络路由、任务调度、系统辨识、图像处理等诸多领域[13 - 16]。

由于TCP问题本质上是寻找最优测试用例排列次序的离散优化问题，因此可利用ACA进行求解。顾聪慧等[17]基于蚁群算法提出了一种多目标优化方法，针对平均语句覆盖率和有效执行时间2个优化目标，实现了测试用例集的优化排序并改进了多目标解集优劣评价方法。邢行等[18]提出一种基于上位基因段的信息素更新策略，以改进蚁群算法在求解多目标测试用例优先排序时收敛速度缓慢、易陷入局部最优的问题。

本文的主要贡献在于：

(1)提出了一种基于ACA求解面向需求的TCP问题的方法TCP-ACA(ACA for TCP)，并给出了2种不同的实现方式，可直接应用于黑盒测试。

(2)提出了测试用例吸引度的概念，并基于其定义了测试用例之间的距离，作为外启发信息引导蚁群的寻优。

(3)提出了基于需求的一般性评价指标，能够对测试用例序列的优劣进行量化比较。

(4)改进信息素更新策略，引入局部最优解突变策略，提高了全局最优解收敛速度和搜索能力。

2 问题的提出

2.1 基于需求的测试优先排序

TCP问题的一般性描述为[5]：给定测试用例集T、T的全排列集PT、排序目标函数f:PT→R，寻找T′∈PT，使得对∀T″∈PT(T″≠T′)，有f(T′)≥f(T″)。由问题描述可知，目标函数f的输入是测试用例执行次序，输出为1个数值，数值越大则排序效果越好。

按照排序依据的不同，TCP技术可分为基于代码的、基于模型的和基于需求的TCP技术等3类[3]。目前的研究主要集中在基于代码的TCP技术，从贪婪法、机器学习法、融合专家知识法等不同角度已有不少的研究成果。

基于需求的TCP技术的研究成果还比较少。屈波等[19]基于测试用例的设计信息，提出了1组基于需求的测试用例优先级动态调整算法。Zhang等[20]提出了考虑测试需求优先级和测试用例执行开销的基于Total策略和Additional策略的TCP技术。Krishnamoorthi等[21]基于软件需求规约，在对测试用例进行排序时考虑了包括客户定义的需求优先级、需求变动信息、需求实现复杂度、需求完整性、需求可追踪性和缺陷影响程度等更多的影响因素。

张卫祥等[22]指出，影响基于需求的TCP技术的各种因素，总体上可分为测试成本型因素(Cost-Keys)和测试收益型因素(Win-Keys)2大类，有的因素所起的作用和测试用例次序是正相关的，有的是负相关的，有的影响大，有的影响小，但都可以通过加权的方式进行归一化。

不失一般性，令Cost-Keys因素全集为C={c1,c2,…,cn}，Win-Keys因素全集为W={w1,w2,…,wm}，对任一测试用例ci∈T，有：

Wi=h(W),Ci=g(C)

(1)

其中，Wi称为测试用例ci的综合收益，表示全部测试收益型因素对测试用例ci的综合影响；Ci称为测试用例ci的综合成本，表示全部测试成本型因素对测试用例ci的综合影响；h:W→R,g:C→R分别为测试收益型因素、测试成本型因素的权值函数。请注意，这里我们对文献[22]中的Wi和Ci进行了扩展，因为这里的h,g不仅可以是线性函数，还可以是非线性函数。

2.2 测试用例序列评价指标

为衡量TCP技术的有效性，需要对排序结果进行评价。与随机顺序测试相比，TCP的优势是能够更快地检查出错误。基于此，Elbaum等[5]采用测试用例使用个数和检测错误个数之间的关系来量化测试用例序列的优劣，给出APFD(Average Percentage of Fault Detection)评价指标。由于无法在测试用例全部执行前知道测试用例的缺陷检测信息，APFD存在着明显不足。Li等[23]随后提出APBC(Average Percentage of Block Coverage)、APDC(Average Percentage of Decision Coverage)和APSC(Average Percentage of Statement Coverage)等系列指标，分别以测试用例序列对程序块、分支和语句的覆盖速率为考核对象，显然这些指标更适合于基于代码的结构测试。

在基于需求的功能测试中，测试人员以软件规格说明为依据。一般地，先将软件需求转化为测试需求，然后把测试需求细化分解为测试点，最后针对测试点进行测试用例设计，形成测试用例集合。为此，张卫祥等[24]提出基于测试点覆盖的评价指标APTC(Average Percentage of Test-point Cove-rage)。对于测试用例集Φ={T1,T2,…,Tm}，APTC的计算公式定义为[24]：

(2)

其中，m为测试用例个数，n为测试点个数，TTi表示首个可覆盖到第i个测试点的测试用例在该用例序列中所处的次序。APTC的取值在0～1，取值越大表示对测试点覆盖的速度越快。

类似于文献[22]，调整评价目标为单位综合成本取得的综合收益，利用公式中的综合收益和综合成本对APTC进行改造，提出测试平均收益率评价指标eAPWC(enhanced Average Percentage of Win-cost Coverage)。eAPWC在形式上与APWC[22]一致，公式化表示为：

(3)

其中，各个变量的含义与式(1)和式(2)中的相应变量一致。当所有测试用例的综合收益相同且综合成本相等时，式(3)就是式(2)，即APTC指标为eAPWC指标的一种特殊情况。

3 基于蚁群算法的求解方法

本节给出基于蚁群算法求解TCP问题的方法TCP-ACA。首先介绍基本蚁群算法，随后给出TCP-ACA的设计实现及基本流程。

3.1 基本蚁群算法

基本蚁群算法是采用人工蚂蚁的行走路线来表示待求解问题可行解的一种方法。每只蚂蚁在解空间中独立地搜索可行解，当碰到一个还没有走过的路口时，就随机挑选一条路径前进，同时释放出与路径长度相关的信息素。路径越短，信息素的浓度就越大。当后续的蚂蚁再次来到这个路口时，会以相对较大的概率选择信息素较多的路径，并在行走路线上留下更多的信息素，影响后来的蚂蚁，从而形成正反馈机制。随着算法的推进，代表最优解路径上的信息素逐渐增多，选择它的蚂蚁也逐渐增多，而其它路径上的信息素却随着时间流逝而逐渐消减，最终整个蚁群在正反馈的作用下集中到代表最优解的路径上，也就找到了最优解[25]。

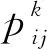
(4)

为了避免残留信息过多而淹没启发信息，在每只蚂蚁走完1步或者完成对所有城市的遍历后，要对信息素τij(t)进行更新：

τij(t+1)=(1-ρ)τij(t)+Δτij(t)

(5)

(6)

其中，Lk为蚂蚁k遍历城市的路径长度和；Q为1个常量。

对于求解TCP问题，蚁群算法具有天然的适应性，但同时也存在对参数敏感、易于陷入局部最优等不足，需要对基本蚁群算法加以改造。

3.2 基于需求的测试用例距离

针对基于需求的测试优先排序问题，给出基于测试点的测试用例距离定义。首先引入测试用例的吸引度概念。

定义1(测试用例吸引度) 对于任意2个测试用例ci和cj，假设它们所覆盖的测试点集合分别为TPi和TPj，定义ci与cj的吸引度为aspirationij：

aspirationij=λ×(∑p∈TPi∪TPjvp-μ×

∑q∈TPi∩TPjvq)/(Ci+Cj)

(7)

其中,vp和vq表示测试点p和q的价值(重要程度)；Ci和Cj分别表示测试用例ci和cj的综合成本(如式(1)定义)；λ,μ为调节因子。

根据定义可知，2个用例间的吸引度与它们共同覆盖的测试点的总价值正相关，与测试用例的综合成本负相关，特别地，2个用例所覆盖测试点的相似程度越高，其吸引度反而越低。

定义2(测试用例距离) 对于任意2个测试用例ci和cj，定义它们之间的距离dij为(其中ε为1个小常数，比如10-3)：

(8)

可以看出，2个测试用例覆盖的测试点越多、价值越高且相似程度越低，其距离越小；反之，距离就越大。这与TCP问题的求解目标是一致的。

3.3 TCP-ACA设计与实现

根据对测试用例间距离及测试用例序列的评价方式的不同，TCP-ACA有2种实现方式：

方式1(TCP-ACA-1)：定义用例间的距离(利用式(8))，令测试用例序列的长度为其路径上各用例间距离之和，按照类似于TSP问题求解的思路，以路径长度短者优为原则评价测试用例序列的优劣，并进行迭代更新。

方式2(TCP-ACA-2)：不定义用例间的距离(或者令各用例间距离相等)，在蚁群随机搜索生成路径后，以式(3)为指标评价测试用例序列的优劣，给局部最优解对应路径增加额外信息素，并进行迭代更新。

无论哪一种方式，为了保证对TCP问题的适用性及提高对全局最优解的搜索能力，TCP-ACA改进了基本蚁群算法的解构建策略、解评价策略和信息素更新策略，并引入了局部最优跳出策略。

3.3.1 解的构建

对于蚁群中的每只蚂蚁，单独构建解。与TSP不同的是，测试用例序列的首尾不相连。

求解时，蚂蚁首先随机选择1个测试用例作为初始点，然后从初始点开始，根据转移概率逐个访问下1个未被访问过的测试用例，直至所有的测试用例被访问1遍，得到1个测试用例遍历序列，即完成解的构建。

转移概率依据式(4)计算得到。对于蚂蚁k、测试用例ci和测试用例cj，可采用最大最小蚂蚁系统MMAS[12]的策略。τij(t)表示测试用例ci和测试用例cj间路径的信息素浓度，在每只蚂蚁完成1次遍历后进行更新，更新策略将在3.3.4节介绍；每条路径上的信息素量被限制在[τmax,τmin]内，并在初始时设定为区间上限，[τmax,τmin]由式(9)和式(10)计算得到:

(9)

(10)

其中,L(sgb)表示全局最优解路径的长度(在第1次迭代完成前设置为1个经验值)，σ为精英蚂蚁的数量(产生第1代前为0)。

式(4)中的ηij(t)是外启发式信息，对于TCP-ACA-1，ηij(t)=1/dij，dij由式(8)定义；对于TCP-ACA-2，ηij(t)=const，const为1个常数(比如1)。

计算得到转移概率后，按照轮盘赌策略[25]选择下1个测试用例。待所有蚂蚁都完成1次遍历后，就得到了1组解的集合，集合中解的个数与蚂蚁数量相等。

3.3.2 解的评价

对于解集合中的每个解，需要评价其优劣。TCP-ACA的 2种实现方式的评价策略不同。

对于TCP-ACA-1，首先计算解的长度，解的长度为测试用例序列路径上各用例间距离之和；然后，以长度小者优为原则进行解的评价，最小者为最优解。

对于TCP-ACA-2，首先计算解的适应度，解的适应度以执行测试用例序列时单位综合成本取得的综合收益为评价目标，利用式(3)所定义的eAPWC指标得到；然后，以适应度大者优为原则进行解的评价，最大者为最优解。需注意的是，eAPWC为一般性指标，可通过设置限定条件或选择特定参数使其简化，例如，假设所有测试用例的综合收益相同且综合成本相等，eAPWC就等价于文献[24]中的APTC。

3.3.3 最优解集的更新

最优解集的作用是收集在整个搜索过程中产生的当前全局最优解，在每1次迭代完成时更新1次。

在最大最小蚂蚁系统MMAS中，找到以下2种最优路径之一的蚂蚁,允许其释放信息素(其它蚂蚁不允许)：本次迭代中的最优路径，或者当前已发生的所有迭代中的最优路径。

在每1次迭代完成后，首先要对每个解的优劣进行评价，标记本次迭代中的最优路径；然后将本次迭代中的最优路径与最优解集中的最优路径进行比较，更新最优解集。

3.3.4 信息素的更新

更新信息素的目的是为了增加较优路径上信息素的浓度，减小较差路径上的信息素浓度，从而引导蚂蚁向着更好的方向搜索。TCP-ACA的2种实现方式的信息素更新策略不同。

对于TCP-ACA-1，采用信息素2次更新策略：先使用MMAS的信息素更新策略进行首次更新，然后再对全局最优路径上的部分长距离子路径进行2次更新。具体地：

(1)首次更新。使用MMAS的信息素更新策略对式(5)进行改造，有：

(10)

(2)2次更新。考虑到某些最优路径中的子路径由于距离较长使得被选择的概率较小，可能导致被错过而无法构成潜在全局最优解，在每次迭代后，增加对当前全局最优路径的子路径的路径贡献度[26]判断，并对路径贡献度大于给定阈值的进行2次更新。对于子路径(cj→ci)，定义其路径贡献度为dij/L(sgb)，对给定阈值q0，按式(12)计算信息素变化率：

(12)

对于TCP-ACA-2，只进行首次更新，不进行2次更新。

3.3.5 局部最优解的突变

蚁群算法的正反馈机制有利于算法快速收敛，但也能导致较优路径上的信息素越积越多，使得搜索陷入局部最优而停滞。为了提高算法跳出局部最优的能力，TCP-ACA引入变异策略，将趋于停滞的局部最优解替换为突变产生的新解。

TCP-ACA的2种实现方式的局部最优解突变策略相同。具体地，假设局部最优路径(即当前全局最优解)为c1→c2→…→ci→…→cj→…→cn，随机选择路径上的2个位置i和j，交换其上的测试用例ci和cj而产生突变，形成突变解；然后，评价突变解，如果它优于原有路径，则更新局部最优解，否则不更新。如此循环多次，可以增强路径的多样性，提高全局寻优能力。

3.4 TCP-ACA基本流程

TCP-ACA的基本步骤包括：

(1)初始化。分别设置最大迭代次数、信息素挥发系数、蚂蚁数量、测试用例数量以及当前迭代次数、禁忌表索引等变量。将蚂蚁随机放在各测试用例上，作为起始点。

(2)构建解空间。针对每只蚂蚁执行以下步骤：

①根据状态转移概率公式计算蚂蚁选择测试用例的概率；

②使得蚂蚁移动到具有最大转移概率的测试用例；

③重复①、②，直到蚂蚁遍历所有测试用例。

(3)评价解的优劣。逐一计算本次迭代生成的各个解的适应度值，得到本次最优解。

(4)执行局部最优解突变。如果最优解连续没有得到改善，则判定陷入局部最优，执行局部最优解突变；否则，直接执行(5)。

(5)更新最优解集。利用本次最优解更新最优解集。

(6)更新信息素浓度。根据信息素更新策略，对各个测试用例连接路径上的信息素进行首次更新和2次更新。

(7)判断是否终止。判断是否满足最大迭代次数等终止条件，如果满足，算法终止；否则，返回(2)。

4 实验验证

4.1 实验设置

实验采用三角形分类程序，并把实验结果与已有文献[22,24]的结果进行比较。三角形分类程序的主要功能是利用三角形各边的取值及相互关系来判断三角形类型，包括不等边三角形、等腰三角形、等边三角形以及非三角形等[24]。三角形分类程序共包含7个测试点、6个测试用例，其测试用例与测试点的对应关系如表1[24]所示。

蚁群算法、粒子群算法和遗传算法都属于启发式算法，不能保证在任何情况下都能得到最优解。为了检验算法的效果，本文从最优解的质量、最优解的成功率等2个方面进行比较分析。

为了便于比较，分别采用eAPWC的2种简化变体eAPWC-1和eAPWC-2作为TCP-ACA-2的评价指标，其中，eAPWC-1的简化原则是令所有测试用例的综合收益相同且综合成本相等，即如果所有测试用例的综合收益相同且综合成本相等，eAPWC就简化为eAPWC-1，等价于文献[24]中的APTC和文献[22]中的APWC-1；eAPWC-2的简化原则是假设每个测试点的重要程度及每个测试用例的成本不等，以单位测试成本覆盖测试点的重要性程度值作为评价目标，eAPWC-2等价于文献[24]中的APTC_C和文献[22]中的APWC-2。

Table 1 Correspondence between test points and test cases of the triangle classification program表1 三角形分类程序的测试点与测试用例的对应关系

参照段海滨[10]的蚁群算法参数设定方法，经多次实验调整，设定TCP-ACA的主要参数如下：

TCP-ACA-1：蚁群规模m=10，信息启发式因子α=1，期望启发式因子β=5，信息素挥发系数ρ=0.1，信息素强度Q=0.3，最大迭代次数为Nmax。

TCP-ACA-2：m=10，α=1，β=5，ρ=0.1，Q=1，Nmax。

4.2 结果分析

对TCP-ACA的2种实现方式TCP-ACA-1、TCP-ACA-2分别进行实验，而TCP-ACA-2又分别使用了eAPWC-1、eAPWC-2等2种评价指标。因此，共有3组实验(分别采用eAPWC-1、eAPWC-2、用例距离进行解评价)，每组实验重复进行15次。

TCP-ACA与TCP-DPSO[22]、GA[24]等不同方法求得的最优解如表2所示，最优解成功率如表3所示(其中的数值表示最优解次数/总次数)。TCP-DPSO[22]、GA[24]没有使用用例距离作为评价指标。

Table 2 Comparison of the optimal solution quality表2 最优解质量的比较

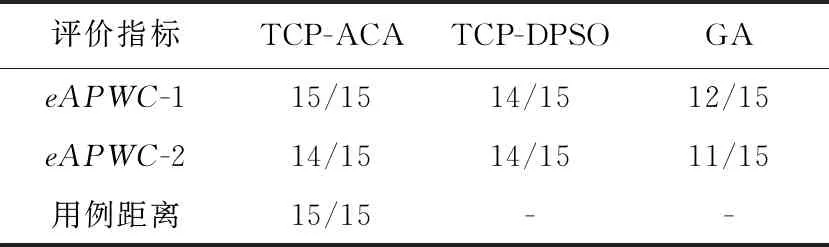
Table 3 Comparison of optimal solution success rates表3 最优解成功率的比较

作为比对，还采用了随机测试方法，同样进行15次实验，每次实验随机生成100个测试用例序列，得到的解的分布情况如表4所示，大体上呈正态分布，最优解的生成几率在2%～3%。

由表2和表3可以看出：从所求解的最优解的质量上，TCP-ACA大幅优于随机测试，与TCP-DPSO、遗传算法相当；从求解最优解的成功率上，TCP-ACA要好于遗传算法，且比TCP-DPSO略优。总体而言，TCP-ACA方法是可行的，具有很好的全局寻优能力，效果上优于粒子群算法、遗传算法和随机测试。

Table 4 Distribution of solutions by random testing表4 随机测试生成解的分布情况

再对TCP-ACA的不同实现方式TCP-ACA-1和TCP-ACA-2的演化过程进行进一步分析，其演化过程如图1所示。

Figure 1 Evolution of the average and optimal solution of TCP-ACA图1 TCP-ACA的最优解及平均解的演化

从图1可以看出：首先，从最优解的收敛效果来看，不论TCP-ACA-1，还是TCP-ACA-2(eAPWC-1)、TCP-ACA-2(eAPWC-2)，收敛效果都不错，对最优解的搜索速度都很快，尤其是TCP-ACA-1和TCP-ACA-2(eAPWC-1)，只需迭代几个轮次就能收敛。其次，从平均解的收敛效果来看，TCP-ACA-1最好，平均解的收敛趋势好，速度也比较快；TCP-ACA-2(eAPWC-1)次之，平均解也呈收敛趋势；TCP-ACA-2(eAPWC-2)最差，平均解的收敛趋势不明显。造成这种情况的原因在于：TCP-ACA-1以用例距离作为评价指标，用例距离能直接作用于任意2个用例之间，会对蚁群起到很好的正反馈作用；而TCP-ACA-2以eAPWC-1或eAPWC-2为评价指标，评价效果作用在整条路径上，路径上的各用例被同等激励，不能有效体现用例间差别，对蚁群的正反馈作用较弱；尤其是TCP-ACA-2(eAPWC-2)，由于指标eAPWC-2较eAPWC-1更复杂，导致其对用例的激励作用更加不直接、不明确，对蚁群的正反馈作用也最弱，不能有效引导蚁群整体向最优解集中。

5 结束语

测试用例优先排序问题在本质上是一个离散组合优化问题。本文利用蚁群算法的鲁棒性好、并行性强等特点，提出了基于蚁群算法的方法TCP-ACA，实现了对基于需求的测试用例优先排序问题的求解，能够直接应用于增强型软件测试和黑盒测试。

根据不同的解评价策略，本文用2种方式实现了所提出的TCP-ACA方法。TCP-ACA-1提出吸引度的概念并基于其定义测试用例间的距离，把路径上各用例间距离之和作为测试用例序列的长度，依据路径长度短者为优的原则评价测试用例序列的优劣，利用最优蚂蚁更新信息素并迭代寻优。TCP-ACA-2不定义用例间距离，在蚁群随机搜索生成路径后，分别以本文提出的eAPWC-1或eAPWC-2作为指标评价，依据指标大者为优的原则评价测试用例序列的优劣，给最优路径增加额外信息素并迭代寻优。实验结果表明，TCP-ACA方法具有很好的全局寻优能力，整体效果上优于粒子群算法、遗传算法和随机测试。

随着人工智能的蓬勃发展，智能化技术的应用日益广泛。把智能优化技术用于求解测试用例优先排序、测试用例和测试数据的自动生成等软件测试领域中的热门问题，是一个可行的技术方向，具有很好的研究价值。下一步，我们将就各种智能化技术在软件测试中的应用做进一步的研究。