一种基于多模数据的室内定位算法*
贾玉福,刘文平,胡胜红
(1.湖北经济学院信息管理与统计学院,湖北 武汉 430205;2.湖北经济学院信息工程学院,湖北 武汉 430205)
1 引言
机器人和移动手持终端的室内导航应用需求的增长,促使室内定位技术逐渐成为研究热点。当前对室内定位技术的研究主要是利用红外、蓝牙、超宽带UWB(Ultra Wide Band)、RFID和WiFi等短距离无线通信技术[1 - 4],采用三边定位法[5,6]或位置指纹法[7]来实现。由于信号多径效应的影响,测距误差使三边定位法很难保证定位精度与系统稳定性[8]。位置指纹法的定位精度主要依赖指纹数据库中的样本数据质量[9],但传统的基于RSSI的指纹数据往往受到诸多因素的影响,采样数据随时间和环境变化而动态变化,导致实时采样与指纹数据库中的样本数据出现明显失配[10]。为此,Xu等人[11]提出了利用计算机视觉信息辅助进行室内定位的算法,实践证明,利用计算机视觉技术进行图像空间结构信息交叉比对,可在室内定位实践中取得更好的结果[11 - 14]。受此启发,本文利用图像兴趣点的尺度不变特征SIFT(Scale-Invariant Feature Transform)[15 - 21]和WiFi场景信息进行室内定位。定位过程分为前期准备阶段和实时定位阶段。在前期准备阶段,首先利用坐标变换原理分析并建立图像平面坐标与世界坐标系坐标之间的数学关系,然后选定室内场景中的信标(即根据SIFT算法通过多角度测试比对出的稳定的图像兴趣点),计算信标的SIFT特征,根据室内建筑设计图获取信标的定位坐标信息。在实时定位阶段,首先通过SIFT算法进行信标识别,再利用上述数学关系求解观察点的位置与信标的距离,最后利用三边定位法实现物体定位。针对定位求解得到多个定位坐标的情况,本文利用堆栈自编码器SAE(Stacked Auto Encoder)与DNN相结合的深度学习网络结构,以多个自定义WiFi特征为输入数据,11个距离分类类别为标签,辅助判别观察点的真实定位信息。
2 测距理论模型
本文利用4个坐标系来分析三维场景中物体的坐标与其在图像中对应的平面坐标之间的数学关系。坐标系分别为图像像素坐标系OpUV、图像物理坐标系OXY、摄像机坐标系OcXcYcZc和世界坐标系OwXwYwZw。假定坐标系之间的关系如下:图像像素坐标系与图像物理坐标系处于同一平面,但图像像素坐标系的原点在图像的左上角(单位为像素),图像物理坐标系的坐标原点在图像的中心(单位为mm),如图1a所示。摄像机坐标系的XcYc平面与图像物理坐标系XY平面平行,原点位于镜头位置。世界坐标系的XwYw平面位于地面,如图1b中的ABCD平面。世界坐标系经过仿射变换可以转化为摄像机坐标系,摄像机坐标系经过投影变换可以变换到图像物理坐标系。

Figure 1 Camera projection model图1 摄像机投影模型
设摄像机焦距为f,水平视角和垂直视角分别为2α和2β,图像的宽与高分别为Wc和Hc,像素点坐标(u,v)与图像物理坐标中对应的点(x,y)之间的关系为:
(1)
点(x,y)与摄像机坐标系中对应点的坐标(xc,yc,zc)(注意:zc<0)之间的关系为:
(2)

(3)
反过来,摄像机坐标系中点(xc,yc,zc)与世界坐标系中点(xw,yw,zw)之间的关系为:
(4)
合并式(1)、式(2)、式(4),可得式(5):
(5)

(6)


(7)
3 定位算法
3.1 求解多个定位坐标
由图1b可知,摄像机在地面的垂直投影为点H(0,-l),则摄像机与信标(xw,yw,zw)的地面水平距离为:
(8)
将式(6)和式(7)代入式(8)中可知,影响距离d求解精度的因素有2个:摄像机的高度h和俯仰角γ。为比较二者对距离求解精度的影响,使用HUAWEI Mate 9手机在如下条件下进行采样:信标距离地面的高为1.4 m,手机距离地面1.5 m,手机与信标的水平距离为10 m。将采样结果与上述参数代入式(6)~式(8)中,改变手机的俯仰角,其他参数不变,得到的距离变化数据如表 1所示。固定俯仰角γ(=83.5°)不变 ,改变手机与地面的距离,其他参数不变,得到的距离变化数据如表2所示。对比表1和表2的数据可知,手机与地面的距离对距离求解的影响较小,而俯仰角则对距离求解起关键作用,而且在室内定位实践中不具备实时准确测量俯仰角γ的条件,但可以对h值有较好的估计。因此,本文提出的算法基于如下过程:假定h已知,引入图像中2个信标之间的平面距离作为约束条件求解未知参数俯仰角γ,再根据γ求出信标在世界坐标系中的坐标,最后根据手机到2个信标的平面距离实现定位。
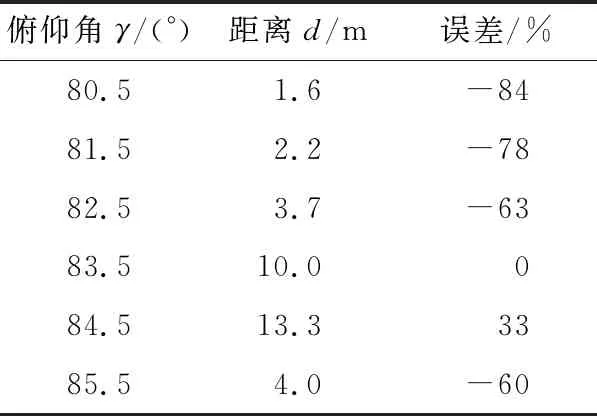
Table 1 Distance data varying with angle of pitch表1 随俯仰角变化的距离数据
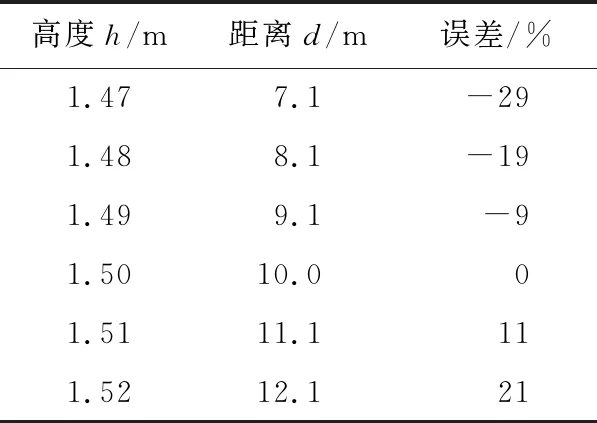
Table 2 Distance data varying with altitude表2 随高度变化的距离数据

3.2 利用SAE和DNN模型判别定位坐标
对于在3.1节求得的2n个定位坐标,本文利用WiFi信息和深度神经网络DNN来识别哪一个是观察点的真实定位坐标。其基本思想是:利用DNN分别计算在观察点处采集的WiFi信息与在2n个定位坐标处的WiFi信息的相似度,选取相似度最大时对应的定位坐标作为观察点的真实坐标。其具体过程分为训练阶段和预测阶段:在训练阶段,首先将定位场景划分为网格,在网格的交叉点处预先采集WiFi信息,然后将距离在10 m内的任意2个交叉点组成1对,并将成对的交叉点的实际距离通过四舍五入取整离散化为整数,再将每对交叉点的WiFi信息转化为1个特征矢量fv(特征矢量的产生方法见3.3节),把成对节点的特征矢量fv作为输入,离散化的距离作为分类标签ci,如图2所示,在1个具有3层SAE和2层DNN的网络上进行训练,分类器采用Softmax。在预测阶段,首先判断各个定位坐标是否在网格内,如果是,则用与定位坐标最近的网格交叉点的WiFi信息作为定位坐标的WiFi信息,否则将该点抛弃,然后分别将观察点处采集的WiFi信息与2n个定位坐标的WiFi信息转化为2n个特征矢量,以2n个特征矢量为输入,利用模型分别计算距离。最后选取距离最小时对应的定位坐标为观察点的定位坐标。
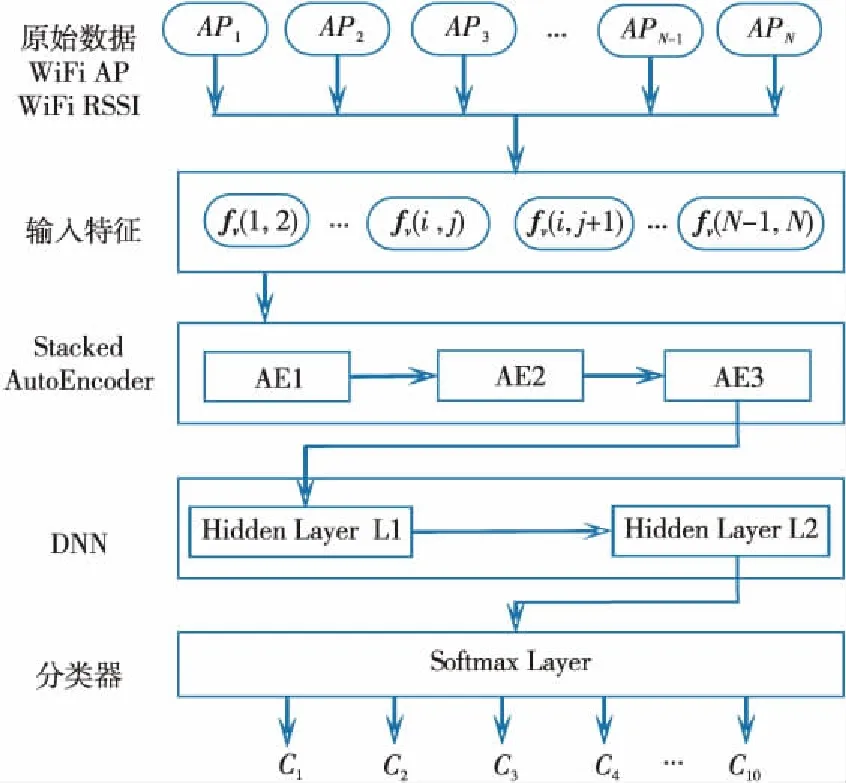
Figure 2 Distance estimation network learning model图2 距离估计的网络学习模型
3.3 特征矢量的设计
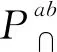
设APs为在网格内所有交叉点检测到的 WiFi AP(Mac地址)集合,APs的维度为ns=|APs|。对于位置a,设Lsa为在APs内Wifi AP对应的WiFi RSS的绝对值集合,即当APs(i)∈APa且APs(i)=APa(j)时,Lsa(i)=La(j),APs(i)∉APa时,Lsa(i)= 99(i≤ns,j≤|APa|)。求解Lsa中的每1个元素在Lsa中按升序排列产生的排名,记为Csa。同理,对于位置b,产生Csb。对于i≤ns,求解|Csa(i)-Csb(i)|共产生ns个特征。将此ns个特征与上述78个特征按同一顺序排列共同组成成对位置点a,b的特征矢量fv。
3.4 定位算法的计算过程
综上所述,本文提出的定位算法计算过程如下:
(1)通过手机拍照得到前方图像,利用信标识别算法识别出图像中的2个信标m1、m2,获取信标的图像坐标(u,v);
(2)根据信标m1和m2的定位坐标计算2个信标间的距离Distm1,m2;
(3)根据fm1,m2(γ)=0求解γ,得到γ的n个解;
(4)将n个γ分别代入式(7),计算信标m1和m2的yw,然后将yw代入式(6),计算信标m1和m2的xw;
(5)将xw和yw代入式(8)中计算观察点与信标m1和m2的平面距离;
(6)根据观察点与信标m1和m2的平面距离、m1和m2的定位坐标计算得到2n个定位坐标;
(7)将观察点分别与2n个定位坐标组成2n对位置点,利用WiFi信息转换得到的特征矢量,在SAE+DNN模型上计算得到2n个距离类别;
(8)选取最小距离类别对应的定位坐标为观察点的定位坐标。
4 实验分析
4.1 实验方案
为了测试算法的性能,我们在武汉大型购物商场凯德1818进行了大量的实验。如图3所示,根据室内地砖的边界线将环境划分为N×M的网格。收集1组位于不同网格交叉点的成对WiFi信息,并依据网格计算成对交叉点的距离组成数据集。在SAE和DNN模型的训练阶段,实验在CPU为Intel酷睿i7-4790,显卡为GTX1060的环境上运行,模型采用Tensorflow框架实现,以54K个节点对的WiFi特征矢量作为模型的输入,节点对的离散距离作为标签,在整个数据集上训练30代,训练时间约为25 h。在定位阶段,实验设备采用HUAWEI Mate 20X手机,系统为Android 9.0,图像分辨率为 2736×3648,摄像机水平视角为52.47,垂直视角为 66.37。为了充分分析摄像机高度、观察点与信标的距离、信标的高度等因素对定位精度的影响,本文设计了11套方案(如表3所示)进行实验。在不同的高度竖直固定手机,绕Xc轴旋转手机逐渐缩小俯仰角,每旋转1次便对前方含有信标的场景拍照采样。每套方案采样10次。每次定位计算的耗时为毫秒级。

Figure 3 Experimental environment图3 实验环境
4.2. 结果分析
方案1~5是在信标高度和摄像机高度等参数相同的条件下,观察摄像机与信标地面距离d的变化对定位误差的影响;方案6~8、方案9~11分
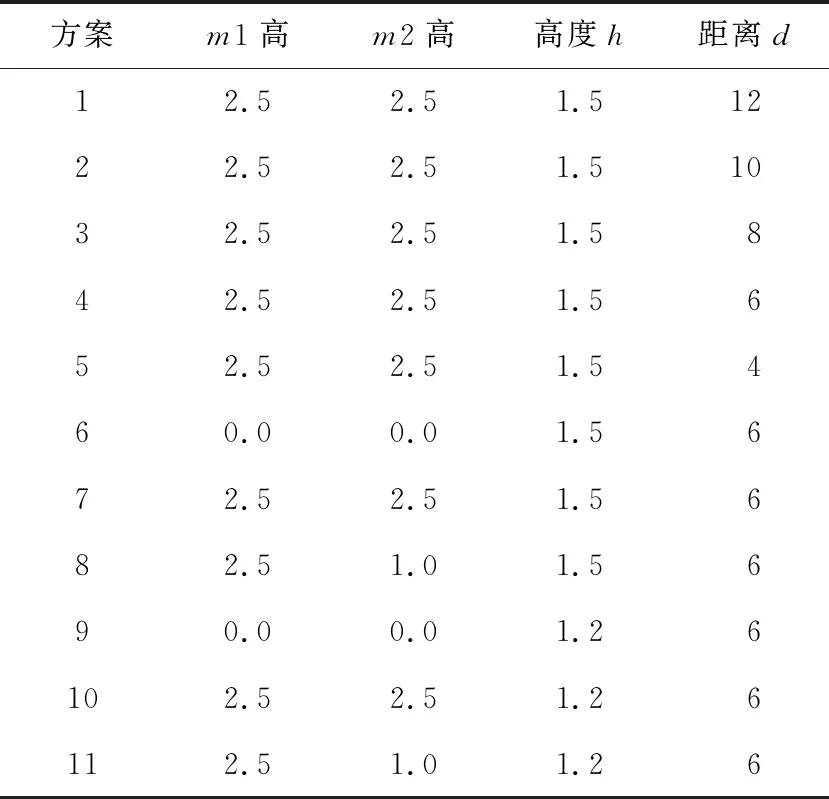
Table 3 Design of experimental scheme表3 实验方案设计 m
别是在摄像机高度、摄像机与信标地面距离d等参数相同的条件下,观察信标高度的变化对定位误差的影响;方案6~11是在信标高度、摄像机与信标地面距离d等参数相同的条件下,观察摄像机高度变化对定位误差的影响。表4是11套方案的测试结果统计分析。由表4可知,所有方案的定位误差都在1 m以内,且均值在0.5 m以下,在d为12、10 m时出现过误差较大的情况。从方案1~5的结果来看,距离d对误差有较为明显的影响,即平均误差随着距离d的增大有增大的趋势,并且误差波动较大;分别从方案6~8、方案9~11的结果来看,信标高度的变化对测试误差没有明显的影响;从方案6~11的结果比较来看,摄像机高度变化对定位误差没有明显的影响。
4.3 定位坐标的选择
根据3.1节中fm1,m2(γ)=0可求得n个俯仰角γ,根据信标m1、m2可以求出2n个定位坐标,

Table 4 Error statistics results of 11testing schemes表4 11套实验方案的测距结果误差统计
利用DNN模型对最佳定位坐标作出判断。本文以方案1的10次采样结果为例评价DNN的有效性。由表5可知,根据信标m1、m2求得的4个定位坐标可以分为2类,坐标1和坐标2在信标m1和m2的同一侧,坐标3和坐标4在信标m1和m2的另一侧。通过DNN判断可以将坐标1和坐标2作为真实选项挑选出来,但很多时候(编号1、2、3、4、5、6、7、8、10)由于坐标1和坐标2的预测结果相同,DNN也难以抉择,此时本文选择依据最大俯仰角计算的定位坐标(即坐标2)。
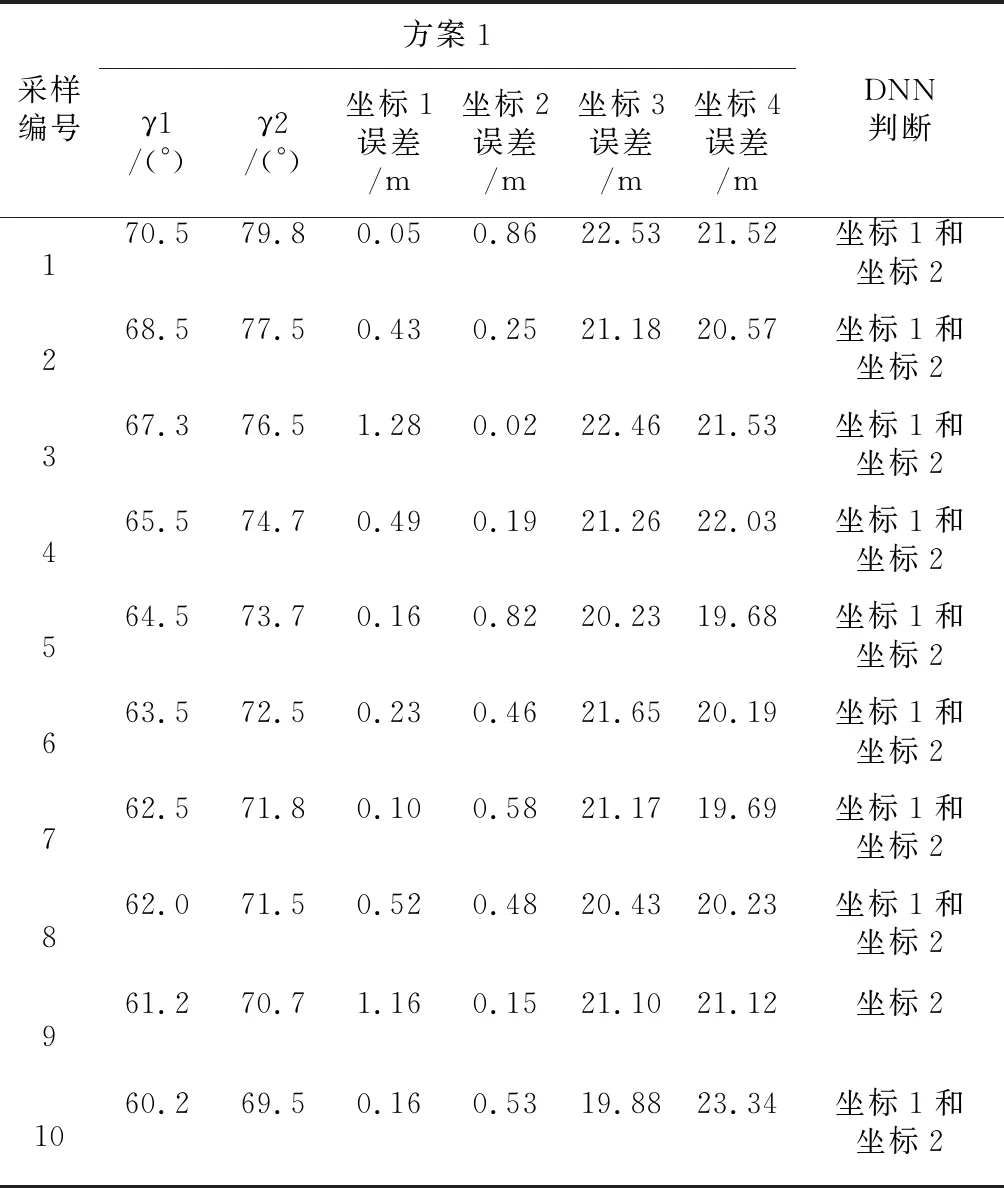
Table 5 Positioning coordinate analysis of 10 samples表5 10次采样的定位坐标分析
4.4 与其他算法的对比
本文选取Horus[22]、Argus[11]和CLIKLoC[23]3个典型的定位算法进行比较。Horus算法是单纯依赖RSS的经典方法,Argus和CLIKLoC算法是近年来利用视觉线索增强定位比较成功的算法。从图4来看,本文算法在定位精度方面明显优于Argus和Horus,略优于CLICKLoC。

Figure 4 Positioning errors comparison of among 3 algorithms图4 3种算法的定位误差比较
5 结束语
本文利用单目视觉测距和三边定位法获得观察点的多个虚拟定位坐标,然后通过对WiFi场景信息进行计算判别获得真实的定位坐标值。在大型商场的大量实验验证了算法的可靠性和稳定性。从实验结果可知,观察点与信标的较远距离(>10 m)是影响定位精度和稳定性的主要因素。在室内合理布局信标可以有效缓解这个问题,因此本文下一步的工作是研究如何布局信标。

