方差辗转的软集参数约简算法*
林连海,田立勤,2,蔡铭楷,李升宏
(1.青海师范大学计算机学院,青海 西宁 810008;2.华北科技学院计算机学院,河北 廊坊 065201)
1 引言
随着科技的发展,大数据时代的到来,人们需要研究的数据关系变得更复杂,对系统的要求也越来越高。不论是在管理科学、社会科学还是工程应用中,都存在着诸多不确定的因素以及不确定的问题,若使用传统的定量分析来处理这种不确定性问题,常常得不到想要的效果。最初,学者们利用概率论来研究数据的不确定性,但概率论不易直接用于决策中,需要对其进行一定的拓展。在此之后,各国学者考虑到现实世界的环境,提出了各种处理不确定问题的理论,较为经典的理论有模糊集[1]和粗糙集[2],这2个理论都可以看成经典集合论上的一个延拓。由于这2个理论具备一定的局限[3],1999年Molodtov提出了软集[4],随后学者们对其展开了研究,规定了软集的运算规则,创建了软集的多种形式[5 - 7],并将软集用于现实决策中[8,9]。近年来,模糊软集的概念和运用正被进一步推广[10,11]。
软集参数约简的定义经历了诸多变化,文献[8]将软集理论用于决策,并进行了软集的参数约简,文献[12]对其参数约简方法进行了改进,直到文献[13]提出关于软集的常规约简NPR(Normal Parameter Reduction)的概念,并提出了参数约简的一种可行方法。
软集参数约简的方法有很多种,经典的有:NPR算法、NENPR(New Efficient Normal Parameter Reduction)算法[14]、0-1线性规划(0-1 Linear Programming)算法[15]、基于群体智能算法的粒子群约简算法[16]、基于去重思想的约简算法[17]和基于局部搜索的算法[18]等。
而概率论的诞生可追溯到16世纪,它是研究自然和人类社会中随机现象的规律的数学分支,目前广泛应用于自然科学、经济学、医学、工程、金融保险甚至人文科学中。人们最早用于处理不确定数据的理论就是概率论。
本文将概率论和软集进行结合,将方差的概念和性质用于软集的参数约简问题之中,提出了适用于大数据背景下的约简算法——方差辗转法,用以解决软集约简参数的问题。
2 基本概念
定义1[13]设集合U={u1,u2,…,un},集合E={e1,e2,…,em},如果映射F能将集合E映射到全集U的幂集中,则称(F,E)是在全集U上的1个软集。其中,E一般称为属性集或元素集,而U一般称为全集,实际背景下,E一般是U的属性描述,为了区别于集合论中全集的概念,本文给U取了1个别名,称其为物集。因此,软集(F,E)可以看成是某个属性与具备这个属性的物集的子集的对应关系。如,对于e1,如果U中具备这个属性的元素有u1,u3,u5,则F(e1)={u1,u3,u5}。我们通常也用F(u,e)=1或F(u,e)=0来表示u是或不是F(e)的元素,因此1个软集可以用1个二值矩阵进行表示(示例见后文表1)。
定义2[15]定义物集元素u的支持集supp(u)为集合{e∈E|F(u,e)=1}。u的支持集的基数记为σE(u),σE(u)=|supp(u)|=∑e∈EF(u,e)。当E为属性集全集时,对应于表格中1行的和。
定义3[13]对于软集(F,E),设R⊆E且R≠∅,若R满足:
σE-R(u1)=σE-R(u2)=…=σE-R(un)
则称R是软集(F,E)的1个常规约简。我们称E-R是可约简集。在所有常规约简中,使可约简集基数最大的常规约简称为最佳常规约简,记为Rmax,对应的可约简集称为最佳可约简集。
定义4约简稠密度ρ=|E-Rmax|/|E|,即最佳可约简集的基数与总属性集的基数的比值。
定义5设软集(F,E)的属性集E={e1,e2,…,em},A⊆E且A≠∅,定义行和的集合:SA={σA(u1),σA(u2),…,σA(un)}。
3 概率论与软集
由于概率论在诸多资料中都能参考,在此不加证明地给出以下定义和引理,并定义软期望和软方差,给出概率论与软集结合得出的一些结论。
定义6(期望) 设X为1个离散型随机变量,X的分布列给出了随机变量X的所有可能取值及概率,则X的期望就是X所有可能的取值相对于当前取值概率的加权平均,记为E(X)。期望反映了随机变量的平均取值大小。
定义7(软期望) 将期望与软集结合给出此定义。对于软集的属性集E={e1,e,…,em},A⊆E且A≠∅,将其行和SA视为随机变量,SA的期望E(SA)称为软集(F,E)在属性集A下的软期望。软期望用于描述物集在属性集A下的支持集的平均大小。结合期望和软集的常规约简的定义,若1个属性集是可约简的,则其每1个物集元素的支持集大小都是相同的,对应于矩阵则表示其行和是相等的。
定义8(方差) 方差定义为var(X)=E[(X-E(X))2]。方差提供了随机变量X在其期望周围分散程度的1个测度。
定义9(软方差) 将方差和软集结合给出此定义。对于软集(F,E),令A⊆E且A≠∅,将其行和SA视为随机变量,其方差var(SA)称为软集(F,E)在属性集A下的软方差。软方差用于描述物集在属性集A下的支持集大小的离散程度。根据方差的定义,可知当软方差为0时,SA中的元素是全相等的,即属性集A是可约简集,E-A是1个常规约简。可见,软方差能用于描述1个属性集是最佳可约简集的子集的可能性大小:软方差越大,则该属性集是可约简集的可能性越小。
定义10(0-1分布) 对于1个事件而言,只有2种结果,当其发生的概率为p,而不发生的概率为1-p时,我们称其服从0-1分布,且各属性之间是独立的(实际上,可约简集中的属性不是独立的,这里主要是为了方便讨论而简化了模型)。
引理1设Qn为n个独立的随机变量X1,X2,…,Xn的和所构成的序列,定义:
Qn=X1+X2+…+Xn
则由独立性有以下关系:
var(Qn)=var(X1)+var(X2)+…+var(Xn)
引理2var(X)=var(X+k),k为常数。
根据上述理论,可推导得出以下结论:
定理1假设软集(F,E)的每个属性之间是完全独立的,A⊆E,B⊆A,即A是1个属性集,B是A的1个真子集,则能推导出var(SA)≥var(SB)。换言之,若软集(F,E)的每个属性之间是完全独立的,从属性集中随机选取的元素越多,那么对应的软方差也就越大。
证明由于B⊆A,设A-B=C,根据引理2,有:
var(SA)-var(SB)=var(SC)
又方差是不小于0的,故
var(SA)-var(SB)≥0
得到结论。
□
定理2设A为可约简集,A′为从A中减少1个元素e的集合,当元素e对应F(ui,e)不是全0或全1时,i=1,2,…,n,有var(SA) 证明设随机变量Y1,Y2,…,Yn服从于0-1分布,对应于取自可约简集中的n个属性,记Y为其和所构成的序列,对应于软集中的行和,有var(Y)=0,且对于任意物集元素u都有: Y1+Y2+…+Yn=E(Y) 定义Qn、Pn如下: Qn=Y1+Y2+…+Yn Pn=Y1+Y2+…+Yt-1+Yt+1+…+Yn 即Pn为Qn中去除1个属性后的n-1个独立分布的联合分布,可得到Pn实际是服从E(Y)-Yt分布的,即var(Pn)=var(E(Y)-Yt),据引理2有: var(E(Y)-Yt)= var((-Yt)+E(Y))=var(-Yt) 由定义7知var(-Yt)=var(Yt)。综上,即从约简集中删除1个属性后,其所得集合的软方差会等于被删除的属性本身的方差,由于可约简集的方差为0,当被删除的属性不是全0或全1的属性(也就是方差不为0)时,var(Pn)会大于var(Qn)。 □ 注:上述理论是在大样本情况下的,只有在样本数足够大的时候,方差和期望才有意义。后文算法思想也是在大样本的条件下讨论。 当今世界对于数据的获取是相对容易的,各公司、机构的数据库中,通常都有成千上万条数据,因此可以认为软集矩阵在某个属性上是服从0-1分布的。本文将贪心算法、概率论与软集结合,给出一个在大数据背景下使用的软集参数约简算法——方差辗转法。 假设软集(F,E)中所有的属性之间都是独立的,设一个任意的可约简集表示为Xr={Xr1,Xr2,…,Xrq},再设任意的最佳常规约简的子集Xm={Xm1,Xm2,…,Xmw},则属性集的任意幂集可写成E′=Xr+Xm,由于Xr可约简,知SE′=S(Xm+Xr)=SXm+Kr(Kr为常数),据定理1,如果属性集变大,对应的行和的集合SE′的方差会增加。即有以下2个结论: (1)在Xm中,如果删除1个属性,SE′的方差会减少。 (2)在Xr中,如果删除1个属性,SE′的方差会增加。 综上可以得到这样1个结论:在1个属性集中,如果删除1个属性,得到的剩余属性集的软方差如果变小了,那么这个属性很可能是约简集中的属性。考虑极限情况,当样本数量足够多时,在1个属性集中如果删除1个属性,软方差变大的一定是最佳常规约简中的属性,而软方差变小的一定是最佳可约简集中的属性。 另外,从定理1可以看出,当var(SC)等于0时,有var(SA)=var(SB),也就是说对任意的属性集,从中增加或删除软方差为0的属性集不会对整体的软方差有任何影响。当SC中仅有1个属性的时候,即属性为全0或全1的属性时,是需要特殊处理的,需要将这种属性包含到最佳可约简集中。 参照二进制蚁群算法中的概念[19],给出如下定义。 设有向图G=(V,I),顶点集为V,边集为I,其中,V={v0,v1,0,v2,0,v2,1,…,vN-1,0,vN-1,1,vN,0,vN,1},v0表示起始顶点,vi,0和vi,1表示二进制码串中bi位取0或取1的顶点。对软集而言,N表示属性集个数,设软集的属性集为E={e1,e2,…,em},bi位取0表示当前属性集不包含ei,取1表示包含ei。如图1所示,为了表示方便,将vi,0与vi,1合并表示。我们将这样表示的1个0/1二进制码串称为1条路径。 在此结合软集的参数约简给出解释:对于1个物集大小为n,属性集大小为m的软集(对应的二值矩阵是n×m规模的),构建1个长度为m的二进制串,表示1条路径,同时,用这条路径表示1个候选的可约简集。该二进制串上的1个0/1值被称为路径的1个节点,每1个节点只能取0或者1,当第k个节点取1时,表示当前的候选可约简集包含第k个属性,这样就可以用1个二进制串来表示软集的1个候选可约简集。 例如,设软集的物集大小为5,属性集大小为6,假设其第1、3、4个属性元素构成了1个可约简集,那么这个可约简集对应的路径就是[1,0,1,1,0,0]。 Figure 1 Schematic of the path图1 路径示意图 步骤1初始化路径L,使其节点取值全为1。 步骤2计算路径L对应属性集子集的软方差var1。 步骤3对路径L进行遍历,对所有取值为1的节点做如下操作:从L中删除该节点(即将码串中的对应位置设为0),计算对应的软方差,还原路径L(取消删除操作)。 步骤4记录步骤3得到的软方差的最小值var2,以及其对应的节点位置。 步骤5var2如果为0,则从路径L中删除步骤4得到的节点,此时L对应的属性集即为最佳可约简集,最后计算并返回最佳常规约简集,结束算法。 如果var2>var1,则说明当前已经是方差辗转法能得到的最优结果,方差辗转法失效,退出算法。 如果var2 上述算法在执行的时候,经常可能陷入局部最优解,这通常是由于样本数量不够大,运用概率统计中的理论时会产生一定的误差,因此算法需要有一定的容错率。在此进行如下考虑:在算法执行的初期,矩阵中包含许多相似程度较大的属性列,在这样的情况下,方差辗转法很可能会错误地删除可约简属性对应的路径节点。假设方差辗转算法执行结束,算法失效,没有得到结果,这时记录的路径中实际只是少了最初删除的这个节点时,我们希望能将一开始误删除的节点重新加入到路径中,故考虑增加节点的方法。 由定理2可知:如果可约简集中减少1个属性,软方差一定会增加。根据这个结论可以推出:对1个可约简集的真子集,增加1个不属于这个真子集的可约简属性,软集在这个真子集上的软方差一定会缩小,因此将步骤3修改如下: 步骤3对路径L进行遍历,对每1个节点进行如下操作:取反(即如果是1则改为0,如果是0改为1),计算软方差,还原路径(取消取反操作)。 方差辗转法流程图如图2所示。 Figure 2 Flow chart of variance toss algorithm图2 方差辗转法流程图 假设软集的矩阵规模是n×m,则对路径进行1次遍历的时间复杂度可分成2部分:1部分是计算方差,其时间复杂度和物集大小n成正比,即O(n);另1部分,每次迭代要计算当前路径对应的属性集的行和,这个操作的时间复杂度也是O(n)(在程序实现时,先求出未操作前的行和,每次只需从这个行和中减去或加上软集矩阵的1列即可),每次迭代需求方差m次,故1次迭代的时间复杂度为O(m×(n+n))=O(mn)。 在没有修改步骤3之前,迭代次数不会超过m,修改步骤3后,虽然不能确定迭代次数,但是其软方差是在不断减小,可以认为其不会超过2m(在实验时,对于1个已删除节点,后期可能会再加入可约简路径,但是没有出现再次删除的情况)。故整个算法的时间复杂度为O(m2n)。 而0-1线性规划是整数规划的一种,属于NP难问题,虽然随着运筹学的发展,出现了许多优化的算法[20],但这些优化依旧不能使0-1线性规划问题在多项式时间内计算出结果。 由此可见,从时间复杂度上来说,方差辗转法优于0-1线性规划法。 为了说明方差辗转法的计算过程,将文献[17]中给出的软集数据作为示例,使用方差辗转法进行参数约简。 实验数据如表1所示,数据规模为35×16,表1中每1列对应软集中的1个属性元素,每1行对应软集中的1个物集元素。 对表1中的软集使用方差辗转法,计算过程如表2所示。 第5节使用方差辗转法进行了1个简单的实验,展示了算法的运行具体流程,在本节将使用大规模的随机数据进行实验,以比较2种算法的效率以及准确度。 数据测试的运行环境都是MacBook Air(13-inch,2017),使用的编程软件是Matlab R2017b,运用Matlab中的随机数生成软集矩阵进行实验。本文共给出了4个数据测试结果:物集倍数(物集大小与属性集大小的比值)对运行效率的影响曲线、物集大小对运行效率的影响曲线、约简稠密度大小对运行效率的影响曲线和属性集大小对运行效率的影响曲线。实验结果表明,方差辗转法在大数据背景下,运算效率高于0-1线性规划法。 实验使用的数据是由Matlab随机生成的, 其中物集大小从属性集大小的3倍到100倍变化,每次随机5组数据求平均值,共1 470组随机数据。 实验结果如图3所示。 可以看出,物集的倍数越高,方差辗转法的运算效率越高,运算时间相比于0-1线性规划算法有大幅度缩短。 根据实验结果可以计算出,当物集大小是属性集大小的100倍,约简稠密度 (见定义4)为0.1时,0-1线性规划的运行时间大约是方差辗转法的20倍,而约简稠密度是0.5时,前者大约是后者的30倍。 大数据时代,数据库中1个有50多个字段的表通常会有上万条记录,即物集大小是属性集大小的百倍甚至以上时,本文算法的时间效率比0-1线性规划法的高很多。 实验使用的是属性集大小为100、约简稠密度为0.5的随机数据,物集大小从50~1 000递增,共4 755组随机数据。实验结果如图4所示,其中,图4a是全数据的实验结果,图4b~图4d是对全数据某一部分的放大。 Table 1 Example of soft set matrix表1 示例的软集矩阵 Table 2 Example calculation procedure表2 示例的计算过程 从图4a来看,方差辗转法和0-1线性规划法的运算效率相差不大,在同1个数量级。 Figure 3 Influence of the multiple of the universal set size图3 物集倍数的影响 Figure 4 Influence of universal set size图4 物集大小的影响 图4b是物集大小是属性集大小的0.5~1倍时的实验结果。在这种情况下,方差辗转法几乎得不到结果。但同时,0-1线性规划法也会出现很难得到结果的情况(虽然从统计图上看有运行时间结果,这是因为程序中对0-1线性规划设计了时间限制,当超出这个时间时,算法会直接结束),特别是属性集大小正好是物集的2倍时,0-1线性规划法经常在可接受时间内得不出结果。例如,对于规模为100×200的随机软集,0-1线性规划法在MacBook Air (13-inch,2017上)连续运行2个小时(Matlab默认最大运行时间),依旧得不到结果。 从图4c可以看出,随着物集大小的增加,方差辗转法逐渐生效,物集大小达到属性集大小的2倍后,没有出现过约简失败的情况。 图4d和图3结论一致,说明在大数据背景下,方差辗转法是优于0-1线性规划法的。 实验使用的属性集大小为200的随机数据,选取物集的大小分别为400,600和800,统计约简稠密度对算法效率的影响。实验结果如图5所示。 从图5可以看出,约简稠密度对方差辗转法的影响很大,但是对0-1线性规划法几乎没有影响。同时从图5a和图5b可看出,方差辗转法存在着缺点:即使当物集足够大时,如果约简属性不够多,也可能出现约简失败的情况(实际上在图5a和图5b中,分别有1 500次测试,各出现了1次约简失败的情况,图5c中没有出现约简失败,其实在约简稠密度极低的时候,参数约简的实际意义就不大了),这说明算法仍有需要改进的地方。如果约简稠密度足够高,方差辗转法会优于0-1线性规划法,并且从图5中能够看出,方差辗转法的运行时间与约简稠密度基本成反比。 实验使用的数据为:属性集大小从50~400递增,共1 755组随机数据。实验结果如图6所示。 从图6中可以看出,方差辗转法和0-1线性规划法的运行时间相差不是很大,在属性集较小时,方差辗转法优于0-1线性规划法,但是当属性集增大时,方差辗转法运行时间就会超过0-1线性规划法的,属性集继续增大,方差辗转法会出现约简失败。 Figure 5 Influence of reduction density图5 约简稠密度的影响 Figure 6 Influence of attribute set size图6 属性集大小的影响 本文将软集和概率论结合,提出了一个应用于大数据背景下的软集参数约简算法——方差辗转法,对于n行m列的软集矩阵,此算法的时间复杂度是O(m2n)。 实验表明,在物集足够大的时候,方差辗转法的效率超过0-1线性规划法的效率。算法的实现环境要求简单,不需要依赖于Matlab等特定的运行环境;运行机制明了,实现起来极为简单;实现过程中,大部分运算时间都用在了向量计算上,这非常利于并行计算的设计,效率还有进一步提升的空间。 当然方差辗转法还有许多需要完善的地方,例如概率模型的建立以及模型在概率论上的理论解释等等。概率论与软集的结合以及概率论与贪心算法的结合都是本文的创新点,同时也是值得研究的方向。4 方差辗转法
4.1 算法思想
4.2 路径

4.3 算法实现步骤
4.4 现实背景下的改进
4.5 算法流程图

4.6 时间复杂度分析
5 实验
5.1 实验数据
5.2 实验结果
6 算法对比及分析
6.1 物集倍数的影响
6.2 物集大小的影响




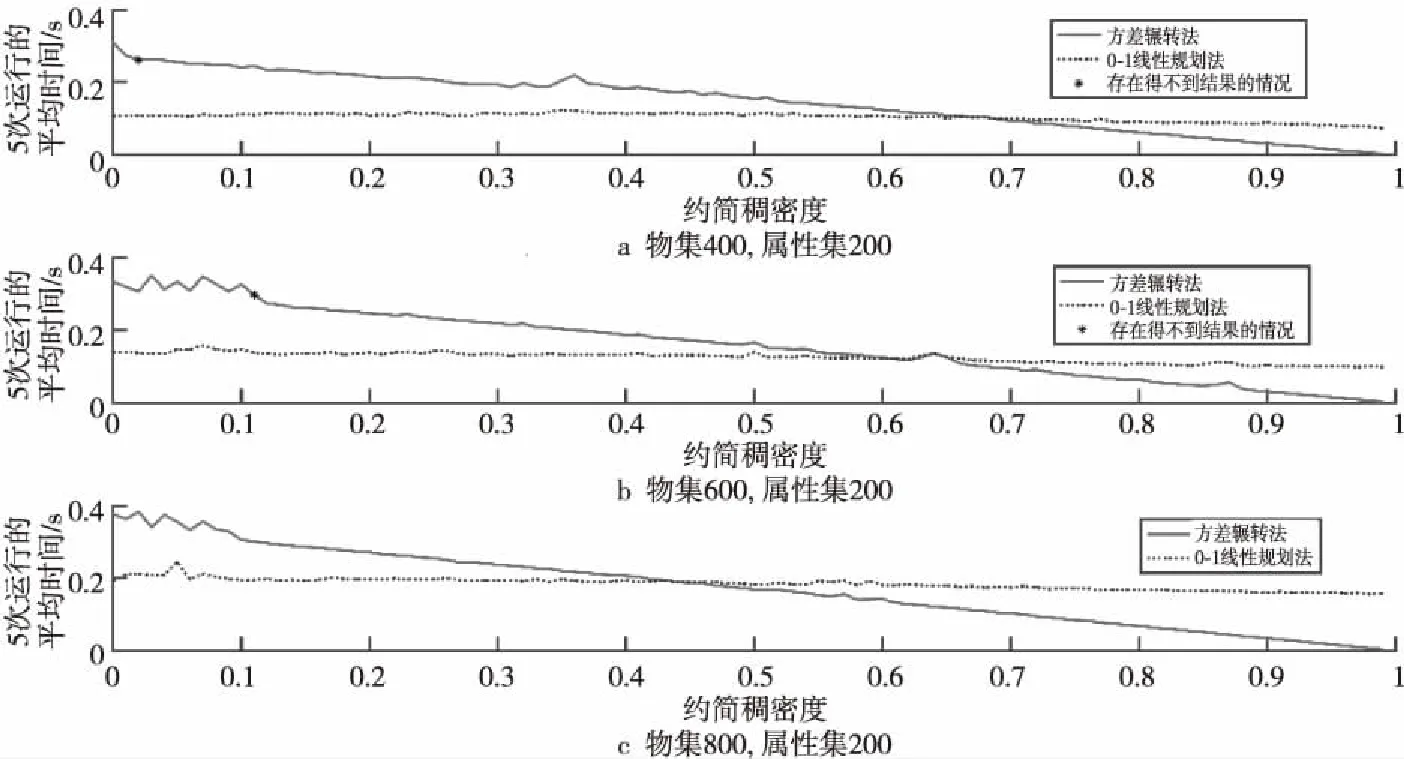
6.3 约简稠密度大小的影响
6.4 属性集大小的影响

7 结束语

