新型装配式密肋楼盖四边简支的受弯承载力

(1. 济南大学土木建筑学院， 山东济南250022； 2. 山东建勘集团有限公司， 山东济南250000)

密肋楼盖以其自重轻、适应大跨度结构使用、结构合理等特点在土木工程中应用较为广泛，国内外学者对该类楼盖的研究也取得了许多成果。Aguado等[1]提出了一种关于预应力空心楼盖的热力耦合模型，并与标准火灾试验进行对比，验证了该模型在失效机理和失效时间方面的有效性。沈蒲生等[2]通过设计四边简支条件下双向密肋楼盖大比例模型试验,提出了极限承载力和极限变形计算方法。王兴肖等[3]研究了垂直均布荷载作用下空腔构件的楼盖模型试验,并结合现浇密肋梁和空腔构件间的协同作用机理,提出了合理、 简化的设计方法。李培林等[4]通过对大量实际工程的分析，提出针对不同类型密肋楼盖的跨中弯矩、跨中剪力和跨中挠度计算公式，在此基础上编制了《混凝土密肋及井式楼盖设计手册》。通过模型试验数值模拟和Timoshenko梁剪切理论， 黄川腾等[5]研究了剪切变形对空心楼盖箱型构件挠度所产生的影响， 并基于剪切刚度相等理论进一步提出了挠度修正方法和剪切模量取用方法。 汪幼林[6]、 吴方伯等[7]通过对9 m×9 m(长度×宽度)密肋空心楼盖的试验研究， 提出了密肋空心楼盖的承载力和挠度实用计算方法。 Aguado等[8]通过改变钢筋布置方式， 对4种预应力空心楼板高温下的抗弯性能进行研究， 结果表明， 当钢筋从受火面剥离后， 根据欧洲混凝土抗火设计规范(EC2-1-2规范)求得的抗弯承载力偏大。Venanzi等[9]对4块采用轻质高强圆柱形填充的空心楼盖进行了全尺寸抗火试验和数值模拟分析，结果表明，当混凝土因高温而剥落时，承载力发生明显下降。Shakya等[10]对6块预应力空心楼盖进行了受火试验和数值模拟，结果表明，空心楼盖在标准设计的火灾条件下可承受荷载2 h，通过试验数据建立的有限元模型能很好地反映预应力空心楼盖在高温下的工作性能。王杨等[11]采用数值模拟、拟梁法和拟板法3种计算方法对某广场工程中的大跨度现浇空心楼盖进行计算和分析，通过对计算结果进行比较，认为整体计算有限元模型能够真实模拟构件的边界条件。以上研究成果多以传统装配式空心或肋梁楼盖为研究对象，为了适应建筑工业化的行业发展趋势，对新型装配式密肋楼盖的需求越来越大。

由于目前尚没有针对新型装配式密肋楼盖的力学分析模型和承载力计算方法，因此，本文中针对提出的新型装配式楼盖，在现有设计理论的基础上，结合ABAQUS软件进行数值研究，旨在找到一种适用于新型装配式密肋楼盖的计算方法，为新型装配式密肋楼盖实际应用推广提供理论基础。

1 楼盖模型

为了适应当前装配式建筑的发展需要，本文中提出一种装配式钢筋桁架密肋楼盖，以预制钢筋桁架作为肋梁钢筋骨架，在面层混凝土中配置钢丝网，肋梁间采用轻质泡沫混凝土块作为填充物形成密肋结构，预制钢筋桁架现场装配，在节点处采用特殊连接件连接，配以装配式铝合金模板，只需要在现场浇筑免振捣混凝土，可同时保证施工质量和速度。填充的泡沫混凝土和浇筑的面层混凝土厚度可根据具体需求以及楼面荷载选择合适的厚度。楼盖三维模型如图1所示。

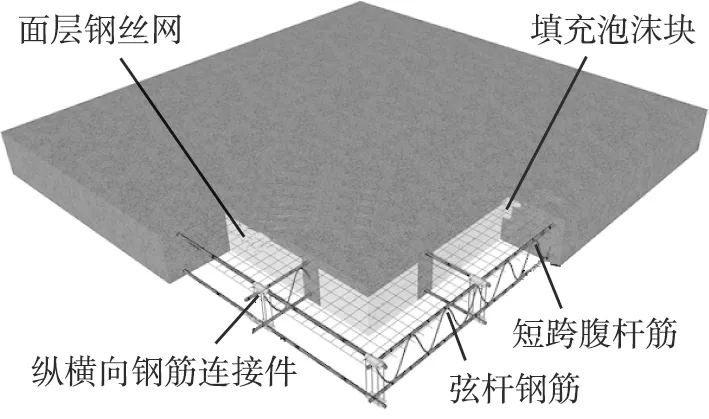
图1 新型装配式密肋楼盖三维模型

2 计算理论

目前关于密肋楼盖的实用计算方法主要有交叉梁系法、双向板法、基于弹性力学的拟板法。

2.1 交叉梁系法

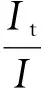
(1)

式中s、r分别为肋梁截面高度、 宽度。

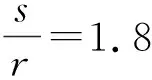
对于其他类型楼盖的计算， 《混凝土密肋及井式楼盖设计手册》中提供了不同跨度、 尺寸密肋楼盖在不同边界、 荷载时的弯矩、 剪力和挠度计算系数。

2.2 双向板法

采用双向板法计算密肋楼盖时，通常将密肋楼盖当作受拉区被挖去一部分混凝土的实心楼盖，计算截面也变为T形截面，这样计算时就可以按照求解实心双向楼盖的计算思路及方法进行。四边简支的钢筋混凝土密肋楼盖挠度变形如图2所示。

a1,a2,…,au—跨度a方向肋梁；u—肋梁编号；b1,b2,…,bu—跨度b方向肋梁； c1、 c2—肋梁间距；af1,af2,…,afu—肋梁a1,a2,…,au的挠度； f—各肋梁挠度；bf1,bf2,…,bfu—肋梁b1,b2,…,bu的挠度。图2 肋梁受力挠度变形示意图

对于四边简支密肋板，按照变形协调条件，计算均布荷载下的内力分配比例以及中间梁的跨中弯矩和跨中剪力，即

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

式中：q1、q2为肋梁分配得到的均布荷载；a、b为楼盖不同方向的跨度；x1为自设变量；q为均布荷载；M1、M2为与跨度a、b方向水平的任一边梁的跨中弯矩；M1u、M2u为与跨度a、b方向水平的中间肋梁的跨中弯矩；c1、c2为肋梁间距；V1u、V2u为跨度a、b方向中间梁的跨中剪力。

根据变形协调条件及密肋楼盖的受力特点， 靠近支座各肋梁的挠度f小于中间肋梁的挠度，因此， 相应的内力值也小于中间肋梁的。 现假定当楼盖截面尺寸相同时， 梁的弯矩值和剪力值与挠度成正比， 这样即可近似求解肋梁内力。 当中间梁最大挠度为afu时， 可设两侧各梁的最大挠度为af1，af2， …，afu与bf1，bf2， …，bfu。各肋梁受力变形情况如图2所示，其中afu=bfu。其余梁如a1、b1的弯矩和剪力分别为

(10)

(11)

(12)

(13)

式中：Ma1、Mb1为梁a1、b1弯矩；Va1、Vb1为梁a1、b1剪力。

若求解其他梁的剪力值与弯矩值，则将相应的最大挠度分别代入式(10)—(13)即可。

(14)

式中：E为弹性模量;I为截面惯性矩。

最大挠度为

(15)

因此，挠度比值为

(16)

2.3 基于弹性力学的拟板法

通过基于弹性力学的拟板法求解密肋楼盖时，需要将双向密肋楼盖按照刚度等效的原则等效成正交各向异性板，然后再利用板的计算公式求解肋梁中的弯矩、剪力和挠度[12]。正交密肋楼盖结构模型如图3所示。

b1、 b2— x、 y方向T型肋梁宽； c1、 c2— x、 y方向肋梁间距； h1+h、 h2+h — x、 y截面总高度。图3 正交密肋楼盖结构模型

将双向密肋楼盖按照刚度等效的原则等效成正交各向异性板需要满足以下2个条件： 1)双向密肋楼盖x、y方向的肋间距均相等； 2)肋梁距离远小于板的纵向长度。等效后x、y方向的抗弯刚度为

(17)

式中Ix、Iy为x、y方向T型截面对中性轴的惯性矩。

为了提高计算精度，由板所组成的横截面部分应除以1-v1v2，其中v1、v2为泊松比。正弯矩计算时肋梁按照T形截面考虑。b1、b2为x、y方向T型肋梁宽，c1、c2为x、y方向肋梁间距，h1+h、h2+h为x、y方向截面总高度。计算设计负弯矩值时，肋梁截面按矩形截面考虑。

c1段截面的形心为

(18)

c2段截面的形心为

(19)

x向惯性矩为

(20)

y向惯性矩为

(21)

密肋楼盖等效抗扭刚度由肋梁和板面2个部分组成，即

(22)

式中：D3为抗扭刚度；G为剪切模量；k为考虑板开裂后梁抗扭刚度修正系数，一般情况下可近似取k=1；Jtx、Jty为x、y方向的抗扭刚度，

(23)

G与弹性模量、泊松比的关系为

(24)

在均布荷载作用下，密肋楼盖结构等效成正交各向异性平板结构后，弹性曲面微分方程为

(25)

式中af为挠度。

通过式(25)可根据不同的边界条件，用理论解或者数值解法得出薄板挠度af的表达式，从而求得弯矩及扭矩，即

(26)

式中：Mx、My为单位板宽内的弯矩；Mxy为单位板宽内的扭矩。

根据式(26)和求得的挠度af，即可求得刚度等效后正交各向异性板的弯矩和挠度。

2.4 算例分析

密肋楼盖等效成正交各向异性平板后，可由式(17)—(26)求得挠度和弯矩。对所求肋梁T型范围内楼板的弯矩进行积分运算，通过所求肋梁的抗弯刚度值与该方向T型截面总抗弯刚度的比值确定积分区域，进而得到所求肋梁分担的弯矩值。

对于x方向，令

(27)

对于y方向，令

(28)

式中：Ixk、Iyk为第k个肋梁x、y方向的惯性矩；Ix、Iy为肋梁x、y方向的总惯性矩，按照式(20)、(21)进行计算。

梁内的弯矩为

(29)

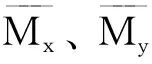
本文中所提到的新型密肋楼盖可等效成四边简支正交异性板，如图4所示。

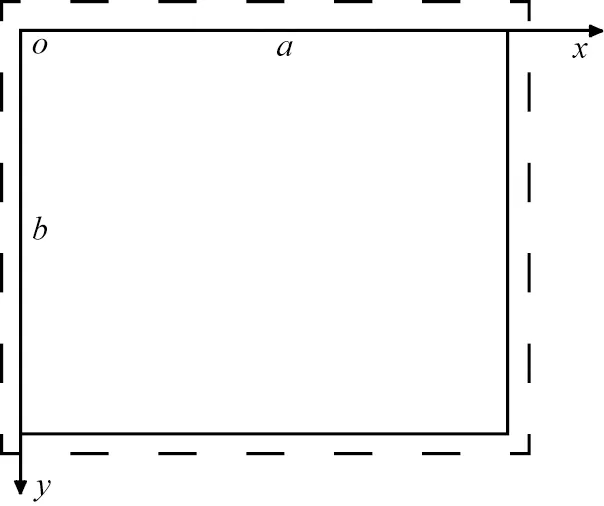
a、 b—板不同方向的跨度。图4 四边简支正交异性板

弯矩计算过程如下。a、b分别为板的跨度，q0为均布荷载，求解此密肋楼盖挠度的挠曲线微分方程函数解为

(30)

式中：m=1,3,5,…；n=1,3,5,…。

单位宽度内弯矩为

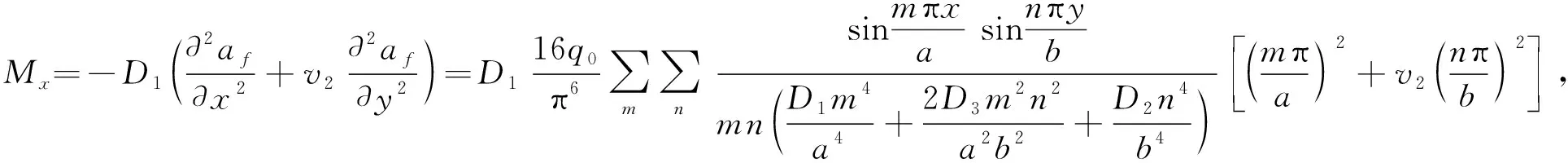
(31)

(32)

肋梁中的弯矩为

(33)

令

(34)

则

(35)

令

(36)

则

(37)

对于具有其他边界条件的板，也可得到类似的解。由于式(37)中所要求解的弯矩值和挠度值不适宜手算，因此，可利用MATLAB软件编制计算程序进行计算。

3 数值分析与对比

利用ABAQUS软件建立一个尺寸为4.67 m×3.47 m×0.22 m(长度×宽度×高度)的装配式钢筋桁架密肋楼盖模型。模型中混凝土采用ABAQUS软件中的C3D8R单元，钢筋骨架和钢丝网采用 T3D2 单元，由于泡沫混凝土块不参与受力，因此该部分在模型中未予考虑。楼盖模型如图5所示。楼盖按照四边简支条件约束进行设计，恒载(自重)取值为3.5 kN/m2，考虑5种实用工况进行模拟，假设各工况下的活荷载分别为 2、 5、 10、 15、 20 kN/m2。以楼盖中部某肋梁跨中弯矩作为该模拟中的研究对象，见图5中的A点，弯矩为Mx。将以上3种方法计算得出的肋梁跨中弯矩值与ABAQUS模拟值对比， 其中相对误差为理论值与模拟值的差值与模拟值之比，结果如表1所示。由表可知，各种工况下基于弹性力学的拟板法得出的结果与有限元法结果吻合度较高，其他2种方法计算值均偏大，尤其是双向板法， 最大误差达到41.42%，精度相对较差。通过分析可以发现，各计算方法的适用性可以从2个方面考虑：从准确率考虑，拟板法得出的结果与有限元结果相比，弯矩最大误差为9.55%， 而其他2种方法理论值均偏大；从计算量考虑，如果采用拟板法对密肋楼盖进行设计，则只需要输入13个数据即可，而用交叉梁系法和双向板法在计算过程中输入参数较多，并且步骤较之基于弹性力学的拟板法也更多更烦琐。综合比较可知，采用修正后的拟板法进行计算，既可以保证精度，又可以减少计算量，在方案的设计初期或者概念设计阶段，具有一定的实用性，也更容易被结构设计人员接受。

A—楼盖中部某肋梁跨中弯矩为Mx的点。图5 新型装配式密肋楼盖有限元模型

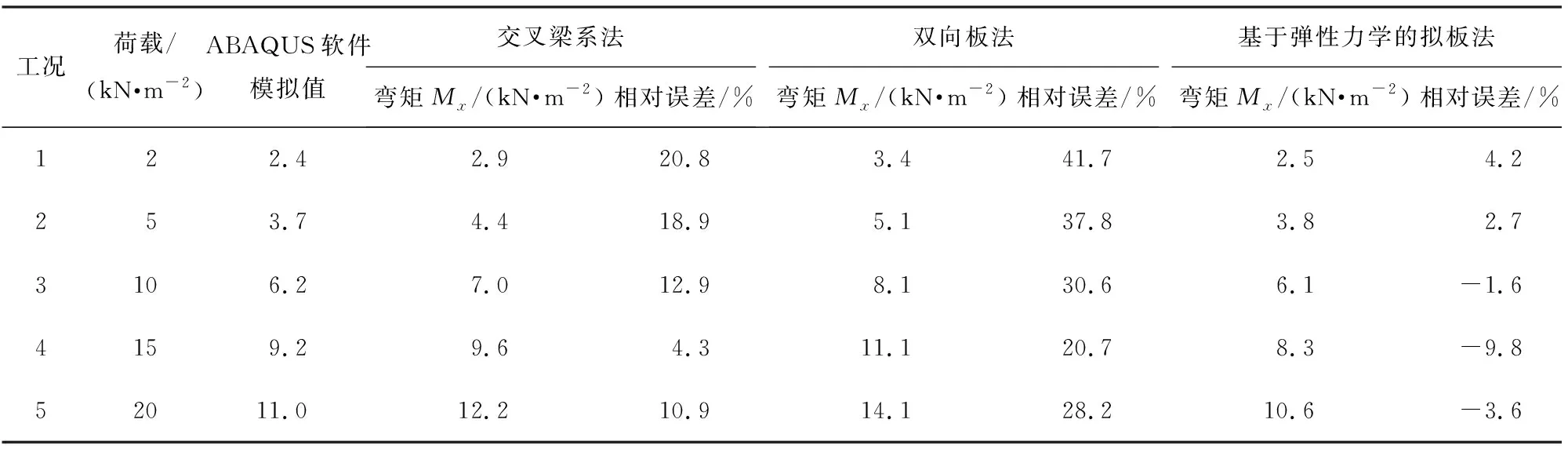
表1 不同计算方法的弯矩值对比

4 结论

本文中针对一种新型装配式钢筋桁架密肋楼盖，分别采用目前常见的几类计算方法，计算了四边简支情况下肋梁跨中弯矩，并通过有限元软件进行了数值模拟，理论值与模拟结果对比发现，基于弹性力学算法的拟板法具有计算简便、精度高等优势，可以作为该新型装配式密肋楼盖内力和挠度计算的理论依据。