建筑材料供需双方基于采购价格的Stackelberg博弈

(江苏大学a. 土木工程与力学学院， b. 财经学院， 江苏镇江212013)

传统建筑材料采购价格受市场的影响较大，供应商与承包商之间缺乏紧密的合作，在材料市场价格出现不稳定波动时，其中一方会采取“敲竹杠”的方式来增加自身收益或减少自身成本，从而可能扰乱我国建筑材料的市场秩序，无法保持建筑材料供应链长期的竞争优势[1-3]。在满足施工进度和质量的基础上，对工程项目成本进行有效控制是当前企业急需解决的问题。

在传统非合作博弈供应链中，承包商首先制定最优订货批量，以减少自身采购成本，但是这对于供应商来讲并不是最优的[4-6]。国内外很多学者对此进行了研究。马慧民等[7]以多供应商、多生产商与多分销商组成的三级供应链为研究对象制订协同计划，根据下游分销商需求情况决定生产商生产批量与原材料采购批量，使整个供应链成本达到最优。张昆等[8]以供求双方为研究对象，在传统需求方确定订货批量的前提下，采用价格折扣的激励措施，在保证不增加需求方成本的前提下，使供应商成本最小化。张玉华等[9]、 张桂涛等[10]针对1个供应商、 1个需求商组成的供应链，利用Stackelberg博弈方法建立价格折扣协调模型，研究表明，当价格折扣在一定范围，供需双方实现供应链系统成本最小化。鉴于建筑材料的特殊性，以上研究还存在一些不足，主要表现为当制定价格折扣时，集中于减小供需双方成本为目标，但是供应商最小成本并不代表获取最大利润。

本文中以供应商与承包商为研究对象，以工程项目承包商最低采购成本和供应商最大年利润为目标函数，构建传统采购模式下供需双方博弈模型及采用价格折扣情况下的Stackelberg博弈模型。供需双方通过博弈来确定价格折扣率的范围以及对应最优订货批量的倍数，目的是减少承包商订货成本，增加供应商利润，使整个供应链系统达到最优。

1 问题描述

建设工程项目材料成本占直接成本的比例大于60%。近年来，建设工程项目所需要的材料，如钢筋、水泥、石料等材料市场面临产能过剩的问题[11-13]。由于市场产能过剩，因此，出现多个卖方对应1个买方的情况。为了研究需要，本文中把多个卖方对应1个买方的情况简化为由单个供应商与单个承包商组成的二级供应链系统，如图1所示。该系统反映出在建筑材料流转供应链中，供应商与承包商都是从追求自身利益最大化角度进行单独决策，因此他们之间的博弈是非合作博弈。

2 供需双方博弈模型

2.1 模型的基本假设

建筑材料流转过程中， 成本博弈是在博弈参与人之间进行的， 为了方便分析， 进行以下假设和说明：

1)研究1个承包商和1个供应商组成的二级供应链，并且博弈参与人都是理性经济人，他们会在既定的条件下作出使自身利益最大化的抉择，双方不会犯非理性的错误，这是参与人的共同知识。

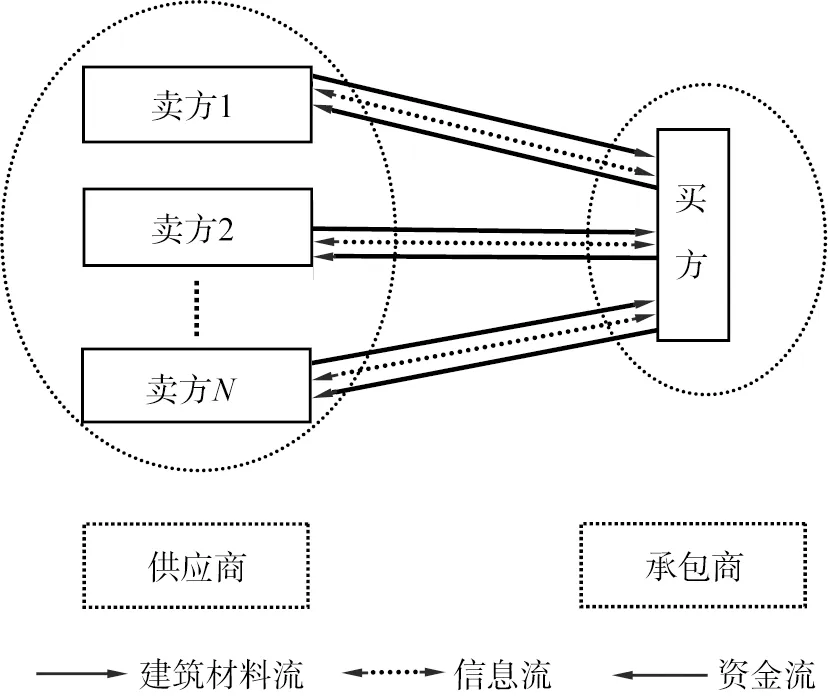
图1 买方主导的供需模型

2)博弈双方间的信息交流是完全畅通无阻的，且行动有先后顺序，后者可以通过观察前者的行动来获取相关信息，作出自己的选择。

3)供应商的年生产力R大于承包商的年需求量D，并且R与D是稳定的。

2.2 传统非合作条件下模型建立与求解

2.2.1 模型建立

在传统非合作条件下，供应商与承包商为了实现各自收益最高或成本最低的目标，都会从自身角度出发制定最优订购批量。在这种供应商生产能力远大于承包商需求量的情况下，承包商为了使自身成本达到最优，不会对供应商让步。此时承包商不需要考虑缺货成本，总订货成本为

(1)

式中：P为单位材料价格；Sc为传统采购模式下承包商单次订货成本；Qc为承包商单次订购材料批量；hc为承包商库存保管费率。

供应商的生产成本模型为

(2)

式中：Bs为单位材料生产价格；Ss为供应商单次运输成本费；n为倍数；As为传统采购模式供应商单次生产准备成本；hs为供应商库存保管费率。

在现实生活中，在买方占主导地位的情况下，供应商为了实现自身利益最大化所设置的最经济生产批量Qs与承包商最优订货批量Qc成倍数关系，即Qs=nQc，此时供应商的生产成本模型与供应商的利润W1分别为

(3)

W1=PD-Cs

。

(4)

2.2.2 模型求解

传统经济订货模型并没有考虑供应商的利益，承包商处于主导地位。为了得到承包商最优订货批量，对式(1)中的Qc求导，可得承包商采用价格折扣后最优订货批量为

(5)

则承包商最小订货成本为

(6)

对式(3)中的Qs求导，可得在供大于求的市场模式下供应商的最优生产批量为

(7)

则供应商的利润W1满足式(4)。

2.3 供需双方Stackelberg模型建立与求解

2.3.1 模型建立

从传统非合作条件下供需双方博弈模型中可以明显看出，在建筑材料承包商占主导地位时，承包商只从自身利益出发，追求自身最优订货批量，使订货成本达到最低；但是，这种订货批量对于供货商并不是最优的，因此提出价格折扣模型，使之降低承包商年订货成本的同时提高供应商年利润，使整个供应链达到最优。

在供应商与承包商的Stackelberg博弈中，供应商是主方，承包商是从方。供应商给予合理的价格折扣，使承包商增大订货批量，通过薄利多销策略提高自身年利润，承包商根据供应商的决策来制定订货倍数。由于价格折扣模式是大批量少次采购，因此承包商的订货批量变为原来的m倍(m>1)，供货商给出价格折扣率α，此时承包商单位材料订货价格降为P(1-α)，由于供应商所给出价格折扣后的售价一般不会低于其成本，因此有

P(1-α)≥Bs，

即

(8)

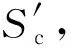
此时供需双方基于价格折扣的Stackelberg博弈模型为

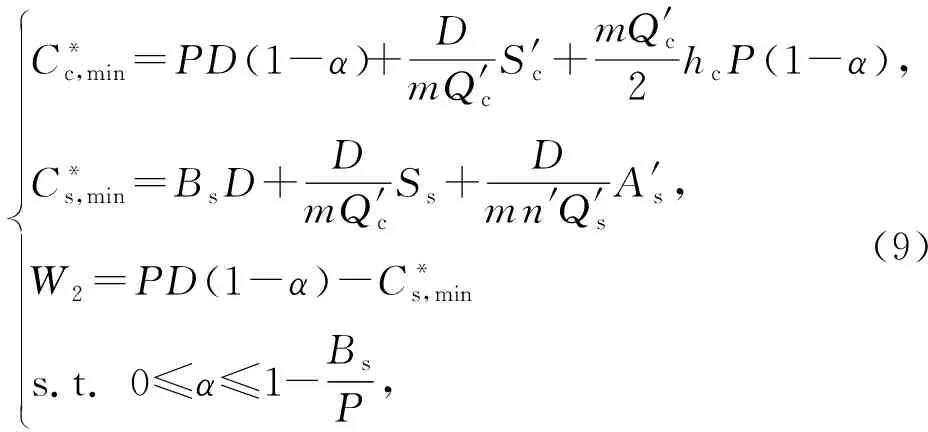
C*c,min=PD(1-α)+DmQ'cS'c+mQ'c2hcP(1-α),C*s,min=BsD+DmQ'cSs+Dmn'Q'sA's,W2=PD(1-α)-C*s,mins.t.0≤α≤1-BsP,(9)

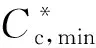
2.3.2 模型求解

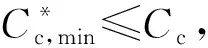
(10)

(11)

从供应商角度出发，当且仅当采用价格折扣进行批量订货的收益大于传统订货收益时，供应商才会采用这种订货模式，即

W2≥W1，

(12)

(13)

利用式(13)对满足W2≥W1所需价格折扣率的范围进行求解，化简式(13)可得

(14)

式(11)、(14)表明，当价格折扣率α满足

(15)

时，承包商与供应商才会愿意采取价格折扣模式。设a为式(15)中α左侧的方程式，称为价格折扣率的下限；b为式(15)中α右侧的方程式，称为价格折扣率的上限。令

c=a-b，

(16)

为了得到a、b、c与承包商订货批量的倍数m之间的关系，对a、b、c关于m进行求导，得

(17)

(18)

(19)

3 模型分析

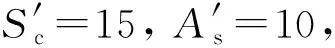
由此可知，c、a与b对m成比例关系，此时c、a与b对m的关系式为

利用Mathematica软件绘制不同坐标系中a、b、c与m的关系，如图2所示。由图可知，当m>1时，b>a>0。由于供应商采取价格折扣后材料单位价格不小于材料单位生产成本时才可能采用价格折扣模式，即1-Bs/P>α>0，并且1-Bs/P>α，1-Bs/P>b，因此只要在[a,b]内寻找任意α值，承包商与供应商就会采用价格折扣模式，达到降低承包商采购成本与增加供应商利润的目的。

a—价格折扣率的下限；b—价格折扣率的上限；c—价格折扣率上下限的差值；m—采用价格折扣后承包商的订货批量为传统采购模型的倍数。图2 a、 b、 c与m的关系

4 模型算例

利用3节中的数据，令P=50，D=500，Sc=20，hc=0.3，Bs=30，R=3 000，hs=0.3，As=50，Ss=20，Sc′=15，As′=10，此时赋予m不同的值，可以得到对应的a、b值，确定α的范围，结果如表1所示。

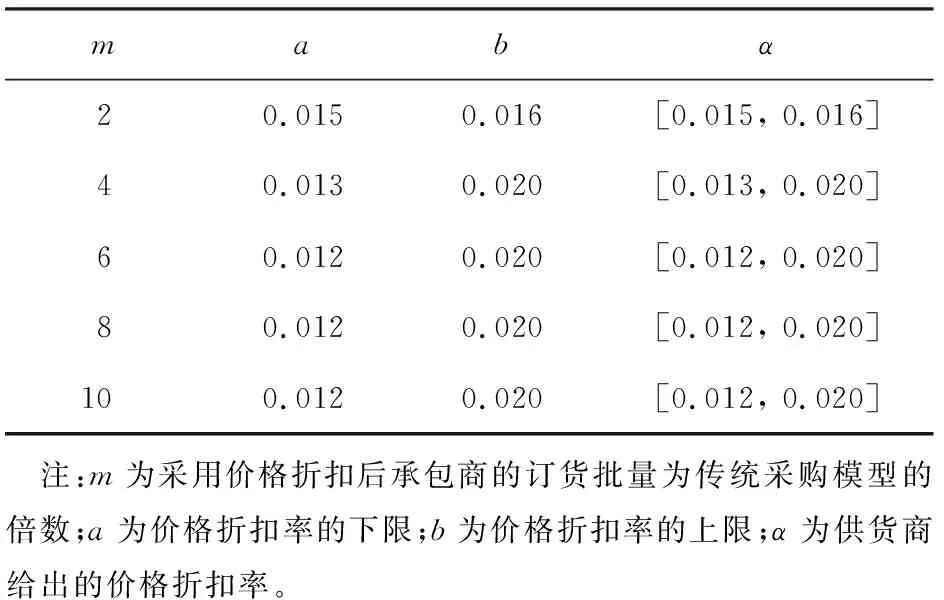
表1 不同m值对应的a、 b值和α的范围

由图2和表1可知，a随m的增大而减小，当供应商给承包商提供合理的价格折扣时，承包商增大了订货批量以减少订货成本，供应商增加年利润。

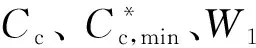
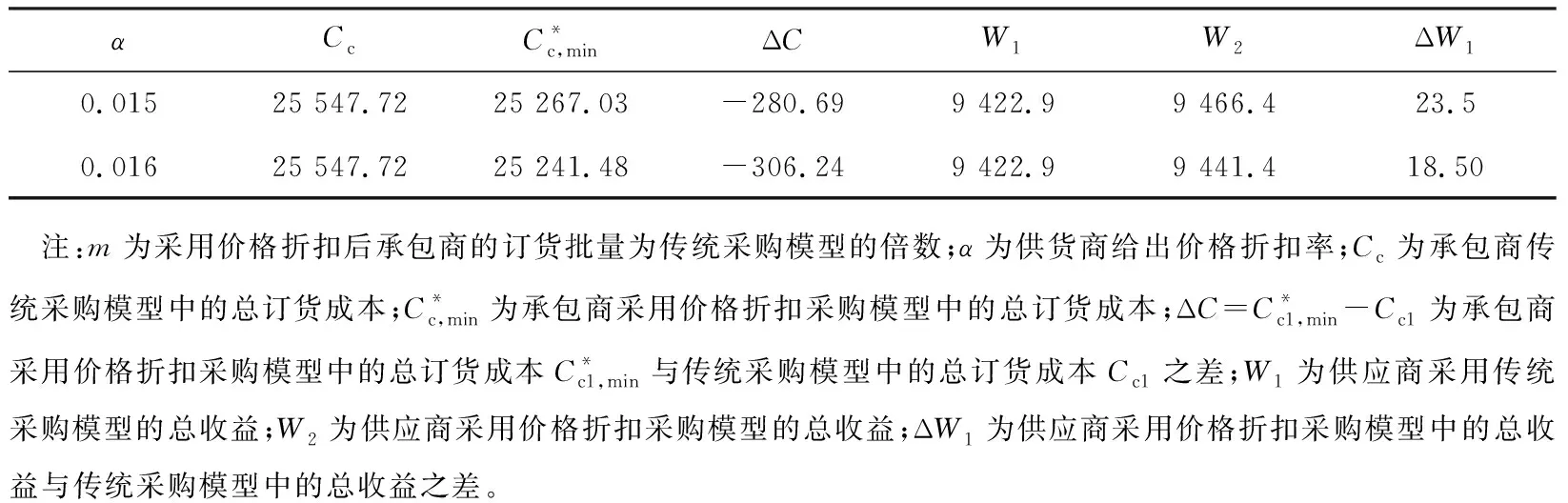
表2 固定m=2时供应商与承包商的相关数据

5 结语

本文中讨论了1个供应商与1个承包商情况下非合作博弈模型，并从供应链系统整体成本与利润角度出发提出了给予价格折扣的Stackelberg博弈模型。得到以下结论：

1)对于承包商，采用价格折扣模式使承包商的订货准备成本减少，从而达到了减少成本的目的。

2)对于供应商，在已知承包商策略的条件下按批生产，减少生产准备成本，清除一切库存，控制了生产成本，增加了利润。

3)对于整个二级供应链系统，供应商采取薄利多销策略增加了年利润，承包商减少了订货准备成本，此时由单个供应商与单个承包商组成的二级供应链系统达到最优，达到了双赢的目的。