斗式提升机物料卸载流动的离散元模拟

(太原科技大学机械工程学院， 山西太原030024)

斗式提升机在垂直输送散料时有其独特的优越性， 因此在粮油、 化工与矿冶领域中得到广泛应用。 在实际应用中， 由于存在机壳磨损、 物料颗粒破碎与回流等问题， 因此需要对提升机的卸料过程进行分析以改善其输送性能[1]。 颗粒流动特征直接决定了斗式提升机结构的设计优化与卸料性能， 因此分析颗粒在料斗内滑移与卸出料斗后的运动过程， 并在此基础上研究颗粒的流动行为[2-5]， 对优化、 改进斗式提升机的生产方式， 提高研发效率具有重要价值。

在斗式提升机卸料过程中，由于物料颗粒是在封闭罩壳内运动，加上颗粒数量多以及颗粒之间、颗粒与机壳之间存在碰撞作用，因此采用传统方法对物料流动行为进行分析非常困难[6-7]。离散单元法(DEM)是一种基于不同本构关系、以牛顿第二定律为理论来处理非连续性介质问题的数值模拟方法，通常采用动态松弛法来求解方程，在散料研究领域应用非常广泛[8]。

Perez-Aparicio等[9]以计算机代码实现的计算公式与结果为依据，获得了特定工况下的料斗最佳几何形状条件，以最大输送距离与最小返料流量为目标，对比讨论了几种料斗形状，得出了料斗的标准设计方法。Holbrow等[10]研究了不同形式的料斗、不同物料、不同工况下的颗粒爆炸压力。McBride等[11]考虑了料斗由竖直过渡为旋转运动时，由料斗连接处尖端引起的颗粒速度阶跃变化，并详细分析了料斗在该阶段的运动行为。Rademacher[12]从理论上分析了卸料阶段料斗内颗粒运动的滑移面特征，推导了颗粒的滑移运动方程，并测试了不同工况下的颗粒流动行为。现有研究侧重于从宏观角度分析颗粒的运动特性，缺乏颗粒流动行为的微观研究。

为了认识斗式提升机物料卸载的流动特征， 本文中采用DEM软件对物料卸载过程进行仿真， 研究颗粒流动轨迹、 速度的分布特点， 对颗粒流动在空间位置上的分布特性进行统计分析， 对比不同工况下每只料斗的生产率， 从而得到卸料效果最优参数组合。

1 斗式提升机颗粒卸载运动过程

按照斗式提升机头轮直径与工作速度的不同，可将其卸料方式分为重力式、混合式、离心式3种。在输送流动性好且不易破碎的粒状、粉状物料时，选用离心式效果较好[13]。离心式卸料是指颗粒在料斗内全部沿着外壁滑动而卸出，此时可把颗粒卸载过程分为2个阶段，一是颗粒在料斗内和料斗间的相对滑动与绕头轮匀速旋转的合成运动，二是颗粒被卸出料斗后的抛物运动。

在重力、离心力与周围物料挤压力作用下，颗粒基于螺旋线分界面由上至下逐层向着料斗前沿流动卸出，处于滑移面以外的颗粒为滑动部分，滑移面以内的颗粒则为相对静止部分。颗粒卸出料斗后，在重力与空气阻力作用下作抛物线运动，其初速度由颗粒在料斗内的滑移运动性质与所满足的边界条件决定，只要求得颗粒的初速度，其运动轨迹即可计算得到。

2 模型建立与仿真

2.1 仿真模型建立

斗式提升机仿真模型结构如图1所示。本文中对模型进行了简化，只保留部分机壳、料斗、胶带与头轮。模型采用8只料斗，间距为200 mm，料斗速度(简称斗速)选取4组(1.0、 1.5、 2.0、 2.5 m/s)。 具体参数如下： 头轮直径为250 mm(满足离心卸料的最小斗速为1.1 m/s)， 机壳宽为246 mm， 头轮轴与机顶垂直距离为329 mm， 头轮轴与机身前壁垂直距离为329 mm， 头轮轴与机罩前壁垂直距离为658 mm。为了进行对比，料斗类型采用深、浅2种，宽度均为110 mm，其平面尺寸如图2所示。

v—为料斗速度。图1 斗式提升机仿真模型结构

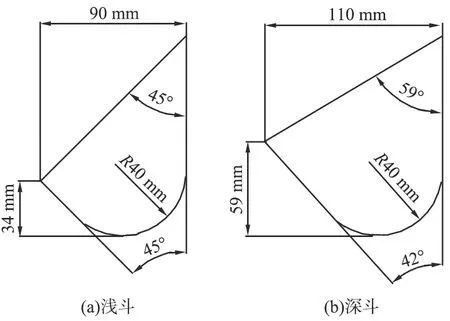
图2 2种类型料斗的平面尺寸

2.2 数值模拟条件

在对卸料过程进行模拟前， 需要进行如下基本假设： 1)忽略颗粒运动所受空气阻力影响， 仅考虑颗粒之间、 颗粒与结构之间的碰撞力； 2)每只料斗内颗粒堆积外形基本一致， 装载颗粒个数均为4 000(实际颗粒装载量误差约为1.1%)。本文中采用DEM软件的Hertz-Mindlin无滑动接触模型， 模拟料斗材料采用低碳钢， 模拟物料颗粒为半径是2 mm的球体， 物性参数分别取低碳钢、谷物的物性参数。取固定时间步长为瑞利时间步长的25%，仿真网格尺寸为颗粒半径的2倍。料斗卸料过程仿真参数如表1所示。

表1 斗式提升机料斗卸料过程仿真参数

3 仿真结果处理与分析

3.1 颗粒运动轨迹

颗粒运动轨迹是设计斗式提升机机罩轮廓与尺寸的主要依据，只有根据精确的颗粒运动轨迹曲线才能正确绘制机头轮廓。文献[14-15]中理论推导了卸料过程中颗粒的运动方程，但其只能间接地反映出颗粒的运动轨迹。为了更形象地得到颗粒运动轨迹轮廓线，取深斗、斗速为1.5 m/s的仿真结果进行处理，以头轮中心线(X=0，Z=0)为参考基准，得到编号为3667、 1686、 3649、 319、 3060的5个颗粒运动轨迹连接的流动域外轮廓线，如图3所示。由图可以看出，颗粒流动域外轮廓由这5个颗粒运动轨迹共同决定，以X=490 mm为界限，编号为1686、 3649的颗粒轨迹连接轮廓曲线前半段，编号为3060、 319、 3667的颗粒轨迹连接轮廓曲线后半段。Z轴方向最大卸料位移由3649号颗粒取得，约为700 mm，X轴方向最大卸料位移由3667号颗粒取得，约为1 400 mm。每个颗粒的运动轨迹在Z轴最大卸料位移处的两侧范围对称分布，这是由颗粒卸出料斗后的运动性质决定的。

图3 颗粒流动域外轮廓

取运动轨迹最接近流动域内外轮廓线的2个颗粒进行分析，得到斗速为1.5 m/s的深、浅型料斗卸料的颗粒流动域，如图4所示。由图可以看出，深斗的颗粒包络域范围较浅斗更大，且在X=800 mm附近取得最高点，超过浅斗的包络域最高点约400 mm。在X=220 mm附近，2种料斗的颗粒流动域内轮廓线开始产生偏离，此后深斗在X轴方向卸料位移更大。在X=-180 mm附近，沿外轮廓线运动的颗粒被初始卸出，深斗卸出的颗粒Z轴方向速度更大，其运动轨迹在Z轴方向的最大位移也就更大。

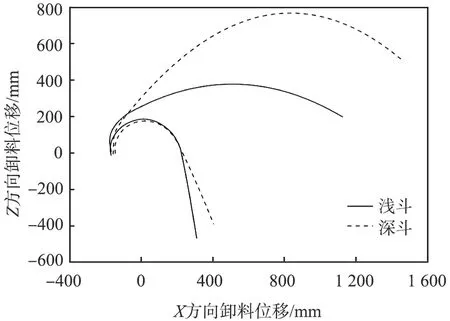
图4 颗粒流动包络域

从图3、 4可见，在机罩的结构设计上，由于颗粒在料斗内所处初始位置与所受合力不同，因此不同颗粒卸出料斗时速度不同，其运动轨迹也就不同。为了解决罩壳磨损、颗粒破碎与回流等问题，在设计机罩时应考虑其轮廓能良好引导颗粒流动，以此来改善提升机的生产性能[16-17]。

3.2 料堆表面颗粒速度分布

颗粒在料斗内的运动特性决定了其卸出料斗后的速度，从而影响卸料性能。为了探究颗粒在料斗内的运动速度分布，取料堆表面处的颗粒样本进行量化分析(斗速选为1 m/s)。图5所示为料堆表面的取样颗粒位置。为了方便统计颗粒速度信息，取样颗粒选定在运动至平行YOZ平面。取样范围为图5的矩形单元，厚度(X轴方向尺寸)为4 mm。由于颗粒半径为2 mm，因此取样厚度为4 mm就可以消除颗粒速度统计重叠与盲区的影响。

图5 料堆表面取样颗粒位置

卸料阶段卸出的主要是料堆表面的颗粒，由于该位置处物料挤压作用弱，因此颗粒流动会更容易。料斗处于绕过头轮75°位置，取样面长度为110 mm、宽度为80 mm，颗粒速度分布正视图如图6所示。这里的颗粒速度为颗粒在Z轴方向的速度，但是颗粒位置参考点以取样图所指定的为准。

料堆表面取样颗粒的速度等值线如图7所示。由图可以看出，颗粒速度最大值在Y=60 mm、Z=75 mm处取得，为0.721 m/s。在0.410 4～0.587 9 m/s速度范围内，速度等值线分层均匀。在Z=30 mm下端区域，颗粒速度基本一致，为0.410 4 m/s，该部分颗粒约占整个取样范围的37.5%。Y轴方向上，颗粒速度差别不明显。由图6可以看出，斗沿处少数几个颗粒速度较大，在Z轴方向50～70 mm区域，颗粒速度为整个速度区间中间水平，速度差值不明显。在Z=50 mm以下范围，颗粒速度差别也不大，表明颗粒运动同步性强。

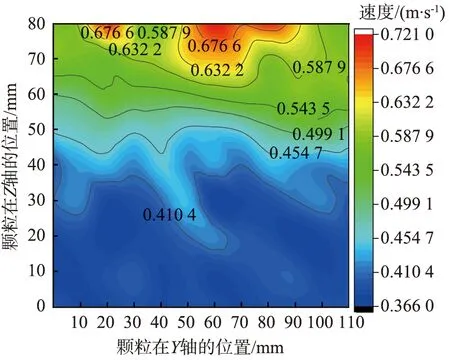
图7 料堆表面颗粒速度等值线

颗粒卸出料斗后的运动角速度越大，颗粒运动越剧烈，颗粒系统损耗的能量也越多，严重时会在罩壳内引起粉尘爆炸。图8所示为料堆表面颗粒角速度取样正视图，图9所示为料堆表面颗粒角速度在Z轴方向的分布。由图8可看出，大部分颗粒角速度较小，大致分布在33～181 r/min。在Z=50 mm以下区域，颗粒角速度明显集中，而在Z=50 mm以上区域，仅个别颗粒角速度达到峰值。由图9可以看出，在Z=20 mm处，颗粒角速度最小且分布集中，约为75 r/min。在Z=0～40 mm范围内， 颗粒角速度分布集中，但数值较小。颗粒角速度在Z=40 mm以上区域均匀增长，但分布较分散。当颗粒流向斗沿时，由于料堆表面颗粒运动会受到行程前方颗粒的阻碍作用，颗粒旋转受限，因此后端区域颗粒角速度较小。

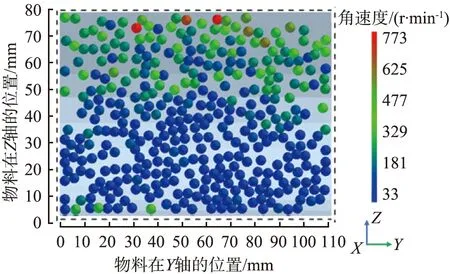
图8 料堆表面颗粒角速度分布正视图

图9 料堆表面颗粒角速度在Z轴方向的分布

3.3 颗粒流动位置分布特性

斗式提升机结构在Y轴方向具有几何对称性，为了探究颗粒流动在该方向上的位置分布特性，取斗速为1.5 m/s的浅斗卸料过程进行分析。 借助DEM软件后处理功能在Y轴方向上将颗粒流动域均分为20层，并从-Y到+Y方向依次记为1， 2，…，20，料斗绕离头轮时刻各统计层的颗粒数量如图10所示。 由图可以看出， 颗粒空间位置在统计区域上分布对称性良好。 斗速越大， 中间统计层颗粒数量越少， 表明颗粒运动沿两侧离散程度较大。 颗粒分布主要集中在7—14层， 此处也正为斗宽所在区域。 由于颗粒之间、 颗粒与料斗之间存在碰撞作用， 因此颗粒流动在Y轴方向上会离散， 若离散程度较大， 就需要考虑增加斗式提升机宽度来包络颗粒的运动。

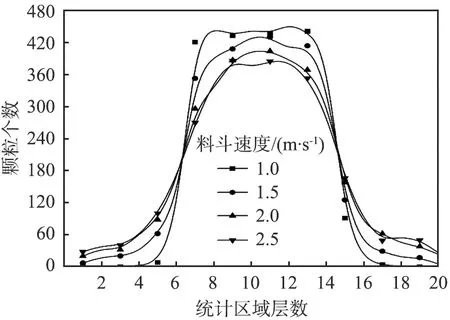
图10 不同统计层中颗粒的数量

颗粒空间位置分布对称并不能反映运动速度的一致性，为了探究颗粒速度的分布特性，本文中通过统计对称区域内相同速度的颗粒数量来进行分析。以斗式提升机对称两侧+Y、-Y层为统计区域，取速度为2 m/s的浅斗绕离头轮时刻的卸料仿真结果进行分析，得到不同统计速度时的颗粒数量，如图11所示。由图可以看出，在+Y、-Y两侧区域，不同统计速度时的颗粒数量非常一致，表明颗粒运动形态基本相同。当统计速度为4.3 m/s时，颗粒数量最多，说明该部分颗粒运动最活跃，若其与机壳发生碰撞，破碎概率最大。

3.4 颗粒流动生产率统计

颗粒流动生产率是衡量生产性能的指标之一，当颗粒尽可能多地流动到卸料槽时才能保证卸料效果良好。为了统计颗粒流动生产率，寻找最优生产参数，采用前述仿真模型对稳定流动阶段的颗粒质量流率进行统计。图12所示为统计盒子布置图，通过它来测量颗粒流过统计面的质量流率。

图11 不同统计速度时的颗粒数量

图12 颗粒质量流率统计盒子布置图

图13所示为斗速是2 m/s时不同斗型的颗粒质量流率随时间变化关系。由图可知，颗粒质量流率变化周期性良好，浅斗的质量流率较深斗的更小。深斗的颗粒质量流率波峰值可达1.9 kg/s，与波谷差值约为1 kg/s。浅斗的颗粒质量流率波峰、波谷差距不明显，平均数值约为0.8 kg/s。通过对仿真结果分析可知，浅斗的颗粒质量流率较小，原因在于颗粒卸出更早，与机顶碰撞作用剧烈，颗粒反弹后流回底槽，从而流至卸料槽的颗粒较少。

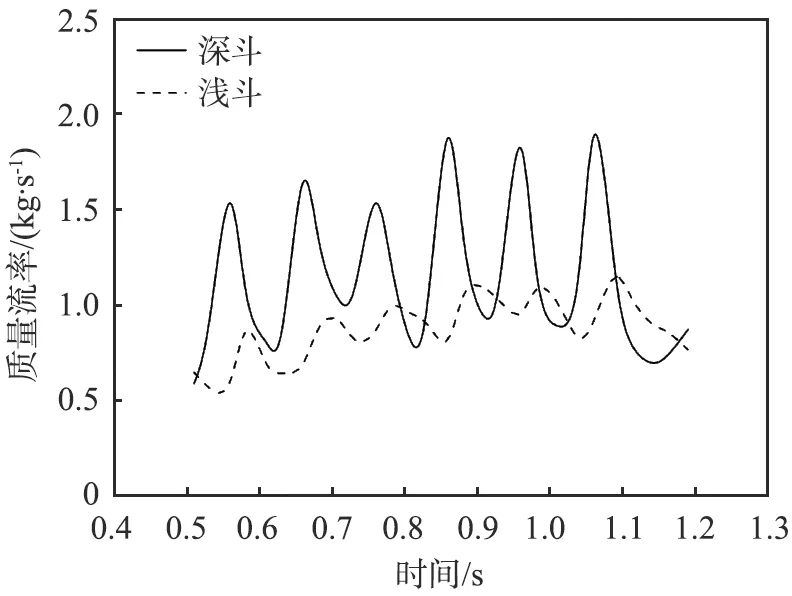
图13 不同斗型的颗粒质量流率随时间的变化

取深斗卸料进行分析，图14所示为不同斗速下颗粒质量流率随时间的变化。由图可以看出，斗速为1.5 m/s的颗粒质量流率波峰与另2组的差距不大，但波谷明显小于另2组的。斗速为2.0、 2.5 m/s时，颗粒质量流率平均水平相当，约为1.3 kg/s，但斗速为2.5 m/s的颗粒质量流率波峰、波谷差值更大。对仿真结果分析可知，3种斗速时颗粒与机顶碰撞作用适中，回流集中在部分颗粒不能流至卸料槽。虽然斗速为2.0、 2.5 m/s的颗粒流动存在形态差别，但是大多均能流至卸料槽，回流损失极少，因此平均质量流率水平相当。斗速为1.5 m/s时，由于有大部分颗粒卸出后并不能流至卸料槽，因此该部分颗粒形成回流，造成生产损失。

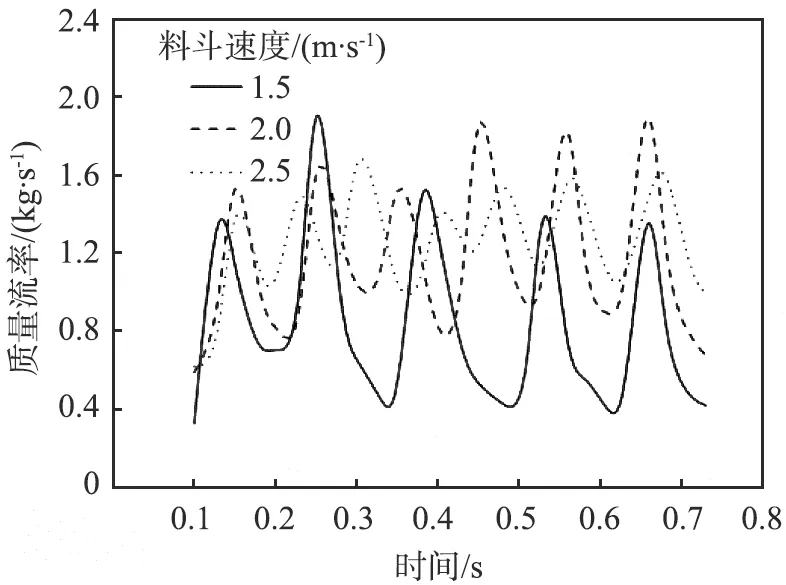
图14 不同料斗速度时颗粒质量流率随时间的变化

为了全面分析料斗在不同类型、速度时的卸料性能，以颗粒生产率(颗粒生产率为每只料斗内流至卸料槽的颗粒数量占其所装载颗粒数量的比)进行统计，测得每只料斗的卸载量如表2所示。由表可以看出：斗速为1.0 m/s的深斗颗粒生产率平均值最小，为48.75%；斗速为2.5 m/s的深斗颗粒生产率平均值最大，为95.39%。每只料斗在其他参数相同时，颗粒生产率基本一致。2种料斗随速度增大，颗粒生产率也增大，但是在2.0～2.5 m/s速度区间增幅不明显。斗速为1.0、 1.5 m/s时，浅斗的颗粒生产率较深斗的更大，但在斗速为2.0、 2.5 m/s时较深斗的小。

图15所示为不同斗速时斗式提升机内颗粒的流动形态。 由图可以看出， 在料斗速度为1.0 m/s时，虽然卸料颗粒与机顶无碰撞作用， 但是大量颗粒不能流至卸料槽， 造成平均卸载量减少， 且深斗返料较浅斗更严重。 在斗速为2.0、 2.5 m/s时， 大部分颗粒均能流至卸料槽， 因此其平均卸料量较大， 同时颗粒与机顶碰撞程度也更剧烈。 对比几组数据发现， 虽然斗速为1.5 m/s的深斗的平均卸料量比较适中， 但是颗粒与机顶碰撞作用弱， 是兼顾生产率高与颗粒与机壳碰撞作用弱的最优组合。 结果表明： 若仅追求高颗粒生产率， 则选择斗速为2.5 m/s的深斗用于卸料较好； 若追求高生产率同时又需保证颗粒与机壳碰撞作用弱， 则选择斗速为1.5 m/s的深斗用于卸料较好。

表2 不同料斗速度时每只料斗的颗粒生产率 %

图15 不同料斗速度时斗式提升机内颗粒的流动形态

4 结论

本文中分析了物料流动的运动机理，借助DEM软件对卸料过程进行了仿真模拟，研究了物料的流动轨迹与速度分布特征，统计分析了物料空间位置分布特性与流动生产率，得到以下结论：

1)卸料包络域由多个颗粒运动轨迹决定，深斗的卸料包络域较浅斗的更大。生产中选用料斗时，应按颗粒特性与机罩轮廓来考虑。

2)料堆表面上，颗粒速度分层均匀，沿Z轴正方向，颗粒速度依次增大。在Z=20 mm处，颗粒角速度最小且分布集中，随着Z轴方向高度增加，颗粒角速度线性增长。机罩设计上，采用DEM软件模拟可精确、快速认识颗粒卸载时的流动特征，利于设备的快速开发。

3)颗粒流动空间位置、速度分布在几何结构上对称性良好。在对生产过程监控时，可只在结构一侧安装信息采集设备，这样不仅能减小设备安装范围，而且能节约成本。

4)在4种斗速、 2种斗型下，若仅追求高的颗粒生产率，则选择斗速为2.5 m/s的深斗用于卸料较好；若追求高的颗粒生产率同时又需保证颗粒与机壳碰撞作用弱，则选择斗速为1.5 m/s的深斗用于卸料较好。