基于CSI相位矫正的室内指纹定位技术研究

刘兆岩，陈立伟，黄 璐

(1.哈尔滨工程大学，黑龙江 哈尔滨 150000；2.卫星导航系统与装备技术国家重点实验室，河北 石家庄050081)

0 引言

室内位置服务[1]在一些特定场合的需求日趋增强，商场、机场、医院及停车场等场合越来越意识到能够得到精准室内位置信息的好处[2]。全球导航卫星系统(GNSS)使室外定位的准确率达到了很高水平，但是在复杂的室内环境，GNSS信号衰减过大、不可靠[3]。多年来，科研机构一直努力研究，试图探索出其他技术，以获得可靠、准确的室内定位系统(IPS)。其中一些定位技术已经取得了成功，如iBeacon定位技术、射频识别(Radio Frequency Identification，RFID)技术及超宽带(Ultra Wideband，UWB)技术等[4]。iBeacon定位技术设备小、普适性强、易集成，但稳定性差、覆盖范围小。RFID技术成本低、精度高，但有着传输距离短、不易集成的弊端。UWB技术有较高的精度，但是成本较高。各种定位技术都由于精度问题或附加设备的成本问题而缩小了其潜在的应用范围。WiFi室内定位技术是为解决上述问题而迅速发展的一种室内定位技术，受到了越来越多的重视[5]。传统的WiFi室内定位技术中，接收信号强度指示(Received Signal Strength Indication，RSSI)由于成本低且容易获取而被广泛应用[6]。但因为RSSI的粗粒度以及高度易变性，在获取过程中存在信号不稳定、误差大等问题，从而无法在复杂的室内环境中实现高精度定位[7]。

近年来，随着多入多出(Multiple-Input Iultiple-Output，MIMO)系统和正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)系统在IEEE 802.11a/n标准中得到不断应用，同样可以从WiFi设备中获取信道状态信息(Channel State Information，CSI)，它代表了发射天线到接收天线的每一个子载波的信道矩阵，包含了每个子载波的幅度和相位信息[8]，可以为每个位置提供更细粒度和丰富的信息。

本文提出一种基于CSI相位差分指纹的室内定位方法，在离线阶段通过接收CSI信息，获取每个子载波矫正相位信息构建指纹数据库。在线阶段利用改进WKNN算法对实时采样信号进行在线匹配，最终完成采样点的位置估计。

1 CSI信息获取及数据预处理

1.1 CSI获取

CSI[9]在物理层表征了收发信机之间通信链路的信道特性。它不仅提供了环境衰减、距离衰减等信道信息，还反映了室内环境下信号传输存在的反射、散射和衍射等情况。在频域空间中，不同子载波的幅度和相位信息将以CSI信道矩阵的形式进行描述。在窄带平稳衰落信道中，OFDM系统的频域模型：

Y=HX+N，

(1)

式中，Y，X分别为接收信号向量和发射信号向量；H为信道矩阵；N为附加的高斯白噪声向量。信道矩阵可以完全地描述信道的特性[10]，信道矩阵可由下式估计得出：

(2)

在OFDM系统中，信号通过多个子载波进行传输，因此信道矩阵H可以表示为：

H=[H1,H2,…,HN]，

(3)

式中，Hi为第i个子载波上的CSI，可以表示为：

Hi=|Hi|e-i∠Hi，

(4)

式中，|Hi|，∠Hi分别为第i个子载波上的CSI幅值和相位。应用在IEEE 802.11n标准[11]的MIMO系统中支持多输入天线和多发射天线，因此CSI矩阵可以表示为：

(5)

式中，t为发射天线数；r为接收天线数。

本文将使用配有Intel 5300无线网卡的电脑，在Ubuntu 12.04 LTS-Ubuntu 14.04 LTS 系统下，通过修改无线网卡的驱动，利用Linux系统中的系统函数将CSI信息导出为.dat格式的文件。

1.2 数据预处理

CSI因其丰富的数据特征而被作为指纹用于室内定位研究当中，但由于硬件条件的影响，接收机和发射机之间的同步误差不能完全消除，往往接收机接收到的CSI中包含时钟同步误差以及不同载频误差引起的相位偏移。发生偏移的原始相位信息错综复杂，因此很少会将相位信息作为指纹。30个数据包的原始相位如图1所示。

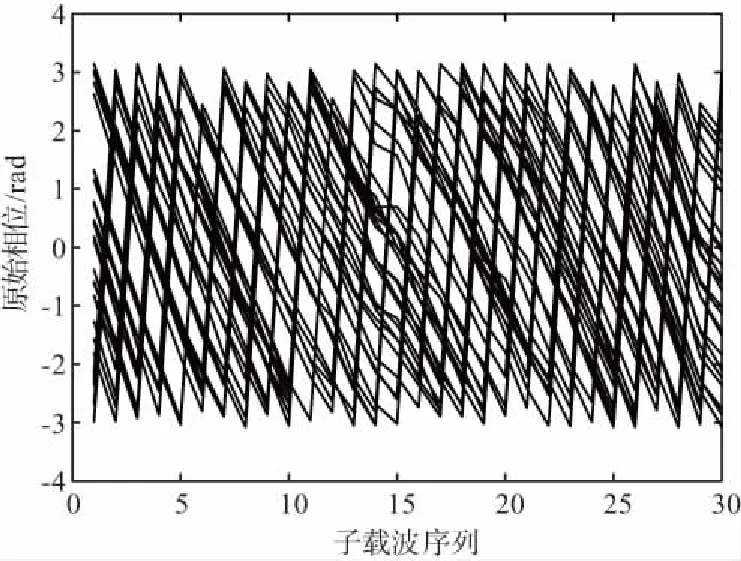
图1 30个数据包的原始相位Fig.1 The original phase of 30 packets

针对上述问题，本文采用基于线性变换[12]的方法对原始相位进行预处理，消除不同载频误差引起的相位偏移，得到CSI真实相位。

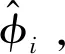
(6)

式中，φi为第i个子载波的真实相位；mi为第i个子载波的索引号；N为快速傅里叶变换的大小；Δt为接收端时间偏差；β为由载频误差引起的相位偏移；Z为测量噪声。为了将未知的Δt，β剔除，得到真实相位值，引入2个中间量k，b，定义如下：

(7)

(8)

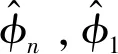
(9)

原始相位经过线性变换后，相位中不再包含时间偏差Δt和相位偏移β，图2给出了在同一位置用2根接收天线接收的原始相位及通过线性变换得到真实相位。

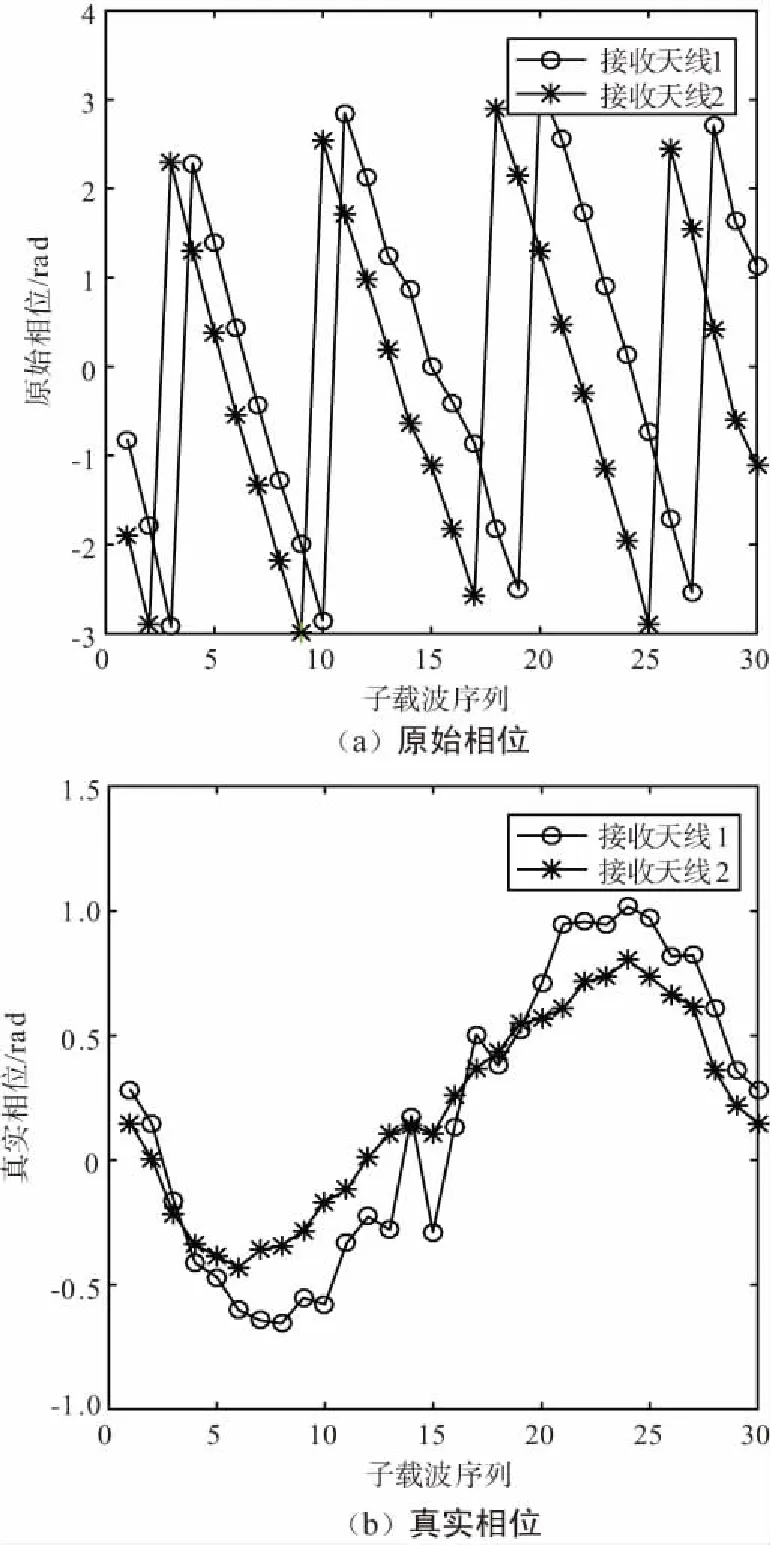
图2 原始相位及真实相位Fig.2 Original phase and true phase

由图2可以看出，经过线性变换得到的CSI相位仅仅是真实相位的线性组合，规律性更加明显。

图3是在3个不同位置用同一根天线采集30个连续数据包的真实相位图。由图3可以看出，经过线性变换得到的真实相位在同一点基本稳定，而且不同点区分度明显，有利于将CSI相位信息作为指纹进行定位。

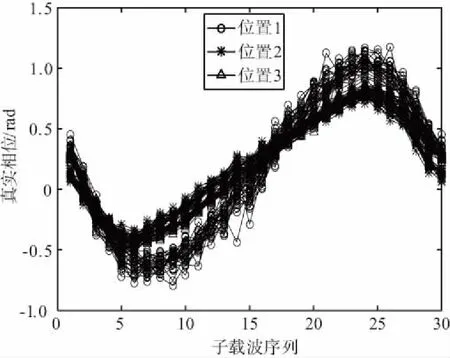
图3 3个位置点的30个数据包的真实相位Fig.3 The true phase of 30 packets at three locations

2 基于指纹库匹配的室内定位方法

基于指纹库的CSI定位技术是利用接收天线采集信道的状态信息，建立信号特征值参数指纹库。将待定位点采集到的特征值参数与指纹库中特征值参数进行匹配计算，从而得到待测点的实际位置。指纹库定位技术分为2个阶段：离线建库阶段和在线定位阶段[13]。

2.1 离线建库阶段

离线建库阶段主要包括采集WiFi CSI信息，对采集信息进行预处理，提取矫正后的相位信息，建立特征值指纹库。建立特征值指纹库首先在测试区域内选定m个测试参考点，然后依次采集每个测试参考点的特征值参数Fmn，每个点的特征值(Fm1,Fm2,…,Fmn)对应该点坐标(xm,ym)，按如表1的格式存储在数据库中。该数据库即为特征指纹数据库。

表1 指纹库格式
Tab.1 Fingerprint database format

x1y1F11F12…F1nx2y2F21F22…F2n︙︙︙︙⋱︙xmymFm1Fm2…Fmn

其中，(xm,ym)为测试参考点m的坐标；(Fm1,Fm2,…,Fmn)为测试参考点m的n维特征值参数。

2.2 在线定位阶段

在线定位阶段，对比计算待定位点的数据特征值与指纹库中的特征值，在指纹库中匹配得到一组最近的特征值参数，得到相应的位置坐标，完成设备或人员的定位。定位流程如图4所示。

图4 指纹定位流程Fig.4 Fingerprint positioning flowchart

2.3 改进WKNN算法

KNN算法[14]只是选取距离最近的k个近邻参考点而忽略了它们的距离差别，当指纹数据库分布不均时，待定位点与近邻参考点距离差别较大，会影响定位精度。因此，本文提出的一种改进的WKNN算法，该算法在传统WKNN算法初次得出位置坐标的基础上进行二次匹配，计算得出最终坐标。

传统的KNN算法首先计算待定位点特征值组(F1,F2,…,Fn)到指纹数据库参考特征值组之间的距离，本文采用欧氏距离，具体计算如下：

(10)

式中，Li为待定位点与指纹数据库中第i个参考点的欧式距离；Fj为待定位点特征值组中的第j维特征值；Fij为特征值指纹数据库中第i个参考点的第j维特征值，i=1,2,…,m;j=1,2，…,n。

然后在Li中选取距离由近到远的k(k≥2)个参考点，则待定位点的位置坐标可由这k个参考点估算得出：

(11)

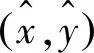
本文采用的改进WKNN算法为每个近邻参考点坐标分配一个权重，权重由待定位点和近邻参考点的距离Li经高斯函数变换得到：

(12)

式中，Wki为k个近邻参考点中第i个点的权重；Lki为待定位点到k个近邻参考点中第i个点的距离；Limin为待定位点到k个近邻参考点中第i个点的最小距离；a为最大权重值，通常取1；b为半峰宽度，可根据k值调整。

之后，为每个紧邻参考点加上对应权重，即可由WKNN算法得到定位坐标：

(13)

考虑到真实坐标与距离最近的k个紧邻点关联性较强，本文提出一种二次匹配定位算法，该方法在初次匹配得到定位坐标的基础上，首先计算初次定位坐标与k个紧邻点的欧氏距离Ldi，将k个距离值经过高斯函数变换得到各自的权重，改进后的计算公式：

(14)

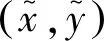
完整的改进WKNN算法定位步骤如下：

① 首先在地面设置参考点，采集所有参考点的CSI信息，并经过数据预处理建立特征值指纹数据库；

② 在线采集待定位点CSI信息，经过预处理与指纹数据库匹配计算得到k个紧邻参考点；

③ 计算k个紧邻参考点对应的权重；

④ 由k个紧邻参考点的加权坐标得到待定位点的初次预测坐标；

⑤ 计算初次预测坐标与k个紧邻参考点的欧式距离，并经过高斯变换得到二次权重；

⑥ 给k个紧邻参考点分配对应的二次权重，预测最终位置坐标。

3 实验测试结果

为验证本文所提算法的可行性和有效性，搭建了WiFi指纹定位平台。选取厂房作为测试环境，选取测试范围为5 m*5 m。厂房可以模拟大型体育场馆、机场和火车站的空旷环境，为实现高精度室内定位，本文使用3个AP，AP布设及测试区域平面图如图5所示。其中AP布设位置为图5中黑点。

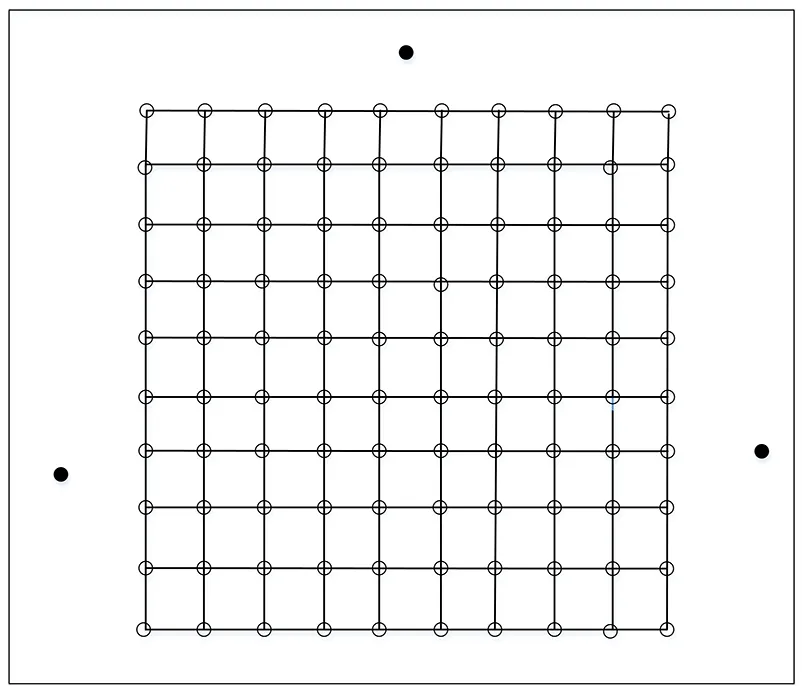
图5 测试环境平面图Fig.5 Test environment plan

3.1 离线构建指纹库

首先设置等间距的参考点，如图5白点，参考点数为100个。在测试区域建立直角平面坐标系，标定每个参考点的位置坐标。采集参考点数据，提取数据中的CSI相位信息，并进行预处理，处理后的数据与之对应的坐标按表1的格式保存，得到离线的特征值指纹数据库。

3.2 在线定位

测试人员选取5个测试点进行定位测试，在线采集待测试点数据时，室内其他活动正常进行。对采集到的数据进行预处理，得到待定位点的特征值参数，每个点任意选取10组特征值参数进行定位分析。

3.3 定位结果及分析

本文所采用的定位算法k值的选取会影响定位结果[15]。为获得最优定位结果，选取了不同的k值进行定位分析。图6给出了WKNN和改进WKNN2种算法在相同指纹数据库、相同待测试点的情况下，不同k值所得到的平均定位误差。

图6 2种算法不同k值平均误差Fig.6 Different k-valued average error plots for the two algorithms

横轴k值，分别选取3,4,5,6,7,8,9,10，纵轴为5个待测试点的平均定位误差。由图6可以看出，改进WKNN的平均定位误差都低于WKNN的平均定位误差。在使用WKNN时，k值选取4,5,6,7,8的定位误差差别不大；k为3时，定位误差最小；k为7,8,9,10时，随着k值的增大，定位误差逐渐增大。在使用改进WKNN算法时，k=3时，平均误差最小；其他k值时，平均定位误差比较稳定。根据图6的结果，确定k=3。

图7和图8是在k取3时，分别使用传统WKNN算法和改进的WKNN算法进行定位所得到的误差对比图和误差累计分布函数图。

图7 2种定位算法误差对比Fig.7 Comparison of two positioning algorithm errors

图8 2种定位算法误差累计分布函数图Fig.8 Error distribution function diagram of two positioning algorithms

可以看出，使用传统WKNN算法进行定位，定位误差在1 m以内的概率为80%左右，最大定位误差超过了1 m。而使用本文所提出的改进的WKNN算法后，所有定位点的误差均优于1 m，并且相较于传统WKNN算法定位不存在定位偏差较大的点，增加了定位系统的稳定性。表2给出了具体的定位误差数据。

表2 数据处理前后定位精度对比

Tab.2 Comparison of positioning accuracy before and

由表2可以看出，使用改进WKNN算法的定位结果在平均误差、最大误差方面都优于传统WKNN算法的定位结果。在最小误差方面，传统WKNN算法跟改进WKNN算法定位误差相当，这是因为数据中存在一部分特征值，这部分正常值的定位精度较高，决定了最小误差的下限。经过实验验证，改进的WKNN算法可以有效提高定位精度，有效减小信号波动带来的影响，最大定位误差仅为0.98 m，可满足室内定位需求。

4 结束语

本文提出一种基于CSI相位指纹匹配的室内定位方法，在离线建立指纹库阶段增加了对测量CSI相位预处理的过程，提高了指纹数据库的可信度。在此基础上提出了改进加权K近邻法对在线采集到的信号进行匹配定位。通过实验验证，所提算法可以有效提升定位精度，平均误差达到0.63 m，基本可满足室内定位需求。但指纹数据库采集工作量大，在保证定位精度的同时如何减少工作量将是下一步研究的重点。