基于伪卫星的室内定位算法研究
于雪岗,封 欣,邓志鑫
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.中国人民解放军32021部队,北京 100094)
0 引言
室内定位[1]是当前定位导航领域的一个重要方向,有着各种各样的应用场景,例如商场内商家精确导航、室内位置共享等模式。为了实现室内定位,目前开发了多种定位手段,包括蓝牙定位、WLAN定位[2]、视觉定位、激光定位和惯导定位等多种定位手段,但这几种定位手段均存在定位精度差的问题。对室外定位来说,GNSS系统[3]目前已经能够满足cm级定位需求,利用这一系统原理建造相似的室内定位系统来满足人们的定位需求,开展室内伪卫星系统定位算法研究,开展使用伪卫星进行室内定位的理论可能性及工程实现,并在当前已有的接收机基础上进行算法分析及改进,分析伪卫星室内定位中存在的问题及优缺点。
1 室内伪卫星模型
鉴于室内环境布设场地有限,伪卫星布设可以采用阵列的形式来实现,以减小系统设计的空间需求,这样会产生空间位置精度因子(PDOP)[4]恶化的后果。PDOP只与伪卫星布设和用户位置有关,与其他因素无关。假设用户坐标位置为P=(x,y,z),伪卫星坐标位置为Pn=(xn,yn,zn),由此可以得出几何矩阵:
(1)
权系矩阵H:
(2)
PDOP为:
(3)
在较为空旷的室内环境中,伪卫星阵元可以悬挂在室内上空,采用八阵元的形式,阵元间隔约为1.3 m,采用七围一的形式,其结构图和PDOP分布如图1所示。
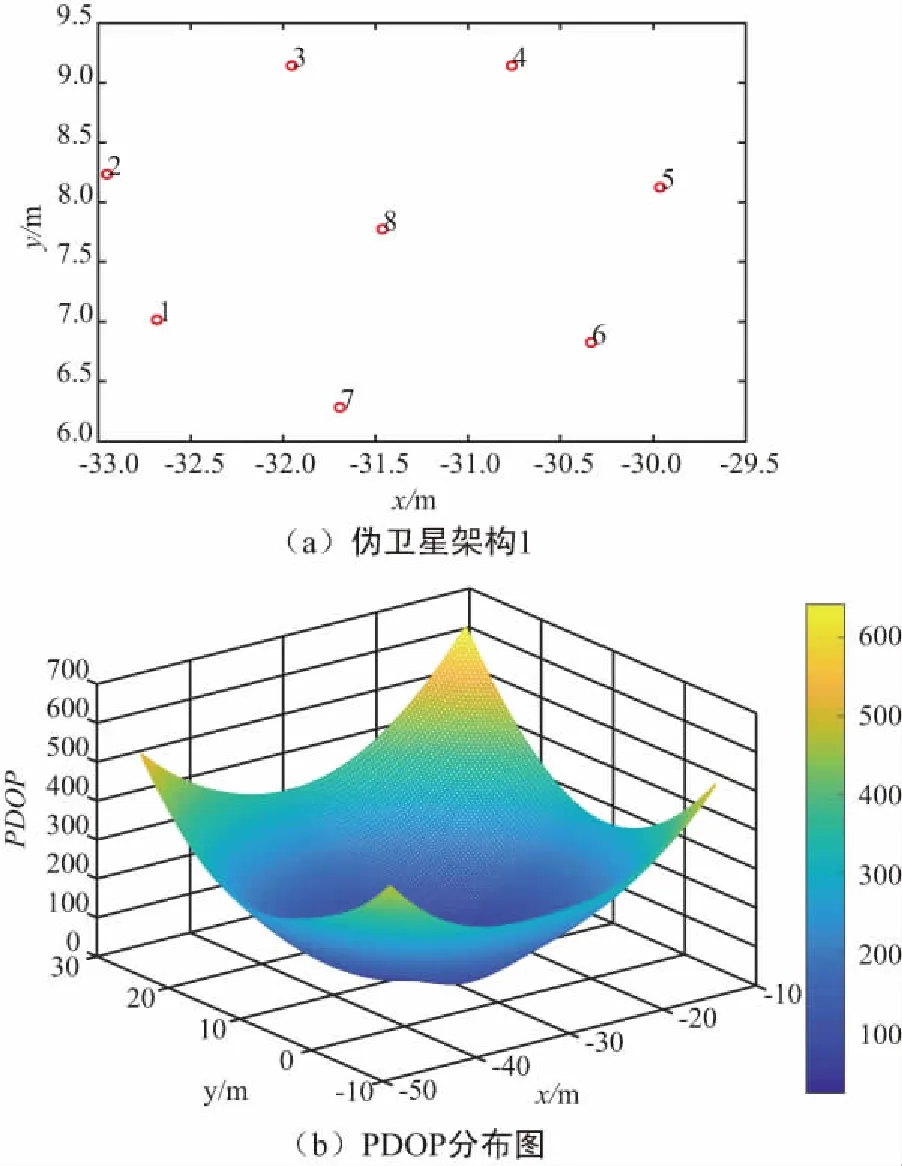
图1 伪卫星架构1及PDOP分布示意Fig.1 Pseudo_satellite architecture 1 and PDOP distribution diagram
室内环境如果存在狭长的走廊时,伪卫星阵元只能在走廊一侧倾斜安装,阵元间隔约为1.1 m,其结构图和PDOP分布如图2所示。

图2 伪卫星架构2及PDOP分布示意Fig.2 Pseudo_satellite architecture 2 and PDOP distribution diagram
对卫星导航系统来说,为保证定位精度和最小二乘定位算法[5]收敛性,PDOP一般要求小于99,室内环境中大部分区域都不满足这一特性,引起定位误差大甚至使用最小二乘定位算法时,定位不收敛的情况。
室内定位中存在的另一个问题在于室内环境复杂,用户机除了接收到伪卫星直射波以外,还会接收到该直射波多份反射波的斜波,这种反射波对接收机性能的影响成为多路径效应[6]。假设信号为s(t),直射信号为A*p(t)*sin(2*pi*f*t),则存在:
s(t)=A*p(t)*sin(2*pi*f*t)+
(4)
接收信号与本地伪码相干积分后自相关函数[7]表示为:
(5)
反射波的相位φi具有随机性,其与直射波的相位关系具有不确定性。由于室内环境相比室外环境[8-9]更为复杂,多路径效应也更加显著,出现二次反射波或者多次反射波,严重影响自相关函数特性[10-11],降低码相位和载波相位精度,进而影响伪距测量精度,降低接收机用户定位和定速精度。由于载波相位测量值相位[12]误差最大不超过90°,即1/4波长,误差为cm级,所以在一定条件下通过载波相位平滑伪距对伪距测量精度有较大的提升作用。在室内环境下对伪距测量值和载波相位平滑伪距值进行测试,其实测结果如图3所示。

图3 伪距测量误差和载波相位误差示意Fig.3 Pseudo-measurement error curve and carrier phase measurement error curve
由图3可以看出,相对于伪距直接测量,多路径效应对载波相位测量值的影响会更小,所以采用载波相位平滑伪距的方式可以减少伪距测量值中的多路径误差,同时在接收机中可以通过窄相关处理,多路径消除等技术手段减少多路径效应对接收机的影响。
2 遍历算法
从上述分析可以得出,室内环境存在伪距测量精度低、几何位置精度因子差的特点,这2种因素会造成最小二乘定位算法发散不收敛,所以这种传统的定位算法不再适合于室内定位。同时,室内环境存在用户动态低、高程变化慢的特点,结合这些特点,为了实现室内伪卫星定位功能,开发了一种新的室内定位算法——遍历定位算法,新算法具有稳定性强,对伪距测量精度要求低的特点。遍历定位算法主要依据载波相位平滑伪距,在上一个定位点的一定范围内平面搜索最符合伪距变化规律的位置作为新的定位点,这就要求在室内环境中存在一个基准点位置作为遍历定位算法的初始值,而室内环境很容易能够满足这一要求。遍历定位算法的流程如图4所示。

图4 遍历定位算法流程示意Fig.4 Traversal localization algorithm flow diagram
图4中Δx,Δy分别为平面垂直两方向搜索步长,决定了搜索精度;M,N为步进次数,决定了平面搜索范围。
通过载波相位得到一组伪距测量值R,通过假设位置点估计另外一组伪距估计值Rt1,通过这2组伪距值计算评估值来评估当前位置是否为最优位置。伪卫星位置为Pn,上时刻伪卫星位置为Pt0=(x,y,z),下一时刻假设位置为Pt1=(x+Δx*i,y+Δy*j,z),则有:
(6)
E=R-Rt1,
(7)
式中,E为伪距测量值和伪距估计值之间的误差向量。实际工程中,接收机和伪卫星中都存在钟差等一系列共性误差,为了消除这些误差对评估值的影响,根据误差具有共性的特点,对误差向量E取单差,改进后的误差向量为:
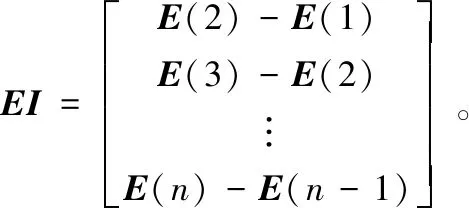
(8)
误差向量EI表示假设位置点伪距估计值和实际的伪距测量值之间的误差,其模值越小则和实际坐标点越匹配,在合理范围内搜索出的最小模值点即为下一时刻的坐标定位点。坐标点误差分布曲线和投影曲线如图5所示。

图5 遍历误差分布曲线及投影曲线示意Fig.5 The error distribution curve and projective curve
3 遍历算法定位结果
相对于最小二乘算法,遍历算法需要占用更多的资源,而且随着搜索精度和范围的提高,搜索所需时间将几何增长,极大限制了遍历算法在室内定位中的工程实现。为了满足室内定位工程需求,需要对遍历算法搜索范围和精度进行合理分配,在硬件限制范围内实现不同精度要求。通过工程测试,其定位效果如图6(b)所示。

图6 遍历算法收敛曲线和定位效果Fig.6 The convergence curve of the traversal algorithm and positioning effect chart
图6(b)中直线为规划路线,黑色为遍历算法定位曲线。实验证明,遍历算法定位曲线和实际规划路线基本重合,定位误差在0.3 m以内,并且能够最终在起始点闭合,满足室内定位精度需求。
4 结束语
目前,室内定位实现手段众多,为了满足室内定位需求,采用多元融合的形式进行定位实现。伪卫星室内定位具有精度高、易实现的优点,是当前室内定位的一个重要手段,有很大的发展前景。同时,伪卫星室内定位也存在各种各样的问题有待解决,尤其是多路径效应和高程计算问题。

