基于多方向的各向异性边缘检测算法

王益艳

（1.四川文理学院智能制造学院 达州 635000）（2.达州智能制造产业技术研究院 达州 635000）

1 引言

边缘是数字图像最基本的特征之一，对于一幅图像来说，其大量信息是由它的轮廓边缘提供的［1］。因此，边缘检测是特征提取和纹理分析的基础，在细胞分类、CT成像、车辆牌照识别、指纹提取等领域具有重要的研究价值。图像的边缘是指图像中周围像素灰度有变化的那些像素的集合。常见的边缘点主要有两种，一种是阶跃状边缘，另一种是屋顶状边缘。阶跃状边缘处于图像中两个具有不同灰度值的相邻区域间，屋顶状的边缘上升沿和下降沿都比较缓慢。因此，可以利用图像的一阶导致的极值或二阶导数的过零点信息来提取边缘。传统的一阶边缘检测算法有Roberts、Sobel、Prewitt、Krisch等［2］，二阶边缘检测算法包括Laplacian、Log、Canny等［3～4］。这些基于导数的检测算法对噪声比较敏感，常常会在检测边缘的同时加强噪声。小波变换具有良好的局域化特性，它是检测边缘很好的工具，可实现多尺度边缘特征提取［5～6］。但是，在受噪声感染的状况下，该方法对边缘检测效果不理想。近年来，基于数学形态学的方法被广泛应用于图像边缘检测［7～9］，该方法检测出的图像边缘比传统方法具有更好的连续性和方向性［10～11］。然而，传统数学形态学检测算法主要根据形态学梯度信息提取边缘，由于没有考虑边缘的方向，导致图像出现边缘多像素宽。为此，人们提出了各种改进的多尺度形态学边缘检测算法［12～15］，在一定程度上提高了边缘检测效果，但该类方法中结构元素的选取对最终检测结果影响比较大，同时，对噪声的抑制能力也有待进一步提高。鉴于以上不足，本文提出了一种多方向的各向异性边缘检测算法。首先构造了4个具有各向异性的5阶差分模板，并对其进行归一化处理，然后分别对待检测图像进行卷积处理，根据各方向上卷积结果的幅值和方向信息提取边缘图像，最后采用最大类间方差法进行边缘二值化。大量仿真实验结果表明，该方法具有较好的边缘提取性能，比传统canny、小波变换、多尺度形态学等方法具有更高的检测精度和更强的噪声鲁棒性。

2 多方向各向异性边缘检测算法

传统基于一阶或二阶导数的边缘检测算法是利用像素上、下、左、右邻域的灰度加权差，根据在边缘点处达到极值这一原理进行边缘检测的。通常只考虑了水平和垂直两个方向。本文利用方向差分运算与局部平均相结合的原理，设计了一种新的各向异性边缘检测模板。其模板大小为5阶矩阵形式，在原有基础上增加了两个对角线方向上的检测。新模板检测算法如图1所示。

图1 5阶各向异性边缘检测模板

其中，ωτ(τ=1，2，3，4)为归一化因子。

设原始灰度图像为x(i，j)，将它与图1中四个检测模板依次进行卷积，结果分别为 y1(i，j)，y2(i，j)，y3(i，j)，y4(i，j)。其中 yσ(i，j)=xσ(i，j)Wσ，(σ=1，2，3，4)。定义梯度幅度Y(i，j)如下：

其中，k1，k2∈{1，2，3，4}且 k1≠k2，θ^edge为梯度方向。

该检测算法现实了5阶邻域内8方向的各向异性边缘检测，因此可以获得比传统方法性能更佳的全方位响应，与真实的梯度值误差更小。同时，为避免检测结果绝对值超过255，引起数据发生溢出。本文引入 ωτ(τ=1，2，3，4)作为归一化因子，其中，ω1=ω2=1 14，ω3=ω4=1 15。这样最终得到是不失真的边缘图，保留了图中所有边缘的信息。为了实现边缘二值化，本算法采用以下步骤进行处理：

1）将原始图像采用图1中的4个各向异性5阶模板进行卷积运算。

2）根据式（1）、式（2）对图像进行边缘检测，得到灰度边缘图。

3）采用基于最大类间方差的Otsu法确定二值化阈值，对灰度边缘图像进行二值化，得到最终的二值边缘图像。

3 实验结果及分析

为对本文算法进行有效验证，本文进行了多组对比仿真实验。采用如下边缘信噪比（ESNR）［13］进行客观评价：

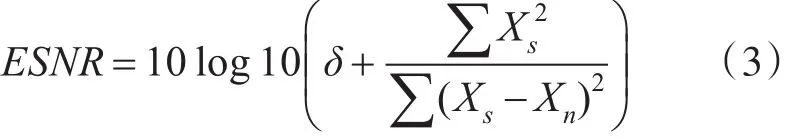
上式中，Xs表示无噪边缘图像，Xn表示有噪边缘图像。δ为常数（δ＞0，实验中取值为1）。ESNR越大，表示边缘检测精度越高。

本文采用标准的“peppers”作为测试对象，以Matlab R2011a为测试平台，计算机配置为Windows7系统、AMD A8处理器、主频1.60GHz、4G内存。将本文方法与传统canny算法［4］、小波变换［5］、多尺度形态学［8］等方法进行实验比较。图2～4给出了边缘检测视觉效果，图5～6给出了不同噪声条件下，各边缘检测方法对应的性能指标ESNR值的变化曲线。

图2 无噪声时图像边缘检测结果

图3 添加脉冲噪声时图像边缘检测结果

图4 添加高斯噪声时图像边缘检测结果

图5 各方法对应的ESNR值随脉冲噪声变化的曲线

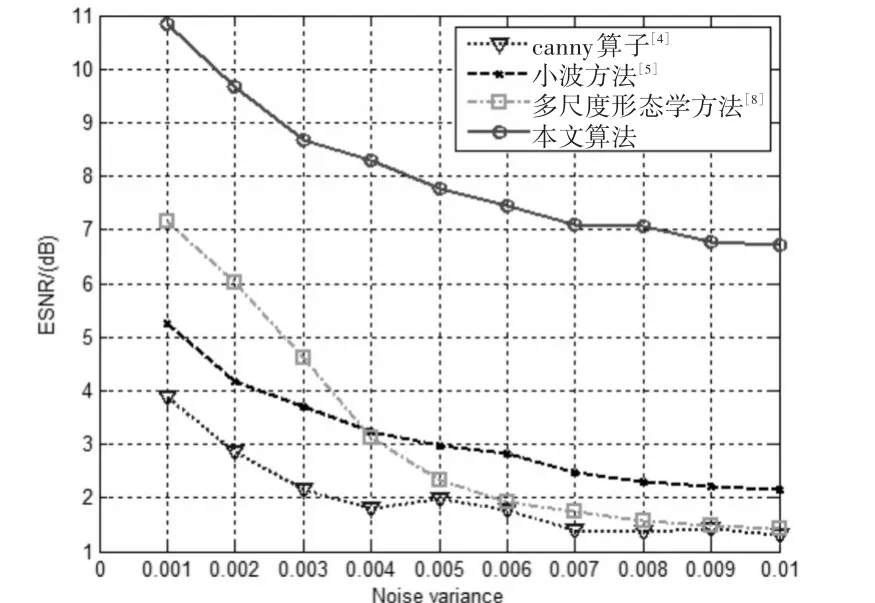
图6 各方法对应的ESNR值随高斯噪声变化的曲线

图2 结果显示，当原始图像没被噪声感染时，canny算法和小波方法存在明显的伪边缘和边缘断裂现象，而本文方法和多尺度形态学方法检测的边缘效果较好。而从图3和图4看出，本文方法对脉冲噪声和高斯噪声都具有较好的鲁棒性，检测出的图像边缘清晰可见。而其他三种方法对噪声很敏感，边缘检测结果中残留了大量噪声点，视觉效果很差。同时，从图5看出，本文方法对低密度脉冲噪声有很好的抑制效果，不过随着噪声强度增加，其性能有一定的下降。而其他三种方法对脉冲噪声抗噪性能很差。从图6看出，canny算法和小波方法对高斯噪声抗噪性能较差，多尺度形态学方法对方差较小的高斯噪声具有一定的抑制作用，但随着噪声强度增加，其噪声抑制性能下降很快，而本文方法变化趋势则相对比较平缓。因此，无论从边缘检测的主观视觉效果，还是客观评价指标来看，本文方法比另外三种方法都具有更强的抗噪性和更高的边缘检测精度。

4 结语

为了克服传统边缘检测算法抗噪性差的不足，提出了一种多方向的各向异性边缘检测算法。利用方向差分运算与局部平均相结合的原理，设计了4个具有各向异性的5阶差分模板，将各模板归一化处理后，分别对待检测图像进行卷积处理，根据检测算法在各方向上卷积结果的幅值和方向信息得到灰度边缘图，采用最大类间方差法确定阈值进行边缘二值化。最后通过多组对比实验结果，论证了本文方法的有效性和优越性。