基于改进多目标粒子群算法的DG选址定容优化研究*

陈浩 马平

（青岛大学电气工程学院 青岛 266071）

1 引言

由于分布式电源的并入，使其处于一个从传统的放射性无源网络向含源电力网过渡的时代，当然，这种变化也同时对配电网产生了全方位的影响。文献［1］应用多个算例验证了单个分布式电源在不同接入位置和接入容量的情况下对电压分布影响极大。文献［2］提出利用灵敏度分析方法研究DG不同出力对系统电压造成的影响。文献［3］从分布式电源接入个数、接入位置和容量等方面研究DG并网后对电压分布的影响规律。由于DG接入位置和容量对配电网有重要影响，对DG的选址定容研究显得意义重大。

（DG）选址定容问题是在满足给定的投资及系统运行等约束条件下，对DG的布点和容量进行优化，使得效益最大化。随着对电力系统运行要求的提高，DG选址定容问题已经从仅考虑网损最小的单目标问题［4］发展成为综合考虑电压质量、电流质量和环境因素等各个方面的多目标优化问题［5］。二次规划法［6］、遗传算法［7］等方法被应用于求解多目标选址定容问题，但这类方法需要设置权重来将多目标问题转化为单目标问题进行求解，而在现实中这些权重往往是难以确定的。针对这些缺陷，文中采用基于小生境共享机制对多目标粒子群优化算法进行改进，创新性的应用于多目标函数下的分布式电源选址定容。

本文构建了静态电压稳定指标，设置了不同的方案进行仿真，仿真结果证明了DG容量和接入位置对配网有重要影响。然后，为减少DG的容量和位置不合理规划造成不利影响，文中建立了以综合成本、网损和电压稳定裕度为目标函数的模型，采用基于小生境的改进多目标粒子群优化算法对模型进行求解，获取了DG的多目标最优Pareto解，为选址定容方决策提供依据。

2 构建静态电压稳定度指标模型

为研究分析分布式电源接入对配电网电压稳定性的影响，文中基于潮流解存在的理论构建了静态电压稳定指标。从数学的观点来看即其潮流方程或者潮流扩展方程有解则电压稳定，若无可行解则电压失稳。

简单两节点系统如图1所示。

图1 中Pj表示节点j本身的有功功率与该节点之后的所有负荷节点的有功功率和该节点之后所有支路的有功损耗之和；Qj表示节点j本身的无功功率与该节点之后的所有负荷节点的无功功率和该节点之后所有支路的无功损耗之和。根据潮流解存在理论构建的静态电压稳定指标L如下式：

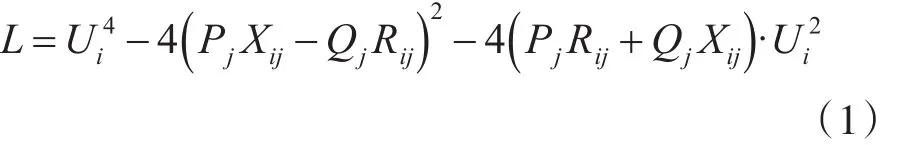
式中：Ui表示系统中节点i的节点电压；Xij表示节点i和 j之间的电抗；Rij表示节点i和 j之间的电阻。

从式（1）可以看出，满足L≥0则所对应的节点电压才算稳定，通过L值的大小可以判断电压的稳定水平，L越小，越接近于0，说明该点的电压稳定水平越低，L最小的点即是电压最可能发生崩溃的点。据此我们根据上述方法求出每个节点的L值，并对L值比较小的节点采取相应的措施避免发生电压崩溃。

3 DG优化配置目标函数及约束条件

分布式电源接入配电网的位置和容量大小的不同，都会对配电网产生多方面的影响。为此本文建立以综合成本、网损和电压稳定裕度为目标的数学模型，对DG的选址定容展开研究。

3.1 目标函数

3.1.1 综合成本

DG的综合成本主要由分布式电源的投资成本和运行成本用组成。其数学模型如下：

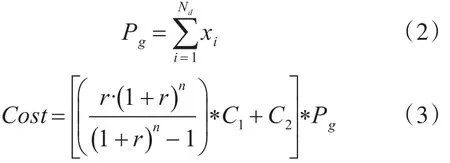
上两式中：Cost为DG投资的综合成本；Pg为DG接入的有功容量；r为贴现率；n为项目投资回收周期年限；Nd为接入DG的节点数；Xi为i节点DG的接入状态。

3.1.2 网损

配电网网损计算模型如下：

式中：Ploss为总的有功网损；l为网络支路数；Rk为第k条支路的电阻值；Ik为流过第k条支路的电流。

3.1.3 电压稳定裕度

DG接入配电网后，系统节点电压发生改变。在高峰负荷时，在节点电压较低的点接入DG，可以有效改善节点电压水平，但接入DG容量过大时，过大的电压不符合用户期望值。因此，构建电压稳定裕度指标作为分布式电源的选址定容的目标函数。其表达式如下：

式中：Ue为节点电压的期望值；Uload为负荷节点的电压值；Up为电压允许偏差；N为配网节点数目；dU为电压稳定裕度。

3.2 约束条件

1）为满足配电网必须开环运行，网络拓扑结构需满足辐射状［9］：

式中：gk为当前配电网运行结构；Gk为配电网所有辐射状结构的集合。

2）为保证配电网安全可靠运行，支路电流需满足容量约束：

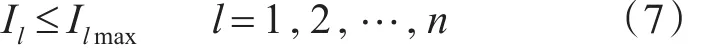
式中：Il为流过线路Ilmax的电流；Ilmax为流过线路l的最大电流；Uimin≤Ui·t≤Uimax为线路数量。

3）为满足配电网安全可靠运行，避免节点电压越限，节点电压需满足如下约束：

式中：Umin和Umax分别为节点电压的下限和上限；Ui为节点i在电压幅值，n为节点数量。4）节点分布式电源安装容量约束

式中：Nd为可接入DG的节点数目；PDGi为节点i接入DG的有功容量；为节点接入DG的最大有功容量。

5）为使配电网在任何时刻都满足功率平衡需满足如下约束条件：

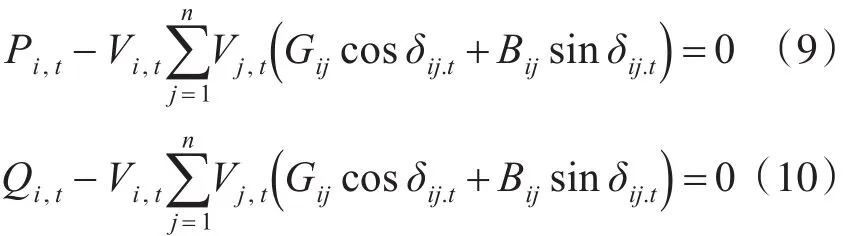
式中：Qi，t、Pi，t分别代表在时段 t注入节点 i的无功和有功；Gij、Bij、δij.t分别表示两节点i和 j间的电导、电纳和在时段t电压相角差；n为系统节点数目；Vi，t、Vj，t分别为节点 i和 j在时段 t的电压幅值。

4 分布式电源选址和定容模型求解

4.1 基本粒子群算法

BPSO是在1997年两位博士解决离散变量的寻优问题时提出的［9］。求解过程是先对种群规模个粒子随机初始化，其中第i个粒子用xi，vi分别表示其位置向量和速度向量，维数为d维，然后求出目标函数值，对粒子位置，速度向量更新，是否达到迭代次数判断输出。粒子速度和位置的更新方程［15］为

分别为粒子i在第k次迭代时的第d维速度和位置；ω为惯性权重系数；c1、c2为加速系数，分别调节向全局最优粒子和个体最优粒子方向飞行的步长；r1、r2为［0，1］之间的随机数；pid为粒子 i第d维个体最优点的位置；gd整个群在第d维全局最优点的位置。粒子i的位置取值为0或1，速度越大表示位置取值为1的概率越大。

4.2 改进多目标粒子群算法

当选择较大的惯性权重时，粒子群算法通常因为粒子偏离全局最优位置和自己的历史最优位置而具有较好的全局搜索能力，较小的惯性权重就不利于全局搜索。

2012年11月20日，落马官员雷政富的一段不雅视频在网上流传，引发了网民的热议。许多网民对雷政富的贪腐行为表达了强烈不满。但值得玩味的是，网民参与该事件的方式却是娱乐化的。如2013年6月20日，一位名为“燃烧的火炬”的网友在凯迪社区发表了一篇《2013年感动中国人物——雷政富》的帖子。作者模仿《感动中国》栏目颁奖词的结构，在帖子中将雷政富描写成“一个重情义、敢担当的中国男人，狱中一别，他让整个中国刮目相看！”[2]该帖一经发布就被大量转发和关注，许多网民纷纷跟帖，诸如“雷哥，好样的！”、“中国二个够男人的男人，雷政富，赖昌星”等娱乐性回复充斥着网络。

在可行解空间中随机初始化粒子群，选取非劣解“粒子”构成精英集P，精英集在粒子更新的过程中可以指导粒子的“飞行”。通过小生境技术求解精英集中粒子的适应度，粒子的聚集程度越高，粒子的适应度就越小。第i个粒子的适应度定义如下：

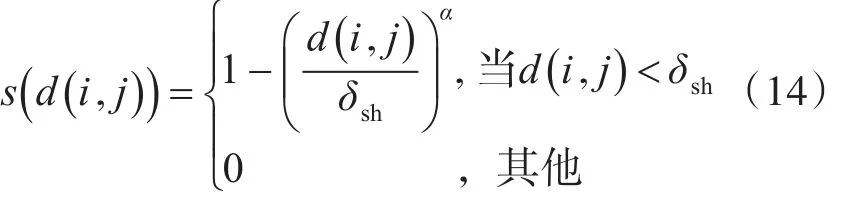
式（14）中：δsh为小生境半径，在计算时可预设为常数； α为常数，论文中置为2。

本算法采取轮盘赌的方法根据精英集中各个粒子的适应度选取全局最佳位置，在算法迭代过程中，具有全局最佳位置的粒子指导其他粒子按照式（11）～（12）更新各个粒子的位置和速度；每次迭代之后，选取所得粒子中的非劣解加入到精英集中，这样精英集中的粒子数会因迭代次数的增加而不断增加，从而影响算法的运行速度；因此，当精英集中的粒子数超过精英集的最大容量时，根据适应度式（13）计算精英集中各粒子的适应度，删除其中适应度较小的个体粒子。

当算法满足终止迭代条件时，精英集的粒子即可认为是所求的Pareto最优解。

4.3 模型求解步骤

应用改进的算法求解模型，步骤如下：

1）根据负荷总量和分布式电源总容量及各节点下容量约束条件，用向量X来表示DG的位置和容量信息，其中中，xi=0 表示不需要接入，xi≠0表示i节点接入xi数值大小容量的DG。初始粒子种群，规模N，速度υmax，精英集的容量M，M初始为空集，迭代次数t=0，Genmax，采用前推回代潮流计算方法对初始化的粒子进行各目标值的计算，并保存。

2）选取粒子群中的非劣解加入精英集中，利用式（13）计算精英集中各粒子的适应度。

3）未满足终止退出时，执行步骤4）至7），否则结束。

4）根据精英集中各个粒子的适应度选取全局最佳位置，按照式（11）～（12）更新各个粒子的位置和速度，再计算种群内各粒子的各目标函数值。

5）选取粒子群中的非劣解加入精英集中，利用式（13）计算精英集中各粒子的适应度，并且删除精英集中适应度小的劣解，保证精英集中的个体数不超过其最大容量。

6）如果当前粒子的位置优于其历史最佳位置的粒子，则用当前的粒子替换，如果当前粒子的位置既不优于也不劣于其历史最佳位置的粒子，则按照50%的概率替换或保持，对于劣于Xipb的粒子，按照5%的几率进行变异操作，即再次初始化该粒子。

7）如果群体中某个粒子当前的位置优于全体粒子的历史最佳位置，则更新，否则保持全体粒子的历史最佳位置不变。

8）最后所得的精英集即为所求的Pareto最优解集。本算法在求解过程中加入限制条件（如步骤中的Vmax，精英集的容量M），在步骤6）中改善了变异机制。

5 算例分析

5.1 DG接入配电网对静态电压稳定性的影响

为研究分析分布式电源接入系统的位置和容量对电网电压稳定性的影响，以IEEE33节点系统为例，设置如表1的方案。其中方案一是通过改变12节点的接入容量来研究分布式电源的容量对电网电压稳定性的影响；方案二、三、四是通过改变分布式电源接入系统的位置来研究分布式电源接入位置对电网电压稳定性的影响。方案中假定分布式电源都采用P-Q（V）型的。由Matlab仿真得到图2～5的曲线图。

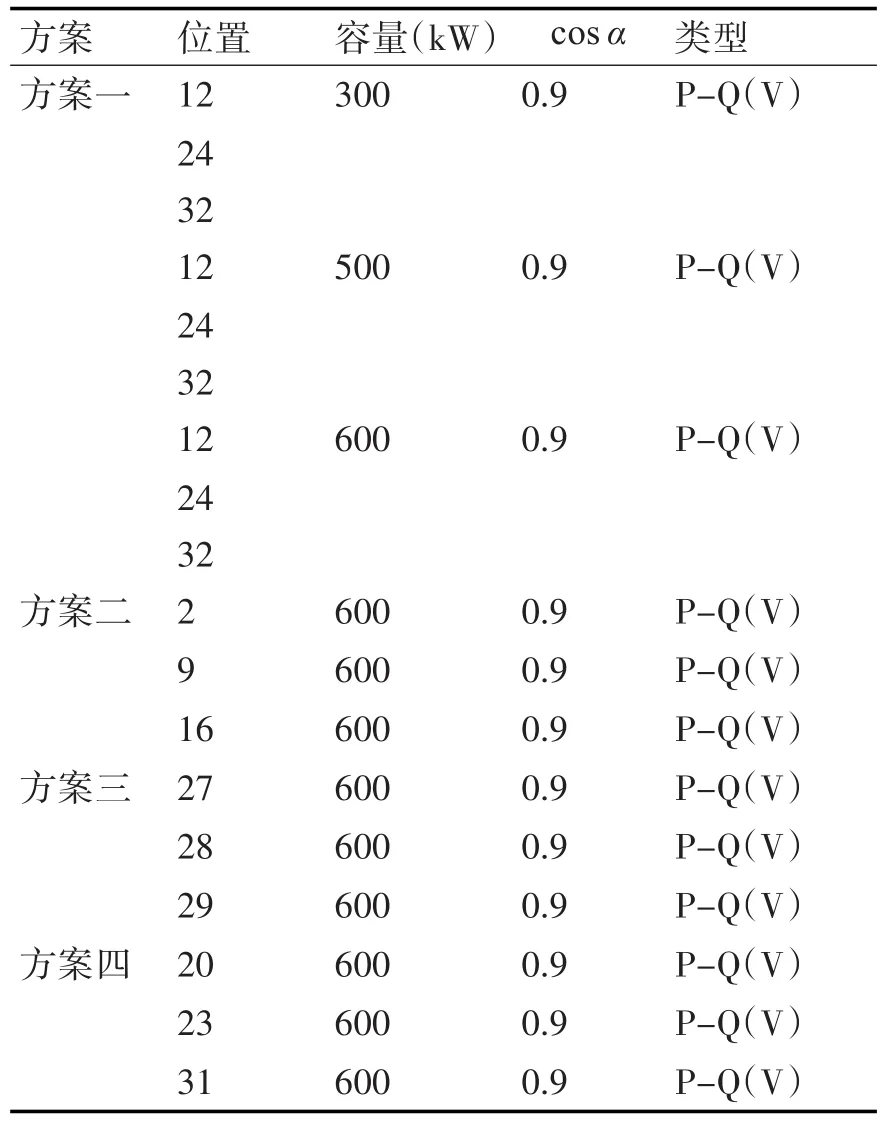
表1 P-Q（V）型分布式电源接入配电网方案设置

从图2、3、4、5的仿真结果可以发现并得到结论：在相同节点接入不同大小的P-Q（V）型DG，电网中各节点的电压提升量跟接入容量的大小成正比关系，在一定范围内接入容量越大，电压提升量越大，越有利于系统的稳定运行；在主馈线上接入P-Q（V）型DG，靠近末端接入对电压的提升量大于靠近电源首端接入对电压的提升量；在同一引出馈线上接入P-Q（V）型分布式电源，靠近引出末端接入对电压的提升量大于靠近引出馈线首端接入对电压的提升量；在靠近电源端的引出馈线上接入P-Q（V）型分布式电源对电压的提升量大于远离电源首端引出馈线上接入对电压的提升量。

图2 方案一下的节点静态电压稳定指标L

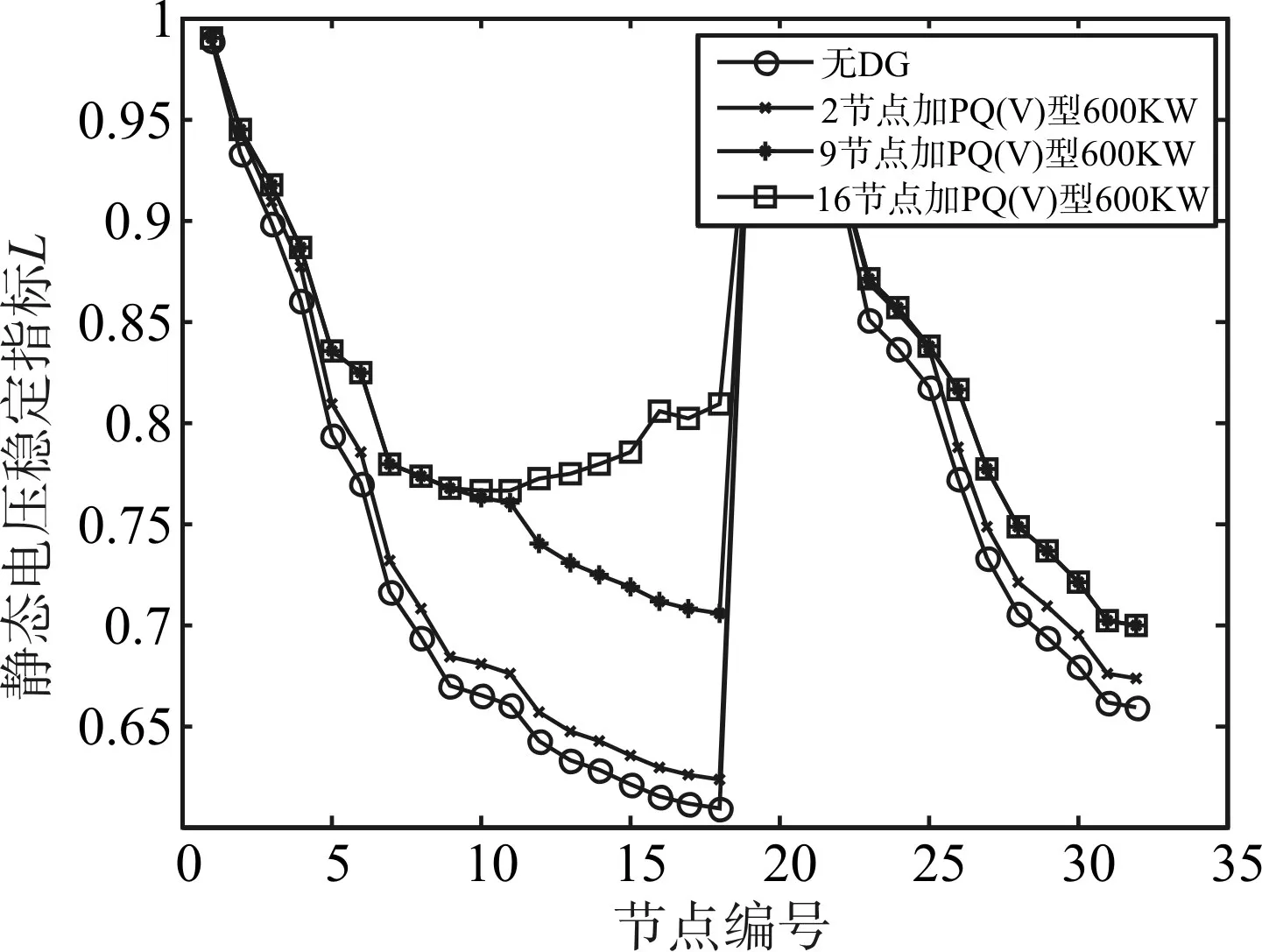
图3 方案二下的节点静态电压稳定指标L

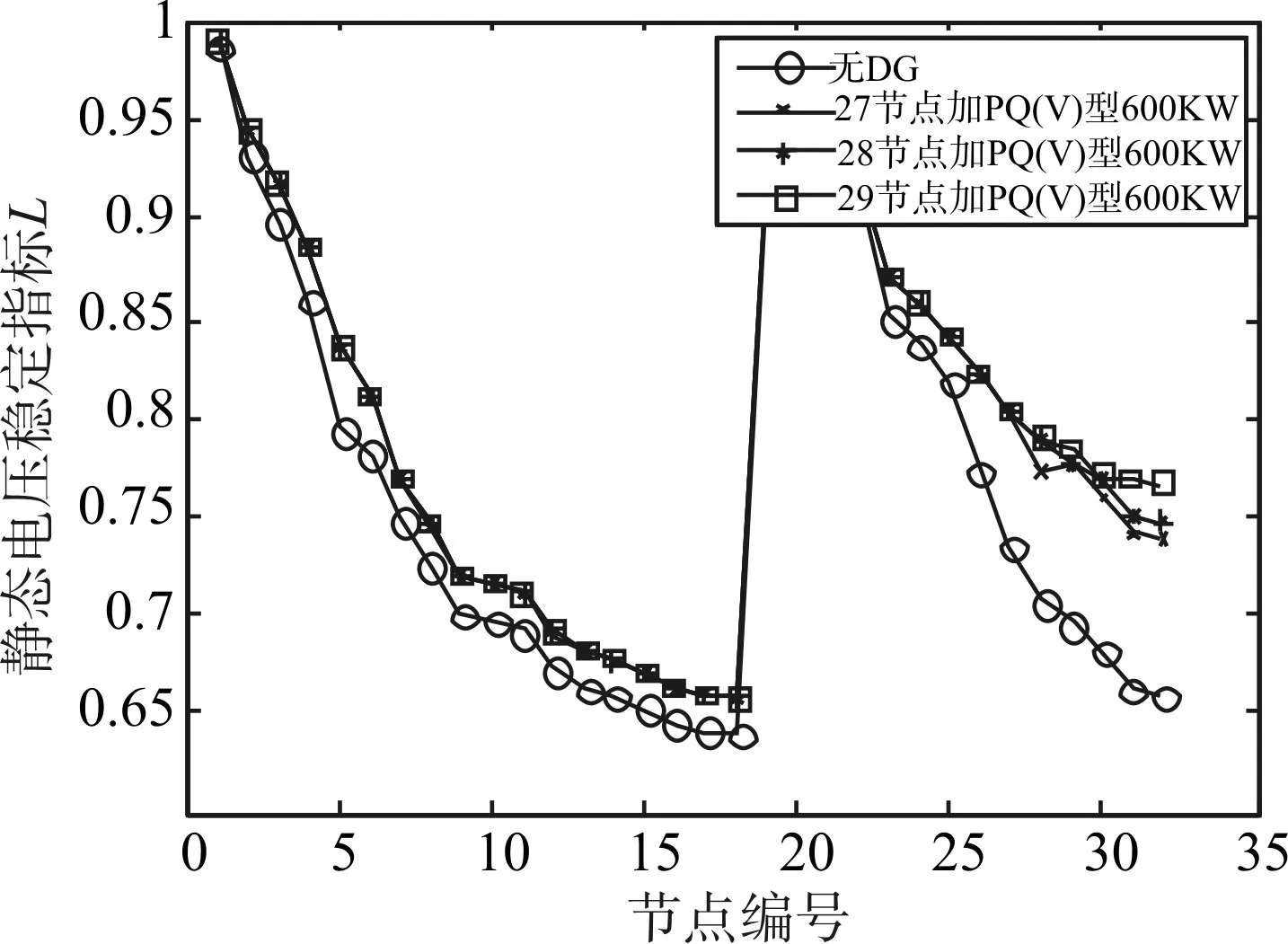
图4 方案三下的节点静态电压稳定指标L

图5 方案四下的节点静态电压稳定指标L

5.2 选址定容仿真分析

以美国PG&E69节点配电系统为算例，系统结构如图6所示，基准电压12.66kV，系统总负荷3802.19kW+2694.6kvar。假设网络中允许接入分布式电源的节点为节点2～节点69。分布式电源的总装机容量不得超过380 kW，分布式电源的功率因数为 0.9。ω=0.75，c1=c2=1.495，δsh=0.48，α=2，种群规模为90，Genmax=50。

对分布式电源多目标优化配置模型进行求解，得到的最优解集如图7所示。

图6 69节点测试系统

图7 Pareto最优解集

图7 反映了DG投资与运行成本之和与网损、电压稳定裕度之间存在相互制约的关系。DG的投资与运行成本较小时，网损和电压稳定裕度较大；而配电网网损和电压稳定裕度较小时，分布式电源投资经济性又无法达到用户满意的要求。相对于加权单目标优化而言，得到的各目标函数值和决策指标值直接明了，能够兼顾多个指标，在一次计算中得到满足各种需要的解，给决策者提供了足够的选择空间，有效地提高了优化决策水平。

表2给出了从最优解集中选出的三组典型解，当决策者追求投资与运行成本最小时，方案一是最好的选择；当决策者追求配电网网损和电压稳定裕度最小时，方案三是最好的选择；方案二对应的三个目标函数都不是最优的，但是方案的总体满意度较好，能够协调好三个目标函数之间的关系。

表2 算法典型解

6 结语

文中首先构建了静态电压稳定指标，为研究分布式电源接入位置和容量对配电网安全稳定运行的影响，设置了不同的方案进行仿真，仿真结果证明了DG容量和接入位置对配网有重要影响，同时有效验证了模型的有效性。然后，为减少DG的容量和位置不合理规划造成的不利影响，文中建立了以综合成本、网损和电压稳定裕度为目标函数的模型，采用了一种小生境多目标粒子群优化算法对模型进行求解。通过算例仿真，求解了多目标Pareto解。在实际决策过程中，规划人员可根据不同偏好或实际需求从Pareto最优解集中选择合适的最优解，实现DG的多目标最优选址定容，为分布式电源的经济可靠接入配电网提供重要的指导意义。