基于MapReduce的人工蜂群算法在大数据中的应用*

李 果 袁小凯 许爱东 张乾坤 张福铮

（南方电网科学研究院 广州 510080）

1 引言

当前，可采集数据规模不断增大，在短时间内已很难通过人工分析的方式从中得到有价值的信息。数据挖掘技术作为目前十分流行的数据分析技术，常被用于发现数据中潜在的某种模式，从而为作出最优的决策提供依据［1～2］。

聚类一种重要的数据挖掘技术，主要用于将某个集合中的项分配到目标类别或簇，使得同一簇中成员的相似性最高，而不同簇中的成员相似度较低。近年来，仿生算法如遗传算法（GA）、差分进化（DE）、蚁群优化（ACO）、离子群优化（PSO）等被用于解决聚类问题［3～4］。Maulik［2］等提出了被称为“GA-聚类”的基于遗传算法的聚类方法，该方法从特征空间搜索到适当的簇中心，来优化利用相似性度量得到的簇。王勇臻等针对K-means算法依赖于初始聚类中心和易陷入局部最优解的缺陷，提出一种改进的求解聚类问题的差分进化算法［5］。单冬红等对通过使用不同的作业集群调度算法运行相同的作业，进行横向对比，得到各种作业调度算法之间在计算能力、运行时间、资源占用等方面的优劣，对收敛速度方面和易陷入局部最优问题进行了改进，提高了聚类速度和效果［6］。Cura等利用微粒群优化方法，通过模拟鸟类结队和鱼的群居行为特征来解决聚类问题［7］。然而，大规模数据集通常包含相当多信息量的大量文件，上述序列聚类算法在对大规模数据进行聚类时，往往在内存空间和计算时间等方面具有较大开销［8］。目前，MapReduce编程范式已经成为另一个数据并行编程模型，可将计算任务自动并行处理，且具有较好的容错和负载均衡能力，受到了众多研究者的青睐［9～10］。研究人员基于MapReduce，提出了多种利用分布式计算方式对大规模数据进行聚类的方法。王焱将K-means和蝙蝠算法结合应用在云计算虚拟机智能调度上，降低了物理节点数量和提高资源利用率［11］。文献［12］提出了并行K-PSO方法，提高了传统方法的聚类效果和处理冗余数据的能力。为解决PSO算法在对大量数据进行聚类时效率较低的问题，基于MapReduce并行方法，文献［13］提出了MR-CPSO算法。同时Anchalia和Roy等提出了基于MapReduce范式的K-近邻方法，来解决分布式计算环境下的大量数据的处理问题［14］。

针对大规模数据聚类问题，本文提出了基于MapReduce的人工蜂群聚类算法，能够对大规模数据进行高效聚类。

2 聚类和人工蜂群算法基本原理

2.1 聚类

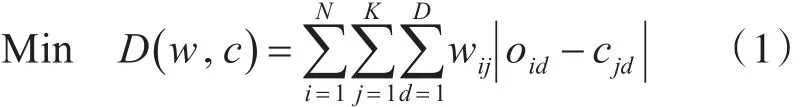
其中，wij表示对象oi在簇 j中的权重。 j个簇的中心记为可通过式（2）计算得到

其中，Nj为第 j个簇中对象的个数。

聚类问题可看作是寻找对象到簇的最优分配的过程。每个可能的分配方案即为一种可能的解决方法，簇内对象间相似度越高，分配方案越好。

2.2 人工蜂群算法

人工蜂群算法是一种元启发式算法，常见的主要步骤如下：

1）随机分布式初始化食物源的位置；

2）所有雇佣蜂选择一个候选食物源位置，基于之前已选择食物源位置的临近位置，选择新的食物源位置，若新的候选食物源位置适应度更高，则更新雇佣蜂记忆中原有的食物源位置，并返回蜂巢，与观察蜂共享新的食物源位置的适应度；

3）每个观察蜂根据从雇佣蜂得到的适应度值以一定概率选择新的食物源位置；

4）观察蜂前往被选择食物源的位置，并根据所选食物源，选择其临近的新的食物源位置；

5）丢弃所有适应度未增加的食物源位置，并由侦察蜂随机确定的新的位置。

上述过程重复执行，直到迭代次数达到最大循环次数。其中，步骤1）、步骤2）和步骤3）在重复过程中，于步骤5）之前循环执行。

3 基于MapReduce的人工蜂群聚类算法

3.1 算法流程和主要步骤

本文提出的基于MapReduce的人工蜂群算法的主要流程如图1所示，主要步骤如下：

1）随机分布式初始化食物源位置，并将其作为雇佣蜂的初始位置。初始位置用如式（3）表示：

其中，xi为以D维向量表示的食物源位置为目标函数，决定着当前位置的优劣，SN表示食物源的数量。

2）更新雇佣蜂新的中心值。将初始位置作为雇佣蜂的当前位置，并基于当前位置对邻域进行搜索。在搜索过程中选择新的位置，可通过式（4）计算得到

图1 基于MapReduce的人工蜂群聚类算法基本流程

其中，vij为基于与临近位置（xkj）随机选择位置的比较，对之前位置xij的修正位置。φij为[- 1，1] 内的随机值，用于在下一次迭代时，将之前位置随机调整为新的位置。为随机选择的索引。

3）基于MapReduce计算适应度。基于MapReduce计算雇佣蜂从邻域搜索到的新的食物源的适应度，如果该适应度高于原位置的适应度，则用该位置更新原有位置。

4）观察蜂从雇佣蜂选择中心值并更新。雇佣蜂返回蜂巢，并将新的食物源位置共享给观察蜂，观察蜂根据共享信息利用式（5）选择食物源位置：

其中，fiti表示食物源i的适应度，与食物源i的目标函数的值有关。选择食物源位置后，观察蜂前往该位置，并利用式（4）选择其邻域中心的食物源位置。

5）基于MapReduce计算新位置的适应度，并根据适应度的大小决定是否更新当前位置。

6）考察一段时间内中心值适应度是否增加，如适应度未增加，则丢弃当前中心值，则侦察蜂重新产生新的中心值，否则，执行步骤7）。

7）考察中心值是否满足条件，如是，则执行步骤8），如否，则执行步骤2）。

8）利用最优中心值对数据进行聚类。

在上述步骤中，由于对大规模数据，适应度的计算会耗费大量时间。因此，本文采用MapReduce来计算适应度的值。

3.2 基于MapReduce的适应度计算

基于MapReduce的适应度计算方法具体步骤包括：

1）映射函数从簇的中心开始，将数据记录到Hadoop分布式文件系统中；

当传感器测到铁丝导线时，由于导线的表面积较小，所产生的涡流很小，并且由单片机读取的LDC1000收集到的数据很小，当检测到硬币时，由于硬币的大表面积，产生的涡流很大，并且由单片机读取的LDC1000收集到的数据将比以前大得多。因此，我们可通过设定阈值来区分铁丝与硬币。

2）映射函数从每个蜜蜂提取中心值，计算数据记录与中心值之间的距离，并返回最小距离及其中心的编号。映射函数使用蜜蜂的ID和中心的ID来建立一个新的合成键，并根据最小距离计算新的值；

3）映射函数将新的键和值调用给规约函数，规约函数利用同一个键的多个值，计算得到平均距离；

4）规约函数调用键和平均距离，计算得到每个蜜蜂的适应度值。

4 实验

为了对提出的算法的性能进行评估和验证，本文从算法的聚类效果、扩展性和聚类效率3个方面开展了实验。

4.1 实验设置

本文算法和对比算法均以Perl语言实现，并在包含10个节点的Hadoop集群中运行，每个节点的配置为：1核2.26 GHz CPU，2G内存，120G硬盘空间，Ubuntu 14.04操作系统，Apache Hadoop 2.6.2。

算法中使用的数据集包括仿真数据和真实的磁盘驱动器制造数据（HDD）2个部分。其中，仿真数据为UCI机器学习数据集中的4个基准数据集，如表1所示。为了获得大规模的仿真数据，本文通过多次复制，将每个基准数据集扩充到约1000万条记录。磁盘驱动器制造数据包含了硬盘驱动器制造过程中的材料、工具和过程等特征，包括制造成功实例（1457000条记录）和制造失败实例（14300条记录），每个类别的数据均用30个特征表示，包括属性、参数等。

表1 4个测试数据集

4.2 实验结果

4.2.1 聚类效果测试

在衡量聚类效果时，本文采用F值度量（F-Measure）方法来评估聚类的准确度［15～16］。F值度量（F-Measure）方法将每个簇作为一个查询，将每个类别作为查询的预期结果。算法得到的簇j和已标记的基准数据中类别i之间的F度量值可利用式（6）计算得到

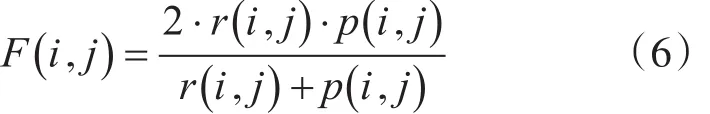
其中，r和p分别表示F值度量方法中的召回率和精度。召回率定义为，精度定义为其中，nij为存在于簇j的类别i中的成员的数量，ni和c分别为类别i和簇j的大小。大小为c的整个数据集的F度量值可通过式（7）计算得到

其中，F值的上限为1，当且仅当类别i中的全部实例被分到簇j时。F越大，表示聚类的效果越好。

基于仿真数据，本文实现了基于MapReduce的人工蜂群聚类算法，与现有的PK-Means算法［9］和并行K-PSO算法［10］的聚类效果比较结果如表2所示。其中，初始簇的中心是通过计算随机抽取0.1%的数据记录的平均值得到的。

表2 不同数据集的F度量值计算结果

从表2可以看出，本文算法的F度量值明显高于PK-Means算法和并行K-PSO算法的F度量值，即本文算法的聚类效果更优。

基于硬盘驱动器制造数据，本文与现有算法聚类效果的比较结果如图2所示。

图2 基于硬盘驱动器制造数据的聚类结果

从图2中可以看出，与PK-Means算法和Parallel KPSO算法相比，本文算法得到的结果的F度量值更高，比PK-Means算法聚类结果的F度量值提高了58%，因此，本文算法明显优于两种比较算法。

4.2.2 可扩展性验证

在并行计算中，可扩展性是指当增加负荷和处理器资源时，系统增加总吞吐量的能力，加速比是指并行算法比对应的串行算法增加的速度，加速比Sp可利用式（8）计算得到

其中T为单个节点的运行时间，TN为N个节点的运行时间。

为了验证本文算法的可扩展性强弱，分别在2的倍数个节点上执行算法，算法的运行时间和加速比测试结果如图3、4、5、6、7所示。

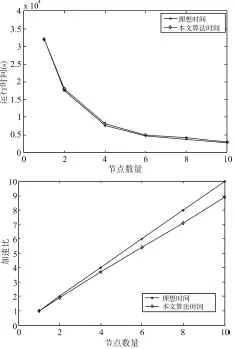
图3 基于数据集Ⅰ的运行时间和加速比

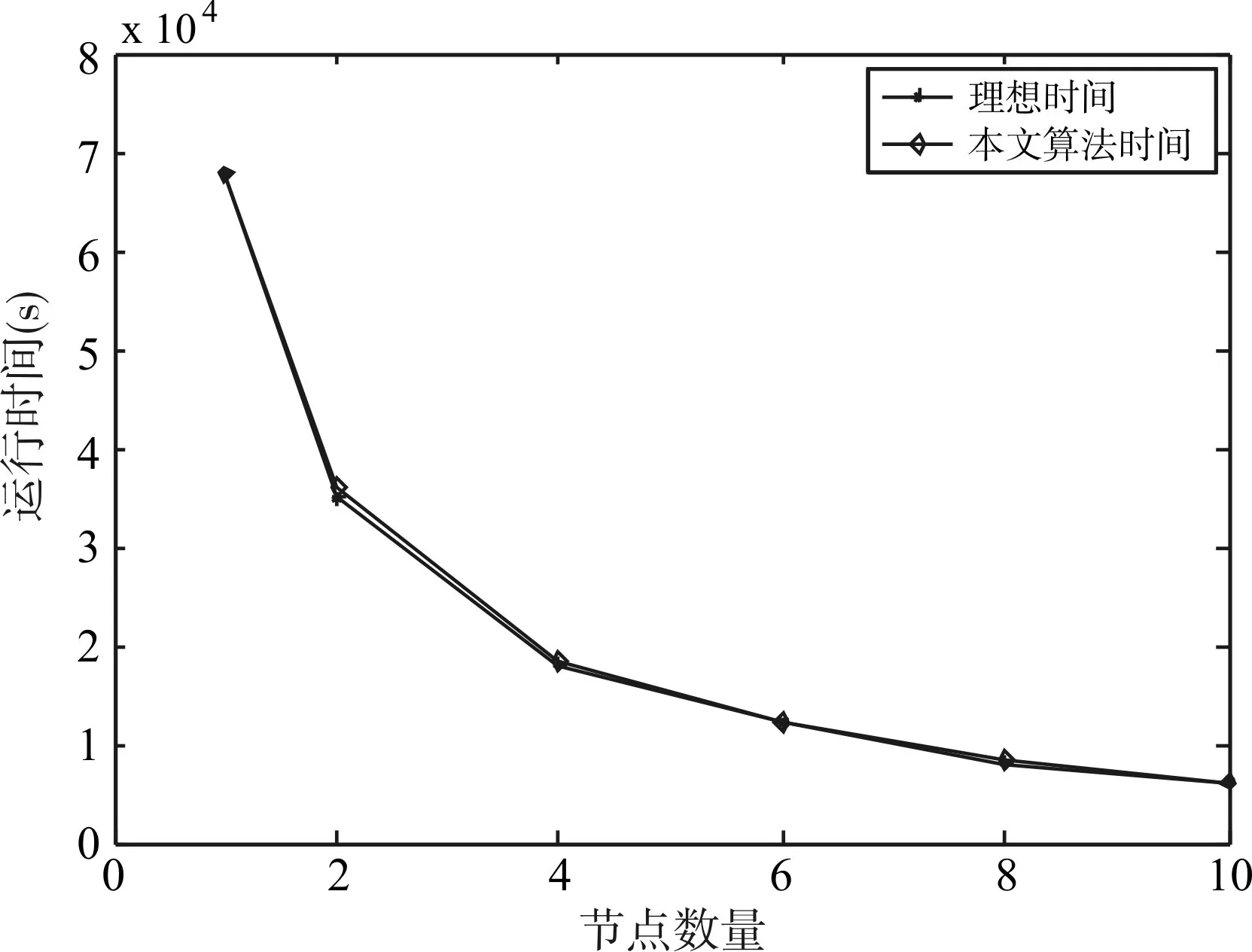
图4 基于数据集Ⅱ的运行时间和加速比

图5 基于数据集Ⅲ的运行时间和加速比

图6 基于数据集Ⅳ的运行时间和加速比

图7 基于数据集HDD的运行时间和加速比

从图3、4、5、6、7可以看出，本文算法的运行时间随着节点数量的增加迅速下降，加速比与理想加速比十分接近，因此，本文算法具有较高的可扩展性。

4.2.3 聚类效率测试

除对算法的聚类效果和可扩展性进行测试外，本文还测试了算法对大规模数据的聚类效率。在10个节点上对不同大小的数据集进行聚类，数据集的大小从2GB到10GB不等，测试结果如表3～表6所示。聚类效率可通过式（9）计算得到

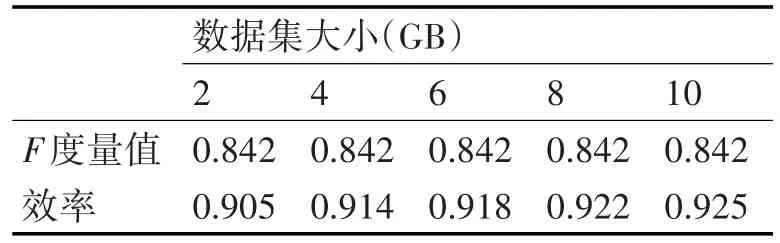
表3 基于数据集Ⅰ的F度量值和效率

表4 基于数据集Ⅱ的F度量值和效率

表5 基于数据集Ⅲ的F度量值和效率

表6 基于数据集Ⅳ的F度量值和效率

从表3～表6可以看出，随着数据集的增大，本文算法的性能逐步提高，效率达到90%以上。实验结果表明，对大规模数据进行聚类时，本文算法可节省大量时间，显著降低成本，能够在合理的时间内处理大规模数据，并保持较优的处理结果。

5 结语

本文针对大规模数据聚类问题，提出了基于MapReduce的人工蜂群聚类算法，并利用仿真数据和磁盘驱动器制造真实数据两类数据对算法的聚类效果、可扩展性和效率进行了验证，实验结果表明，与PK-Means算法和并行K-PSO算法相比，本文算法具有更好的分类性能。在以后的研究中，将在更大规模的数据集上开展实验。