一种改进的直觉模糊信息系统的决策规则及其约简*

夏秀云 田 浩 常安成 刘一龙

（1.湖南信息学院公共课部 长沙 410003）（2.湖南信息学院电子信息学院 长沙 410003）

1 引言

Fuzzy集的概念是由美国计算机与控制论专家L.A.Zadeh 提出的［1～3，12～15］，主要是研究有关模糊问题以及不确定性问题的理论方法，该理论主要强调集合边界的不分明性。直觉模糊集是模糊集的延伸，是保加利亚学者Atanassov于1986年提出的一种在对象与集合的关系中增加非隶属度和犹豫度等两方面信息的数学方法［4～6］，其表达不确定信息时比传统模糊集有更强的表达能力及灵活性。近年来，学者们进行了有关的多方面研究。比如：何迎东等学者［7］提出了直觉模糊集上的改进的四大运算法则；王艳平等学者［8］结合区间的特殊性，给出了区间值直觉模糊粗糙集；樊磊等学者［9］从模糊二元关系角度出发，提出一种基于直觉模糊集的知识获取方法；江红莉等学者［10］研究了基于直觉模糊理论的群决策判别方法；Huang等学者［11］从直觉模糊β邻域出发，提出了一种新的粗糙集模型；司小蒙［12］从覆盖集与直觉模糊集角度出发，提出了多粒度覆盖粗糙直觉模糊集模型。然而，基于直觉模糊集的知识发现的文献还比较少。基于此，本文提出了一种改进的直觉模糊信息系统的决策规则及约简方法。本文首先给出直觉模糊信息系统的预备知识，然后构造了一种改进的直觉模糊集并研究其性质及规则提取，最后通过实例验证方法的有效性和可行性，为直觉模糊信息系统进一步研究起铺垫作用。

2 预备知识

在实数集R中，记R+={x | x＞0，x∈R} ，R上的全体模糊集合记作F(R)。

定义 1［1～2］设∈ F(R )，且满足以下条件：

1）∃x0∈R，使得

则称A~为R上的模糊数。一般记R上的全体模糊数为F(R)。

定义2［4～6，14］设非空论域为 U ，X ⊆ U ，在 U 上有如下两个映射：

为U上的一个直觉模糊子集。其中uA~(x)表示为A~的隶属度，vA~(x)表示为A~的非隶属度。为了方便，U上的所有直觉模糊子集用IFS(U)表示。

定义 3［4～6，14］设 A~、B~分别是论域 U 上的直觉模糊子集，则A与B的并、交和补与定义如下，设

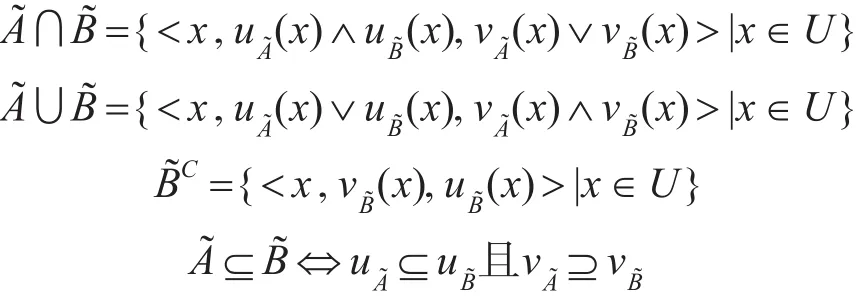
3 改进的直觉模糊集

定义 4［4～6，14］设直觉模糊信息系统为四元组，即IFIS=(U，A=C∪{d}，V，f)，其中 U 为论域；C 和{d}分别为条件属性集和决策属性集；为属性值的集合，Va为属性a的直觉模糊值域；f:V×A→V 为信息函数，即 ∀x∈U ，a∈A，有f(x，a)=＜ua(x)，va(x)＞∈A~（ A~为 U 上的直觉模糊集）。若C∩{d}≠∅，则称IFIS为直觉模糊决策系统。

定义 5［3，13］令 X∈IFS(U)，L={(m，n)|m+n≤1，0≤m，n≤1}，对于任意 (m，n)∈L ，则 Xnm={x∈U|uX(x)≥m，vX(x)≤n}为直觉模糊集 X的 m，n截集。当m=1，n=0，X1为直觉模糊集X的核。

定义6设U是一个非空论域，A~∈IFS(U)，x∈R，R为论域U的一个等价关系，定义x关于A~的直觉模糊粗糙隶属度、非隶属度分别为

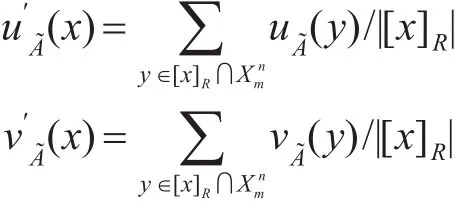
其中，|[x]R|为等价类的基数表示 x属于 A~的程度，表示x不属于A~的程度。

定义7（改进的直觉模糊集）设U为论域，R为U上的一个等价关系，A~∈IFS(U)，x∈U，令近似精度 0≤β1＜1-β2＜0.5，定义 A~关于截集 (m，n)的上、下近似定义为

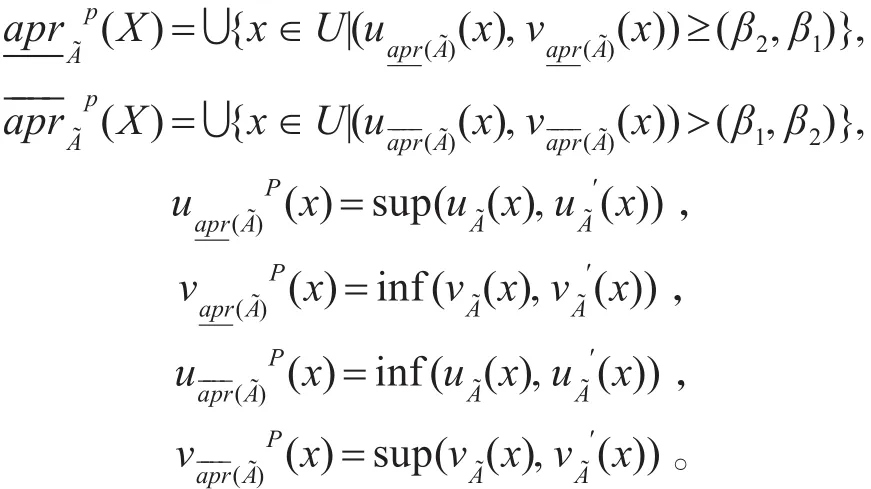
4 改进的直觉模糊集的性质及规则提取

定理 1 设 (U，R)为一近似空间，A~，B~∈IFS(U)，x∈U，P⊆C，取 0≤β1＜1-β2＜0.5，则改进的直觉模糊集可以得到如下的性质：

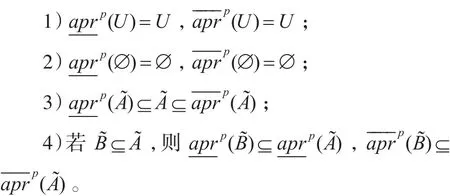
定义8 设 IFIS=(U，A~=C∪{d}，V，f)是一个直觉模糊信息系统，P⊆C为条件属性集，X⊆U，0≤β1＜1-β2＜0.5，则改进的直觉模糊集的近似依赖性为

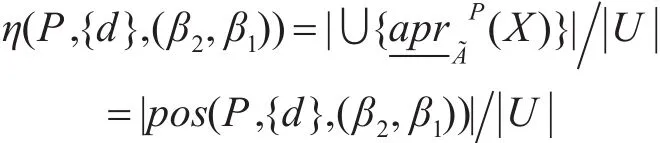
其中，η表示在改进的直觉模糊信息系统中可能正确分类的知识在已有知识中的百分比。

改进的直觉模糊集的近似约简redp(C，{d})定义为

的最小子集P⊆C，称为C关于｛d｝的一个约简。所有约简的交集称为核。

从上述讨论可知，引入 (β2，β1)后，获得改进的直觉模糊集决策系统的近似约简，可以导出相应的决策规则：

其中，Ci为条件类，Yj为决策类。接下来进行实例分析。

例1考虑表1给出的直觉模糊信息系统，表2给出的直觉模糊决策划分表。其中，条件属性C=｛C1，C2，C3｝，一个决策属性D=｛d｝。

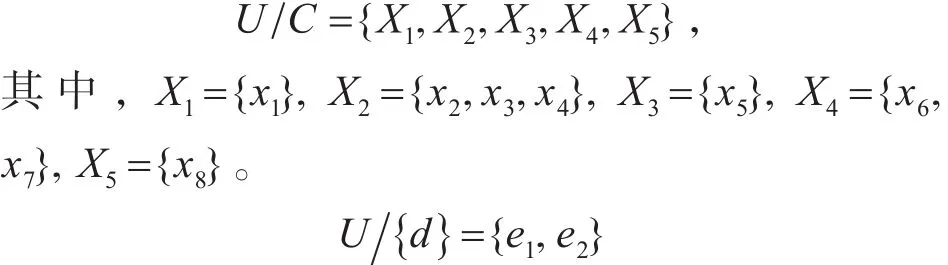
其中，e1={x1，x4，x5，x8}，e2={x2，x3，x6，x7} 。

解 ：令k=sup{u1(x)，…，ur(x)} ，f=inf{v1(x)，…，vr(x)}，其中k，f为决策类e1，e2隶属值最值，r分别为两类决策类包含的元素个数，故r=4。

其中，={x∈U|u(x)≥0.03，v(x)≤0.91}，计算e1类的粗糙隶属函数得：

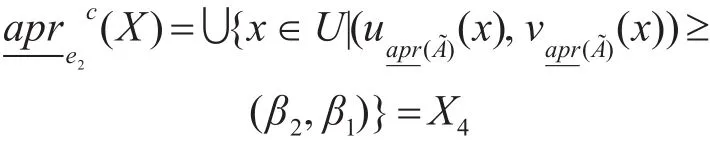
从而可得直觉模糊集的近似依赖性为

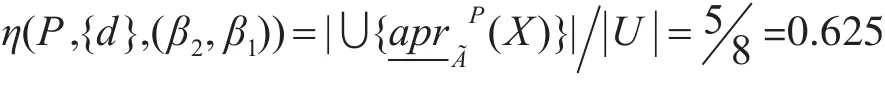
对C1，C2，C3分别计算η(P，{d}，(β2，β1))，则最后可以求得一个 (β2，β1)的约简为（C1，C3）。从而得到改进的直觉模糊信息系统的决策规则：

以上规则的支持数分别是2、2，对应的置信区间分别是（0.94 ，0.01），（0.86，0.12）。

通过以上实例分析，本文给出的方法是有效可行的，易实现。只需要知道信息系统中的决策类、条件类，便可以计算时间复杂度。故本文提出的方法有效促进了改进的直觉模糊信息系统在决策问题中的应用，为后续粗糙直觉模糊集的构建及在三支决策方面起到很好铺垫作用。

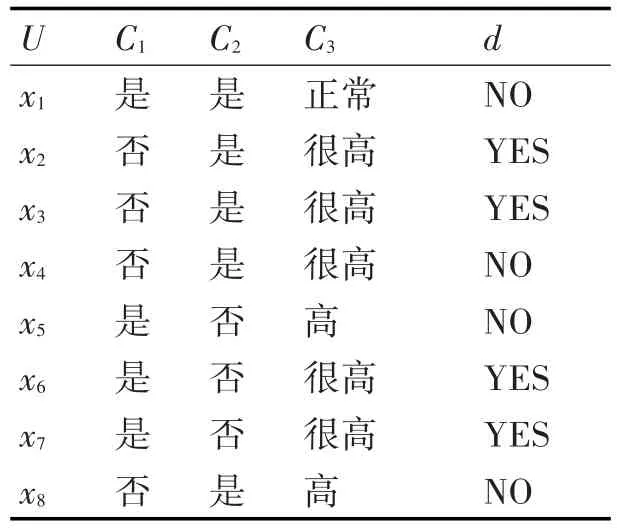
表1 直觉模糊决策表

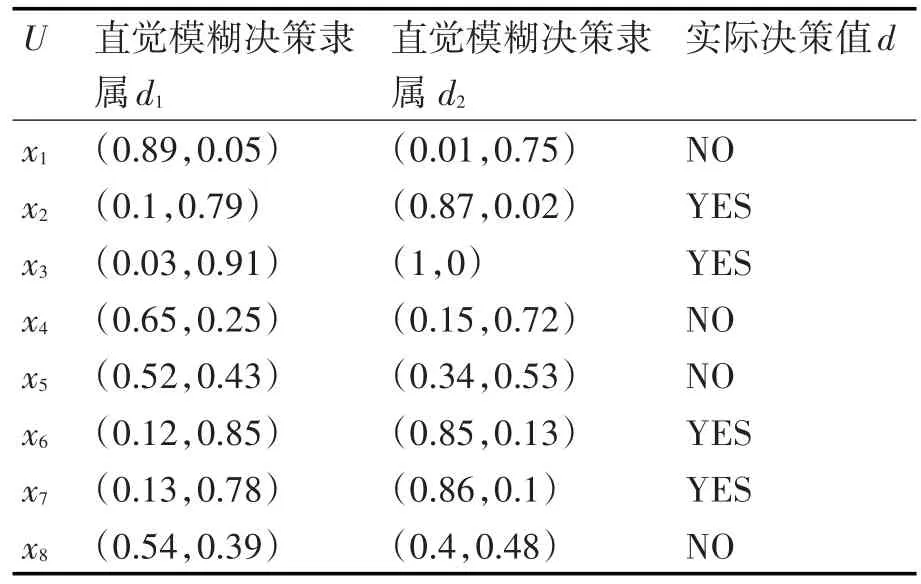
表2 直觉模糊决策类的划分表

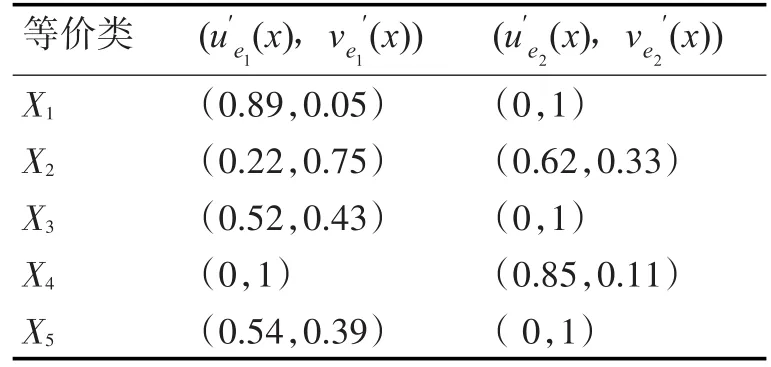
表3 决策类的粗糙隶属函数值

5 结语

本文借助截集，定义了直觉模糊粗糙隶属度和非隶属度，构建了一种改进的直觉模糊集模型，并讨论了粗糙直觉模糊的决策规则和方法，为直觉模糊信息系统的其他模型（如：三支决策模型）研究提供一种理论参考。